轻型车传动轴总成的主要零部件静力有限元分析
2015-12-24尹长城马迅杨强
尹长城,马迅,杨强
(湖北汽车工业学院汽车工程学院,湖北十堰442002)
轻型车传动轴总成的主要零部件静力有限元分析
尹长城,马迅,杨强
(湖北汽车工业学院汽车工程学院,湖北十堰442002)
建立了十字轴、轴管、花键轴的有限元模型,通过线性静力计算得到其应力和变形,并进行强度校核,同时利用理论解验证有限元模型的正确。在此基础上,对轴管进行弹塑性分析,得到极限扭矩。
有限元;十字轴;花键轴;轴管
传动轴是汽车传动系统的主要部件,在汽车行驶过程中起着传递运动及动力的作用。传动轴结构承受主要是扭矩,其强度和刚度校核是传动轴静力设计的主要部分。通过有限元计算传动轴结构的应力和变形是一种准确、快捷的方法。本文中建立传动轴结构主要零部件的有限元模型,包括十字轴、轴管、花键轴;并进行材料力学公式理论验证;然后对轴管进行弹塑性分析,得到极限扭矩。
1 十字轴静力分析
材料为20MnVB,其弹性模量为210GPa,泊松比为0.3。采用10节点四面体和20节点六面体混合分网,大部分为六面体单元,网格尺寸3mm,其中节点数31367、单元数9320,如图1所示。
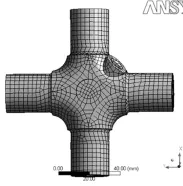
图1 十字轴网格划分
由运动形式可知,万向节叉的内孔壁和十字轴轴颈承受大小相等、方向相反的扭矩,将其转化为垂直于接触面的力。本文中轻型车的发动机最大扭矩T为240 N·m,变速箱一挡的变速比ik1为6.143,传动效率90%,计算传动轴承受最大力矩[1]:

假设力作用于十字轴轴端轴承的中间位置,如图2所示,r为44mm,该力大小为


图2 十字轴受力
该力作用面沿圆周方向(180°)是余弦分布[2],在Ansys-Workbench软件加载可利用轴承载荷模拟其受力。十字轴上下的轴颈圆柱面(一半)施加轴承载荷,在左右轴颈圆柱面(一半)施加固定约束。经过静力计算,得到十字轴的应力和位移分布。最大Mises应力为360.3MPa,发生在轴颈的根部,如图3 a所示。材料20 MnVB的屈服极限为885MPa,安全系数为
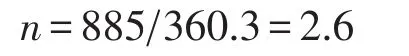
本传动轴总成的十字轴设计安全系数要求大于2,满足设计要求。十字轴上下轴颈端部产生最大变形,其值为0.0885mm,如图3b所示。图4为距合力P作用点为15mm的Mises应力图,其中t为15mm时最大应力为168.7MPa。

图3 十字轴Mises应力及变形云图

图4 t为15 mm时的截面Mises应力云图
将轴颈简化成悬臂梁,利用材料力学理论,应力根部最大,变形最大发生在自由端处,且截面处应力是外侧最大,中间(中性轴)最小。有限元计算与材料力学理论定性吻合。
利用材料力学公式[3]进行应力定量验证:
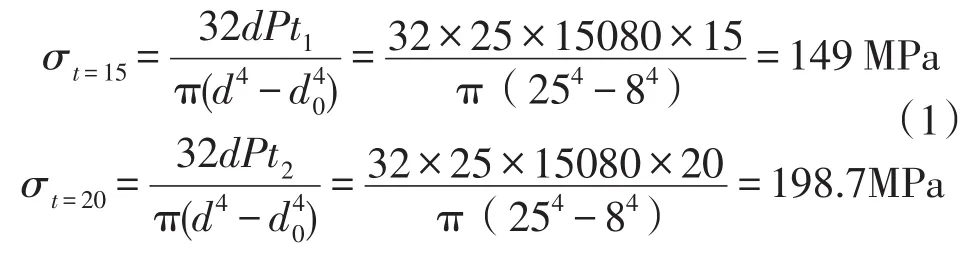
此处忽略弯曲切应力影响,即材料力学计算的弯曲正应力与Mises应力相等。t为15 mm时截面理论估算解与有限元的数值解相对误差为

根部(t=20 mm)应力理论估算解与有限元解相差较大,这是因为在轴颈根部存在应力集中,式(1)计算得到的应力结果为名义应力,若存在应力集中,真实应力计算如式(2)所示:

式中:Kt为应力集中系数,根据应力应变手册[4]计算应力集中系数的公式为
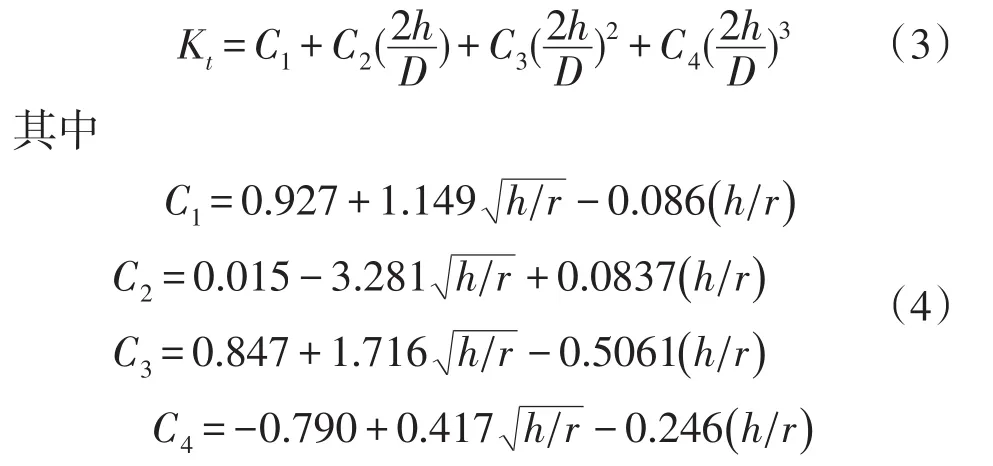
式中:r为根部的圆角半径;D为轴颈的外径;h为2个轴颈的半径之差。针对十字轴模型得
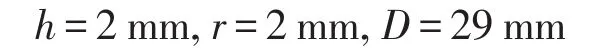
代入式(3)~(4)得应力集中系数Kt为1.693,由式(2)计算最大应力为336.4MPa,与有限元计算结果的相对误差为

理论解与数值解存在一定的误差,因为基于材料力学的力学模型是一维梁理论,有限元则是依据三维弹性理论。有限元法针对模型和受力都更符合十字轴的真实情况。且十字轴采用高阶单元仿真,其结果较理论估算解精确,但理论解较好地验证了有限元模型的正确性。
2 轴管和花键轴静力分析
轴管和花键轴的材料为40Cr,其弹性模量为210GPa,泊松比为0.3,屈服极限为800MPa。设计安全系数要求大于1.5。轴管采用4节点壳单元,网格尺寸4 mm,节点数35148个,单元数35032个。花键轴采用10节点四面体和20节点六面体分网,大多数为六面体网格,网格尺寸为4mm,节点数72778个,单元数21914个,如图5所示。对轴管和花键轴的端面施加扭矩,另端施加固定约束,扭矩大小为1327N·m。

图5 花键轴网格划分
花键轴最大Mises应力为627.5MPa,发生在加载端部。这是应力奇异的体现,因左端作用扭矩,整个凹槽段的应力分布应较为均匀。凹槽段末端发生最大Mises应力,其值为443.3MPa,如图6a所示。计算其安全系数为

符合设计要求。花键轴实心轴段受纯剪切,其最大切应力为199.8MPa,如图6b所示。花键轴最大周向位移0.336 mm,如图6 c所示。该值除以半径16.25mm得扭转角为0.021rad。
利用材料力学扭转公式[3]计算最大切应力和扭转角为
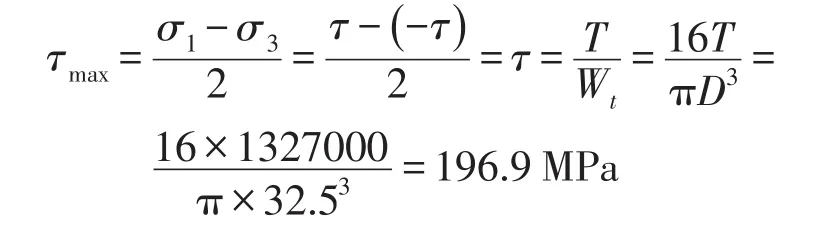

图6 花键轴应力及位移云图

理论解与有限元数值解很接近。验证有限元模型是正确的。
传动轴轴管为空心圆管,长度l为604 mm,外径D为76 mm,厚度t为2.5mm。有限元计算结果与理论解的对比见表1。有限元解与理论解比较接近,有限元计算的安全系数为
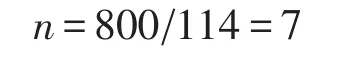
符合设计要求。
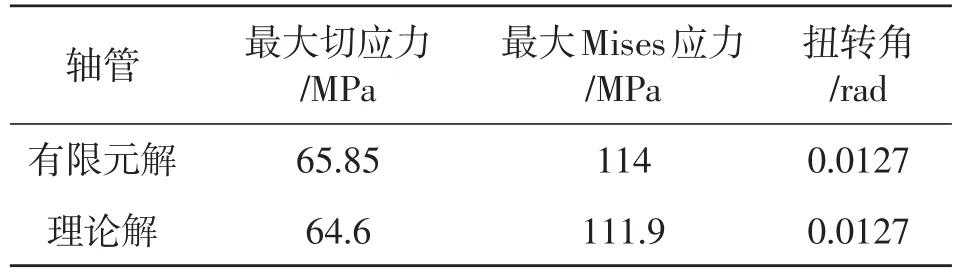
表1 轴管有限元解与理论解对比
3 轴管极限扭矩计算
利用Ansys确定轴管极限扭矩的大致范围,给结构施加一个稍大的载荷,打开自动荷载步二分法,并进行弹塑性非线性静力分析,最后计算会因不收敛终止,则倒数第2个子步对应的就是轴管的极限扭矩[5]。绘制扭矩扭转角曲线至极限载荷时,应呈水平线。轴管采用理想弹塑性模型,理论计算极限扭矩[6]为

施加扭矩大小为10000 N·m,分成30个子步加载,经过计算后,模型在26个子步时不收敛。读取25子步结果,如图7所示,轴管已经全部屈服,TIME为1对应扭矩为10000,TIME为0.978101对应扭矩值为极限载荷9781 N·m。选择一个节点(8716号),查看轴管的周向位移,位移值除以半径,得到扭转角,绘制其载荷位移曲线,得到曲线如图8所示,从曲线上可以看出扭转角随着扭矩的增大而增大,最后随着扭转角的增大所需要的扭矩不再改变。有限元确定的极限扭矩与理论解相差较小,证明弹塑性模型正确和确定极限扭矩的方法可行。

图7 确定轴管极限扭矩

图8 轴管载荷位移曲线
4 结论
1)轻型车传动轴总成的十字轴、轴管、花键轴线弹性有限元分析结果表明满足设计要求。
2)线弹性和弹塑性的理论计算验证传动轴结构各零件的有限元模型正确。
3)利用有限元法可较为准确地确定结构的极限载荷。
[1]王望予.汽车设计[M].4版.北京:机械工业出版社,2011.
[2]刘涛,杨长征.基于Nastran的十字轴万向节有限元分析[J].郑州轻工业学院学报:自然科学版,2009,(2):98-101.
[3]刘鸿文.材料力学.[M].5版.北京:高等教育出版社,2011.
[4]W.C.Yong.Roark’s Formulas for Stress and Strain[M].New York:McGraw-Hill,1989.
[5]朱邦俊,王玉华.运用有限元方法确定T型管节点的极限载荷[J].应用力学学报,1988(4):47-54+135.
[6]余同希.塑性力学[M].北京:高等教育出版社,1989.
Finite Element Static Analysis on Major Parts for Light Vehicle Drive Shaft Assembly
Yin Changcheng,Ma Xun,Yang Qiang
(School of Automotive Engineering,Hubei University of Automotive Technology,Shiyan 442002,China)
The finite element model of joint cross,spline axis,shaft tube was built.The stress and deformation were obtained through linear static calculation,and the strength was checked.The finite element model was verified by theory resolution.On this basis,the elastoplastic stress analysis on the shaft tube was conducted,and the ultimate torque was got.
finite element;joint cross;spline axis;shaft tube
U463.2;TH122
A
1008-5483(2015)01-0013-04
10.3969/j.issn.1008-5483.2015.01.004
2014-11-05
湖北省重点实验室开放基金(ZDK201104)
尹长城(1976-),男,吉林大安人,硕士,从事汽车结构有限元分析研究。E-mail:71267753@qq.com
