k／n（t）：（G）系统与时间相关的容量n（t）

刘春霞，何 平

（西南交通大学 数学学院，四川 成都610031）

0 引 言

为提高系统可靠性常采用冗余的方式，而冗余并非万能，虽然能提高系统可靠性，但大量备用件会导致系统负荷过重、体积过大或者资源消耗过多等问题。目前，很多文献提及如何配置冗余以达到效果最优［1－5］，同时也有文献提及一些高要求设备上，并不使用冗余来提高系统可靠性。

k／n： （G）系统作为一种冗余系统，同样存在上述问题，该系统的研究也为国内外可靠性数学领域的热门内容。目前k／n：（G）系统的可靠性计算是可靠性领域的一个NP难题，因此对该系统的研究存在很多方面的困扰，特别是涉及该系统的维修问题。文献 ［6］建立了随机载荷作用下失效相关的动态可靠性模型，对k／n 系统可靠度和失效率随时间的变化规律进行了研究；文献 ［7］基于部件寿命服从指数分布的基础上对表决系统可靠度进行了分析；文献［8］利用Monte carlo随机抽样技术，对系统可靠性评估指标进行了模拟计算；文献 ［9，10］对k／n：（G）系统的维修策略进行了部分研究，但由于大容量表决系统的可靠性计算困难，大量的研究都基于系统小容量或者基于部件寿命服从指数分布的假设下，对由消耗型部件组成的k／n：（G）系统的可靠性以及选择何种容量的k／n： （G）系统甚至该情况下的维修策略研究较少。

基于上述背景，本文考虑一种由消耗型部件组成的表决系统，在系统最小工作数k 固定的情况下，根据系统期望的运行时间，对系统与时间相关的容量进行了分析。在此基础上，考虑让k／n： （G）系统以逐步增加部件的方式运行，严格推导了该方式下系统可靠性的计算公式，设计迭代算法，解决系统可靠性计算的难点。对比一次性选定的系统与逐步增加部件的系统部件使用量大小，得出逐步增加部件的方法平均每1～2天增加一个部件，时间间隔够长，且能够明显减少部件的投入使用量，从而节约大量资源。

1 预备知识

1.1 符号说明

k／n（t）：（G）系统表示由n（t）中取k系统，其中n（t）视情而定；

n（t）表示k／n（t）：（G）系统t时刻的系统容量；

Pt为可靠性阈值，当系统可靠性大于阈值则系统工作，否则失效。

1.2 k／n：（G）系统

k／n：（G）系统是指一个具有n个部件组成的系统，当n个部件中有k 个或者k 以上的部件工作，系统则正常工作，否则系统失效。其中n为系统容量，k为系统工作的最小工作部件数。k／n：（G）系统的可靠性框架如图1所示。

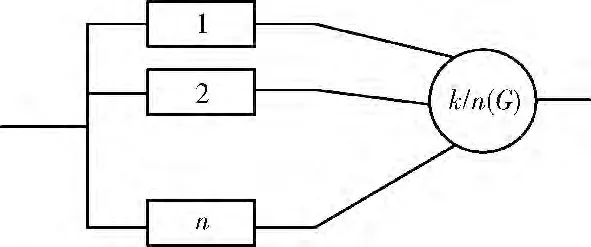
图1 k／n：（G）系统

若k／n：（G）系统中的n 个部件独立同分布于F（t），且记初始时刻部件为新，则系统的可靠度R（t）与时间的关系为

式 （1）显示了当k 固定时，在同一时刻t，系统的可靠性会随着系统容量的增加而增加。

2 k／n（t）：（G）系统系统容量n（t）的选择

在系统工作要求的条件下，可以根据期望的运行时间，选择某种容量的k／n（t）：（G）系统。很明显，如果对系统期望的运行时间不长，系统容量就会很小，反之很大。如果根据对系统期望的运行时间而事先选择某种容量的k／n（t）：（G）系统，由于部件一开始全部投入使用，部件热备冗余导致部件寿命过早衰减，浪费了资源以及部件的可靠性，以这种方式选择系统容量理论上并不是最优选择。

2.1 k／n（t）：（G）系统根据系统期望的运行时间一次性选择n

一般而言，k／n（t）：（G）系统要求工作的最小部件数k是一定的，系统容量n（t）视情而定。系统可靠性随着时间的增加呈现递减的趋势。而实际上，当对系统要求较高时，不仅需要表决系统存在k 个或者k 个以上部件工作而且需要系统可靠性R（t）大于事先给定的阈值Pt。系统可靠性与时间以及阈值的关系如下

系统可靠性R（t）分别是关于时间的递减函数和系统容量的递增函数，式 （2）给出系统可靠性与系统容量随时间的关系。根据式 （2）逐一对不同容量系统可靠性的计算，可以确定在系统期望运行时间的要求下k／n（t）：（G）系统的最小容量n（t）。

2.2 k／n（t）：（G）系统以逐步增加部件的方式选择容量n

基于上述研究，考虑以逐步增加部件的方式运行k／n（t）：（G）系统，即先给定一个小容量n0（n0＞k）的k／n0：（G）系统，使系统开始运行，当系统可靠性下降到阈值Pt时，立即对系统增加一个新部件，系统可靠性升高，当系统可靠性再次下降到阈值Pt时，继续对系统增加一个新部件，……以此类推，根据上述过程的系统可靠性计算，可以确定在系统期望运行时间内，系统需要的最小容量以及逐步增加部件的时间序列。具体各阶段系统可靠性计算公式如下，给定容量n0的k／n0：（G）系统与时间相关的可靠性

依次类推，可以推导任意容量的系统的可靠性

式中：m——某正整数。通过迭代的算法，可以通过已知的信息，计算任意系统容量的可靠性如图2所示，其中箭头表示信息的传递方向。

图2 系统可靠性计算

3 算例研究

针对上述根据系统期望的运行时间一次性选定系统容量以及新提出方法的情况，有必要用数值算例验证两种情况优劣。

3.1 k／n（t）：（G）系统根据系统期望的运行时间一次性选择容量算例研究

设计者常常对系统关键部件或者其它部件配置冗余以保证系统可靠性。由于k／n（t）：（G）系统部件属热备冗余，能较好的保证系统可靠性，因此被生产部门常采用。对于选择何种容量的k／n（t）： （G）系统将成为一个优化决策的问题。

同样认为系统工作所需要的最小部件数k 是一定的，假定k＝50，且要求系统可靠性大于可靠性阈值pt＝0.75时系统才算工作。所有备选部件属同质部件且寿命Xo（以年记）同分布于W（1.2，0.01；t）。因此不同系统容量n的与时间相关的系统可靠性如图3所示。

图3 不同系统容量k／n：（G）系统的可靠性趋势

其中黑色点为系统在当前容量以及当前阈值下，系统工作与失效的时间分界点。在时间分界点以前系统工作，在分界点后系统失效，即在相应容量下，系统寿命为黑色点对应的时间。因此通过对系统期望的工作时间，可确定最佳的系统容量。不同容量系统可靠性随时间变化的平面趋势如图4所示。

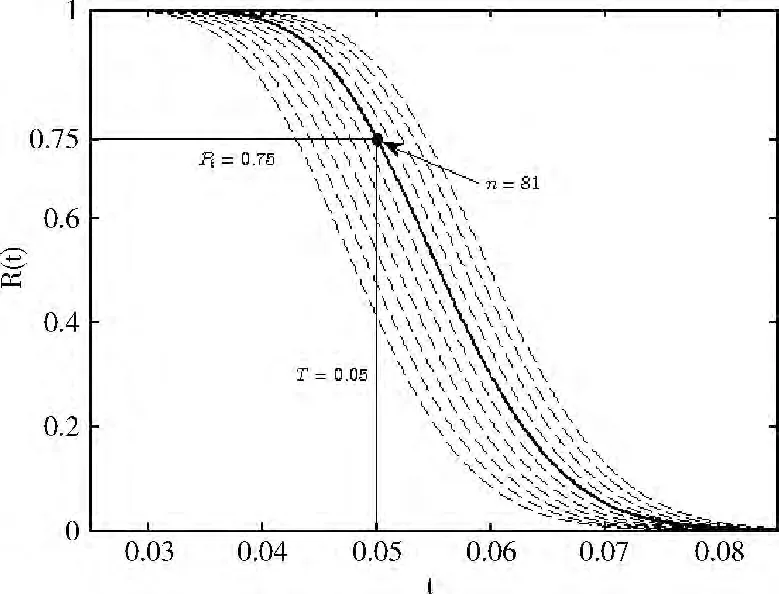
图4 不同容量系统可靠性随时间变化的平面趋势

其中黑色点表示在系统期望的运行时间T＝0.05 年，系统可靠性阈值pt＝0.75时，系统运行需要的最小容量为81。容量低于81的可靠性曲线，系统达不到期望的工作时间而失效，高于81的可靠性曲线，系统工作且可以继续工作，存在资源的剩余。因此对系统所期望工作的时间不同，系统容量的选择也不同，表1列举了对系统不同的期望工作时间下，系统最佳容量的选择情况。

表1 与时间相关的系统容量n（t）

3.2 k／n（t）：（G）系统以逐步增加部件的方式的容量选择算例研究

事实上，上述系统容量n（t）的选择并不一定是最优的，因此考虑对k／n（t）：（G）系统逐步增加部件，使系统冗余部件既存在热备冗余也存在冷备冗余，以此利用冷备冗余在备用过程中不消耗寿命的优势，节约系统投入使用的部件数量。

以3.1背景为例，选择初始容量n0＝60 （视情而定）使系统开始运行，当系统可靠性下降到阈值pt＝0.75时对系统增加一个新部件，以此类推，该过程下系统可靠性与时间的关系如图5实线所示。

图5 逐步增加部件的系统可靠性与时间关系

图5虚线表示原始系统在期望运行时间T ＝0.05 年下，系统最佳容量为81的可靠性曲线图。而实线表示系统逐渐增加部件的时间以及系统可靠性变化曲线，可以看出在同样期望工作时间下该系统只需使用67个部件，对比发现，逐步增加部件的方法能够明显的减少系统部件的投入使用量。且系统逐步增加部件的时间序列 （以年记）为（0.02139 0.02341 0.02507 0.02825 0.03276 0.03835 0.04477 0.05179），以天记的时间序列为（7.8073 8.5447 9.1506 10.3112 11.9574 13.9976 16.3411 18.9034），因此在期望系统工作的时间T ＝0.05年，即15天的情况下，平均每1～2天增加一个新部件并不算频繁。表2列举了该情形下系统最佳容量随系统不同的期望运行时间的选择情况。

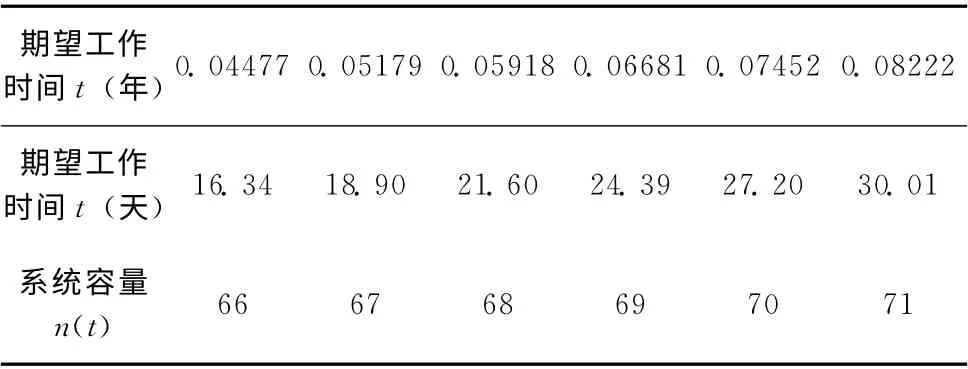
表2 与时间相关的系统容量n（t）

对比表1，表2系统最佳容量的选择，同样保证系统工作的条件下，以逐步增加部件的方式的表决系统可以明显减少系统部件的使用量。两种情况下系统不同期望时间以及对应的系统容量选择情况如图6所示。

图6 两种情况系统最佳容量选择对比

图6中线1、线2分别表示原始方法和提出方法两种情况下系统期望的运行时间与系统需要的最小容量的关系。可以看到线2在同样系统期望运行的时间下，系统需要的容量明显小于线1，即提出方法相对原方法有绝对的优势。

4 提出方法的优越性

首先，从理论上，提出方法 （k／n（t）： （G）系统逐步增加部件的方法）由于消耗性部件并没有全部一开始就投入使用，因此节约了大量消耗型部件的寿命，在劳动力资本相对部件使用资本足够小的情况下，提出方法理论上优于原方法。其次，从上述算例模拟研究的结果可以看出新方法具有明显的优势。虽然在算法上复杂于原方法，但是通过设计的可靠性计算流程，可以解决算法上的难题，且算法耗时可以很短，因此在实践上提出方法也优于原方法。对k／n（t）：（G）系统，调整系统使用的最小部件参数k 或者调整部件的参数，均可以通过调整代码而算出结果，并且得出的结论是一致的。

5 结束语

本文研究最少部件工作数k固定情况下，k／n：（G）系统的最佳系统容量n（t）随时间的选择。在系统期望工作时间内，列举了部分一次性选定的表决系统的最佳系统容量n（t）以及逐步对表决系统增加部件所选择的最佳系统容量n（t）。并在相同的系统工作时间内，对比了两种方式所选择的系统容量，结果显示在长时间工作的情况下，逐步对表决系统增加部件的方式可以减小部件的使用量，且逐步安装部件的时间间隔较长，并没有频繁的增加部件导致劳动量较大，但不可排除逐步增加单个部件的方式会存在个别时间间隔较短，同时增加两个或者更多可能更优，但这种情况下，增加不同个数部件会导致系统可靠性计算的困难，因此后续的研究中将考虑个别增加两个及以上的情况，并进一步考虑该情况系统可靠性的计算的方法。

［1］CAO Jinhua，CHENG Kan.Reliability mathematical introduction ［M］.Beijing：Higher Education Press，2012 （in Chinese）.［曹晋华，程侃.可靠性数学引论 ［M］.北京：高等教育出版社，2012.］

［2］BAO Lei，LI Qingmin，YANG Pinglv.An inventory control model of redundant spare parts for surface ships［J］.Journal of Naval University of Engineering，2012，24 （5）：32－34 （in Chinese）.［包磊，李庆民，杨平律.带冗余度的航舰随行备件库存优化模型［J］.海军工程大学学报，2012，24 （5）：32－34.］

［3］DU Baojun.The redundant components allocation of continuous k－out－of－n system ［J］.Journal of Lanzhou Jiaotong University，2012，31 （6）：147－153 （in Chinese）. ［杜宝军.连续n中取k系统中冗余元件的分配问题 ［J］.兰州交通大学学报，2012，31 （6）：147－153.］

［4］XUE Tao，FENG Yunwen，QIN Qiang.The repairable spare components optimization of K／N cold standby redundant system considering scrapped ［J］.Journal of South China University of Technology，2014，42 （1）：41－46 （in Chinese）. ［薛陶，冯蕴雯，秦强.考虑报废的K／N 冷备份冗余系统可修复备件优化 ［J］.华南理工大学学报，2014，42 （1）：41－46.］

［5］Tipwimol Sooktip，Naruemon Wattanapongsakom，David W Coit，et al.Multi－objective optimization for k－out－of－n redundancy allocation problem ［C］／／International Conference on Quality，Reliability，Risk，Maintenance，and Safety Engineering，2012：1050－1054.

［6］WANG Zheng，XIE Liyang.Dynamic reliability model of kout－of－n system with dependent failur［J］.Chinese Journal of Mechanical Engineering，2008，44 （6）：72－78 （in Chinese）.［王正，谢里阳.考虑失效相关的k／n 系统动态可靠性模型［J］.机械工程学报，2008，44 （6）：72－78.］

［7］WANG Yongnian.Reliability evaluation of k／n［G］system［J］.Electronics Quality，2009 （10）：37－44 （in Chinese）.［王永年.n中取k 表决系统的可靠性评估 ［J］.电子质量，2009 （10）：37－44.］

［8］CHEN Yanqiao，JIN Jiashan.A simulation algorithm for reliability index of repairable K／N （G）system ［J］.Computer simulation，2008，25 （11）：115－118 （in Chinese）. ［陈砚桥，金家善.可修K／N （G）系统可靠性指标的仿真算法研究［J］.计算机仿真，2008，25 （11）：115－118.］

［9］ZHANG Dingzhou，BAO Lei，QIAN Cunhua.Reliability and maintenance policy of hierarchical voting system subjected to common cause failure［C］／／Reliability Operation Research Society of China Branch of the 8th Conference on Reliability，2009：170－178 （in Chinese）.［张鼎周，包雷，钱存华.基于共因失效的层次表决系统可靠性分析与维护策略［C］／／中国运筹学会可靠性分会第八届可靠性学术会议，2009：170－178.］

［10］ZHANG Tao，ZHANG Jianjun，GUO Bo.The analysis of（m，N＿G）maintenance strategy of the K／N system based on operational availability ［J］.Journal of Astronautics，2009，30 （1）：395－401 （in Chinese）. ［张涛，张建军，郭波.基于使用可用度的k／N 系统 （m，N＿G）维修策略分析 ［J］.宇航学报，2009，30 （1）：395－401.］