基于CPN的WBANs调度算法研究*

樊文豪，谢志军,2，俞文彬

（1 . 宁波大学信息科学与工程学院，浙江 宁波 315211；2. 维多利亚大学科学与工程学院，澳大利亚 墨尔本 14428）

基于CPN的WBANs调度算法研究*

樊文豪1，谢志军1,2，俞文彬1

（1 . 宁波大学信息科学与工程学院，浙江 宁波 315211；2. 维多利亚大学科学与工程学院，澳大利亚 墨尔本 14428）

将无线体域网间调度问题（Inter-WBANs Scheduling，IWS）转化为基于中央处理节点（Central Process Node，CPN）的调度，模型化为图着色问题。提出一种启发式混合遗传模拟退火算法对相应的WBAN进行调度，缓解网间干扰，使无线体域网的整体性能得到优化。另外， 本文基于仿真结果对算法进行了评估，实验结果表明该算法可以在动态WBAN干扰环境下更好地适用于功耗和资源受限的WBAN。

无线体域网 体域网间调度 图着色 混合遗传

1 引言

无线体域网（WBAN）是一种无线个人传感网，主要由1组无线传感器节点及1个中央处理节点（CPN）组成，具体如图1所示。其中CPN主要负责收集来自WSNs的重要数据。与传统无线传感网（WSN）不同，WBAN用户的移动使得对应网络具有较高的移动性[1]，网络拓扑结构和WSN相比也不够稳定。多个WBAN的动态拓扑结构与MANETs相似，但是WBAN是基于组而不是基于节点的动态拓扑。当区域中多个WBAN共存时，各个网络之间相互冲突的可能性极大，因此WBAN间调度研究就显得极为重要。

无线体域网的分布式冲突避免调度可以模型化为已知的分布式图着色问题（常用于W S N、M A N E Ts[2]）。相应的网络拓扑对应于图模型G=(V,E)。其中V表示传感器节点，E表示相互干扰的2个节点之间无线资源的冲突，颜色集C表示不同的资源单元（时隙、频带或者编码序列）。图G的顶点完全k着色对应()V GC→，其中|C|=k。这样相邻节点所获得的颜色不同，相应的邻接点获得的资源不同，避免网络之间的冲突。

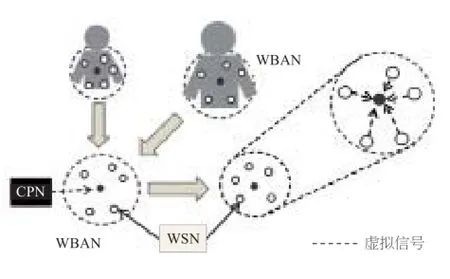
图1 WBAN网络模型

本文通过将WBANs调度模型化为图着色，提出一种启发式混合模拟退火遗传算法。该算法克服了遗传算法易陷入局部最优、模拟退火算法收敛较慢等缺点，以解决无线体域网调度问题。

2 基于CPN的WBAN调度模型分析

根据WBAN简单星型网络结构[3]中CPN/WSN的不对等关系，我们将WBAN调度模型简化为对WBAN中CPN节点的调度。单个WBAN中，CPN作为主节点，其他WSNs为其附属节点，CPN对WSNs的加入、离开以及资源分配进行管理。基于此，本文假设了1种基于CPN的2步IWS，具体如图2所示：

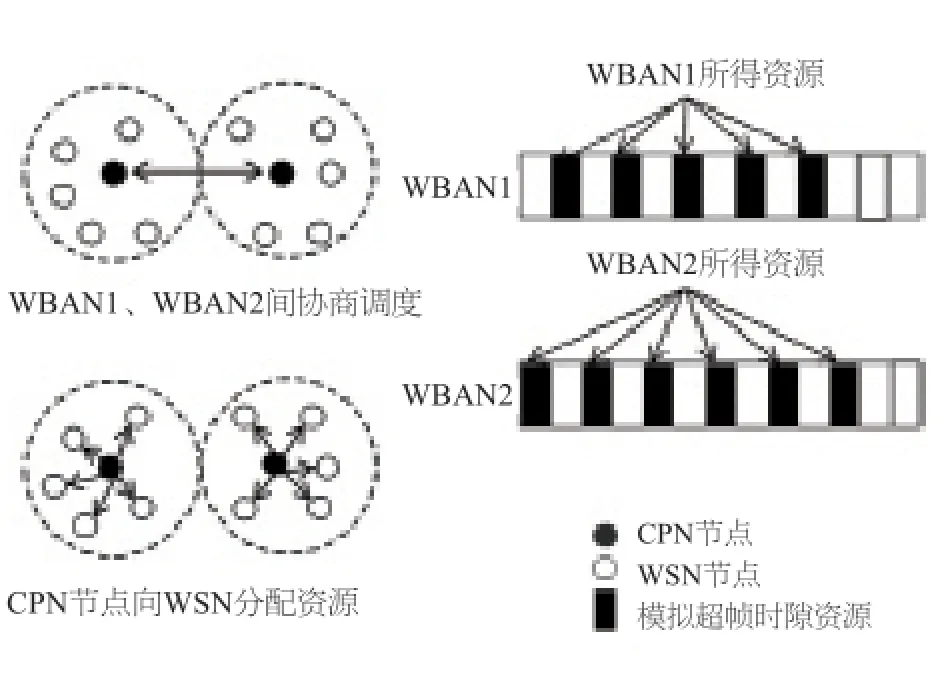
图2 基于CPN的WBAN调度模型

CPN首先与干扰范围内的其他CPNs进行资源协商，然后将占有资源向其WSNs进行分配。这样，当从对应的CPN接收到带有预先设定的传输模式的信标信息并遵循该模式向CPN发送重要信号时，WSNs被唤醒。

为模拟WBANs网络，随机构造1个2维图G=(V,E)。V(G)表示CPN集，E(G)表示CPN之间冲突链集。在一个区域内随机布置n=|V(G)|个顶点，用来模拟WBAN用户所处的随机空间位置。如果CPNs之间的距离等于或略小于WBAN之间的相互干扰范围，用边连接对应顶点。在这种情况下，基于CPN的IWS与MANET调度类似，但是两者对资源的调度策略不同。MANET中，每个顶点代表1个无线节点，MANET注重有效的内节点通信与路由。因此可以采用边着色，对应于节点与节点之间的通信调度，而在基于CPN的IWS中，每个顶点代表1个传感器组。基于CPN的IWS试图解决属于不同用户的传感器组之间的冲突问题。因此顶点着色对应于动态基于CPN的传感器组调度问题是合适的。这样基于CPN的IWS，1个随机图的k着色[4]可以对应于V( G)→C，其中|C|=k，邻接顶点就获得完全不同的颜色，相应地表示相关数据传输的不同资源单元（从WSNs到CPN）。着色算法执行1次，完成1次k种资源映射。

3 启发式模拟退火遗传算法解决图着色问题

简单的模拟退火遗传算法[5]结合了全局寻优与局部寻优性能，相对于单独的模拟退火算法或者遗传算法，其计算效率较高。因此在模拟退火遗传算法基础上添加启发式搜索，更有助于算法性能的提高。

3.1 启发式搜索算法

作为启发式算法的一种，贪婪算法采用贪婪准则逐步构造最优解。即在问题求解的每一个阶段，作出在一定标准下可能的最优决策。就图的顶点k着色来说，贪婪算法在进行着色时，会受限于染色体中顶点的次序，只能根据当前已经被着色的顶点和将被着色顶点的邻接信息来决定本着色顶点的颜色，而不能从全局出发，利用顶点间的关系构造最优着色。本文试图在已获得“次优解”的邻域内搜索1个“更好的次优解”，不断进行邻域搜索直到找到“局部最优解”。

3.2 启发式混合模拟退火遗传算法

在贪婪启发式遗传算法的框架下增加模拟退火算子，结合3种算法思想的优点，提出新的混合模拟退火遗传算法。

3.2.1 模拟退火算子设计

根据模拟退火算法思想[6]，本文设计的模拟退火算子如下所示：

1 输入：初始解S0，邻接矩阵A

2 输出：优化解S1

3 Begin

4 t=tf×Evaluation(S0)×tp；//计算初始温度t

5 Do

6 Do

7 n=Neighbor(S0)×Sf；//重新计算搜索次数

8 随机从S0的邻域中选择一个染色体作为S1

9 Δ=Evaluation(S0)-Evaluation(S1)

10 if(Δ＜0)

11 Then S0=S1；

13 While(循环次数＜n)

14 t=α×t；//α为降温系数

15 While(不满足终止条件)

16 Return S0；

17 End //其中tf、tp、Sf、α为用户自定义参数，控制冷却调度

另外，算法在每次遗传算法结束获得子代个体后，立即对子代个体执行模拟退火算子。其目的是：

1）在全体可行解空间的子集内进行搜索，以期望获得比原来更好的优化解。

2）与GGA（贪婪遗传算法）中只允许解质量的提高不同，必要时也允许解质量下降。以一定概率接受恶化解，扩大搜索范围，以期望能够跳过局部最优陷阱，尽可能克服早熟与欺骗现象。

3.2.2 启发式遗传算法

（1）建立染色体子空间

对于简单图G(n)，顶点集V(G)={v1,v2,…vn}，边集E(G)={e1,e2,…en}。邻接矩阵A(G)=(aij)n×n，矩阵A取值如下（n为G中顶点数）：

用C(k)={1,2,…k}来表示颜色集，即用k种颜色进行顶点着色。根据图着色以及遗传算法原理，染色体采用整数编码，具体如下：染色体由长度为n的序列x1x2…xn表示，xi(1≤i≤n)表示图中顶点vi所着颜色，xi∈C(k)。根据染色体子空间的定义，k种颜色对图G(n)着色，染色体子空间（即所有可能的着色方案）大小将达到kn，算法效率受到很大影响。为提高算法执行速度，将染色体的随机编码方案改为启发式着色染色体基因。

（2）适应度函数设计

执行启发式算法顶点着色时，为获取最优着色方案，需要得到最佳着色数。由此，适应度函数设计如下：

令wi(1≤i≤n)值恒为1，此时cmax即表示染色体序列中的最大颜色值。

（3）遗传算子设计

1）选择

选择算子采用简单轮盘赌策略[7]，即染色体的适应值越大，被选中的概率就越大。规模为n的种群中，染色体i的适应度值为fi，选择概率为pi：

2）交叉

染色体子空间设计过程中，由于采用整数编码方式，为避免产生非法染色体（不包含所有顶点或包含有重复顶点），交叉算子采用部分匹配交叉法[8]（PMX）。具体过程如下：

Begin

1 随机产生两个交叉点，并定义两点之间的区域为匹配区域

2 交换两个染色体的匹配区域

3 确定匹配区域间映射关系

4 染色体合法化

End

3）变异

变异算子采用简单换位变异[9]。过程如下：

Begin

1 染色体的两个基因位

2 将这两个基因位上的基因值进行交换

End

4）收敛性分析

定义：若P{M.C(x)=y}＞0，那么称作y通过x遗传可达。其中M.C(x)表示单个染色体x通过交叉和变异产生的个体。P{.}表示随机事件{.}的概率。

引理：若一个遗传算法满足如下2个条件：

a）对可行域中任意2个个体x和y，通过遗传是可达的；

b）种群序列P(0),P(1),…P(t),…是单调的。

定理：算法以概率1收敛到全局最优解（全局收敛性）。

证明：

x通过选择算子被选择的概率为Pc＞0。设c是由x通过交叉产生的任一子代染色体，z是由局部搜索产生的新子代，z参与变异的概率为Pm＞0，那么经过交叉变异由x产生y的概率满足：

设z=(z1z2…zn)，y=(y1y2…yn)，由变异算子可知，从xi产生yi的概率为（其中δ为已求得的k顶点着色方案中所用的最少颜色数）。

因此y由x通过遗传是可达的。

由算法的选择策略可知，P(0),P(1),…P(t),…具备单调性。综合以上2点可知遗传算法以概率1收敛到全局最优。

（4）启发式混合模拟退火遗传算法

启发式混合模拟退火遗传算法描述如下：初始产化种群N（包含n个染色体序列）。对种群N中的每个染色体进行贪婪着色（调用coloring）[11]，得到n个相应的着色序列，并对种群进行评价。若当前尚不满足终止条件，遗传算子作用于N，再次执行贪婪着色，并进行适应度函数评价。模拟退火算子作用于新种群，产生优质子代种群，再次执行贪婪着色，进行适应度函数评价，直至满足终止条件。具体描述如下：

1输入：图G，邻接矩阵A

2输出：最优着色序列

3Begin

4 i=0；

5 种群P(i)初始化；

6 种群P(i)中的每一染色体，调用coloring过程；

7 评价种群P(i)；

8 While(终止条件不满足)

9 遗传算子作用于种群P(i)产生子代种群C(i)；

10 模拟退火算子分别作用于子代种群C(i)中个体，

11产生优化的子代种群P(i+1)；

12 种群P(i+1)中每个染色体，调用coloring过程

13 评价种群P(i+1)；

14 i=i+1；

15 End While

16End

Coloring过程描述如下：

1 Coloring

2 输入：染色体y1y2…yn

3 输出：已着色染色体x1x2…xn

4 Begin

5 For(k=1 to n)

6 Call nextcolor(k)；//顶点着色

7 End For

8 End

nextcolor过程描述如下：

1 输入：等位基因yk，邻接矩阵A

2 输出：着色xk

3 Begin

4 k=0；

5 xk=0;

6 While(k＜n)

7 xk=xk+1；//从最小颜色值开始试探

8 i=0；

9 While(i＜n)

10 if(aij=1) and (xk=xi)

11 Then xk=xk+1，i=0；

12 End if

13 i=i+1；

14 End While

15 k=k+1；

16 End While

17 End

通过试验发现，引入启发式搜索和提高局部搜索能力的模拟退火算子之后，启发式混合模拟退火遗传算法在图着色问题中的寻优能力[10]有了很大提高，能够获取较好的最优解。

4 算法模拟仿真与实验结果对比

为验证算法性能，采用不同顶点密度的二维随机图对算法性能进行评估。根据第2部分中的系统模型，选用10个经典图集分别用来模拟空间WBAN低密度、中密度、高密度以及超高密度分布的情况，相互干扰距离设为2m。为保证算法对比的公平性，将不同算法在同样的参数环境下，对选用的图集分别进行10次试验，结果分别采用列表与仿真图进行对比。

启发式混合遗传模拟退火算法与传统遗传[12]算法试验结果对比如表1所示。其中，n表示图集中顶点数，m为边数，N表示种群规模，其中δ为已求得的k顶点着色方案中所用的最少颜色数，C表示当前算法求得的最优解，Tavg表示10次运行中求得最优解所用的平均进化代数。

表1 GA与HHGSAA同等条件下的实验结果数据对比

从表1中的数据可以看出，对10个标准图集，HHGSAA（混合遗传模拟退火算法）均找到了最优解。随着顶点数、边数的增加，算法求得最优解所需的进化代数也不断增加。对于高密度（Myciel5、Queen_8-8）及超高密度（Myciel6、Myciel7、Queen_9-9），HHGSAA也可以在不到50代的进化过程中获得问题的最优解。

图3、图4分别比较了算法GA和HHGSAA应用到图集Myciel以及Queen时所用的平均时间（算法GA与HHGSAA分别运行100次，计算平均寻优时间）。

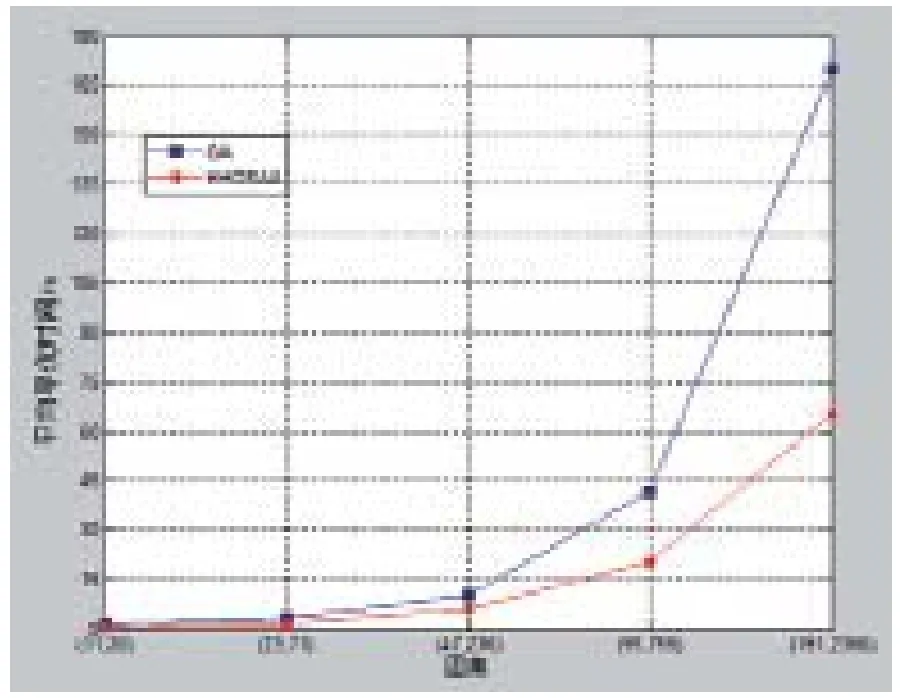
图3 GA与HHGSAA算法性能比较（Myciel图集）

除此之外，本文还对3种不同算法寻优结果中采用的平均最佳着色数进行比较。图5、图6分别为3种算法对Myciel图集和Queen图集的试验结果。

图4 GA与HHGSAA算法性能比较（Queen图集）

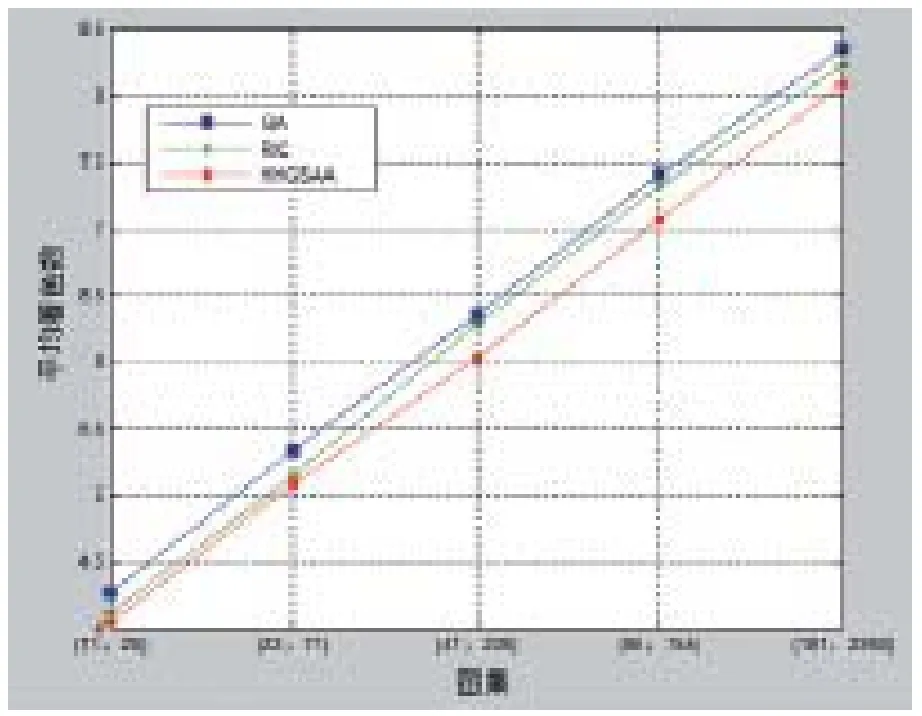
图5 GA、RIC、HHGSAA寻优结果（Myciel图集）

图6 GA、RIC、HHGSAA寻优结果（Queen图集）

由实验结果可以看出，HHGSAA与传统遗传算法以及RIC相比，在寻优能力和运行速度上都有相当大的提高。由此可见，HHGSAA在解决着色问题上有较大的潜力。

5 结束语

本文提出了一种启发式混合遗传模拟退火算法，实现了快速收敛、有效的WBAN间调度。与传统的完全着色模式不同，HHGSAA算法具备以下特性：

（1）采用启发式搜索方式，优化初始种群，以减少寻优时间。

（2）通过遗传与模拟退火这2种算法性能互补，加快算法寻优时间的同时提高解质量。

试验结果表明，HHGSAA算法克服了WBAN之间的冲突，从而提高了移动无线体域网的系统吞吐量。

本文着重于多用户随机场合，即可以模型化为2D随机图。在以后的工作中，将进一步分析算法在其他特殊场景中的性能。比如排队中的用户、影院里的用户、咖啡厅中的用户。这些场景可以分别模型化为线型、网格、簇图，以此评估其实时性能，并与已存在的WBAN解决方案（比如IEEE 802.15.4、蓝牙网络）进行比较。

[1] M Chen, S Gonzalez, A Vasilakos, et al. Body Area Networks: A Survey[J]. Mobile Networks and Applications, 2011,16(2): 171-193.

[2] S Gandham, M Dawande, R Prakash. Link Scheduling in Wireless Sensor Networks: Distributed Edge-Coloring Revisited[J]. Journal of Parallel and Distributed Computing, 2008,68(8): 1122-1134.

[3] S Cheng, C Huang. Colo ring-Based Inter-WBAN Scheduling for Mobile Wireless Body Area Networks[J]. IEEE Transactions on Parallel and Distributed System, 2013,24(2): 250-259.

[4] K Kothapalli, C Scheideler, M Onus, et al. Dist ributed coloring in O/spl tilde/(/spl radic/(log n)) bit rounds[J]. Parallel and Distributed Processing Symposium, 2006: 10-10.

[5] Eiben A E, Vender Hauw J K, Van Hemert J I. Graph Coloring with Adaptive Evolutionary Algorithms[J] . Journal of Heuristics, 1996,4(1): 16-24.

[6] D A Fotakis, S D Likothanassis, S K Stefanakos.

An E volutionary Annealing Approach to Graph Coloring[J]. Applications of Evolutionary Computing, 2001: 120-129.

[7] B L Miller, D E Goldberg. Genetic algorithms, selection schemes, and the varying effects of noise[J]. Evolutionary Computation, 1996,4(2): 113-131.

[8] L D Davis. Hand book of genetic algorithms[M]. New York: Van Nostrand Reinhold, 1991: 1-6.

[9] Fleurent C, Ferland J A. Genetic and Hybrid Algorithms for Graph Coloring[J]. Annals of Operations Research, 1995,63(3): 437 463.

[10] 杨启文,蒋静坪,张国宏. GA优化 速度的改进[J]. 软件学报, 2000,12(2): 270-275.

[11] Morgenstem C. Dist ributed Coloration Neighborhood Search[J]. Discrete Mathematic and Theoretical Computer Science, 1996,26(5): 335- 358.

[12] 陈国良,王煦法,庄镇泉,等. 遗传算法 及其应用[M].北京: 人民邮电出版社, 1996: 274-284.★

Research on CPN-based Inter-WBANs Scheduling Algorithm

FAN Wen-Hao1, XIE Zhi-Jun1,2, YU Wen-Bin1

(1. Faculty of Electrical Engineering and Computer Science, Ningbo University, Ningbo 315211, China; 2. Faculty of Engineering, Victoria University, Melbourne 14428, Australia)

Inter-WBANs (wireless body area networks) scheduling can be transformed into CPN (central process node) scheduling to be modeled as a graph coloring problem. A heuristic hybrid genetic simulated annealing algorithm for scheduling was proposed to mitigate the inter-WBAN interference which optimizes WBAN overall performance. In addition, the proposed algorithm was evaluated according to simulation results. Experimental results demonstrate that the proposed algorithm is more applicable for power-consumption and resources limited WBANs.

WBAN inter-WBANs scheduling coloring hybrid genetic

10.3969/j.issn.1006-1010.2015.08.015

TP393

A

1006-1010(2015)08-0069-06

樊文豪,谢志军,俞文彬. 基于CPN的WBANs调度算法研究[J]. 移动通信, 2015,39(8): 69-74.

国家自然科学基金项目（51303157）；宁波市自然基金（2013A610044)；“信息与通信工程”浙江省重中之重学科开放基金资助（xkxl1422）

2014-12-15

责任编辑：刘妙 liumiao@mbcom.cn