卷扬式启闭机卷筒组结构优化设计

2015-12-23吴文龙安徽省水利水电勘测设计院合肥230088

治淮 2015年4期

吴文龙（安徽省水利水电勘测设计院合肥 230088）

科技论坛

卷扬式启闭机卷筒组结构优化设计

吴文龙
（安徽省水利水电勘测设计院合肥 230088）

我国正处于高速发展时期，各行各业都有大量工程需要建设、设备需要制造，设计人员在确保设计产品满足各种规范要求、能够安全可靠运行的前提下，还要千方百计地使产品节省建材，经济合理，节能环保。本文以水利工程常用的卷扬式启闭机卷筒组结构作为优化设计的切入点，介绍了一般工程、设备设计的优化方法。

启闭机卷筒组优化设计目标函数设计变量

1 引言

卷扬式启闭机是广泛运用的一种水利工程闸门起吊设备，其主体仅为一般起重机械的一个起升机构，由驱动装置、传动装置、卷筒组部件、钢丝绳、吊物装置及制动装置等组成。卷筒组部件则由大齿轮、小齿轮、轴、卷筒等构成，是决定卷扬式启闭机机身重量的主要部件。传统的设计方法是依据经验选取或计算各部位尺寸，然后进行强度复核，很难做到用材最省。因此，在满足启闭机生产工艺、结构安全、使用可靠的前提下，对卷筒组各部位尺寸进行优化设计，可以有效地降低启闭机的机重和造价。卷扬式启闭机主体结构示意图见图1。

2 建立数学模型

2.1 建立目标函数

建立一个适当的目标函数来评价设计方案的优劣程度，是机械优化设计的首要问题。对于一般的起重机构来说，应以体积小、重量轻、效率高、造价省为目标。目标函数越多，优化设计越趋完善，但其难度也相应增加。因此，一般不宜取过多目标函数。本文所介绍的优化设计的目标函数是启闭机卷筒组三个主要部件的重量之和。

F（X）=W1（X）+W2（X）+W3（X）

式中，W1（X）、W2（X）、W3（X）分别为大齿轮、卷筒、卷筒轴3个部件的重量相对于设计变量的函数表达式，限于篇幅，不再赘述。

2.2 确定设计变量

优化设计常选取对目标函数有显著影响的独立参数作为设计变量。大齿轮、小齿轮（重量可或略不计）主要取决于齿宽、模数和分度圆直径，而分度圆直径又与小齿轮齿数、模数及传动比有关，因此，把齿宽b、模数m、小齿轮齿数Z1、传动比i等4个参数作为设计变量。至于大齿轮齿数、分度圆直径、幅板厚度、齿圈厚度、轮毂厚度及宽度等要素均可根据齿轮的传统设计方法拟为上述4个变量的函数或定值。卷筒的重量主要取决于卷筒直径、长度和壁厚3个参数，在钢丝绳规格、起升高度确定的情况下，卷筒长度是其直径的一个参数，可见，只要把卷筒直径D、卷筒壁厚δ作为设计变量就能控制卷筒的重量。已知卷筒直径还可相应确定大齿轮与卷筒连接的止口内外径。卷筒轴的重量主要取决于轴径和轴的长度，轴长与卷筒长度、大齿轮宽度以及选定的轴承支承的轴颈长度有关，所以只要把轴径d作为设计变量，便能计算出轴的重量。另外，轴径d对大齿轮的轮毂宽度、卷筒的两端孔径也有影响。

上述7个相互独立的设计变量（在应用中，用户可根据需要增减一些变量）可有效控制卷筒组部件重量的优化问题。其排列如下：

X=（x1，x2，x3，x4，x5，x6，x7）T=（i，Z1，m，D，δ，d，b）T

在这7个设计变量中，i，D，δ，d，b均为连续变量，而模数m有其规定的系列，属离散变量，小齿轮齿数是整形变量。在优化设计过程中，可将离散变量和整形变量均当作连续变量进行优化，待得出结果后，进行圆整，圆整后的各变量也必须满足各项约束条件。

2.3 选取约束条件

图1 卷扬式启闭机主体结构示意图

卷筒组约束条件通常包括刚度、强度、运动学、动力学、工艺、几何安装等，根据现行的卷扬式启闭机设计规范和理论，选取合理的卷筒组重量优化设计约束条件如下：卷筒最小直径约束、卷筒最小壁厚约束、卷筒抗压强度约束、卷筒抗拉强度约束、卷筒抗压稳定性约束、启闭速度上下限约束、电机功率约束、齿宽系数上下限约束、小齿轮不发生根切约束、开式齿轮传动比约束、齿面接触强度约束、齿根弯曲强度约束、钢丝绳偏角约束、安装尺寸约束、卷筒轴强度约束。

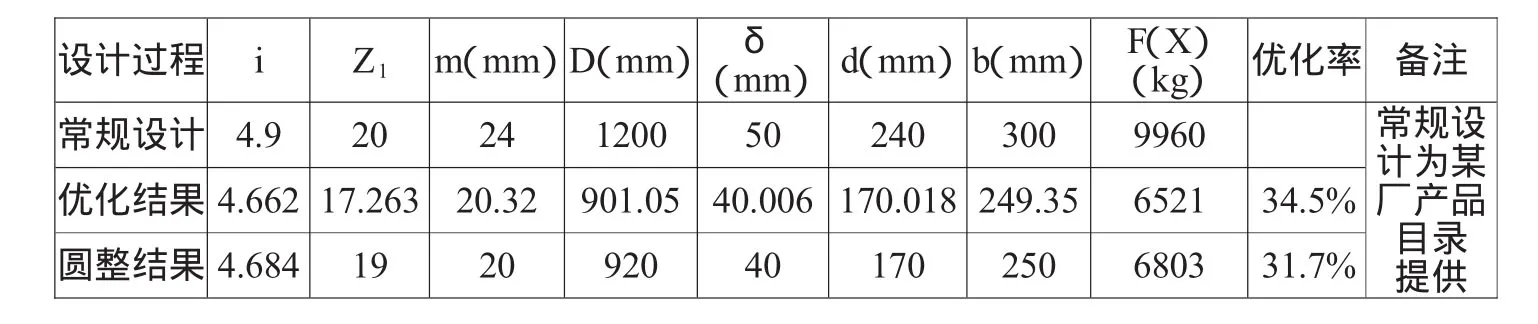
表1 常规设计与优化设计成果对比表

3 选择优化方法

3.1 有约束优化方法选择

卷扬式启闭机卷筒组结构优化设计是一个非线性数学模型，为了提高计算效率，并能达到一定的收敛精度，选择内点形式的混合罚函数法，即把有约束优化问题演变成一个无约束优化问题加以解决。用混合罚函数法求解时，其惩罚函数由原目标函数和包含约束函数的惩罚项组成：

式中：F（X）—目标函数；

G[gu（x）]—不等式约束函数的惩罚项，G[gu（x）]= [gu（x）]-1；

3.2 无约束优化方法选择

通过惩罚函数的处理后，有约束求优问题已变成一个无约束求优问题。无约束求优方法很多，因数学模型非线性程度较高，为避免求导，选择鲍威尔（Powell）法。为防止鲍威尔法中出现“退化”现象，应对新生搜索方向组进行判别。3.3一维优化方法选择

在鲍威尔法无约束求优运算过程中，最终寻优方法还是要进行一维搜索。一维搜索的方法也很多，为便于计算，可利用一个二次插值多项式P（X）来代替原目标函数，然后求出该多项式的极值，以此作为目标函数F（X）的近似极值。经过反复试算，缩小搜索区间，最终取得目标函数极值。

3.4 优化结果圆整

计算机输出的最优结果一般为小数点后的数字很长的数值，在机械制造中无法实现，再加上小齿轮齿数是整形变量，不能有小数，齿轮模数m属离散变量，须符合规定的系列值，因此，必须对计算机输出的各设计变量进行圆整。圆整的准则是：各设计变量尽可能接近优化结果值。圆整后的变量值必须使得各约束条件成立，这一步工作也可以利用计算机进行验证。