基于粗糙集-神经网络的组网雷达作战效能评估

【信息科学与控制工程】

基于粗糙集-神经网络的组网雷达作战效能评估

卞泓斐1，杨根源2，于磊1

(1.海军航空工程学院，山东 烟台264001； 2.海军信息化专家委员会，北京100073)

摘要：建立了组网雷达作战效能评价的指标体系，提出了一种基于粗糙集-神经网络的组网雷达作战效能评价方法，运用粗糙集理论对训练样本进行属性约简，对约简后的属性运用BP神经网络进行训练，该方法能够有效地降低神经网络的复杂度，减少网络训练时间。

关键词：粗糙集；神经网络；组网雷达；效能评估

收稿日期：2014-12-20

作者简介：卞泓斐(1982—),男，博士研究生，主要从事海军兵种信息作战研究。

doi:10.11809/scbgxb2015.06.022

中图分类号：TP183

文章编号：1006-0707(2015)06-0087-06

本文引用格式：卞泓斐，杨根源，于磊.基于粗糙集-神经网络的组网雷达作战效能评估[J].四川兵工学报，2015(6):87-92.

Citationformat:BIANHong-fei,YANGGen-yuan,YULei.EvaluationofCombatEffectivenessofRadarNettingBasedonRoughSetandNeuralNetwork[J].JournalofSichuanOrdnance,2015(6):87-92.

EvaluationofCombatEffectivenessofRadarNetting

BasedonRoughSetandNeuralNetwork

BIANHong-fei1, YANG Gen-yuan2, YU Lei1

(1.NavalAeronauticalEngineeringAcademy,Yantai264001,China;

2.NavalInformationExpertCommittee,Beijing100073,China)

Abstract:Index system for evaluation on the networking radar combat effectiveness was established. An efficiency evaluation method for networking radar combat was put forward based on rough set and neural network. Firstly, applying rough set theory, training samples were reduced by the attribute. Then the reduction attributes were trained by using BP neural network. The above method could effectively reduce the complexity of neural network and the network training time.

Keywords:roughset;neuralnetwork;networkingradar;efficiencyevaluation

所谓雷达组网是指将多部不同体制、不同频段、不同程式、不同极化方式的雷达适当布站，并将所有雷达探测到的各类目标信息经过信息融合，从而完成整个覆盖范围内的探测、定位和跟踪等任务。雷达组网可以扩大空间、时间、频率的覆盖，提高重叠区内空间分辨力和目标发现概率，改善观测精度。然而如何评估组网雷达的作战效能，为合理组网提供有益的参考成为了一个现实的问题。

目前比较常用的效能评估方法有AHP分析方法、组合赋权评估法、模糊综合评估法、灰色关联评估法等，然而这几种评估方法都需要专家对各评价属性的权值进行分配，评估结果难以避免会掺杂个人主观认知的因素[1-6]。神经网络评估方法可以较好地避免以上弊端，同时神经网络还具有较好的非线性运算能力、容错性以及鲁棒性[7-9]，鉴于神经网络的诸多优点，在此采用神经网络对组网雷达的作战效能进行评估。然而在运用神经网络进行效能评估时，当输入数量巨大时，网络计算量也随之迅速增大，为解决这一弊端，这里采用粗糙集理论对所构建的指标体系进行属性约减，然后运用神经网络对约减后的属性进行训练和学习，可以大大减轻运算负担。

1组网雷达作战效能评价指标体系

1.1评价指标设置原则

指标体系确定合理与否将会直接影响到评估结果的准确性，指标体系的规模及指标之间的关联关系会影响到评估过程的复杂性，因此科学合理地确定指标体系是至关重要的。指标体系应满足5个性质：

1) 全面性，以雷达组网后协同作战的角度，从战术和技术上考虑所有可能影响组网雷达作战效能的指标。

2) 客观性，评估指标的设立应根据雷达组网作战的目的以及实践情况，决不能凭借主观臆断。

3) 可行性，指标体系的建立应满足量化计算的可行性。

4) 无冗余性，各指标之间一般不能相互重叠，不能相互包含

5) 极小性，即不能用其他元素更少的指标体系来描述同一问题

1.2组网雷达作战效能评价指标体系

现以雷达组网对空警戒为背景，以实现组网雷达的作战功能为目的，以评价指标选取原则为依据，结合雷达组网作战实践的具体情况，建立对组网雷达作战效能的指标体系如图1所示。

图1　组网雷达作战效能评价指标

2基于粗糙集-神经网络理论的雷达组网作战效能评价模型

2.1 BP神经网络理论

2.1.1BP神经网络的原理及其结构

BP神经网络是基于误差反向传播的多层次前向神经网络。由输入层、隐含层和输出层3层感知器组成，相同层次内的节点不互联，相邻层次的节点之间前向全连接，如图2所示。

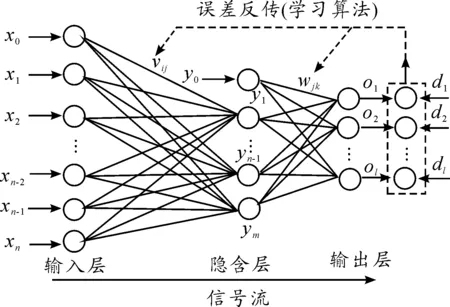
图2　 BP神经网络结构

X=(x1,x2,…，xn)、Y=(y1,y2,…,yl)、O=(o1,o2,…,ol)、D=(d1,d2,…,dl)分别表示输入层输入信号向量、隐层输出信号向量、输出层输出信号向量和期望输出向量即导师信号。V=(V1,V2,…,Vm)、W=(W1,W2,…,Wl)分别表示输入层到隐层的权值矩阵以及隐层到输出层的权值矩阵。

BP神经网络的基本思想是，通过信号的正向传播与误差的反向传播反复修正权值矩阵，达到学习训练的目的。当输出信号向量与导师信号向量的相对误差减小到可接受的程度即停止训练。

2.1.2BP神经网络的算法

1) 正向传播阶段

a) 输入节点的输入：xi；

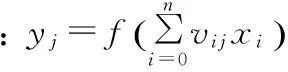
其中wij为连接权值， v0j为隐层节点阈值。

其中:vjl为连接权值；wok为输出层节点阈值。

2) 反向传播阶段

在反向传播阶段，误差信号由输出层通过隐层向输入层传播，将误差沿函数负梯度方向对各层的权值矩阵进行修正。设Δwjk、Δvij分别为输出层及隐层的权值修正量，则有

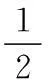
其中η为步长或学习修正率。

2.1.3BP神经网络算法的改进

标准BP算法在调整权值时，只是按当前时刻误差反向传播分摊给各层权值，而没有考虑以前时刻误差梯度方向的影响，从而常使学习训练过程中发生波动，影响训练速度。为此，在权值调整公式中加一动量项，即

其中α为动量系数，且α∈(0,1)。动量项的意义在于使当前时刻的权值调整考虑前一时刻误差调整所积累的经验，避免训练过程中产生波动，提高收敛速度。

2.2粗糙集理论

信息表S=(U,R,V,f)的定义为：U={x1,x2,…,xn}是一个有限非空集合，称为论域对象空间；R是对象的属性非空有限集合，R中的属性可分为两个不相交的子集，即条件属性集C和决策属性集D，R=C∪D；V是属性值的集合，Va是属性的值域；f：U×R→V是信息函数，对于a∈R,x∈U,fa(x)∈Va，它指定了U中每个对象的属性值。

定义1等价关系及等价类

对于∀a∈A(A中包含一个或多个属性)，A⊂R,x∈U,y∈U，它们的属性值相同，即：fa(x)=fa(y)成立，称对象x和y是对属性A的等价关系，表示为：IND(A)={(x,y)|(x,y)∈U×U, ∀a∈A,fa(x)=fa(y)}。

在U中，对属性集A中具有相同等价关系的元素集合称为等价关系IND(A)的等价类，表示为：[x]A={y|(x,y)∈IND(A)}。

定义2上近似、下近似

对任意一个子集X⊆U，属性A的等价类Ei=[x]A有：

下近似为A-(X)={x|[x]A∈X}，上近似为A-(X)={x|[x]A∩X≠Φ}

定义3正域、负域、边界

全集U可以划分为3个不相交的区域，即正域(POS)，负域(NEG)和边界(BND)：

定义4条件属性C相对于决策属性D的正域

设决策属性D的划分A={y1,y2,…,yn}，条件属性C相对于决策属性D的正域POS定义为

POSC(D)=∪C-(yi)

定义5条件属性C相对于决策属性D的约简

若c∈C，如果POS(C-{c})(D)= POSC(D)，则称c是C中相对于D不必要的，即可约简的，否则称c是C中相对于D必要的。

2.3基于粗糙集的神经网络构造

由以上分析可知，在神经网络系统中，其输入空间与输出空间的映射关系不是通过数学模型或显式函数来表达，而是取决于网络的结构、链接强度以及各单元的处理方式，神经网络正是通过对训练集的学习，不断调整网络结构及链接强度，使之不断逼近输入与输出之间的非线性映射关系。由此可见神经网络具有并行及分布式的处理信息能力，并且具有高度的非线性、良好的容错性以及自学习、自组织与自适应性特征。由于影响组网雷达效能评价的因素有空情监控能力、数据处理能力、指挥控制能力、组网综合部署能力、四抗能力、系统生存能力等要素，很难基于现有的数学模型将这些因素进行归纳从而得出组网雷达的综合作战效能，神经网络的非线性、容错性、自学习性以及并行处理的特征能够较好地处理这个问题。但本文中组网雷达的评价指标多达27个，并且训练样本集越多越有利于网络的训练精度，输入空间维数的增大必然使神经网络中的输入层节点数增加，进而导致隐层数及隐层节点数量随之增加，这必然会导致网络规模庞大，增加神经网络训练的负担，造成网络训练时间过长，影响其实用性。而粗糙集中的属性约减算法能够对数据集进行有效地约减，在保留原数据空间有效信息的前提下合理地减小数据空间的大小，简化神经网络输入层的维数。因而本文将两者结合运用，将粗糙集作为神经网络的前置系统[10]，用粗糙集方法对训练集数据进行预处理，简化输入空间维数，然后对简化后的输入空间构建神经网络，其模型如图3所示。

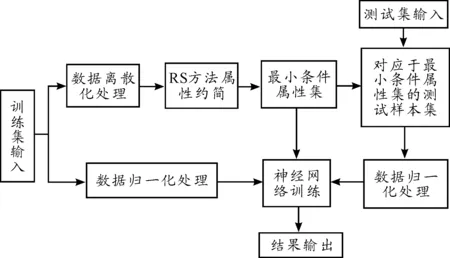
图3　粗糙集-神经网络评估模型

3算例仿真

3.1选取训练样本

3.1.1输入层、隐含层、输出层的设计

BP神经网络输入层和输出层神经元的个数是由输入和输出向量的个数决定的，输入即组网雷达作战效能评价的27个指标，输出为组网雷达作战效能评价的结果。为突出运算过程，简化运算复杂度，选用空情监控能力为例进行神经网络建模，即本例中输入个数为6，输出个数为1。隐含层神经元的数目至今没有一个明确的规定，可参考如下经验公式对隐层神经元数目划定大致范围：

通过神经网络训练对比确定相对合适的隐层神经元数目。

3.1.2选取训练样本

由于BP神经网络是通过期望输出信号与实际输出信号的相对误差进行比对来进行学习而不断调整网络结构的，因而训练样本的选取直接关系到评估结果的准确性与可信度。为了保证评估结果符合客观实际，选取了组网雷达10种不同状态的各指标数据作为神经网络的输入，并通过若干专家打分的方法得出每种状态下的作战效能作为输出。表1列出了不同状态下组网雷达各指标值及作战效能。

表1　组网雷达作战效能原始关系表

3.2训练样本属性约减

3.2.1离散化训练样本

由于粗糙集所分析的数据只能是离散数据，因此必须对数据表中的数据进行离散化处理，数据离散化的方法主要有等距离算法、等频率区间法、模糊聚类法、NaiveScaler算法等。本文采用等距离算法结合专家经验进行数据的离散操作。离散化后的训练样本决策如表2所示。

3.2.2决策表属性约减

令C={a1,a2,a3,a4,a5,a6},D={d}

则

IND(C)={{1},{2},{3},{4},{5},{6},{7},{8},{9},{10}}

IND(D)={{1,8},{2,6},{3},{4,9,10},{5,7}}

Posc(D)=U

1) 计算缺少一个属性的等价关系

IND(C{a1})={{1,8},{2,4},{3},{5},{6},{7},{9},{10}}

IND(C{a2})={{1,8},{2},{3,6},{4},{5,7},{9},{10}}

IND(C{a3})={{1,8},{2},{3},{4},{5},{6},{7},{9},{10}}

IND(C{a4})={{1,8},{2},{3},{4},{5},{6},{7},{9},{10}}

IND(C{a5})={{1,3,8},{2},{4},{5},{6},{7},{9},{10}}

IND(C{a6})={{1,8},{2},{3},{4},{5,10},{6},{7}{9}}

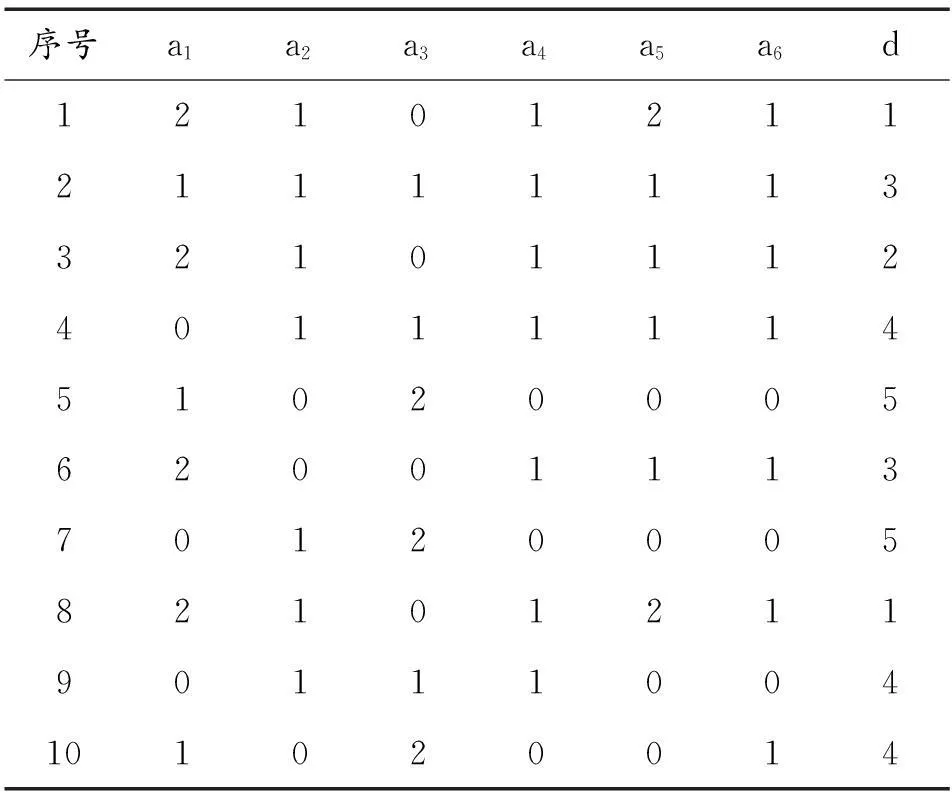
表2　离散化样本数据后的关系表

2) 计算缺少一个条件属性相对于决策属性的正域

Pos(C{a1}) (D)={1,3,5,6,7,8,9,10}≠U

Pos(C{a2}) (D)={1,2,4,5,7,8,9,10}≠U

Pos(C{a3}) (D)=U=Pos(C)(D)

Pos(C{a4}) (D)=U=Pos(C)(D)

Pos(C{a5}) (D)={2,4,5,6,7,9,10}≠U

Pos(C{a6}) (D)={1,2,3,4,6,7,8,9}≠U

由此可知，属性a3、a4是相对于决策属性d是可以省略的，但不一定是可同时省略。属性a1、a2、a5、a6相对于决策属性d是不可省略的，因此Core(c)={a1,a2,a5,a6}。

3) 计算同时减少{a3,a4}等价关系的正域

IND(C{a2,a3})={{1,8},{2},{3},{4},{5},{6},{7,9},{10}}

Pos(C{a3,a4}) (D)={1,2,3,4,5,6,8,10}≠U

说明{a3、a4}是不可同时省略的。在{a3、a4}中只能删除一个属性，即存在2个约简

redD(C)={{a1,a2,a3,a5,a6},{a1,a2,a4,a5,a6}}

3.3神经网络训练

3.3.1归一化训练样本

从以上分析可以看出各个评估指标的量纲是不同的，即神经网络输入数据的单位不一样，其原始数据之间可能存在较大差异；另外，由于对抗性不同，有些指标是越大越优，而有些则越小越优，因此直接将其用于评估可能会使得评估结果不确定，从而失去评估的意义。所以有必要在评估前对评估指标的原始数据进行适当的预处理，消除上述的影响后再进行评估。

本文采用极差变换法来消除量纲，在消除量纲的同时将所有数据转变为越大越优，从而有利于下一步价值评估的展开。

效益型指标即指标值越大其价值越大的指标，如最大探测距离、目标发现概率等，其变换方法为

成本型指标即指标值越大其价值越小的指标，如定位精度，其变换方法为

按照上述方法得出的归一化矩阵如表3所示。

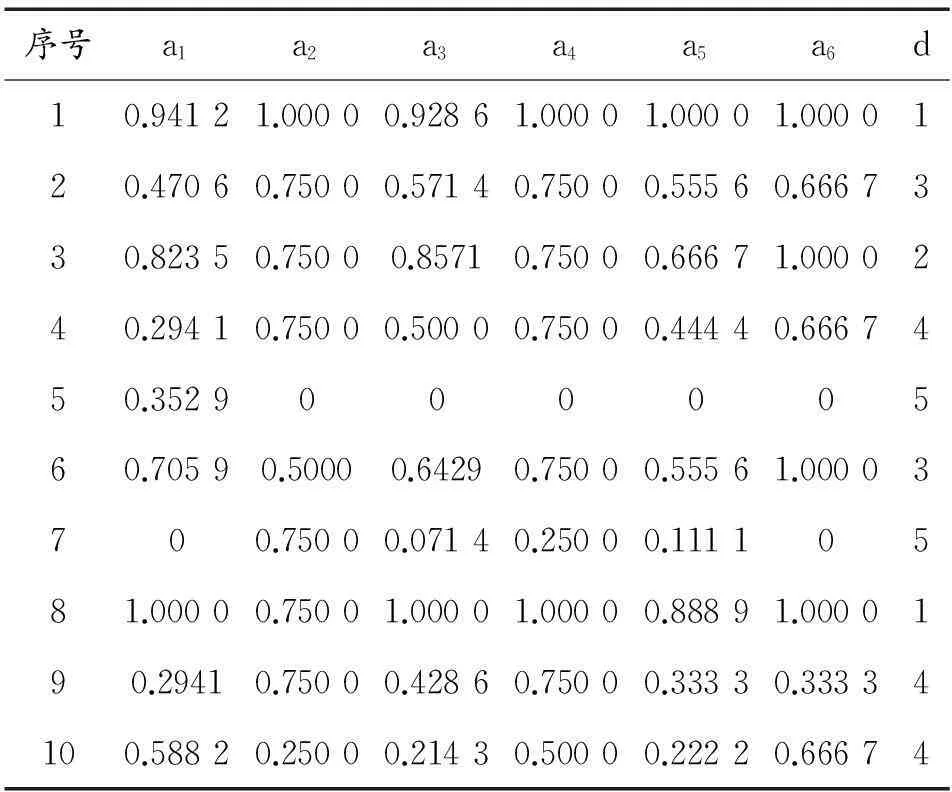
表3　归一化样本数据后的关系表

3.3.2神经网络训练

根据神经网络算法，将表3中约简后的属性{a1,a2,a3,a5,a6}前10组数据作为训练样本，利用Matlab软件进行仿真，输入层与隐含层之间采用tansig作为传递函数、隐含层与输出层之间采用logsig作为传递函数进行训练，学习速率为0.05，学习精度为 0.000 01，隐含层采用6个神经元，当网络模型的识别精度满足要求，即可输出迭代次数、连接权值及各层的阈值。此时Matlab输出的神经网络结构如图4所示。神经网络训练过程如图5。

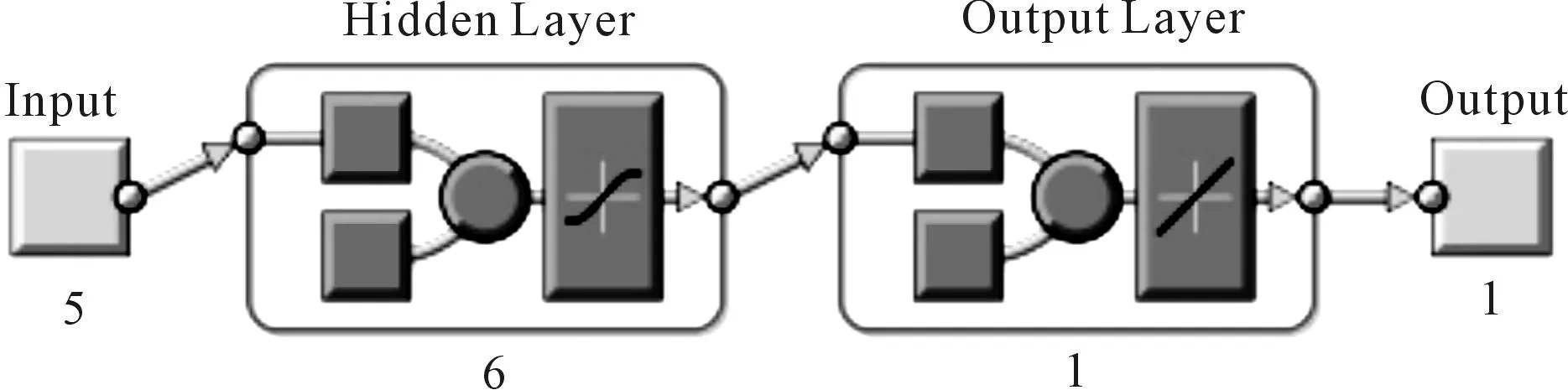
图4　神经网络训练结构

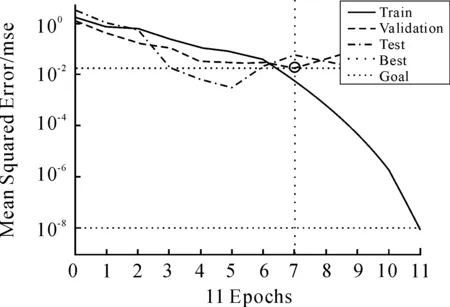
图5　神经网络训练过程

得到的BP神经网络的权值和阈值为：

输入层到隐含层的权值

隐含层到输出层的权值

w2=-0.951 60.122 6-0.685 60.484 3

0.160 40.031 0

输入层到隐含层的阈值

B1=-2.220 7-1.132 10.847 10.408 6

-1.175 92.495 3

隐含层到输出层的阈值

B2=-0.288 2

由结果可见，经过粗糙集属性约减后的神经网络经过11次迭代即可达到训练精度，具有较快的收敛速度。

3.4综合评估

对于待评估的某一状态下的组网雷达作战效能，只需把把各指标参数输入已经训练好的神经网络，神经网络将会根据训练所得的各权值与阈值自动计算出评估结果，然后根据最大隶属度原则确定所属的评定等级。选取5个状态下的组网雷达参数进行评估，并先由专家对各状态的作战效能进行评估得出如表4所示。

表4　测试样本表

通过模型计算，神经网络输出值及专家评估值对比如表5与图6所示。

表5　测试结果与专家评估值对比表

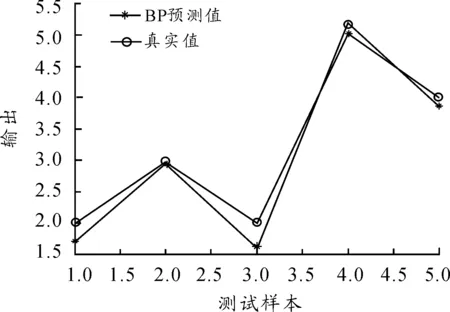
图6　神经网络预测指与真实值比较

经过粗糙集属性约减后的神经网络输出值与专家评估基本吻合，该模型满足实际使用要求。

4结束语

本研究提出了一种基于粗糙集-神经网络的组网雷达作战效能评估模型并给出了相应的算法，该模型首先利用粗糙集理论在处理冗余信息以及属性约简方面的优势对原始数据表进行智能数据分析，去掉原始数据表中的噪声干扰及冗余属性，提取最简属性集，然后对约简后的属性集作为训练样本运用神经网络进行训练，这种方法有效地减少了网络的输入层神经元数量，从而达到减少隐含层及隐含层神经元数量的目的，有效地降低了神经网络训练的复杂性，提高了训练速度及准确率。

参考文献：

[1]周琳,徐进,马艳琴,等.雷达组网探测系统综合效能评估方法研究[J].电子工程师,2007,33(9):10-13.

[2]张培珍,杨根源,张扬,等.雷达组网效能量化评估模型[J].现代防御技术,2010,38(5):5-10.

[3]梁宇,李保林,王军胜.基于神经网络的大区域防空信息进攻作战效能评估[J].现代防御技术,2006,34(3):9-13.

[4]邓堃,吴静.基于云理论的雷达组网作战效能评估[J].火力与指挥控制,2007,32(11):81-84.

[5]刘帅,寇英信,付昭旺,等.基于人工神经网络的空战效能评估[J].电光与控制,2010,17(4):26-29.

[6]刘健,辛永平.主成分分析的雷达组网作战效能评价模型[J].火力与指挥控制,2011,36(6):35-38.

[7]黄晶晶,熊才权.粗糙集-神经网络在作战效能评估中的应用[J].计算机与数字工程,2011,39(5):62-65.

[8]董奎义,王子明,杨根源.基于粗糙集与神经网络方法的空袭目标类型识别模型研究[J].电光与控制,2011,18(1):10-13.

[9]江雷,任德奎,张宁,等.BP神经网络在装备保障性评估中的应用[J].四川兵工学报,2014,35(10):74-76.

[10]郭天虎,张笃涛.基于粗糙集的后勤装备保障效能评估指标体系的简化[J]四川兵工学报,2009,30(6):122-124.

(责任编辑杨继森)