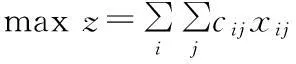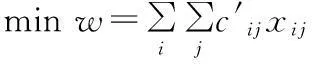基于匈牙利算法的战时运油车前送油料调度优化模型研究

2015-12-23李开红,肖辉,李横等

兵器装备工程学报 2015年6期

关键词：模型

【后勤保障与装备管理】

李开红1,肖辉2，李横1，胡汝翼1，郭鹏1

(1.后勤工程学院军事油料应用与管理工程系，重庆401311;

2.西藏军区后勤部军需物资油料处，拉萨851600)

摘要：战时运油车前送油料调度优化，是一个综合考虑部队用油需求、战场环境、地形、路径等多因素，追求保障的安全性和时效性等多目标的保障决策问题；在复杂战场条件下，战区应急保障旅油料营通常编成若干个功能齐全、机动性好的小型机动支援油料保障分队，充分利用公路交通网分散配置，形成“网状部署”，针对在不同作战地域担负不同作战任务的部队，快速、灵活、安全地实施油料支援保障；通过构建基于匈牙利算法的战时运油车调度模型，当获取多个作战部队的油料补给实时需求后，可自动在满足条件的所有保障分队中进行快速匹配，为决策者提供最佳保障策略建议；经Matlab仿真和实例分析验证，该模型在解决战场油料前送实时调度问题上是一个非常有效的方法。

关键词：匈牙利算法；运油车；前送油料；调度优化；模型

作者简介：李开红(1985—)，男，硕士研究生，主要从事油料勤务研究。

doi:10.11809/scbgxb2015.06.016

中图分类号：E917

文章编号：1006-0707(2015)06-0061-05

本文引用格式：李开红,肖辉，李横，等.基于匈牙利算法的战时运油车前送油料调度优化模型研究[J].四川兵工学报，2015(6):61-65.

Citation format:LI Kai-hong, XIAO Hui, LI Heng,et al.Scheduling Optimization Model of Forward POL Transportation by Oil Tank Car on Wartime Based on Hungarian-Algorithm[J].Journal of Sichuan Ordnance,2015(6):61-65.

Scheduling Optimization Model of Forward POL Transportation

by Oil Tank Car on Wartime Based on Hungarian-Algorithm

LI Kai-hong1, XIAO Hui2, LI Heng1, HU Ru-yi1, GUO Peng1

(1.Department of Petroleum Application and Management Engineering,

Logistic Engineering University, Chongqing 401311, China; 2.Military Supplies and Oil Office,

Tibet Military Logistic Department, Lhasa 851600, China)

Abstract:The scheduling optimization of forward POL transportation by oil tank car on wartime is a comprehensive consideration of many factors such as oil demand from army, battlefield environment, terrain, route, etc, and it pursuits a multi-targets of time and security support decision problem. In the complex battlefield conditions, the theater emergency support brigade POL support battalion usually consists of several complete function, good maneuver flexibility and little scale POL support units to make full use of highway traffic network distributed configuration and to form a “net deployment” to implement fast, smart and safe POL support according to the different combat mission armies in different region. By constructing a scheduling model of oil tank car on wartime based on the Hungarian algorithm, when the system obtain the real-time fuel supply requirement from combat troops, it will automatic quick matching in POL support units which satisfying the conditions to provide the best guarantee strategy for decision maker. By Matlab simulation, it was proved that it is a very effective method in solving the decision problem of real-time scheduling of forward transport POL by oil tank car.

Key words: Hungarian algorithm; oil tank car; forward POL transportation; scheduling optimization;

model

战时运油车的调度问题是一类高难度的运输决策问题，军内外对这类问题的研究比较多，研究的主要方法有：单纯性法，排队论，图论，遗传算法[1]等。2005年，后勤工程学院的李萌等提出的联合战役油料输送系统模拟模型及优化研究[2]，就是采用排队论的方法，将联合战役油料输送视为一个由多个子系统组成的排队系统，综合考虑了各种运输工具[3]的选取，提出了最经济的运输方案；2006年，李横等发表的联合战役野战油库部署多目标优化模拟模型[4]，也是基于排队论提出了战役野战油库向部队油料输送力量的分配模型，属于一对多式保障，研究重点是如何分配使运油车数最少；2012年，王强等发表的《基于GPSSW的油料运输力量模拟模型》[5]中，提出了后方油库与战役野战油库之间进行油料输转的一种运输模型，且只限于研究单个路径中一对一式油料运输问题。上述文章中，虽然从不同侧重点分别研究了战时油料保障的各个环节，但均未考虑前送油料这类战场末端保障问题，也未深入研究战时油料保障的安全性和时效性等战场特殊性要求。而且采用的计算机模拟方法效率比较低，比如GPSSW仿真方法[6]需进行反复模拟，得出最优解的速度较慢，而如果初始解选取不合适的话，甚至很难求出最优解，因此需要一种更高效的匹配方法，来解决这类多路径多目标的油料运输决策难题。匈牙利算法就是一种高效的匹配算法，以二分图为理论基础，总能在有限步内收敛于最优解，而且不依赖初始解的选择，在解决最佳匹配问题上具有快速、高效的特点，通常得出的最终解就是完美匹配。

目前，采用匈牙利算法对运输车辆调度问题进行研究的还不多，主要有：2009年，武警工程学院的徐小林[7]提出的基于匈牙利算法的多车型车辆调度问题；2010年，北京交通大学的于焕英[8]提出的基于匈牙利算法的多车型配送问题。以上研究都是基于匈牙利算法建立以最小总油耗量为目标函数的车辆调度决策模型，目的是以最低的费用完成运输工作，主要考虑的是经济效益；在战时条件下油料前送的车辆调度需考虑的因素重多，如果仅仅考虑经济效益明显是不科学、不适用的，而且需要考虑的因素越多，其复杂程度可能就呈几何级数增加。因此，从战时油料保障的实际情况来分析，建立运油车的调度模型时必须考虑的主要因素是运油车调度的时效性和安全性。

1战时前送油料支援保障分析

1.1保障实体

本文的研究对象是战区应急保障旅油料营，它是由战区联勤分部抽组的综合性战役后勤油料应急机动保障部(分)队，具有较强的快速反应能力、机动保障能力和综合保障能力，是一支应急支援保障的“拳头”力量[9]。着眼未来战争爆发突然、应急机动部队行动紧急、携行油料较少、在集结地域停留时间短等特点，要求应急保障油料营必须在任何情况下都能作出快速反应，与机动部队同步反应，实施穿插补给任务，必须以最快的速度在最短的时间内为作战部队提供有力补给，赢得宝贵时间、创造获胜条件。

1.2保障模式

战时油料前送支援保障通常需保障战役军团多方向、多地域、多地点作战，因此，根据区域空间和可能担负的机动支援油料保障任务，将应急机动支援油料保障力量小型化、模块化，按照“合成、混编、超常”的要求，以定点保障点为依托，优化组合，编成若干个功能齐全、机动性好的小型机动支援油料保障分队，充分利用交通网分散配置，形成“网状部署”，针对在不同作战地域担负不同作战任务的部队[10]，快速、灵活、安全地实施前送油料支援保障，为作战部队快速反应赢得宝贵的时间。

未来信息化战争中，随着野战单装定位与油料动态监控系统[11]的成功应用，配合先进的定位设备和数据采集设备，可以实时收集作战部队的地理位置、油料需求量和油料保障分队的地理位置、最大保障能力，实现战场油料保障需求和保障资源的“可视化”。一旦多个作战部队同一时间内提出油料补给需求后，系统可自动在满足条件的所有保障分队中进行快速匹配，得出最佳保障策略，从而为决策者提供科学、合理的决策建议。

2基于匈牙利算法的调度优化模型

2.1匈牙利算法

匈牙利算法是匈牙利数学家Edmonds提出的，该算法的核心是基于Hall定理中充分性证明的思想来寻找增广路径求最大匹配。匈牙利算法的理论基础是在效益矩阵的任何行或列中，加上或减去一个常数后不会改变最优分配。它的基本思想是修改效益矩阵的行或列，使得每一行或列中至少有一个为零的元素，经过修正后，直至在不同行、不同列中至少有一个零元素，从而得到与这些零元素相对应的一个完全分配方案。当用于效益矩阵时，这个完全分配方案就是一个最优分配。

求最大匹配的一种常见的算法是枚举法：先找出全部匹配，然后保留匹配数最多的。但是该算法的复杂度为边数的指数级函数，求解具有n个变量的问题时需枚举2n种可能。相比其他算法，匈牙利算法的最大优点是总能在有限步内收敛出一个最优解。它在解决复杂网络结构和实时性要求比较高的问题时，速度很快，效果明显。经计算机模拟仿真结果证明，当数据量n急剧加大时，时间复杂度变化不大，耗时相对较少，它在解决该多目标匹配问题时具有非常明显的优势。

2.2模型构建

2.2.1问题描述

战时运油车前送油料的调度优化，是一个综合考虑部队用油需求、战场环境、地形、路径等多因素，追求保障的安全性和时效性等多目标的保障决策问题[12]，任何一个参数的改变都可能影响最终的决策结果。该类问题可简化描述为：

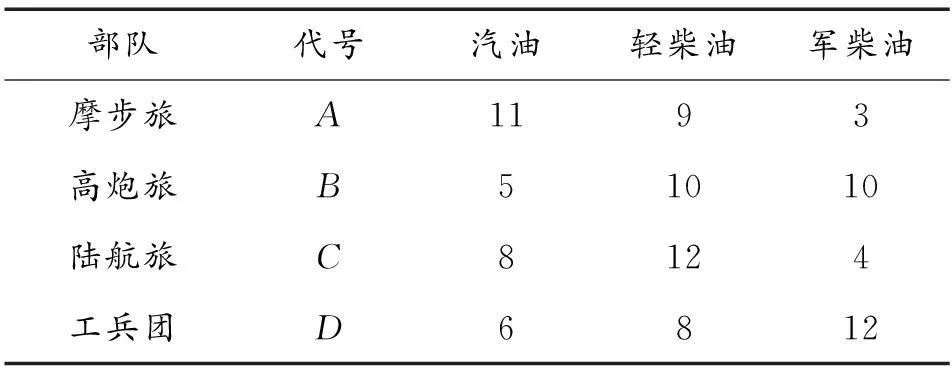
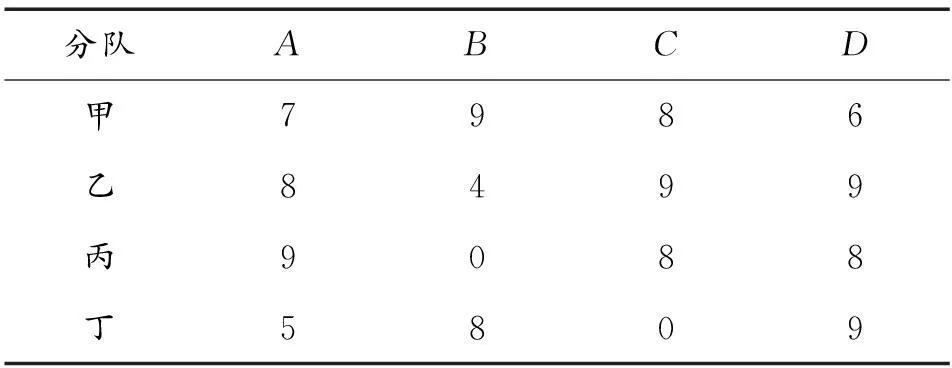
设有N个处于不同地域的作战部队X= (X1,X2,…,Xn) 同一时间内提出油料补给需求，现安排M个油料运输分队Y= (Y1,Y2,…,Ym) 向上述N个单位前送油料，规定必须在t时限内完成补给任务，已知相对路径矩阵C和路径安全矩阵P，如何调度分配运油车使得当前油料保障军事效益最大化。

2.2.2调度模型

该问题涉及因素很多，采用传统的数学解析方法难以得出准确的答案，战场最重要的因素是油料保障的安全性和时效性，即保证任务安全的基础上使运输时间的最小化是实现保障效能最大化的根本途径。因此，该问题的关键因素是考虑在战时确保安全前提下前送油料的时效性，因此可转化为已知路径矩阵C，通过构建安全矩阵P，求得等效时间矩阵T的最小值问题。模型目标方程：

约束条件如下：

1)N为需求油料的作战部队数，M为油料保障分队数，i为第i个保障分队，j为第j个需求部队，k为第k种油品；

2)A为每个作战部队的油料需求矩阵，Ajk代表j部队的k油品(汽油，轻柴油，军柴油等)的需求数量；

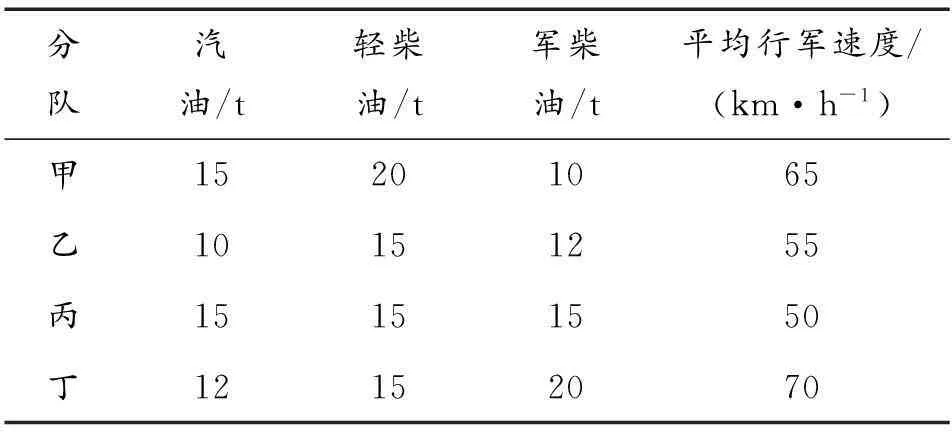
3)B为每个分队的油料保障能力矩阵，它满足：运输分队i的k油品剩余量应不少于i部队的需求，Ajk≤Bik；B的最后一列是保障分队的行军速度：vi=Bin；

4)C为相对路径矩阵，Cij代表Yi分队向Xj部队前送油料时的路径权值，道路遭敌破坏，或油料保障分队的保障能力无法满足需求时，其权重可设为一个极大值，即Cij=Max；

5)P为路径的安全系数矩阵，根据战场情报，由专家打分得出，评分越高越安全；

6)T为时间矩阵，它由路径矩阵和安全矩阵计算得出：tij= (cij/vi) /pij，满足0 ≤tij≤tmax；

7)Z为派遣矩阵，它是标准的单元矩阵，即只存在一一对应关系。

2.3模型求解

2.3.1模型求解方法

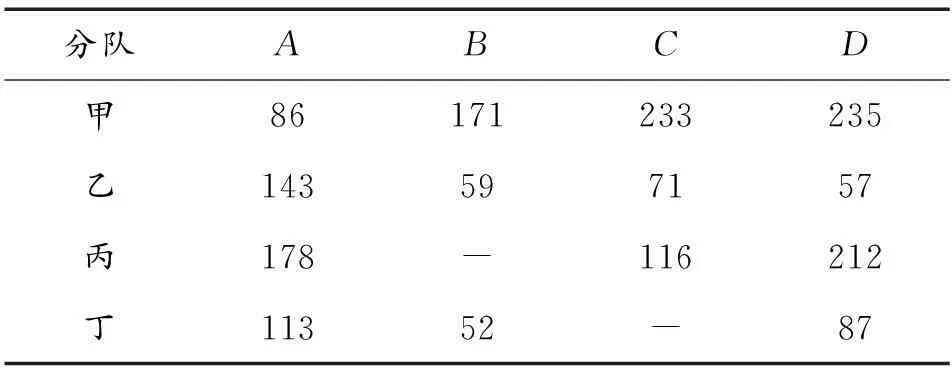
1) 构造平衡的相对路径矩阵C。因匈牙利算法擅长解决平衡问题，当保障分队数和需求部队数不对等时，可通过构造虚拟的保障分队或需求分队，重新建立平衡路径矩阵C＇。具体解法如下：

① 若N>M，则一个分队可能需保障多个部队的油料前送，可虚拟N-M个运油分队，构造新的路径平衡矩阵C＇={Cm×n|C(n-m)×n}即可。

② 若N

③ 若N=M，则属于平衡问题，可直接由匈牙利算法求解。

④ 模型转化，若对应的模型是求最大值，可将其变换为求最小值。

2) 修改相对路径矩阵C。如果道路不通或者油料保障分队当前剩余油料少于作战分队需求，则可修改路径矩阵C，将其对应的权重设置为最大值。即满足：

3) 对安全性量化评估，建立路径安全矩阵P

在信息化战争条件下，公路交通网是敌方打击的首要目标，而由于战场路况和敌情的错综复杂，运油分队被敌发现进而遭打击的概率会显著增大，其安全面临着前所未有的挑战，因此，必须对路径的安全性进行科学评价。采用德尔斐法，通过实时收集战场情报、作战分队报告情况、咨询经验丰富的部队油勤人员和指挥参谋人员等多种途径，历经咨询、反馈、决策的循环过程，依据表1所示的安全评估指标体系，运用层次分析法[13]，可建立初步的路径安全评分矩阵S。得出各条道路的安全系数矩阵后，再进行归一化处理，即令Pij=Sij/Smax，即可建立归一化的安全矩阵P。

表1　安全评估指标

注：满分10分。

4) 时间矩阵T可由路径矩阵C和安全矩阵P直接计算得出。

其中vi=Bin。

根据目标函数最优解，得出派遣矩阵Z。

2.3.2Matlab编程实现

本文采用Matlab来模拟该问题[14]，要将基于实际油料业务工作的数学模型转化为Matlab程序，需要构建满足匈牙利算法的关键计算模块，通过反复模拟，并对输出结果进行统计分析，从而得出合理、可行、实用的结论。

Matlab关键代码如下：

1) 时间矩阵构造。时间矩阵构造如下：

function[D,T]=Panbie(A,B,C,P)

[m1,n1]=size(A)

[m2,n2]=size(B)

tmax=100

cmax=1000

forj=1:m1

fork=1:n1

fori= 1:m1

ifA(j,k)>B(i,k)

C(i,j)=Cmax

end

D(i,j)=C(i,j)

Ifp(I,j)=0

T(i,j)=tmax

else

T(i,j)= (D(i,j)/B(i,n2))/P(i,j)

end

2) 匈牙利算法的关键实现。

function [Matching,Cost] = Edmonds(T)

function [P_cond,stepnum] = step1(P_cond)

function [r_cov,c_cov,M,stepnum] = step2(P_cond)

function [c_cov,stepnum] = step3(M,P_size)

function [M,r_cov,c_cov,Z_c,stepnum] = step4(P_cond,r_cov,c_cov,M)

function [M,r_cov,c_cov,stepnum] = step5(M,Z_r,Z_c,r_cov,c_cov)

function [P_cond,stepnum] = step6(P_cond,r_cov,c_cov)

function cnum = min_line_cover(Edge)

function[D,T]=Panbie(A,B,C)

3实例分析

3.1实例描述

假想XX边境地区发生武装冲突，某战区XX集团军奉命进入边境地区执行反击作战任务。某次战役中该集团军受领任务需多线同时作战，所属部队分别部署于4个不同方向地域，因战斗比较激烈，油料消耗巨大，现有4个作战单位油料即将消耗殆尽，分别是摩步旅，高炮旅，高炮旅，工兵团(代号分别是A,B,C,D)，同时向后方指挥部提出油料补充需求(表2)。后方指挥部油料助理员根据指挥部命令，现紧急派遣4个油料保障分队(代号分别是甲，乙，丙，丁)，为作战部队前送油料，要求必须在4 h内完成补给任务。现已给出各油料保障分队距离作战部队的相对路径(表3)及其最大保障能力(表4)，由情报系统给出的路径安全系数评分(表5)，试问，如何进行调度，确保在完成任务的基础上使运输时间最短。

表2　作战部队油料需求　t

表3　保障分队距作战部队距离　km

注：“-”代表因道路被敌方破坏，车队无法到达。

表4　保障分队当前保障能力

注：因分队车辆种类不同，所以平均行军速度略有不同。

表5　路径安全系数评分

注：得分越高，代表越安全，满分10分，0分代表该路径不通。

3.2求解过程

第1步：因道路受损的约束条件筛选出路径(丙-B，丁-C)无法完成保障任务，根据分队的保障能力约束条件，可筛选出路径(甲-D，乙-A)无法完成保障任务。将无法达到的路径值直接设置为极大值，这里设为1 000即可。由此可建立路径矩阵C：

第2步：对评分矩阵进行归一化处理，得出安全矩阵P：

第3步：代入行军速度和安全矩阵P，可计算出时间矩阵T:

第4步：利用匈牙利算法对时间矩阵T进行求解：

ABCD甲1.892.924.4825.63乙22.732.681.431.16丙3.961002.905.30丁3.220.931001.38=01.042.5923.7521.571.520.2801.0697.1002.402.30099.070.45

第5步：由此得到最佳的派遣矩阵Z为：

ABCD甲1000乙0001丙0010丁0100

3.3最佳解决方案

由此得出最佳的匹配方案是：甲—A，乙—D，丙—C，丁—B。最短用时分别是：1.89 h，1.16 h，2.9 h，0.93 h，均满足时限要求，总的耗时为6.88 h。

4结论

本文从战时油料前送支援保障流程入手，重点针对战场环境下油料前送支援保障的安全性和时效性建立目标函数，采用匈牙利算法构建了运油车调度模型，首先基于战场环境因素和保障能力制约对路径矩阵C进行筛选，再根据战场情报和专家打分建立路径安全矩阵P，并由此建立时效性等效矩阵T，然后利用匈牙利算法对等效矩阵T进行求解得出了派遣矩阵Z，最终得到合理的决策方案建议。经MATLAB模拟仿真和实例分析验证，该模型能够快速形成科学、合理的派遣方案和决策建议，在解决战场油料前送实时调度问题上是一种更加高效的方法。但仍有需要进一步深入研究的内容：

1) 路径安全矩阵P的构建依赖专家打分，不同的人会有不同的意见，一个细小的判断错误将会导致重大决策失误，在战争中甚至可能造成灾难性后果。因此，专家选取必须是有丰富经验并对战场情况有清晰判断的保障指挥员。同时，建立可靠的战场情报搜集和预警分析体系也非常必要。

2) 本模型只考虑了安全性和时效性两个因素，而战场因素是错综复杂的，需考虑的问题很多，作为战场后勤保障指挥员必须全局考虑，抓住关键因素，才能实现高效无缝链接式油料保障。

参考文献：

[1]张亮,周继宝.基于遗传算法的后勤运输车路径规划[J].四川兵工学报,2012,33(2):81-83.

[2]李萌,李少鸣,李横.联合战役油料输送系统模拟模型及优化研究[J].后勤工程学院学报,2005,21(3):89-92.

[3]王富平,李横,李少鸣,等.战时铁路运输油料抢收模拟优化[J].后勤工程学院学报,2010,26(6):40-43,77.

[4]李横,苏永东.联合战役野战油库部署多目标优化模拟模型[J].后勤工程学院学报，2005,21(3):89-93.

[5]王强,李横,龙智强,等.基于GPSSW的油料运输力量模拟模型[J].物流科技,2012(7):119-123.

[6]郝亮,王静,周庆忠.基于GPSSW的油料装备战场维修力量优化分配[J].四川兵工学报,2010,31(3):18-21.

[7]徐小林.基于匈牙利算法的多车型车辆调度问题[J].火力与指挥控制,2009,34(2):137-139.

[8]于焕英,孙晚华,何峣.基于匈牙利算法的多车型配送问题[J].物流技术,2010(11):74-75.

[9]黄海波,李少鸣.联勤分部应急机动支援油料保障研究[D].重庆:后勤工程学院.2006.