基于协方差矩阵表示的图像集匹配
2015-12-22詹增荣曾青松
詹增荣,曾青松
(广州番禺职业技术学院信息工程学院,中国广州 511483)
对象识别是模式识别领域中非常重要的应用之一.随着摄像机的广泛应用,人们可以轻易地获取关注对象的大批量监控图像,这一背景促进了人们从单一图像为输入[1]转向以图像集合为输入[2-4]的对象识别应用研究.
以图像集合为研究对象的匹配方法能够利用多幅图像提供的信息获得更好的匹配性能[5].这一类问题的研究一般通过对单幅图像提取特征,然后合成多幅图像的特征组成一个图像特征集合,建立图像集合的模型,通过计算模型对之间的距离来度量两个集合的相似性[6].在实际应用中,获取的图像集中通常含有噪声,会影响模型的描述能力,因此所构建的模型应该要有一定的鲁棒性,或者低秩描述[7]来表示一个图像集合.
一般地,可考虑使用子空间或流形来表达一个图像集合[8].经典的互子空间(Mutual subspace method:MSM)方法[4]将图像集投影到低维线性子空间,通过计算图像序列生成的子空间之间的主角来度量两个子空间之间相似性,这一方法被广泛地扩展.流形-流形距离(Manifold-Manifold Distance:MMD)[9]扩展了子空间距离,将整个非线性流形划分成多个局部模型[10],综合考虑成对的局部模型之间的距离来度量两个流形的相似性.作为MMD 的扩展,通过用流形来描述每一个集合,流形鉴别分析[11](Manifold Discriminant Analysis:MDA)通过多流形学习解决有监督的流形间距离计算问题.仿射子空间方法,如基于仿射包的图像集距离[12](Affine Hull-based Image Set Distance:AHISD),通过两个仿射包中距离最近的两个点之间的几何距离来度量集合之间的相似性.为了克服AHISD 方法由于不加任何额外约束条件,直接搜索最近邻的点,导致离群点的干扰严重影响分类的精确度的缺陷,借助稀疏表达的方法,通过稀疏逼近最近邻点[13](Sparse Approximated Nearest Points:SANP)可以更加精确地度量两个仿射包之间的相似性.
本文从图像集合的整体特征模型出发,考虑到正定的对称矩阵构成黎曼流形上的子空间,使用图像的特征向量构成图像集合的特征矩阵,然后计算特征矩阵的协方差来建模图像集合.通过定义协方差矩阵对之间的对数距离来度量两个图像集合的相似性,有效地将黎曼流形上的度量转换为欧式空间上的度量,应用核Fisher 判别分析(Kernel Fisher Discriminant Analysis:KFDA)[14]进行分类.
1 图像集合的特征描述
1.1 单幅图像的特征描述
给定一个固定位置的摄像机,由于场景的光照、观测对象的姿态变化,连续获取的图像之间存在很大的差异,但是它们之间也存在很大的相关性.因此,需要对观测对象的图像进行特征提取,以尽可能地消除外界因素的影响.提取图像特征最简单的办法是将图像进行灰度变换、直方图均衡化,然后将图像的像素值逐列堆叠成一个向量来表示,也可使用其他的图像特征提取方法对整个图像提取局部特征,如局部二值模式[15](Local Binary Patterns,LBP)、尺度不变特征变换(Scale-Invariant Feature Transform:SIFT).LBP 是一种有效的纹理描述算子,度量和提取图像局部的纹理信息,对光照具有不变性,SIFT 是一种检测局部特征的算法,通过求一幅图像中的特征点,一般也称为兴趣点(interest points)或者角点(corner points),及其有关尺度(scale)和方向(orientation)的描述子得到图像的特征描述.
1.2 图像集合的表达
在得到单幅图像的向量化特征描述基础上,对于图像集合,一种简单的处理方法是将这些向量作为矩阵的列,通过一个矩阵来表示,计算基于矩阵分解的特征,建立特征模型,然后定义两个模型之间的相似度.基于矩阵描述的方法的主要优点是可以利用已有的成熟的矩阵分解技术,图像集之间的相似性转化为两个矩阵之间的相似性的度量.
由于图像集合的元素数量不确定,直接计算两个尺度不一致的特征矩阵的相似性有一定的困难.考虑到矩阵的协方差体现了变量之间的二阶统计特性,反映了集合中各图像之间的相关性,因而可以通过计算特征矩阵的协方差来建模一个图像集合得到大小一致的协方差矩阵.进一步,由于正定对称矩阵构成黎曼流形的子空间,每一个矩阵可以理解为流形上的一个点,非奇异协方差矩阵是对称正定矩阵,所以使用协方差矩阵描述一个图像集,可以将图像集合的相似性计算转换为计算流形上两个点之间的距离[6].
将图像集合的协方差矩阵当成黎曼流形上的点,可以解释为:存在一个非线性映射函数将图像集合X投影到特征空间,表示为协方差矩阵模型cov(X),这个函数描述为,其中X∈RD×N.
2 基于核判别分析的图像集匹配
2.1 核判别分析
线性判别分析(Linear Discriminant Analysis,LDA),也称为Fisher 判别分析(Fisher Discriminant Analysis,FDA)是一种有监督的判别分析方法,其主要思想是将高维的模式样本投影到最佳鉴别矢量空间,以达到抽取分类信息和压缩特征空间维数的效果.它能够保证投影后模式样本在新的空间中有最小的类内距离和最大的类间距离,即模式在该空间中有最佳的可分离性.LDA 被广泛的应用,但是LDA 没有包含高阶的统计量,无法很好地对非线性分布的数据进行分类.
核技巧是处理非线性数据的有效方法之一,KFDA 是核函数和线性判别分析相结合的产物,它能有效地对非线性分布的数据进行分类,首先通过一个非线性映射函数φ:RD→F,将RD空间中的原始训练样本变换到某一高维的特征空间(可能是无线维的)以获得数据分布的更加丰富的表示,然后在特征空间中执行线性判别分析,找出使类间散度最大而类内散度最小的投影方向进行分类.
一般地,非线性映射通过核函数内积运算来完成:
k(Xi,Xj)=〈φ(Xi),φ(Xj)〉,

核判别分析求解最优化以下目标函数:

其中核矩阵K=[kij],kij=k(Xi,Xj),α=[α1,…,αN]T.
通过求解异特征值问题:KWKα=λKα,保留最大的C-1 个特征值对应的特征向量得到投影矩阵A=[α1,…,αC-1],其中每一个特征向量α 给定特征空间F 中的一个鉴别方向.
测试时,给定输入空间的一个图像集合的特征向量矩阵Xt∈RD,在判别子空间的C-1 维投影可以通过公式Zt=ATKt得到,其中Kt=[k(X1,Xt),…,k(XN,Xt)]T.
2.2 核函数的选择
在KFDA 中,核函数的选择直接影响到分类效果.理论上要求选择的核函数需要只要满足Mercer 条件即可,但不同核函数分类器的性能完全不同.较常用的核函数有:线性核函数、多项式核函数、高斯径向基核函数等.本文结合图像集合的协方差模型表示这一特定的条件选择核函数,充分利用协方差矩阵的正对称性简化核矩阵的计算.
给定一个矩阵,每一个列为一张图像的特征向量,X 为其协方差矩阵,设X=U∑UT表示正定对称矩阵X 的特征值分解.为了快速计算log(X),记log(∑)表示特征值的对数构成的对角矩阵,那么log(X)的计算可分解为:log(X)=Ulog(∑)UT,它仍然是一个对称矩阵[16].
记‖XF‖表示Frobenius 矩阵内积〈·〉F导出的Frobenius 范数(简称F-范数),

可以通过该范数来定义两个协方差矩阵之间的Log-Euclidean 距离[17]:
d(Xi,Xj)=‖log(Xi)-log(Xj)‖F,
度量函数d(·,·)是黎曼流形上的几何距离度量[17].该度量可以理解为存在映射φ 将黎曼流形上的点投影到欧式空间:
φ:M →TI,X →log(X),
映射φ 将黎曼流形上的点X 投影到单位矩阵I所对应的点的切空间TI,这个空间是由对称矩阵构成的向量空间.通过这个度量函数两个协方差矩阵的相似性度量转换为一般的欧式空间中的度量,因此可以直接利用欧式空间中的判别分析方法进行分类.
通过计算切空间TI中的内积,可以得到黎曼流形M 上的黎曼核[16],对∀Xi,Xj∈M,定义核函数:
k(Xi,Xj)=tr[log(Xi)·log(Xj)],
一方面,对∀X1,…,Xn∈M 与b1,…,bn∈R,因为

所以该核函数是正定的,其中tr 表示求矩阵的迹.另一方面,因为log(Xi)与log(Xj)是对称矩阵,tr[A·B]=tr[B·A],可以得到
tr[log(Xi)·log(Xj)]=tr[log(Xi)T·log(Xj)]=tr[log(Xj)·log(Xi)T]=tr[log(Xj)·log(Xi)].
所以,klog是一个实对称函数:klog(Xi,Xj)=klog(Xj,Xi).式中tr 表示求矩阵的迹,(·)T表示矩阵转置操作.因此,这个核函数满足Mercer 条件.
3 仿真实验
本节讨论在ETH80 对象分类数据库上进行基于集合的对象匹配和在加利福尼亚大学圣迭戈分校脸部追踪视频数据库(HondaUCSD Video Database)上执行基于集合的人脸识别实验.所有的实验都使用最近邻分类器进行分类.

图1 ETH80 对象数据库中的样本Fig.1 Simples from ETH80 object database
3.1 数据库
如图1(a)所示,ETH80 数据库包含苹果、小汽车、牛、杯子、狗、马、梨和西红柿8 类对象的不同视角和实例的静态图像.如图1(b)所示,每个类别包含10 个不同的实例.每个实例包含不同视角下的41 张图片.
实验中,将每一个体全部41 张图像合成为一个图像集合,整个数据库包含80 个图像集合,每个类别有10 个图像集合.测试中,将每一个体的10 个集合随机地划分为两组,每组5 个集合,分别用于训练和和测试.实验中,从集合的41 张图像中随机选择30 个视角的图像用于构造随机实验.

图2 HondaUCSD 数据库人脸检测结果示意图Fig.2 Face detected results on HondaUCSD database
HondaUCSD 数据库的视频在室内录制,包含人的不同姿态和表情变化,是一个用于做人脸识别跟踪/识别的标准视频数据库,共包含19 个人的59 段视频,每个人有2~3 段独立录制的视频.该数据库每个视频包含300~500 帧,且被分割成多个视频片段,每个片段包含大约60 帧.本文采用Viola[18]检测算子从每一帧中检测人脸组件.图2 给出了检测到的人脸示意图.实验中,每个人选择一段视频做训练,其余的视频做测试.每次随机实验,从视频中随机选择30 帧构成测试图像集.
3.2 算法比较
本文与在第1 节中提到的另外5 种基于集合的匹配方法进行了对比.这些方法包括:MSM[4],MMD[9],MDA[11],AHISD[12]和SANP[13].
比较实验基于原始文献公布的Matlab 代码实现的算法,适当调节算法的参数取最优的结果.在MSM 和MMD 算法中,使用主成份分析方法获得子空间,PCA 比率参数设置为0.95.MMD 和MDA 方法采用原始文献的参数设置,欧式距离与几何距离比值设置为2.0,邻域大小设置为默认值12.本文使用AHISD 的线性版本,SANP 算法使用文献相同的参数设置求解凸优化问题.
表1 列出了ETH80 数据库上各种算法识别率的均值和方差.实验结果显示,在ETH80 数据库上,MSM,MMD,MDA,AHISD 和SANP 算法取得基本一致的结果,在本文设定的实验条件下,本文的算法结果优于其他几个算法,平均识别率达到96%.这可能与本文采用协方差矩阵对图像的特征矩阵进行建模有关,图像特征矩阵的协方差矩阵考虑到了特征向量的二阶特征,并且考虑了图像集的整体相关性,因此能够有效地消除单张图像特征不稳定对识别结果的影响,提高了图像集合模型的稳定性.图3 给出了5 次随机实验的识别率的对比.如图3所示,每一次随机实验中,本文提出的方法都稳定地高于其他算法.

表1 ETH80 数据库上的实验结果Tab.1 Experimental results on ETH80 database
ETH80 数据库每类物体仅仅包含41 张图像,实验中我们从这41 张图像中随机选择30 张构成图像子集,虽然这些图像是从不同视角拍摄,但是它们是离散的,不能很好地满足MDA 和MMD 等算法中的流形分布假设,从另一个侧面也说明了本文采用的协方差模型能够弥补这种缺陷.另外SANP 和AHISD 两个算法都是基于近邻比较的方法,图像集合中被比较的图像由于视角的不匹配或者缺失严重地影响识别结果.
表2 列出了HondaUCSD 数据库上各种算法识别率的均值、方差.实验结果显示,本文提出方法识别率达到了95.90%,仅次于SANP 算法,但是高于其他经典的算法,进一步验证了本文提出的算法能达到较好的识别效果.图4 给出了这5 次随机实验的识别率的对比.

表2 HondaUCSD 数据库上的实验结果Tab.2 Experimental results on HondaUSCD database
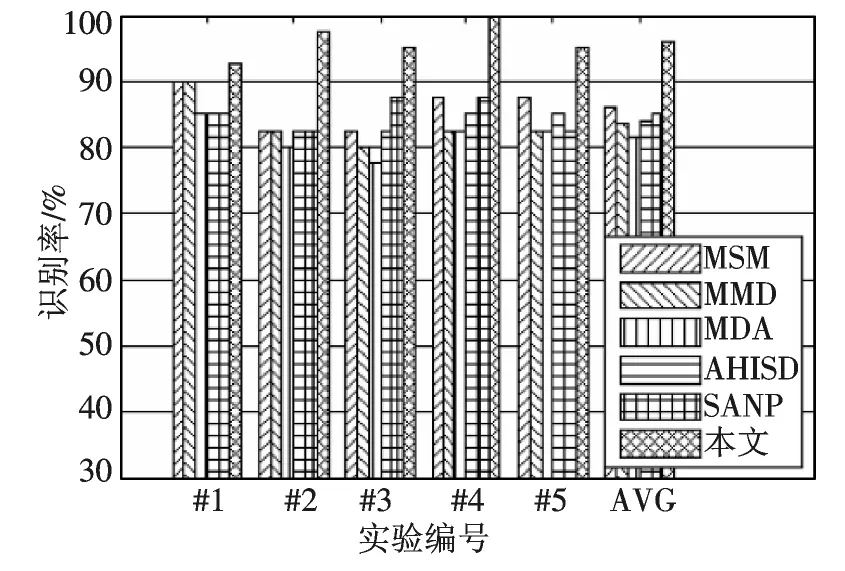
图3 ETH80 数据库实验的结果对比Fig.3 Experimental results of tested method on ETH80 database
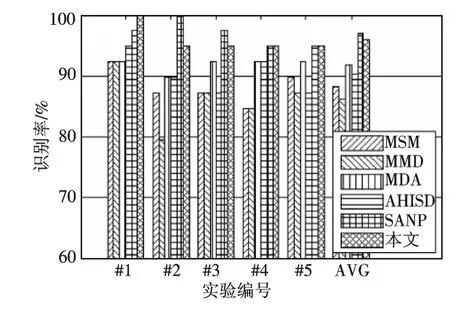
图4 HondaUCSD 数据库实验的结果对比Fig.4 Experimental results of tested method on HondaUSCD database
4 结论
图像集合匹配中的核心问题是如何对图像集合建模并比较两个模型的相似性,本文通过计算图像集合中单张图像的特征向量构成的协方差矩阵来建立图像集合的协方差表差,该方法充分利用了协方差矩阵能够提取集合中所有元素的二阶特征,因而可以获得比一阶特征更好的描述能力.
比较两个集合,可以考虑将图像集合嵌入到黎曼流形,把图像集表示成流形上的一个点.本文利用了协方差矩阵是对称正定的特征,而对称正定矩阵张成黎曼流形的子空间,从而实现将一个图像集合表示成黎曼流形上的点.传统的基于欧式度量的学习算法不能直接用于流形上点的分类,本文为解决这个问题通过计算矩阵的对数,构造一个黎曼核,从而把黎曼流形上的点的匹配投影到欧几里德空间,进而使用经典的KFDA方法进行分类.本文的图像集合建模方法有效地解决了将非欧式空间的度量转换为欧式空间的度量,从而可以结合欧式空间已有的分类方法实现分类,后续将进一步结合图模型做深入的研究.
[1]王科俊,段胜利,冯伟兴,等.单训练样本人脸识别技术综述[J].模式识别与人工智能,2008,21(5):635-642.
[2]严 严,章毓晋.基于视频的人脸识别研究进展[J].计算机学报,2009,32(5):878-886.
[3]BARR J R,BOWYER K W,FLYNN P J,et al.Face recognition from video:a review[J].Int J Patt Recog Artif Intell,2012,26(5).
[4]YAMAGUCHI O,FUKUI K,MAEDA K I.Face recognition using temporal image sequence[C]//3rd International Conference on Face & Gesture Recognition(FG '98).Nara,Japan:IEEE Computer Society,1998:318-323.
[5]ZENG Q S,LAI J H,WANG C D.Multi-local model image set matching based on domain description[J].Patt Recog,2014,47(2):694-704.
[6]曾青松.黎曼流形上的保局投影在图像集匹配中的应用[J].中国图象图形学报,2014,19(3):414-420.
[7]吕 煊,王志成,赵卫东,等.一种基于低秩描述的图像集分类方法[J].同济大学学报:自然科学版,2013,41(2):271-276.
[8]章毓晋,程正东,谭华春.基于子空间的人脸识别[M].北京:清华大学出版社,2009.
[9]WANG R P,SHAN S G,CHEN X L,et al.Manifold-manifold distance with application to face recognition based on image set[C]//Proceedings of IEEE Conference on Computer Vision and Pattern Recognition.Anchorage,Alaska,USA:IEEE,2008.
[10]WANG R,SHAN S,CHEN X,et al.Maximal linear embedding for dimensionality reduction[J].IEEE Trans Patt Anal Machine Intell,2011,33(9):1776-1792.
[11]WANG R P,CHEN X L.Manifold discriminant analysis[C]//Proceedings of IEEE Conference on Computer Vision and Pattern Recognit.Miami,Florida,USA:IEEE,2009.
[12]CEVIKALP H,TRIGGS B.Face recognition based on image sets[C]//Proceedings of IEEE Conference on Computer Vision and Pattern Recognition.San Francisco,CA,USA:IEEE Computer Society,2010.
[13]HU Y,MIAN A S,OWENS R.Face recognition using sparse approximated nearest points between image sets[J].IEEE Trans Pattern Anal Machine Intell,2012,34(10):1992-2004.
[14]BAUDAT G,ANOUAR F.Generalized discriminant analysis using a kernel approach[J].Neural Comput,2000,12(10):2385-2404.
[15]AHONEN T,HADID A,PIETIKAINEN M.Face description with local binary patterns:application to face recognition[J].IEEE Trans Patt Anal Machine Intell,2006,28(12):2037-2041.
[16]WANG R,GUO H,DAVIS L S,et al.Covariance discriminative learning:a natural and efficient approach to image set classification[C]//Proceedings of IEEE Conference on Computer Vision and Pattern Recognition.Providence,RI,USA:IEEE,2012.
[17]ARSIGNY V,FILLARD P,PENNEC X,et al.Geometric means in a novel vector space structure on symmetric positive-definite matrices[J].SIAM Matrix Anal Appl,2007,29(1):328-347.
[18]VIOLA P,JONES M J.Robust real-time face detection[J].Int J Comput Vision,2004,57(2):137-154.
