分·式·探·索·题·赏·析

□李庆社

分·式·探·索·题·赏·析

□李庆社

近年来，有关分式问题的创新题目百花齐放，令人目不暇接.它的背景更丰富、更贴近学生的生活实际.为帮助同学们熟悉新题型，迎接新挑战，特选择分式探索题加以剖析，供大家参考.

例（新疆生产建设兵团）探索问题：

（1）请你写出五个正的真分数，____，____，____，____，____，给每个分数的分子和分母加上同一个正数得到五个新分数：____，____，____，____，____.

（2）比较原来每个分数与对应新分数的大小，可以得出下面的结论：

（3）请你用文字叙述（2）中结论的含义：________.

（4）你能用图形或推理说明这个结论吗？________.

（5）解决问题：如图1，有一个长宽不等的长方形绿地，现给绿地四周铺一条宽相等的路，问原来的长方形与现在铺过小路后的长方形是否相似？为什么？

（6）这个结论可以解释生活中的许多现象，解决许多生活与数学中的问题.请你再提出一个类似的数学问题，或举出一个生活中与此结论的相关例子.

分析：本题首先通过举例、比较、观察、猜想等手段，找到不变量和变量及它们的关系，进行合理推理，得到初步结论，进而举例验证，体现数形结合思想，并运用学生已有知识解决简单的数学问题，符合同学们现有认知水平.解答：（1）答案略.（3）给一个正的真分数的分子、分母同加一个正数，得到的新分数大于原来的分数.

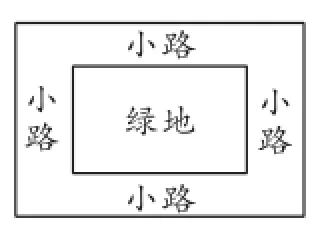
图1

（4）思路1：如图2所示，由a＜b，得s＋s1＞s＋s2，即ab＋bm＞ab＋am，a（b＋m）＝b（a＋m），可推出

图2

（5）不相似.因为两个长方形长与宽的比值不相等.

（6）数学问题举例：

②a、b不是正数，或不全是正数，情况如何？

点评：本题涉及的数学思想方法有字母代替数、由特殊到一般、化归、数形结合、数学建模等，数学思想方法是数学的“灵魂”，是分析问题、解决问题的“金钥匙”.同学们只有平时熟练地掌握这些思想方法，分析和解决问题时才能得心应手.