风电场稳态等值建模研究
2015-12-22陶力赵威
陶力,赵威
(云南电网有限责任公司昆明供电局,昆明 650200)
风电场稳态等值建模研究
陶力,赵威
(云南电网有限责任公司昆明供电局,昆明 650200)
为适应含风电场的电力系统稳态分析的需要,建立了风电场的稳态等值模型。主要就等值过程中的等效风速的求取,集电系统的等值以及潮流计算中风电节点的处理这三个方面的内容进行了研究分析。通过算例分析,证实所建的稳态等值模型精确可靠,能准确描述风电场的运行特性。
风电场;等值建模;等效风速;潮流计算
0 前言
风力发电作为目前仅次于水力发电的发展最迅速,前景最好的可再生能源发电方式,目前已经得到全球各国的大力支持[1-2]。
但由于风力发电具有出力随机,波动等不可控性,风力发电接入电力系统时会对系统的安全稳定运行带来一定的影响。风电并网对系统的影响已经成为制约其发展的重要因素。因此详细分析其并网影响,并因此来制定相应的策略减小其影响是目前国内外专家,以及新能源公司研发机构的研究重点[3]。
潮流计算是电力系统最常用的分析之一,研究含风电系统的稳态分析时,需要建立能够准确描述风电场特性的风电场稳态模型[4]。在稳态等值中,本文将风电场等值成一台风电机组,主要从以下三个方面对其进行了研究:
1)风电场等值机等效风速计算;
2)风电场集电网络等值计算;
3)风电节点潮流计算模型研究。并通过算例分析证明本文所提出的风电场稳态等值模型计算准确可靠。
1 风电场等效风速计算
1.1 风电场风速模拟
风电场的尾流效应是指在风电场中,各台风机由于排列位置的不同,风向后方风机输入风速受前方风机的影响,使不同风机具有不同的输入风速。Jensen模型能较好的模拟尾流效应,其原理如图1所示。

图1 Jensen尾流效应模型
图中,X为风机间距,R为叶轮半径,Rw为尾流半径,v0和vx为考虑尾流效应时,吹入和离开的风速。
则考虑尾流效应的风速由式 (1)表示:

式中,Ct为风机的推力系数。
1.2 等效风速计算
将整个风电场等值成为一台风机时,该等值机的输入风速如何确定将是等值时首先要解决的问题[5-6]。根据能源传输过程中,总能源守恒的原则,忽略风机内部的损耗,可认为风电机输出功率等于风力机捕获的风能,每一台风力机捕获的风能可由式 (2)求取

式中,Pi为第i台风电机输出功率,Cpi为第i台机组风能利用系数,ρ为空气密度,A为风电机组叶轮扫风面积,vi为第i台机组的风速。
风电机组输出功率之和P∑可由式 (3)表示:
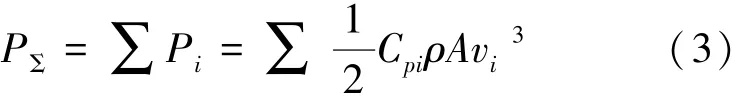
将所有机组等值成一台机组,其叶轮扫风面积为场内所有机组叶轮扫风面积之和nA,机组的等效风速为vequ,等效风能利用系数为Cp.equ,则风电机组输出功率之和P∑可表示成式 (4):

等效风能利用系数的计算采用式 (5):

由式 (3)和式 (4)可得到等效风速的计算公式 (6):
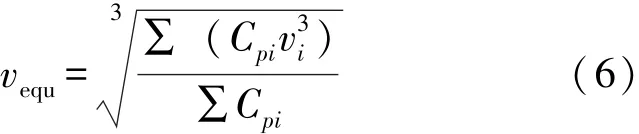
得到了等效风速vequ就可直接应用式 (2)来得到整个风电场的输出功率。
2 风电场集电系统等值
对含风电系统进行稳态分析时,风电场内部的集电系统对系统的潮流影响较大,若忽略这部分的影响则可能导致计算结果和实际误差较大[7-8]。对于典型的风电场,集电系统系统主要包括每台风机对应的单元变压器,由汇流母线构成的集电线路以及风电场的主变压器。本文对风电场集电网路的等值也分这三部分分别进行等值建模。
2.1 单元变压器的等值
单元变压器是接到风电机组的出口处的小型升压变压器,它的一端接风电机组,另一端接集电线路。单元变压器的等值模型可直接通过n台变压器的并联得到,即ZT-equ=ZT1‖…‖ZTn。目前,对于同一风电场,单元变压器的型号一般相同。因此,等值后的单元变压器参数可以由式(7)计算得到:

2.2 集电线路的等值
风电场由于占地面积较大,各个风机之间距离相对较远,因此其内部集电线路规模大,对风电场并网特性的影响不容忽略。为保证风电场等值前后潮流计算结果不变,需使等值前后集电系统损耗相等。根据集电线路的种类,可将对其的等值分为电缆线路等值和架空线路等值,其相应的等值电路如图2所示:
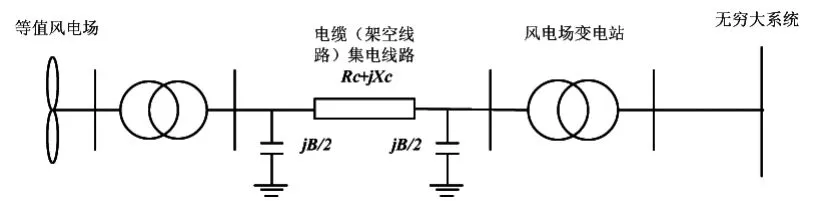
图2 集电线路等值电路
其中,RC+jXC为集电线路的等值阻抗,B为电缆充电电容。
电缆线路和架空线路两者最大的区别在于,电缆线路的充电电容远大于架空线路,因此电缆线路等值时必须考虑充电电容的影响,而架空线路的充电电容很小,等值时可以忽略其影响。
假设风电机组功率因数和机端电压相同。线路的损耗可由式 (8)得到:
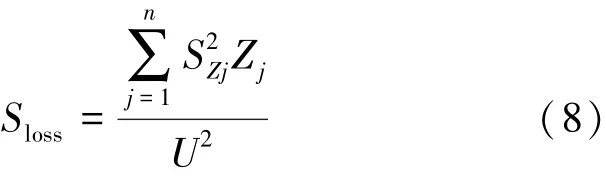
利用等值前后总损耗不变的原则,可知等值阻抗为式 (9)所示:

对于电缆线路的等值,根据等值前后无功功率守恒,线路等值后的电纳如式 (10)所示

综上,集电线路的等值电路中,等值阻抗RC+jXC可由式 (9)求得,充电电容B可由式(10)求得。
2.3 主变压器的等值
风电场若通过一台主变并网,因此该变压器在等值时可以保留;若风电场通过几台主变并网,则可根据主变并联的接入方式,等值时根据电路并联的关系来确定其等值参数。
3 风电场节点潮流计算模型研究
传统潮流计算时,将电力系统中的节点分为PV节点、PQ节点以及平衡节点3种类型。风电并网后,由于其出力的特殊性,将其等效为何种类型的节点参与潮流计算一直是国内外专家的研究重点。通过研究发现,风电场作为何种节点类型处理需要根据风电场风机的类型、控制方式来确定[9-10]。风电场的典型节点类型包括PQ模型、PV模型以及RX模型这三类,本文将分别进行讨论分析。
3.1 PQ模型
将风电场作为PQ节点进行潮流计算是最早的处理方法,针对以异步风力发电机为主的风电场或双馈和直驱风机采用恒功率因数并网控制模式时,一般将风电场等值成PQ节点。风电节点的有功功率由风速决定,可由式 (11)计算得到:

式中,P为风电机组输出功率,Cp为机组风能利用系数,ρ为空气密度,A为风电机组叶轮扫风面积,v为风速。
风电场的功率因数恒定不变,则风电节点的无功功率由式 (12)计算得到:

式中,φ为功率因数角。
3.2 PV模型
双馈异步风力发电机和直驱永磁同步风力发电机可以实现恒电压控制。若风电场所有或部分风机都采用恒电压控制方式并网运行,则风电场可看作PV节点。但由于风电场内风机的无功可调节量一般较小,针对电压波动较大,无功需求较多或风电场中采用恒电压控制的风机数目较少的情况,风电场的无功支撑能力不足。此时在将该风电场看作PV转PQ节点时,需要设置无功容量的限值。
风电节点的有功功率由风速决定,可由式(11)计算得到,节点电压直接被控制到一个值。无功容量的限值由式 (13)决定。

式中,n为风电场中采用恒电压控制的机组数目,若风机全部采用该控制方式,则该值等于风电场内风机开机数。
3.3 RX模型
对于全由异步风力发电机组成的风电场,有文献提出了RX模型。该模型将异步风力发电机作为组抗型的负荷加入潮流计算的雅克比矩阵中。运行该模型计算潮流时,分为两步迭代完成,除了常规潮流的迭代计算以外还有发电机内部的滑差迭代。
4 算例分析
为了验证以上等值模型的正确性,本文构造了一个风电场。
风电场共有10台风机,总容量为10×1500 kW,每台风机通过一个单元变压器接到架空线(型号为LGJ—35,几何均距为1.0 m)上,形成两个风电机组。1至5号风机为一组,6至10号风机为另一组。两组风电机组分别通过架空线(型号为LGJ—95,几何均距为2.0 m)连接到主变压器上,主变压器的另一端连接系统;风电机叶轮扫风面积为1 840 m2,额定电压为690 V,异步机定子阻抗为0.004 53+j0.050 7 Ω,转子阻抗为0.004 86+j0.149 1 Ω,励磁电抗为j2.205 9 Ω。
单元变压器的型号为S9-630/35,阻抗值为0.009 9+j0.049 1 Ω;主变压器选用12500 kVA双绕组低压侧为35kV级无励磁调压变压器,阻抗值为5.730 6+j101.64 Ω.
型号为LGJ-35的架空线的电阻为0.85 Ω/ km,电抗为0.366 Ω/km;型号为LGJ-95的架空线的电阻为0.33 Ω/km,电抗为0.371 Ω/km;同一组中,两台相连接的风机之间的架空线的长度为120 m,将一组风电机组连接到主变压器的架空线的长度为600 m。
4.1 风电场详细模型的稳态计算
风电场内部风机的输入风速考虑尾流效应,第一排的风速取为 15 m/s,Ct取0.2,根据式(1)可计算得到每台风电机处的风速如表1所示。

表1 每台风机处的风速 (m/s)
6至10 号的风机风速和表1中第1至5号风机的风速相同。
假定每台风机的尖速比如表2所示。
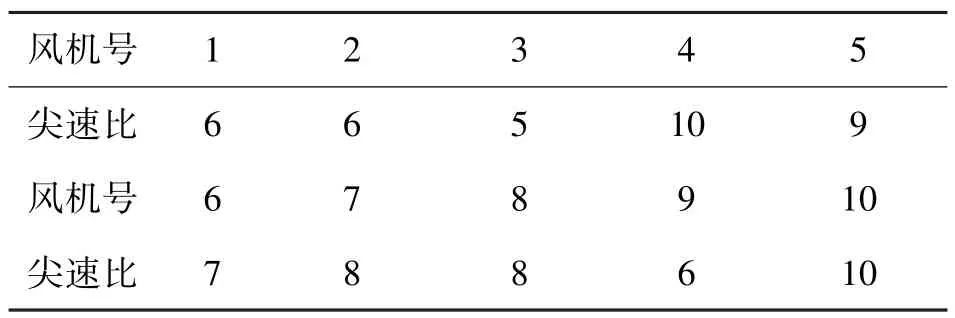
表2 每台风机的尖速比
根据风能利用系数与尖速比的关系,可计算得到每台风机的风能利用系数如表3.5所示。

表3 每台风机的风能利用系数Cp
假设每台风机的功率因素相等,都为cosφ= 0.95,则利用式 (11)和 (12)可以计算得到每台风机的输出功率。
电力系统中功率损耗的计算公式如式 (14)所示

根据式 (14)可计算出每台风机的单位变压器、集电系统线路、以及主变压器的功率损耗。从而计算得到整个风电场出口处的输出功率为:
P+jQ=11.971 0-j7.4055(MVA)
4.2 风电场等值模型的稳态计算
风电场等值模型如图3所示:
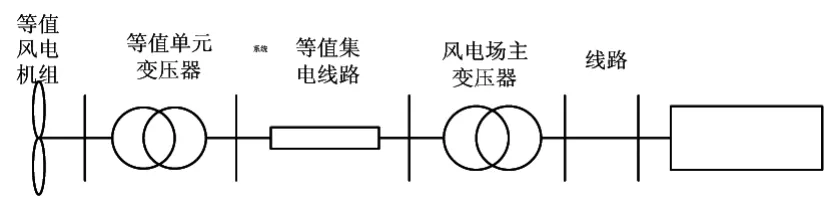
图3 风电场等值电路图
由表3和式 (5)得到等效风能利用系数为:

又由式 (6)得到等效风速为:
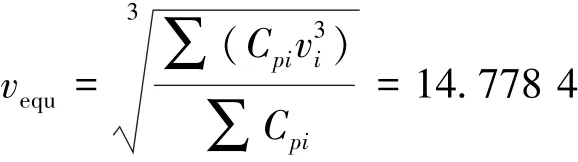
等值风电机组出口处的有功功率根据式 (4)计算得到:

假设风电的风电机组按恒功率因素控制方式控制,功率因素为-0.95.则等值机出口处的无功功率为:
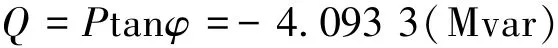
由式 (7)和式 (9)得到等值单元变压器和等值集电线路的阻抗为:
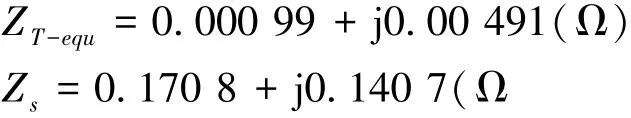
分别根据式 (14)计算得到单元变压器、集电系统以及主变压器的功率损耗,从而得到整个等值风电场出口处的输出功率为:

等值前后的风电场输出功率近似相等,从而可以证实等值模型精确有效。
4.3 风电场潮流计算模型分析
将此风电场通过线路接入IEEE-30节点标准测试系统的30号节点,如图4所示。

图4 风电场接入IEEE-30节点系统图
分别将风电场作为PQ节点、PV节点以及RX模型接入系统进行潮流计算。
4.3.1 PQ模型
将整个等值后的风电场按PQ节点接入IEEE -30节点标准测试系统的30号节点,其输入功率为上文计算得到的功率。在Matlab上运用牛顿-拉夫逊法编程计算得到接入点 (30号节点)处的电压114.257 kV,输出功率为11.99-j7.32 MV· A,迭代次数为8次。
4.3.2 PV等值模型的计算
将整个等值后的风电场按PV节点接入IEEE -30节点标准测试系统的30号节点,其输入有功功率为上文计算得到的有功功率。电压控制为112 kV。在Matlab上编程计算得到接入点 (14号节点)处的输出无功功率为-8.26 Mvar,迭代次数为8次。
4.3.3 RX等值模型的计算
根据3.1.3.3节介绍的风电场RX等值模型的计算方法,将此风电场RX等值模型通过线路接入IEEE-30节点标准测试系统的30号节点,在Matlab上编程计算得到接入点 (30号节点)处的电压为 113.476 kV,输出的有功功率为12.08 MW,迭代次数为17次。
5 结束语
本文主要就风电场的稳态等值建模问题进行研究分析。针对建模过程中的等效风速求取、集电系统等值方法以及风电节点潮流计算时的处理方法这三个方面进行了深入的分析。得到了以下结论:
1)本文所建立的风电场稳态等值模型和详细模型计算结果近似相同,证明所建模型精确可靠。
2)风电场稳态等值建模中不能忽略集电系统的影响。
3)潮流计算中风电节点的处理方法要根据风机类型以及其控制方式来决定。
[1] 刘开俊.风电并网对电网的影响分析及解决方案 [J].中国电力,2012,45(9):7-10.
[2] 袁小明.大规模风电并网问题基本框架 [J].电力科学与技术学报,2012,27(1):16-18.
[3] 胡明.阿尔伯塔风电并网对系统运行的影响和对策 [J].电力技术经济,2009,21(2):16-20.
[4] 曹娜,赵海翔,陈默子,等.潮流计算中风电场的等值[J].电网技术,2006,30(9):53-56.
[5] 李洪美,万秋兰,向昌明.考虑风速的风电场等值方法[J].电力自动化设备,2013,33(1):121-123.
[6] 严干贵,李鸿博,等.基于等效风速的风电场等值建模[J].东北电力大学学报,2011,31(3):13-19.
[7] 高晶,蔡旭,曹云峰.计及集电线路和内部损耗的风电场模型分析比较 [J].电网与清洁能源,2011,27(3):60 -63.
[8] 孙勇,李海峰,等.风电场静态等值及应用研究 [J].江苏电机工程 [J].2012,31(4):52-54.
[9] 游晓科,胡婷,等.电力系统潮流计算中的风电场模型研究现状及展望 [J].电工电气,2012(10):1-4.
[10] 王皓怀,汤涌,等.潮流计算和机电暂态仿真中风光储联合发电系统的实用等值方法 [J].中国电机工程学报,2012,32(1):1-8.
Research on Steady-state Equivalent Modeling of Wind Farm
TAO Li,ZHAO Wei
(Kunming Power Supply Bureau,Yunnan Power Grid Co.,Ltd.,Kunming 650200,China)
In order to analysis the operation of the power system with wind farm connected.A steady-state model of wind farm is necessary.This paper gave three aspects which are to obtain equivalent wind,the equivalent of collection system,and the wind generation field nodes in load flow calculation.Finally,in simulation,the steady-state model which is used to describe the operating Characteristics of wind farm is efficacious and accurate.
wind farm;equivalent modeling;equivalent wind;load flow
TM73
B
1006-7345(2015)05-0065-05
2015-04-22
陶力 (1987),男,云南电网有限责任公司昆明供电局,长期从事电网运行维护方面的研究 (e-mail)45759651@qq.com。
赵威 (1987),男,硕士,云南电网有限责任公司昆明供电局,长期从事高电压绝缘技术方面的研究 (e-mail)569452381@qq.com。
