一种新型多温区恒温箱均温性的数值模拟与实验验证
2015-12-22赵秀红刘宝林
赵秀红 刘宝林
(上海理工大学生物系统热科学研究所 上海 200093)
一种新型多温区恒温箱均温性的数值模拟与实验验证
赵秀红 刘宝林
(上海理工大学生物系统热科学研究所 上海 200093)
本文针对自行设计的一种新型的具有三个箱体的多温区恒温箱进行其均温性的研究。以多温区恒温箱的一个箱体为研究对象,建立了三维稳态数值模型,模拟了加热器情况不同时该箱体内的温度分布。结果表明,采用方形薄片加热器并布置于风机下方时,该箱体内的温度场最均匀。恒温箱三个箱体的加热器均采用上述情况后,对其设定了工况1(各箱体的设定温度分别为-15℃,-10℃,-5℃)和工况2(各箱体的设定温度分别为-20℃,-15℃,-10℃)进行实验。结果显示,工况1(即模拟工况)下的模拟值与实测值较吻合,最大误差为3.1%;两种工况下各箱体的温度均匀度最大为0.54℃。结果表明,在不同的测试工况下该多温区恒温箱各箱体内的温度分布都能维持均匀。
多温区;恒温箱;温度场;温度均匀度;FLUENT模拟
恒温箱已日益成为样本储存、实验中必不可少的提供恒温环境的设备。不同种类的样本如果蔬、肉类、生物试剂、疫苗等都有各自最佳的储存温度,且对于同一种样本往往需要进行多种温度下的性能实验,所以多温区恒温箱具有实际需求。目前对于恒温箱的研究无论是结构方面还是控制方面,多数是针对单个温区进行的。如穆江勃等[1]研制了一台基于半导体制冷的医用恒温箱,体积为8 L,温度维持在2~6℃,用于储存血液;张敏等[2]设计了一台蒸气压缩式制冷的恒温箱,控温精度达到±0.5℃,并提出系统加储液器有利于提高控温精度;叶庆银等[3]分析了恒温箱结构特性对恒温性能的影响,提出较大的体型系数有利于维持恒温;屈百达等[4]考虑了温度检测滞后的情况对一台电热恒温箱引入H无穷控制方法优化了控制系统。
对于多温区恒温箱的研究目前还鲜有文献报道。多温区恒温箱能同时提供多个不同温度的恒温环境,可以满足样本多样化储存温度的需求,并能实现多种温度下性能实验的同时进行,节省实验时间,提高效率。本文针对自行研制的一台多温区恒温箱,进行其均温性的研究。采用FLUENT软件模拟箱体内的温度场,为恒温箱选择合适的加热器及布置位置以实现温度场的最优化,并用实验验证了模型的准确性及各温区具有较好的均温性。
1 计算模型的建立
自行设计的多温区恒温箱设0~-10℃,-10~-15℃和-15~-25℃三个温区。系统原理如图1所示,恒温箱采用蒸气压缩方式制冷,电加热方式制热,通过冷热量的匹配实现恒温,控温精度可达±0.4℃。各温区的制冷管路并联,共用一台压缩机和一个冷凝器。每个温区内装设一台轴流风机,加强空气与蒸发器和电加热器的换热,使箱体内的温度均匀。
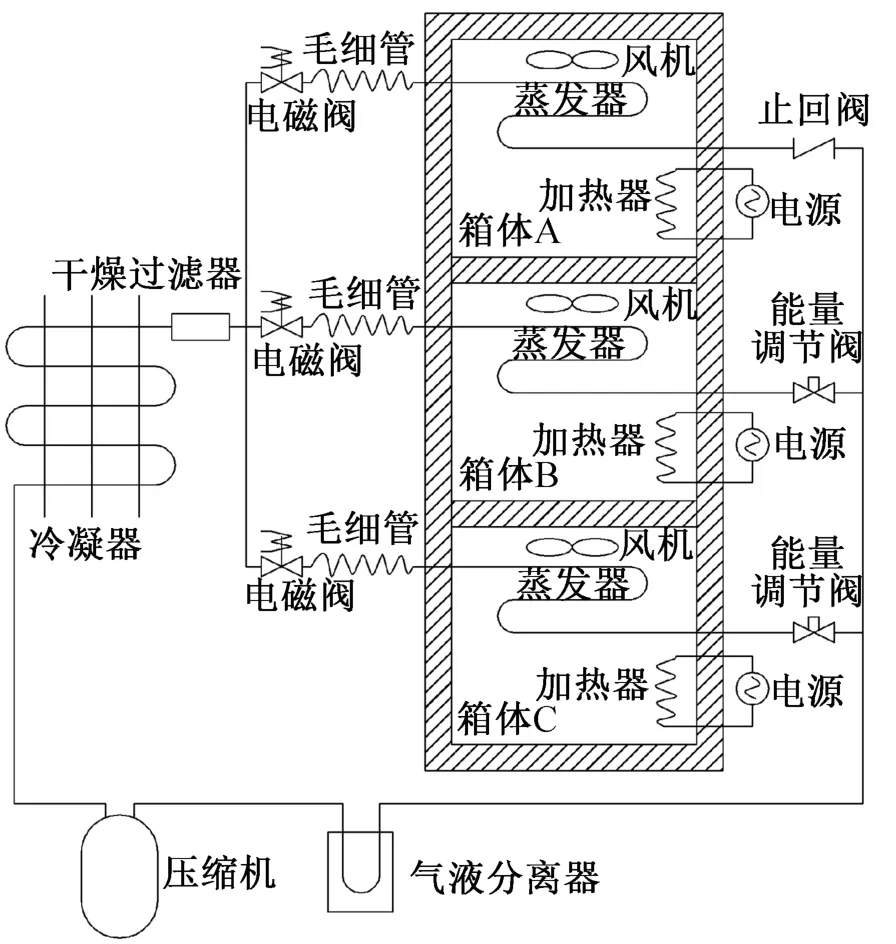
图1 多温区恒温箱系统原理示意图Fig·1 SchematiCdiagramof themultitemperature thermostat
1·1 物理模型
本数值模拟以上述多温区恒温箱的箱体B为研究对象。恒温箱各箱体结构、尺寸均相同(如图2)。蒸发器固定于箱体后壁面上。综合考虑了箱体内的气流组织及风速对样本干耗的影响,将轴流风机固定于箱体内隔板中心偏上的位置,直径为60 mm。两个回风口的尺寸相同为400 mm×25 mm。本模型以箱体隔板、上、下、左、右壁面及门所围成的空间为控制体,其尺寸长(x)×宽(y)×高(z)为:300 mm×400 mm×350 mm。其中轴流风机物理模型为一无限薄圆面[5],其圆心的xyz坐标为(-0.15,0,0.05)。
1·2 模型假设
由于物理模型自身的复杂性,在进行数值计算时做出如下假设[6-9]:
1)在稳态工况下计算模型内的温度场,因此所有微分方程中忽略时间项;

图2 单个箱体结构Fig·2 Structure diagramofAsingle chamber
2)箱体内的空气为干空气且为牛顿流体,密度及定压比热容为定值;
3)箱体内空气在固体壁面上满足无滑移条件;
4)满足Boussinesq假设,即忽略流体中粘性耗散。标准k-ε模型是典型的两方程模型。该模型稳定性高,计算量适中,有较多的数据积累和较高的精度,应用广泛。本模型中空气的流动情况满足标准kε模型的适用条件,故湍流模型采用标准k-ε模型,并在近壁面处采用标准壁面函数法进行处理。
模型中轴流风机的电机是一个内热源,因其功率很小,对整个温度场的影响非常小,予以忽略。模型中不考虑辐射换热。
1·3 控制方程
控制体内的空气流动和传热遵循质量守恒、动量守恒及能量守恒方程,并满足湍流模型中的k方程和ε方程。这一系列的基本方程可由以下统一形式的方程描述,即[10]:
式中:φ是某个变量;Γ是变量的扩散系数;S是源项。上式中各变量、扩散系数及源项见表1。
表1中:
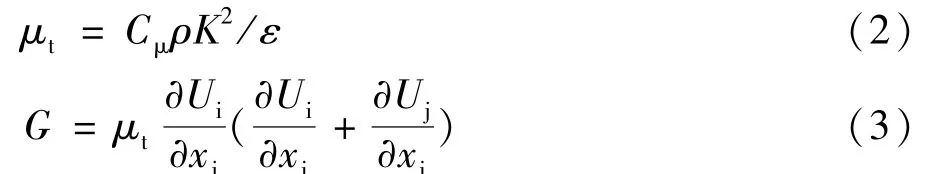
式中:Cμ=0.09;C1=1.44;C2=1.92;σT=0.95;σk=1.0;σε=1.3。
1·4 边界条件
1)壁面边界条件:恒温箱处于环境温度23℃时,对其设定工况1(箱体A、B、C的设定温度分别为-15℃,-10℃和-5℃),待各箱体内的温度达到设定值±0.4℃的范围并且稳定2 h后,通过实验台测得箱体B各内壁面及隔板的温度值作为模型的壁面边界条件为第一类边界条件。测试方法:每个面上布置三个测点,每2 min采集一次温度值,共采集15次。取其平均值作为各壁面的温度值[7]。
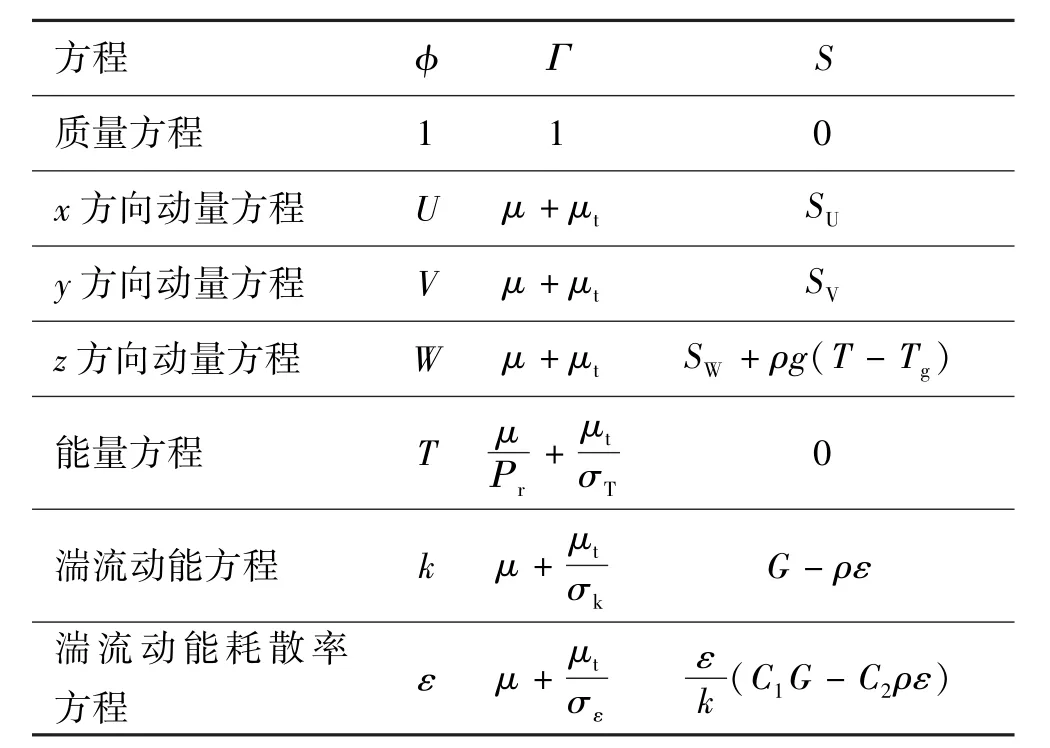
表1 各控制方程中的变量、扩散系数及源项Tab·1 Variables,diffusion coefficients and source terms of each governing equation
2)入口条件:入口设定为进气扇模型,由轴流风机参数确定压升-速度多项式函数以及周向、径向和轴向速度[5,11]。其温度值由实验测得,为第一类边界条件。实验工况同上述壁面条件获取实验。采用湍流强度与特性尺寸定义湍流。
3)出口条件:出口设置为压力出口边界条件,温度值由实验测得,为第一类边界条件。实验工况同上述壁面条件获取实验。采用湍流强度与特性尺寸定义湍流。
4)内热源条件:通过热平衡计算,给定加热器功率。按面积热源给定内热源条件为第二类边界条件。
1·5 求解设置及收敛标准
模型设定为压力-速度耦合计算并采用SIMPLE算法。压力离散采用标准格式,其他方程离散均采用二阶迎风格式。能量方程的收敛精度设为残差<10-6,其他方程的收敛精度设为残差<10-3。在各方程残差收敛到设定的精度,并且进出口流量平衡的条件下,判定解收敛。
2 实验验证
2·1 实验方法
多温区恒温箱各箱体均采用方形薄片加热器并布置于隔板上风机下方时,对其处于环境温度23℃,进行了两种工况下的测试(其中工况1箱体A、B、C的设定温度分别为-15℃,-10℃和-5℃;工况2箱体A、B、C的设定温度分别为-20℃,-15℃和-10℃)。各箱体由制冷系统冷却至基本达到设定温度后,再开启电加热器,由冷热量的均衡匹配使温度稳定在设定值±0.4℃的范围内。每个箱体内布置9个温度测点。在各箱体温度稳定2 h后,对恒温箱内测点的温度值进行采集。每2 min采集一次,共采集15次[12]。
2·2 测点布置
各箱体内的测点位置相同,如图3所示。
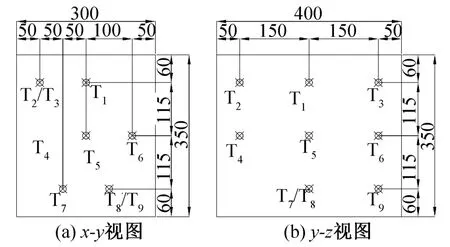
图3 测点布置图Fig·3 Layout diagramof the test points
3 结果分析
3·1 加热器形状对温度场的影响
恒温箱处于环境温度23℃,设定工况1时,对箱体B在情况Ⅰ(采用方形薄片加热器布置于隔板上,风机下方,加热器尺寸为60 mm×60 mm×2 mm,中心坐标为(-0.147,0,-0.07))和情况Ⅱ(采用棒状加热器布置于隔板上,风机下方,加热器尺寸为R=5 mm,H=80 mm,中心坐标为(-0.14,0,-0.07))时的温度场进行了稳态工况下的数值模拟。结果如图4和图5所示。
分析图4可得:由于风机送风为经蒸发器冷却的空气,温度较低,所以图4(a)中截面上部送风核心区为一面积很小的低温区。等温线以低温区为中心,呈似椭圆环分布,温度值向四周逐渐升高。截面的下部受加热器散热影响,温度比上部高,使263 K等温线上凸。总体而言,整个截面的温度场较均匀,温度在262.6~263.2 K之间,接近设定值263 K。
图4(b)截面的温度场中存在一个由风机送风形成的低温区和一个由加热器散热形成的高温区,围绕低温区和高温区等温线相对较密,其他区域温度较均匀,在262.7~263.3 K之间。
由于风机送风到达门后受限制向上、下走,所以在图4(c)中靠近门处温度较低,而在隔板处加热器上部温度较高。其他区域温度较均匀,温度值在262.8~263.2 K之间,接近设定值263 K。
将图5与图4中对应截面的温度分布进行对比可知,图5(a)的温度场除在截面中心位置存在由风机送风引起的低温区外,还存在一个局部高温区(该高温区由送风底层携带加热器上部高温空气所致),等温线分别绕低温区和高温区密集分布,造成截面中心区域温度梯度大,总体温度不均。

图4 情况Ⅰ(采用方形薄片加热器布置于风机下方)时箱体B内的温度场云图Fig·4 Temperature field in chamber B under conditionⅠ(a square-shaped heater was installed under the fan)

图5 情况Ⅱ(采用棒状加热器布置于风机下方)时箱体B内的温度场云图Fig·5 Temperature field in chamber B under conditionⅡ(a rod-shaped heater was installed under the fan)
图5(b)中,由于风机送风在下部回流区与棒状加热器换热不充分造成加热器周围等温线非常密集。且由于送风底层携带加热器上部高温空气导致温度场中心区域等温线向右凸,而截面下部由于回流空气温度较低,等温线向左凸。总体而言,图5(b)的整个温度场等温线密集,温度梯度大,均匀性比图4(b)差。图5(c)中加热器周围等温线密集,温度较高,而其他区域温度较低。分析原因为棒状加热器表面积小与周围空气换热不充分所致。其温度均匀性比图4(c)差。

图6 情况III(采用方形薄片加热器布置于风机侧方)时箱体B内的温度场云图Fig·6 Temperature field in chamber B under condition III(the square-shaped heater was installed beside the fan)
通过上述分析可得:就本文所研究的恒温箱而言,采用方形薄片加热器较棒状加热器散热面积大,相同功率下,加热器温度低,在轴流风机作用下,冷热空气掺混更充分,温度场更均匀。
3·2 加热器位置对温度场的影响
恒温箱处于环境温度23℃,设定工况1时,对箱体B在情况III(采用方形薄片加热器布置于隔板上,风机侧方,加热器尺寸为60 mm×60 mm×2 mm,中心坐标为(-0.15,0.1,0.05))时的温度场进行了稳态工况下的数值模拟。结果如图6所示。
将图6与图4中对应截面的温度分布进行对比可知:图6(a)和图4(a)的温度场很相似,都存在一个低温区,等温线以低温区为中心,呈似椭圆环分布。而图4(a)中的低温区面积相对较小,温度梯度较小,大部分区域温度更均匀。温度值更接近设定值。图6(b)截面y=0的温度场因没有剖到加热器,故没有高温区,大部分区域温度值在261.8~262.8 K之间,较设定值偏低。图6(d)截面的温度值在262.3~262.9 K之间,也较设定值偏低。
对情况III箱体B内的温度场还进行了截面y=0.1的剖切,如图6(c)所示。由其温度场可以看出,加热器周围温度很高,等温线非常密集。
综上所述,情况III(采用方形薄片加热器布置于风机侧方)时箱体B内的温度场均匀性较差,加热器周围温度较高,而大部分区域温度偏低。分析其原因为加热器所处流场位置不佳,导致其与空气换热不充分。而情况Ⅰ(采用方形薄片加热器布置于风机下方)时,加热器恰处于流场中风机送风口与下部回风口之间的回流区,冷热空气换热充分,温度场均匀。
3·3 模拟结果的实验验证
由2.1所述实验方法获得恒温箱处于环境温度23℃,工况1下,箱体B内9个测点的温度值(每一测点有15个值,取其平均值作为该点的实测值),与模拟值进行了对比,列入表2。
由表2可以看出,工况1下箱体B内各测点的温度实测值和模拟值较接近,两者绝对误差最大为0.32℃,百分比误差为3.1%。可认为模拟结果是可信的,验证了模型的准确性。因为模拟值均比实测值高,且最大差值出现在测点T1,所以分析其原因为以压升-速度多项式函数代替轴流风机特性曲线的过程中,存在一定偏差,使模型中的压升略小于风机实际的静压。
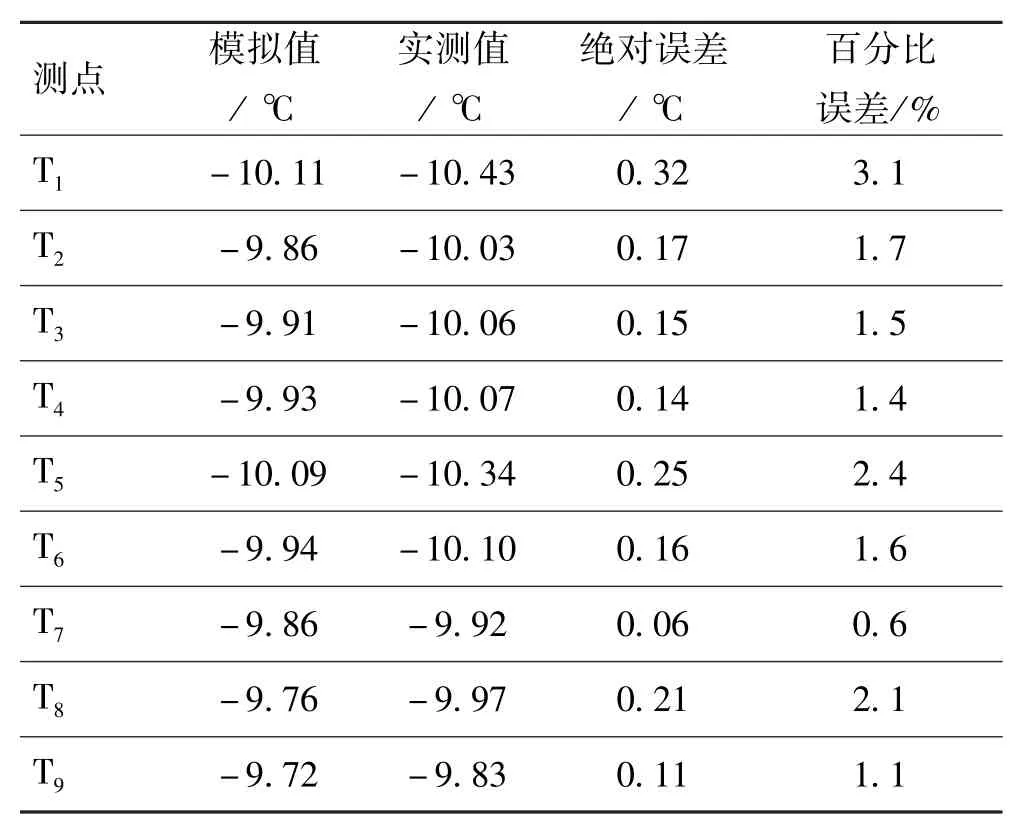
表2 工况1箱体B内温度模拟值和实测值的对比Tab·2 Comparison between simulated values and measured values in chamber B under mode 1
3·4 恒温箱各温区的均温性分析
由2.1所述实验方法获得多温区恒温箱处于环境温度23℃,设定工况1和工况2下,各箱体内测点的温度值,按以下公式计算温度均匀度[12]。计算结果列入表3。
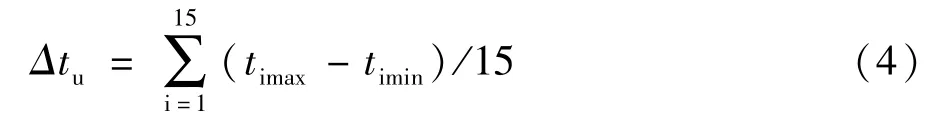
式中:Δtu为温度均匀度,℃;timax为各测点在第i次测得的最高温度,℃;timin为各测点在第i次测得的最低温度,℃。

表3 工况1和工况2情况下各箱体内的温度均匀度Tab·3 Temperature uniformity in each chamber under mode 1 and mode 2
由表3中的数据可以看出,工况2条件下箱体A内的温度均匀度最大为0.54℃,工况1条件下箱体C内的温度均匀度最小为0.38℃。其它情况下各箱体内的温度均匀度也较小。因此可以认为多温区恒温箱各温区具有较好的均温性。
4 结论
以多温区恒温箱的一个箱体为研究对象,针对加热器的不同形状和布置位置,采用FLUENT软件进行了三维稳态数值模拟。通过分析所得温度场,为多温区恒温箱选择了加热器的最佳形状和布置位置。并通过实验数据验证了模型的准确性。主要结论如下:
1)即使箱体内存在轴流风机强迫空气换热的情况下,采用棒状加热器的温度场均匀性依然较差。而方形薄片加热器表面积大,相同功率情况下,表面温度低,与箱体内空气换热更充分,不易形成局部高温区,温度场更均匀。
2)在本恒温箱中加热器布置于箱体隔板上,风机下方时,恰处于流场中风机送风口与下部回风口之间的回流区,冷热空气换热充分,温度场均匀。
3)在各箱体均采用情况Ⅰ(方形薄片加热器布置于风机下方)时,用实验数据验证了多温区恒温箱具有较好的均温性。
本文受上海市东方学者跟踪计划项目资助。(The project was supported by the Eastern Scholar Programat Shanghai High Institutions.)
[1] 穆江勃,卢菡涵,刘志奇,等.基于半导体制冷的医用恒温箱的设计研究[J].制冷,2013,32(3):86-89. (Mu Jiangbo,Lu Hanhan,Liu Zhiqi,et al.Design and research ofmedical oven based on semiconductor refrigeration[J].Refrigeration,2013,32(3):86-89.)
[2] 张敏,侯予,张兴群,等.小型制冷恒温箱的研制及试验研究[J].制冷与空调(北京),2006,6(6):69-72. (Zhang Min,Hou Yu,Zhang Xingqun,et al.The development and experimental investigation of the miniature refrigeration thermotank[J].Refrigeration and Air-conditioning(Beijing),2006,6(6):69-72.)
[3] 叶庆银,刘斌,臧润清,等.小型恒温箱恒温性能的理论及实验研究[J].制冷与空调(北京),2007,7(4): 48-50.(Ye Qingyin,Liu Bin,Zang Runqing,et al.Theoretical and experimental study on performance of small thermostat[J].Refrigeration and Air-conditioning(Beijing),2007,7(4):48-50.)
[4] 屈百达,夏怡,郑莲和.恒温箱温度的H∞优化控制[J].江南大学学报(自然科学版),2004,3(2):111-114.(Qu Baida,Xia Yi,Zheng Lianhe.A temperature control in calorstat based on H∞control[J].Journal of Jiangnan University(Natural Science Edition),2004,3 (2):111-114.)
[5] 李鹏飞,徐敏义,王飞飞.精通CFD工程仿真与案例实战[M].人民邮电出版社,2011:168-170.
[6] 徐倩,谢晶.数值模拟在多温区冷藏车领域的应用[J].制冷技术,2008(4):32-37.(Xu Qian,Xie Jing. Application of numerical simulation in the field of multitemperature refrigerated trucks[J].Refrigeration Technology,2008(4):32-37.)
[7] 傅烈虎,丛伟,李青冬.冰箱内温度场与流场数值模拟[J].制冷,2008,27(1):75-80.(Fu Liehu,Cong Wei,Li Qingdong.Numerical simulation of the temperature field and the flow field insideArefrigerator[J].Refrigeration,2008,27(1):75-80.)
[8] 俞炳丰,费继友,孟祥兆,等.间冷式冰箱冷冻室内流场的PIV测试和计算模拟[J].制冷学报,2003,24 (2):32-36.(Yu Bingfeng,Fei Jiyou,Meng Xiangzhao,et al.PIVmeasurementand numerical simulation of the inner flow field of freezer chest of frost-free refrigerator[J].Journal of Refrigeration,2003,24(2):32-36.)
[9] 吴小华,吴业正,曹小林.冰箱室内温度场和流场的仿真及结构优化[J].制冷学报,2004,25(1):36-38. (Wu Xiaohua,Wu Yezheng,Cao Xiaolin.Simulation and optimization of temperature field and flow field inside freezer[J].Journal of Refrigeration,2004,25(1):36-38.)
[10]陶文铨.数值传热学[M].西安:西安交通大学出版社,1988:431-439.
[11]H B Nahor,mL Hoang,PVerboven,etal.CFDmodel of the airflow,heat and mass transfer in cool stores[J].International Journal of Refrigeration,2005,28(3):368-380.
[12]JJF 1101—2003.环境试验设备温度、湿度校准规范[S].北京:国家质量监督检验检疫总局,2003.
About the corresponding author
Liu Baolin,male,Ph.D./professor,Institute of Biothermal Science,University of Shanghai for Science and Technology,+86 13636524955,E-mail:blliuK@163.com.Research fields:cryobiology.
Numerical Simulation and Experimental Verification of Temperature Uniformity inANovel multi-temperature Thermostat
Zhao Xiuhong Liu Baolin
(Institute of Biothermal Science,University of Shanghai for Science and Technology,Shanghai,200093,China)
In this paper,the temperature uniformity ofAself-designed novelmulti-temperature thermostatwith three chamberswas studied.A steady-state three-dimensional numericalmodel based on one chamber of the thermostatwas built to simulate its temperature distribution under different heater conditions.The results showed that themost uniformtemperature distribution was obtained under the condition that the square-shaped heater was used and installed under the fan.Then with all chambers under such heater condition,the thermostatwas tested undermode 1(the temperatures for the chambers were set to-15℃,-10℃ and-5℃,respectively)and mode 2 (the temperatures for the chambers were set to-20℃,-15℃ and-10℃,respectively).The simulated valueswere in good agreementwith themeasured valueswith themaximumerror of3.1%undermode 1(the simulated mode),and themaximumtemperature uniformity in the chamberswas0.54℃under the two tested modes.The obtained results showed that the temperature distribution within all chambers of this novelmulti-temperature thermostat could keePuniformunder different tested modes.
multi-temperature;thermostat;temperature field;temperature uniformity;FLUENT simulation
TM925.2;TP391.9
A
0253-4339(2015)02-0027-07
10.3969/j.issn.0253-4339.2015.02.027
简介
刘宝林,男,教授,博士,上海理工大学生物系统热科学研究所,13636524955,E-mail:blliuK@163.com。研究方向:低温生物。
2014年7月25日
