基于盲源分离的雷达信号欺骗干扰抑制

李 飞，李国林，粘朋雷

（海军航空工程学院a.研究生管理大队；b.七系，山东烟台264001）

基于盲源分离的雷达信号欺骗干扰抑制

李 飞a，李国林b，粘朋雷a

（海军航空工程学院a.研究生管理大队；b.七系，山东烟台264001）

针对脉冲压缩信号的频谱弥散（SMSP）干扰，通过分析其时频特性，提出了一种基于盲分离的抑制算法。首先，推导了基于独立分量分析的代价函数，由于代价函数中信号概率密度函数不能精确估计，利用信号高阶互累积量的性质，重新构造了一种新的代价函数；其次，利用基于自然梯度的方法对新代价函数进行优化，从而得到基于峭度的盲分离算法；最后，通过仿真证明，对比FastICA算法，文中算法具有更快的收敛速度和更好的分离性能，在保证分离精度的前提下，可成功将目标回波信号分离，达到SMSP干扰抑制的目的。

脉冲压缩；频谱弥散干扰；盲分离；独立分量分析；峭度

被称为“第四维战场”的电子战在现代战争中具有举足轻重的作用，先敌发现，先敌攻击是追求的目标。雷达在电子战中的作用更是无可替代。根据雷达方程，雷达探测距离与距离分辨力是一对矛盾，为解决这一问题，脉冲压缩技术应运而生。脉冲压缩可以使我们获得较长脉冲的平均发射功率，同时得到的距离分辨力对应于一个短脉冲[1]，这使得脉冲压缩技术在多功能和监视雷达中得到广泛应用[2-3]。

伴随着雷达体制的更新干扰技术在不断发展，也衍生出了电子对抗（ECM）与电子反对抗（ECCM）技术。频谱弥散（SMSP）干扰技术是由Sparrow[4]等人发明的，是一种专门针对LFM脉冲压缩体制雷达的新式假目标干扰。SMSP干扰是由多个LFM子脉冲构成，子脉冲个数及调频率取值与接收到的雷达发射的LFM信号有关。雷达接收到夹杂干扰的回波并进行匹配滤波后，SMSP干扰可使匹配滤波的输出具有多瓣结构，从而产生大量的假目标，而且SMSP干扰可先于目标回波发射，一直持续到回波脉宽结束，这样，目标回波的匹配滤波输出将被干扰所覆盖，从而使雷达丢失目标，达到干扰的目的。

孙闽红等[5]提出了基于分数阶傅里叶变换（FrFT）的方法，实现了对SMSP干扰的抑制。尽管FrFT滤波在抗干扰领域中有一定优势，但如果在战场环境中，敌方施加的SMSP干扰具体参数很难捕获，进行FrFT有一定困难。由于盲分离（Blind Source Separation，BSS）方法的特性[6]，分离过程并不需要源信号的先验知识，这在ECCM中具有优势。针对以上情况，本文提出了一种基于盲分离的SMSP干扰抑制算法，通过研究信号高阶累积量的性质，推导出一种新的基于峭度的代价函数，从而避免了对基于Kullback-Leibler散度代价函数中对信号概率密度函数的估计。采用自然梯度方法对新代价函数优化后，最终实现目标回波与SMSP干扰的分离，达到干扰抑制的目的。

1 SMSP干扰模型及BSS模型

1.1 SMSP干扰模型

脉压雷达发射的LFM脉冲可表示为[1]

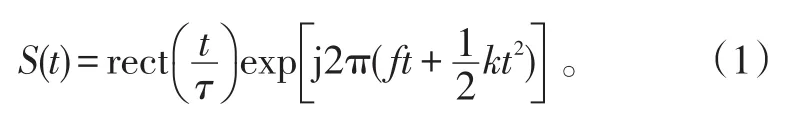
干扰机根据接收到的雷达信号产生的SMSP干扰子脉冲信号模型为

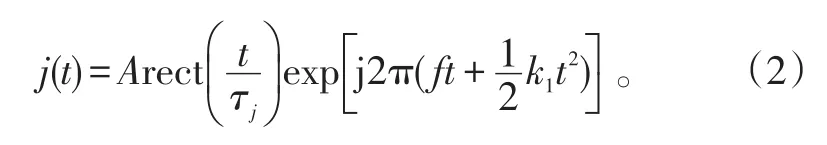
式（2）中：A为干扰信号幅度；τj为干扰信号子脉冲脉宽；k1为干扰脉冲调频斜率。

τj、k1与τ、k的关系：

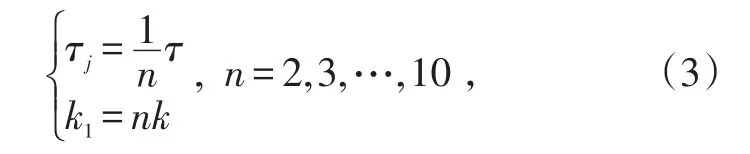
n表示一个SMSP干扰脉冲中含有子脉冲的个数。

将子脉冲重复n次，得到最终SMSP干扰数学模型为[5]：

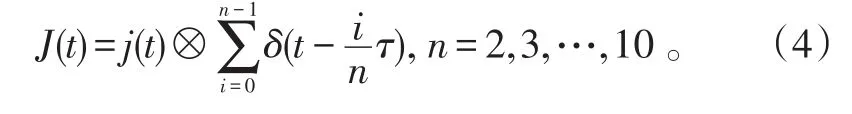
式（4）中：⊗表示卷积算子；i为子脉冲个数；δ(t)为单位采样信号。

1.2 BSS模型

盲信号处理（Blind Signal Processing，BSP）是目前信号处理中最热门的新兴技术之一。盲源分离（Blind Source Separation，BSS）作为盲信号处理领域的一个重要分支，其特点是在传输信道特性和源信号分布未知的情况下，仅从传感器阵列或转换器输出的观测信号中恢复源信号的波形。盲源分离技术已被广泛地应用于雷达、通信、生物医学等学科领域[7]。

典型的盲源分离模型如图1所示[6]：

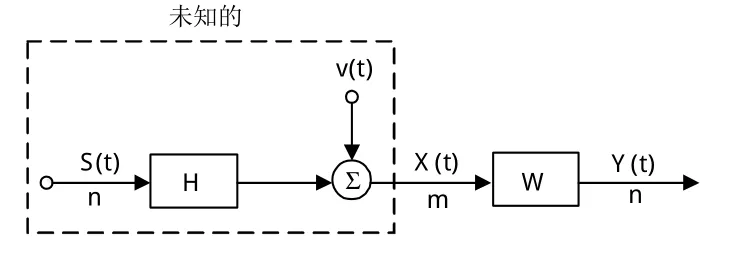
图1 盲源分离问题基本框图Fig.1 Basic block diagram of blind source separation

图1中：S(t)是n维源信号，H是m×n阶混合矩阵，v(t)是加性噪声，在盲分离问题中这些参数认为是未知的。X(t)是m维接收信号；W是n×m阶分离矩阵；Y(t)是分离后的信号。其中：

将式（6）代入式（5）得混合信号的解混系统为

式中，G称为全局矩阵。

在实际情况中，仅由观测信号X(t)完全辨识混合矩阵H是非常困难的[8-9]，根据Cardoso等人提出的矩阵本质相等的理论[10]，BSS问题可重新描述为[6]：只根据传感器输出X(t)辨识混合矩阵H的本质相等矩阵与/或恢复源信号。

本文BSS算法是基于正定盲分离的情况，对于雷达模型，这种假设是成立的。另外，算法是基于高阶累积量，而高阶累积量具有天然抗Gauss噪声的特性，所以在式（7）所描述的信号分离系统模型中，不考虑加性噪声的影响。新的信号分离系统模型为

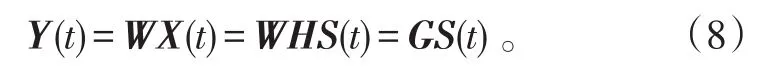
2 SMSP干扰抑制算法

2.1 信号预处理

信号预处理主要白化处理接收信号，其目的是改善算法的收敛特性，并消除冗余或减少噪声。预白化后，BSS任务通常变得容易些，很少出现病态。

首先，估计接收信号协方差矩阵：

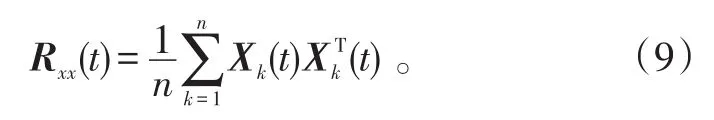
对式（9）进行奇异值分解（SVD）得

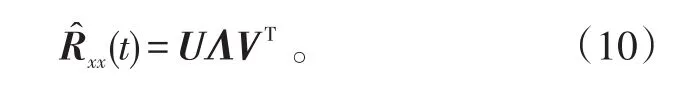
式（10）中：U、V分别为n阶左右奇异值向量矩阵；Λ为n阶对角阵。

预处理后的接收信号为

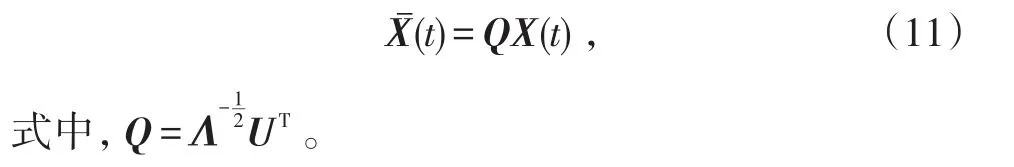
2.2 算法推导

由中心极限定理可知，对比源信号，混合信号更具Gauss性。因此，最大非Gauss性也是BSS问题中信号分离的一个度量。基于这种思想，使用Kullback-Leibler散度作为分离信号独立性的测度，得到自然测度可表示为：

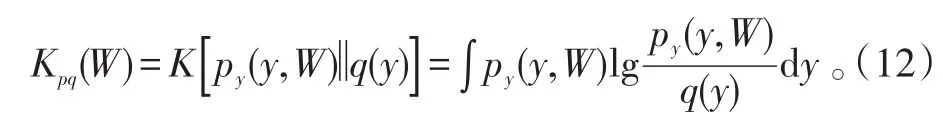
式（12）中：py(y,W)为式（8）所表示系统的概率密度函数；q(y)是分量均统计独立的y的另一个概率密度函数。

当且仅当 py(y,W)与q(y)分布形同时，Kullback-Leibler散度为0。式（12）互信息表示为

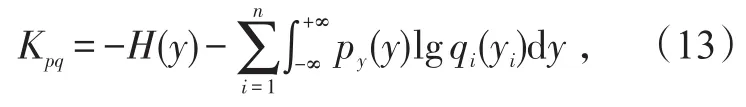
式中，H(y)为分离信号的微分熵。

根据式（8）所表示的分离系统，得到Kullback-Leibler散度代价函数为：

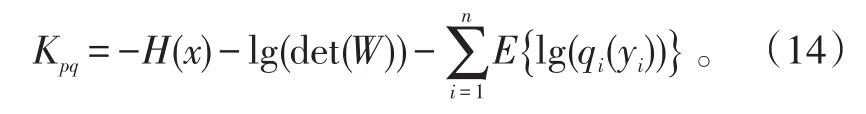
利用自然梯度学习算法使其最小化，得分离矩阵的更新公式为：

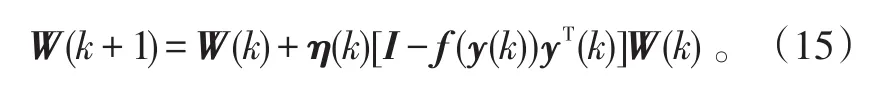
式（15）中：η(k)为学习速率；

f(y)=[f1(y1),f2(y2),…,fn(yn)]T为列矢量，其具体形式为

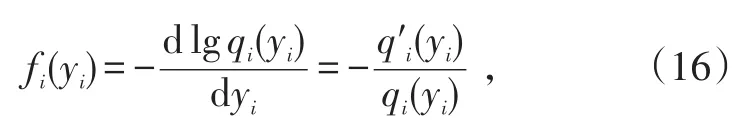
qi(yi)是第i个分离信号的概率密度函数。只要能够知道源信号的概率密度函数，根据式（15）就能求得分离矩阵的最优解。然而，正如前文所言，不可能得知干扰信号的先验知识，若使用非线性函数来估计概率密度函数，或许不可能严格匹配，这可能导致雷达系统丢失目标。基于这种原因，提出另一种基于累积量的代价函数。

对于分离信号，其(p+q)阶互累积量可表示为：

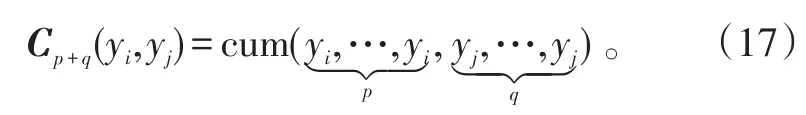
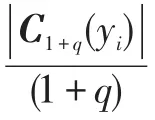
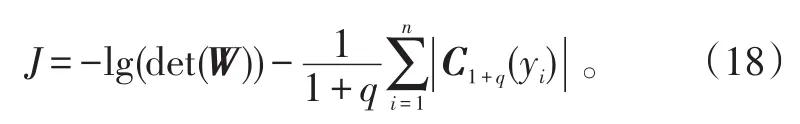
式（18）中，将混合信号微分熵H(x)略去，使它独立于分离矩阵W。利用自然梯度学习算法使其最小化，得分离矩阵的更新公式为：

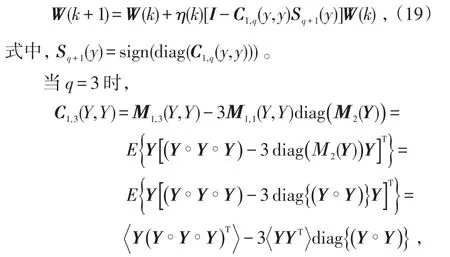
式中，κ表示峭度。

将C1,3(Y,Y)与式（20）代入式（19），得到基于峭度的分离算法为：

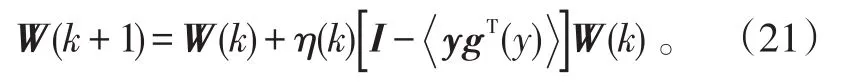
式（21）推导过程中用到了 S4(y)=sign(κ4(y))。g(y)=(y3-3E(y2)y)sign(κ4(y))，为算法激活函数。

对比式（15），新的分离矩阵更新公式只依赖于分离矩阵初值，无需对概率密度函数进行估计，因而提高了算法的可靠性，且更新公式是基于分离信号的四阶累积量。因此，对高斯噪声具有天然的抵抗性。利用式（21）进行迭代，直至算法收敛，得到最终分离矩阵，代入式（8）计算得到最终分离信号。

3 仿真实验及性能分析

图2给出了目标回波信号和SMSP干扰单个脉冲时域波形，其中，SMSP干扰信号脉冲由4个子脉冲组成，即式（4）中n=4，子脉冲调频斜率k1=8×1014，子脉冲脉宽τj=τ/4=0.25 μs，干扰信号幅度是雷达发射信号的10倍。

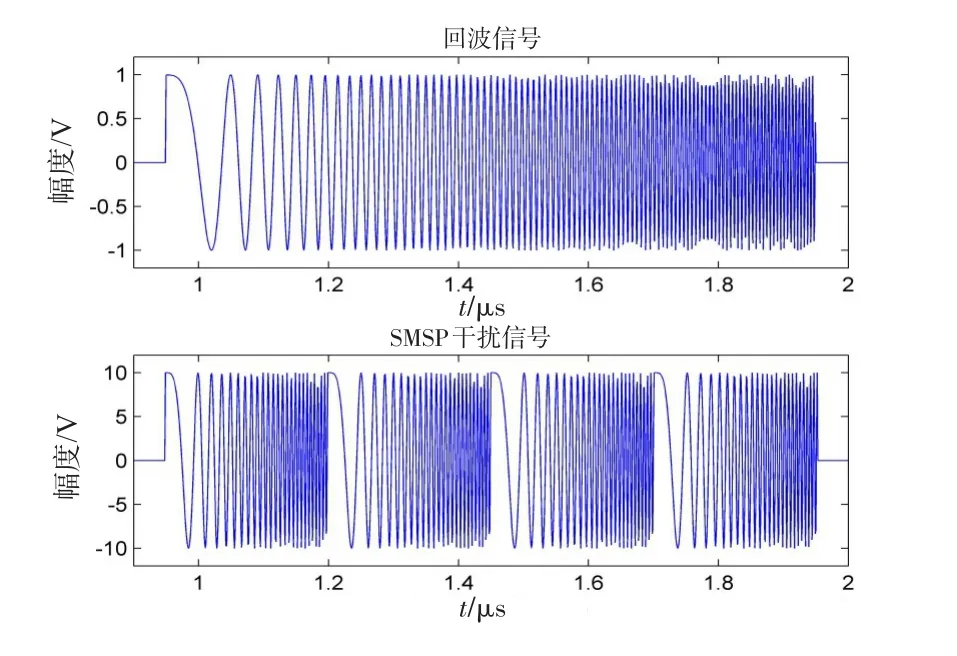
图2 时域波形Fig.2 Waveform of time domain

图3给出了雷达接收到2路被干扰污染的回波时域波形。

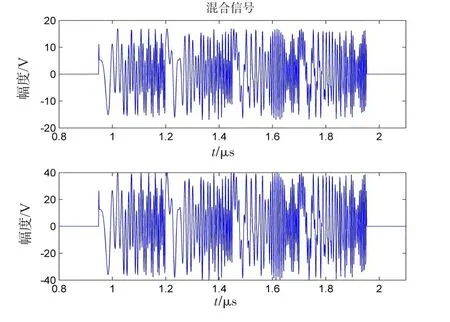
图3 接收信号Fig.3 Receipt signals

从图3中可看到，目标回波已完全被覆盖，时域上回波包含的目标信息已完全丢失，干扰效果非常理想。第2路接收信号频谱如图4所示。对第2路回波信号进行匹配滤波，输出结果如图5所示。LFM信号匹配滤波输出应该是只有1个尖峰，对应目标信息。从图3中看到，对回波进行匹配滤波后，出现无数个尖峰，覆盖区域很宽，雷达观测显示屏上在较大的范围内将对应无数个假目标，哪个是真实目标已无从找起，从而达到了欺骗干扰的效果，对第1路接收信号进行匹配滤波也可得到相似波形，弥散干扰实至名归。

图4 接收信号频谱Fig.3 Frequency spectrum of receipt signal

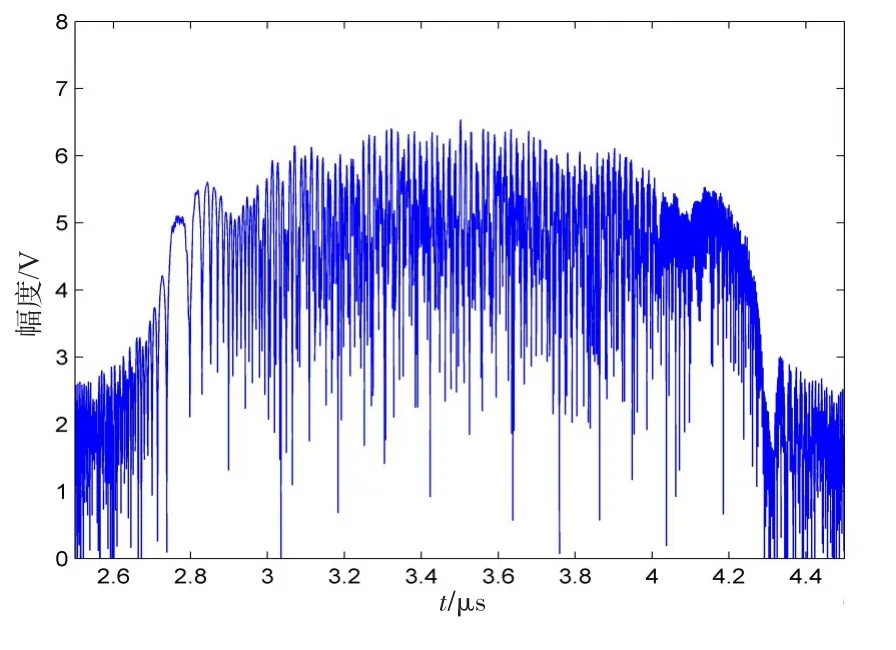
图5 匹配滤波输出Fig.5 Output of matching filter

根据式（21），取η(k)=0.001，分离矩阵W初值随机生成，得出最终混合信号分离效果如图6所示。

图6 分离信号Fig.6 Separate signals

对比图5、7中分离的第1路回波信号经匹配滤波后，尖峰清晰且唯一，说明雷达已经清晰搜索到目标，也证明了分离算法并没有破坏目标回波信号参数形式，分离效果良好，达到SMSP干扰抑制的目的。

图8给出了本文算法相比于著名的FastICA算法的PI值曲线，其定义为[16]：

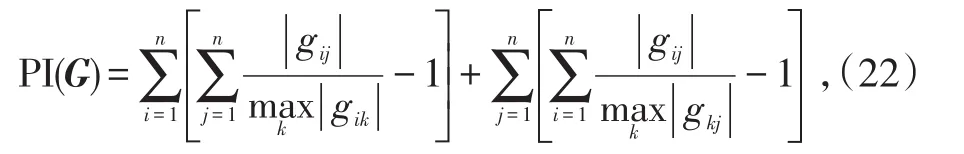
式中，gij是矩阵G中第(i,j)个元素。

PI值越小，说明分离效果越好。

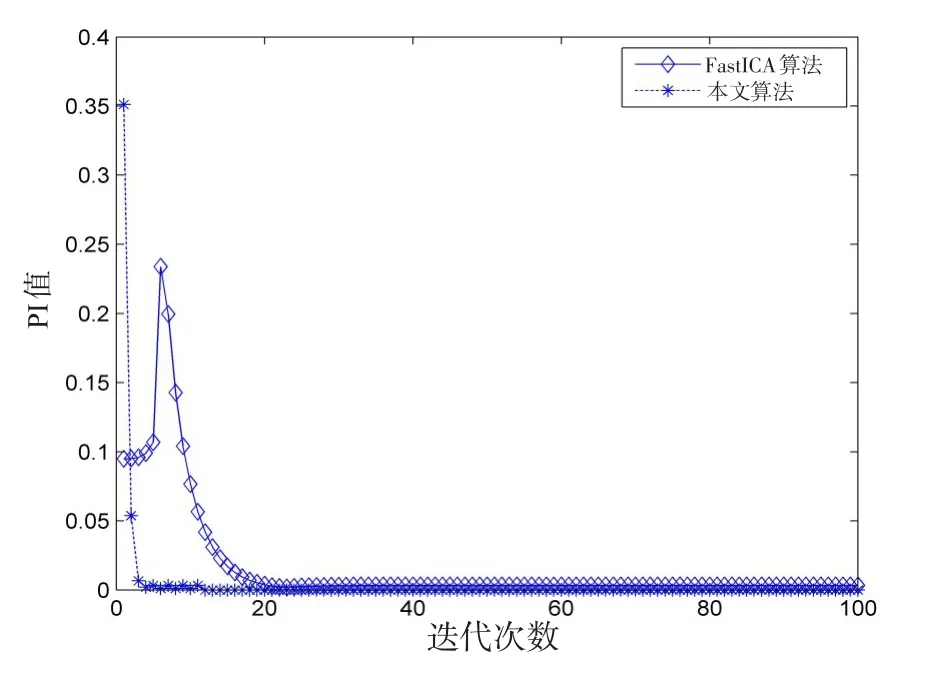
图8 算法PI值曲线Fig.8 PI curve of algorithm

采用FastICA算法也可实现信号分离，但从PI值曲线看出，本算法在迭代至10步时已完全收敛，且稳定性良好，收敛时PI值为0.001 3。而采用FastICA算法时，在迭代至第23步时算法收敛，收敛时PI值为0.003 2，故本节算法优于FastICA算法。

4 结论

本文研究了针对线性调频信号的SMSP干扰，通过分析干扰的时频特性，提出了基于盲分离的干扰抑制方法。推导了基于Kullback-Leibler散度的盲分离代价函数，采用四阶累积量重新构造了基于峭度的代价函数，通过自然梯度的方法对其进行优化，得到分离矩阵迭代公式，将目标回波信号从被干扰污染的混合信号中分离。通过仿真验证了算法相对于FastICA算法具有更好的收敛性和分离性能，达到了SMSP干扰抑制的目的，为ECCM技术提供了一种新方法。

[1]BASSEM R MAHAFZA.雷达系统分析与设计[M].2版.北京：电子工业出版社，2008：4-6. BASSEM R MAHAFZA.Radar systems analysis and design[M].2nded.Beijing：Publishing House of Electronics industry，2008：4-6.（in Chinese）

[2]MARTIN KLEINSTEUBER，HAO SHEN.Blind source separation with compressively sensed linear mixtures[J]. IEEE Signal Processing Letters，2012，19：107-110.

[3]张锡祥，肖开奇，顾杰.新体制雷达对抗导论[M].北京：北京理工大学出版社，2010：59-66. ZHANG XIXIANG，XIAO KAIQI，GU JIE.Introduction to new system radar countermeasures[M].Beijing：Beijing Iinstitute of Technology Press，2010：59-66.（in Chinese）

[4]SPARROW M J，CAKILO J.ECM techniques to counter pulse compression radar：USA.7081846[P].2006-07-25.

[5]SUN MINHONG，TANG BIN.Suppression of smeared spectrum ECM signal[J].Journal of the Chinese Institute of Engineers，2009，32（3）：407-413.

[6]张贤达，保铮.盲信号分离[J].电子学报，2001，29（12）：1766-1771. ZHANG XIANDA，BAO ZHENG.Blind signal separation [J].Acta Electronic Sinica，2001，29（12）：1766-1771.（in Chinese）

[7]DELORME A，SEJNOWSKI T，MAKEIG S.Enhance detection of artifacts in EEG data using high-order statistics and independent component analysis[J].Neuroimage，2007，34（4）：1443-1449.

[8]AISSA EL BEY，LINH TRUNG N，ABED MERAIM K，et al.Underdetermined blind separation of nondiajoint sources in the time-frequency domain[J].IEEE Transaction on Signal Processing，2007，55（3）：897-907.

[9]YIN HONGWEI，LI GUOLIN，LU CUIHUA.Step adaptive normalization blind source separation algorithm[J]. Modern Technologies in Materials，Mechanics and Intelligent Systems，2014，85（2）：1407-1412.

[10]BELOUCHRANI A，ABED MERAIM K，CARDOSO J F，et al.A blind source separation technique using secondorder statistics[J].IEEE Transactions on Signal Processing，1997，45（2）：433-443.

Radar Signal Deception Jamming Suppressing Based on Blind Source Separation

LI Feia,LI Guolinb,NIAN Pengleia
（Naval Aeronautical and Astronautical University a.Graduate Students’Brigade; b.No.7 Department,Yantai Shandong 264001,China）

Through analysis time and frequency domains character of the smeared spectrum（SMSP）jamming which aimed at pulse compression signal,a suppressing algorithm was proposed based on blind source separation.First,the contrast function was deduced based on independent component analysis（ICA）,because the probability density function couldnot be computed accurately,a new contrast function was constructed by using the character high order cumulant.Second,the new contract function was optimized by using natural gradient,and a new blind source separation algorithm was proposed. Last,the experimental simulation proved that the algorithm had faster convergence character and better separation perfor⁃mance than FastICA algorithm,and could separate the target echo from mixed signals with good precision,the purpose to suppress SMSP jamming was achieved.

pulse compression;SMSP jamming;blind source separation;ICA;kurtosis

TN917.3

A

1673-1522（2015）05-0424-05

10.7682/j.issn.1673-1522.2015.05.005

2015-04-21；

2015-06-08

国家自然科学基金资助项目（61102165）

李 飞（1982-），男，博士生；李国林（1955-），男，教授，博士，博导。