Projective Synchronization of One Fractional-order Chaotic System
2015-12-22KONGDefu
KONG De-fu
(College of science,Tianjin University of Technology and Education,Tianjin 300222,China)
0 Introduction
1 System description
Consider the following system:

where x,y,z are the state variables.The chaotic attractors of the system for the order of derivative q=0.98 are displayed through Fig.1 for the parameters,values ɑ=100,b=0.1,c=1.6,d=200.


Fig.1 The phase portrait of the system(1)
2 Projective synchronization
Now,projective synchronization of the fractional -order chaotic system will be studied.For this,the drive system(2)is expressed by

and the corresponding response system(3)is written by

Here u1,u2,u3are the control functions.
Due to facilitate the following analysis,we set the error functions as follows:

Theorem:If control functions are selected as

here k1≤-ɑb,k2≤-d is the real constants.Then,the response system(3)is synchronized with the drive system(2)globally and asymptotically,
Proof:From Eq.(2),(3),(4)and(5),the error systems are achieved as follows:

Let us define a Lyapunov function as follows:
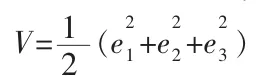
the time derivative of V along the trajectory of the error system(6)leads to
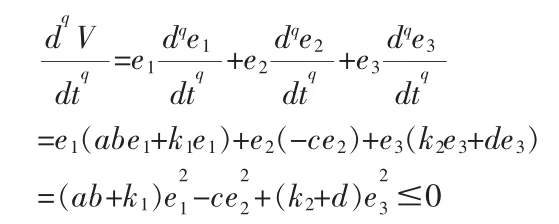
here k1≤-ɑb,k2≤-d is the real constants,since V∈R is positive definite function andis the negative definite function,so according to the Lyapunov stability theory[9],the response system(3)is synchronization to the drive system(2)asymptotically.
3 Numerical simulation
In this section,the constants are taken as k1=-20,k2=-250,α=0.3,and the initial conditions of the drive and response systems are taken as,(x1(0),x2(0),x3(0))=(0.2,0.03,-0.2)and(y1(0),y2(0),y3(0))=(1,0.1,-1).Numerical results is achieved as shown in figure 2.

Fig.2 State trajectories of the errors function of drive system (2) &response system (3)
4 Conclusion
In this letter,projective synchronization of one fractional -order chaotic system is presented,and the chaotic attractor is given.Besides,suitable synchronization controllers are investigated by using the Lyapunov stability theory.Numerical simulations are performed to verify these results.
【Reference】
[1]Yang T,Chua LO.Secure communication via chaotic parameter modulation[J].IEEE Trans Circuits Syst I,1996,43:817-819.
[2]Feki M.An adaptive chaos synchronization scheme applied to secure communication[J].Chaos Soliton Fract,2003,3:959-964.
[3]Li C,Liao X,Wong K.Chaotic lag synchronization of coupled time-delayed systems and its application in secure communication [J].Physica D,2004,194:187-202.
[4]Chang WD.Digital secure comumunication via chaotic systems[J].Digital Signal Process,2009,19:693-699.
[5]Nana B,Woafo P,Domngang S.Chaotic synchronization with experimental application to secure communication [J].Commun Nonlinear Sci Numer Simul,2009,14:2266-2276.
[6]Ott E,Grebogi C,Yorke JA.Controlling chaos [J].Phys.Rev.Lett.,1990,64:1196-1199.
[7]Pecora LM,Carroll TM.Synchronization of chaotic system [J].Phys Rev Lett.,1990,64(8):821-830.
[8]Carroll TL,Pecora LM.Synchronizing a chaotic systems,IEEE Trans Circuits Sys.,1991,38:453-456.
[9]W.Hahn.The Stability of Motion[M].Springer,New York,1967.
