连续箱梁桥车辆荷载效应研究

许 莉，赵素雅，郑圣基

（1.福州大学 土木工程学院，福建 福州350108；2.福州市交通建设集团有限公司，福建 福州350000）

城市桥梁作为城市生命线工程重要的组成部分，是关系到国家经济、民生不可或缺的基础交通设施。随着交通运输事业的飞速发展，桥梁结构的负担日益加重，许多桥梁承载能力逐渐下降，其原因除了长期暴露于自然环境，受到大气中各种腐蚀性气体的侵蚀，再加上施工缺陷、结构本身材料老化、基础变位，以及荷载增加和维修不善等一系列因素的作用外，还与桥梁的车辆荷载设计标准和交通运输车辆状况有很大的关系［1-2］。因此，为了适应我国城市交通运输发展的需要，要求城市桥梁设计规范及标准车辆荷载也要不断更新和提高［3-4］。

本文以连续箱梁桥为研究对象探讨了按照该结构桥梁在新旧规范标准车辆荷载效应作用下各控制截面产生的不同的响应。

1 工程概况

某城市主干道桥梁，该桥设计荷载等级为汽车-超20级，验算荷载挂车-120。主桥上部结构为26.05m+35.00m+26.05m三跨一联预应力现浇混凝土变高连续箱梁，梁高由2.0m渐变至0.9m，横截面为单箱双室，桥梁总宽17.0m，桥梁的立面 图如图1所示。

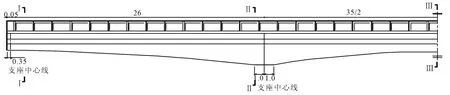
图1 1／2桥立面图（单位：m）

初始设计依据《城市桥梁设计准则》［5］（CJJ1l-93）（简称“93”规范）及《城市桥梁设计荷载标准》［6］（CJJ77-98）（简称“98”规范）均依据《城市桥梁设计荷载标准》［7］（CJJ77-98）（简称“98”规范）和《公路桥涵设计通用规范》［8］（JTJ021-89）（简称“89”规范）规定的材料参数进行取值，而《城市桥梁设计规范》［9］（CJJ11-2011）（简称“11”规范）的取值也与“93”规范规定的一致，因此“93”“98”及“11”规范的材料参数均一致，具体如下：主梁采用50号混凝土，车行道桥面分别采用30号混凝土和沥青混凝土；普通钢筋主筋采用Ⅱ级钢筋，箍筋采用Ⅰ级钢筋，预应力钢筋采用碳素钢丝；二期恒载为55.2kN／m。

2 有限元模型的建立

本文利用空间有限元软件Midas／Civil采用梁单元来模拟并进行有限元的建模［10-11］，模型共有89个单元及98个节点，模型长度单位为m，力的单位为kN，其它单位均由以上单位换算而得，模型截面和单元划分如图2所示。

图2 预应力混凝土连续箱梁桥模型

3 荷载的选取

（1）依据初始设计“93”规范［5］规定采用“89”规范［8］规定的全部荷载选取汽车-超20级为计算荷载，挂车-120为验算荷载。根据规范要求汽车及挂车行驶在行车道上之横向最不利布置如图3和图4所示。

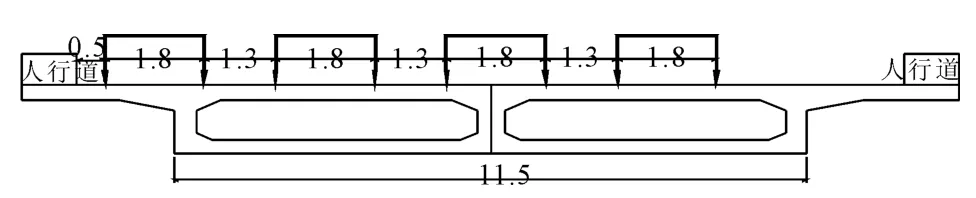
图3 汽车-超20横桥向最不利布置（m）

图4 挂车-120横桥向最不利布置（m）

（2）依据“98”规范［6］规定的基本可变荷载选取城-A、城-B级车道荷载及车辆荷载为标准车辆荷载进行计算。根据规范要求车道荷载、车辆荷载在行车道上之横向最不利布置如图5所示。

图5 城-A级车道及城-A级车辆横桥向最不利布置（m）

（3）依据“11”规范［9］规定的可变荷载选取城-A、城-B级车道荷载及车辆荷载为计算荷载，特种平板挂车-160为验算荷载。根据规范要求车道荷载、车辆荷载及特种平板挂车在行车道上横向最不利布置如图6及图7所示。

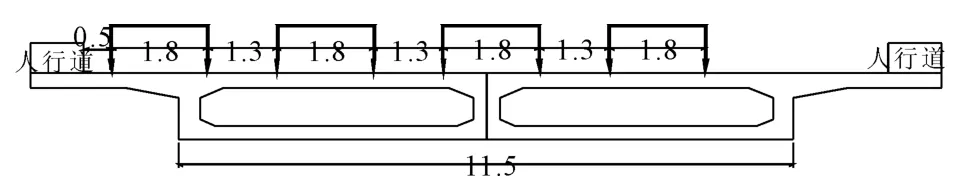
图6 车道及车辆横桥向最不利布置（m）

图7 特种平板挂车-160横桥向最不利布置（m）

4 模型计算结果

本文依据初始设计“93”规范［5］以及“98”“11”规范［6，9］中规定的标准车辆荷载进行选取，并根据规范要求布置在横桥向的最不利位置，计算不同版本规范标准车辆荷载效应及承载能力极限状态下的荷载组合效应。文中取跨中截面和支座截面为控制截面，利用软件分别计算出各控制截面的最大弯矩和最大剪力作为恒载、车辆荷载效应及荷载组合效应值。

4.1 恒载及可变荷载作用计算

不同版本规范规定的恒载及可变荷载作用下利用有限元程序分别计算出主梁边跨跨中和中墩墩顶最大弯矩和剪力值，结果分别见表1和表2。

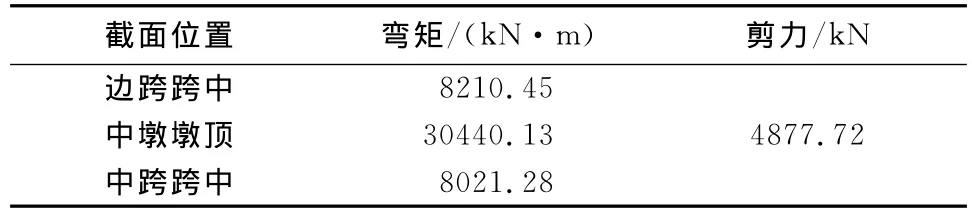
表1 主梁的恒载作用效应

表2 主梁可变荷载作用效应

4.2 主梁恒载及可变荷载组合效应

（1）依据“89”规范［8］第2.1.2条及“85”规范［7］第4.1.2条规定和本文研究目的有选择地进行承载能力极限状态设计时荷载组合（表3），其效应结果值见表4。

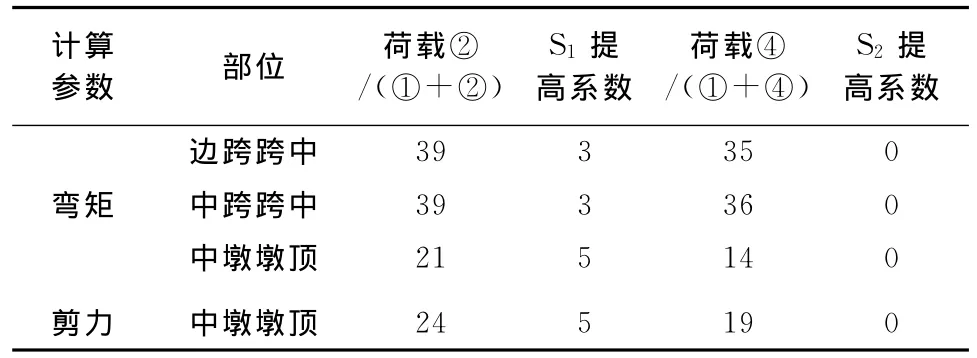
表3 “89”“85”规范承载力极限状态荷载提高系数单位：%

（2）依据“98”规范［6］第3.2.1条及“85”规范［7］第4.1.2条的规定和本文研究目的有选择地进行承载力极限状态设计时荷载组合（表5），其效应结果值见表6。

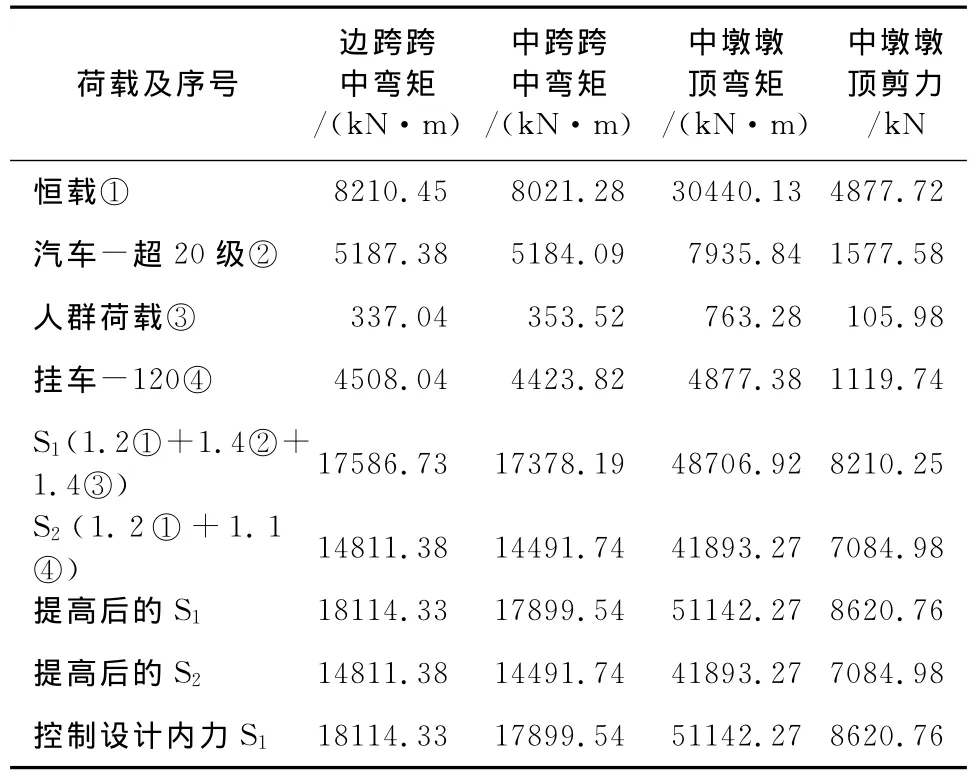
表4 恒载和汽车-超20级、挂车-120荷载效应表

表5 “98”“85”规范承载力极限状态荷载提高系数 单位：%

表6 “98”规范恒载和城-A级、城-B级荷载效应表

（3）依据“11”规范［9］第10.0.1条及“04”规范［12］第4.1.6条的有关规定和本文研究目的有选择地进行承载力极限状态设计时荷载组合（表7），其效应结果值见表8。

表7 “11”“04”规范承载力极限状态荷载提高系数单位：%

5 荷载效应及荷载组合的比较分析

5.1 可变荷载效应的比较

本节根据以上各个规范规定的标准车辆荷载模式、相应荷载等级同时加载在连续箱梁桥上的计算结果，对“98”规范［6］和“11”规范［9］分别与初始设计“93”规范［5］的可变荷载效应进行比较分析。其中图8～图11为“98”规范与“93”规范可变荷载效应比，图12～图15为“11”规范与“93”规范可变荷载效应比。

图8～图11中①代表“93”规范中的汽车-超20级，②代表“98”规范中的城-A级车辆，③代表“98”规范中的城-B级车辆，④代表“98”规范中的城-A级车道，⑤代表“98”规范中的城-B级车道。

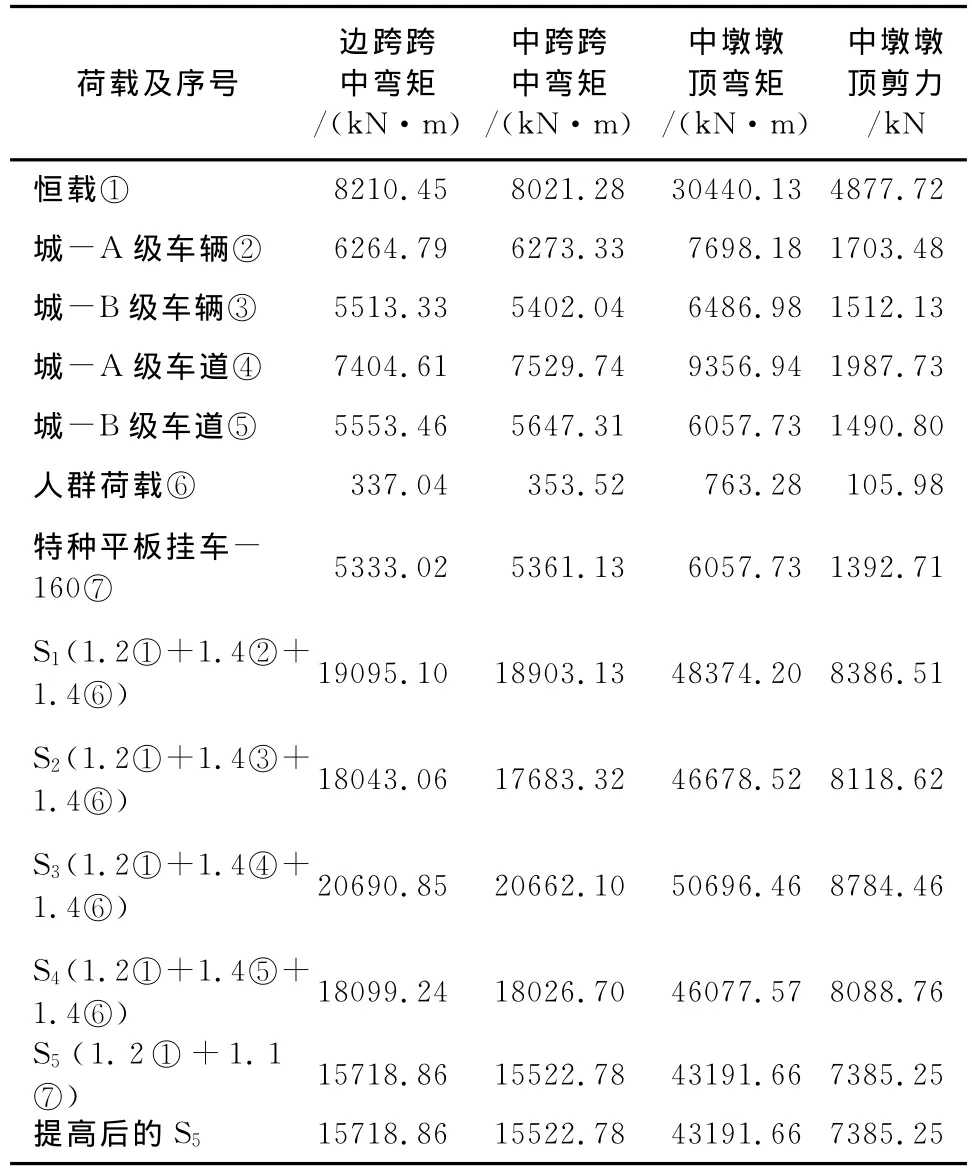
表8 11规范恒载和城-A级、城-B级、特-160荷载效应表

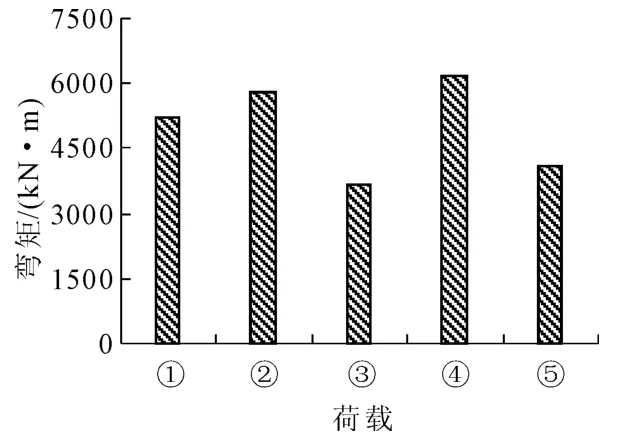
图8 “98”规范与“93”规范边跨跨中弯矩

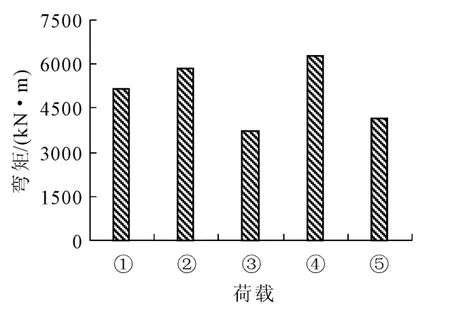
图9 “98”规范与“93”规范中跨跨中弯矩

从图8～图11中可看出，“98”规范的城-A级车辆荷载效应所引起的边跨、中跨跨中和中墩墩顶最大弯矩及中墩墩顶最大剪力与初始设计“93”规范的汽车-超20级车辆荷载产生的结构响应基本相当。不同荷载等级产生的结构响应也有所差异。其中城-A级车辆比汽车-超20级产生的边跨及中跨跨中最大弯矩和中墩墩顶最大弯矩及剪力分别大12.3%、12.5%和小9.8%、大0.4%；城-B级车辆分别小29.0%、28.6%和54.5%、46.5%；城-A级车道分别大19.1%、21.3%和1.3%、13.1%；城-B级车道分别小21.4%、19.5%和23.7%、28.5%。

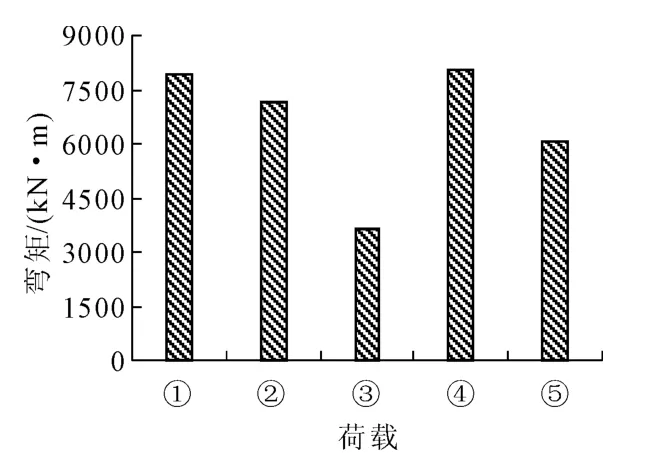
图10 “98”规范与“93”规范中墩墩顶弯矩

图11 “98”规范与“93”规范中墩墩顶剪力

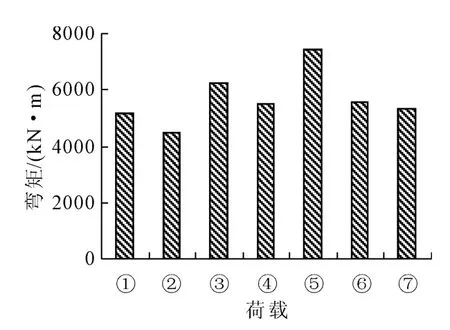
图12 “11”规范与“93”规范边跨跨中弯矩

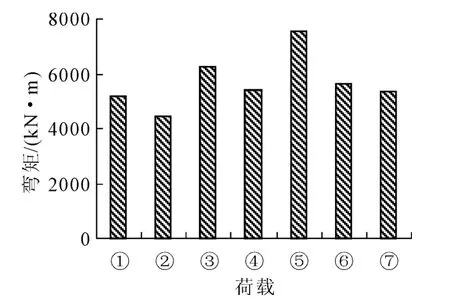
图13 “11”规范与“93”规范中跨跨中弯矩

图12～图15中：①代表“93”规范中的汽车-超20级；②代表“93”规范中的挂车-120；③代表“11”规范中的城-A级车辆；④代表“11”规范中的城-B级车辆；⑤代表“11”规范中的城-A级车道；⑥代表“11”规范中的城-B级车道；⑦代表“11”规范中的特种平板挂车-160。

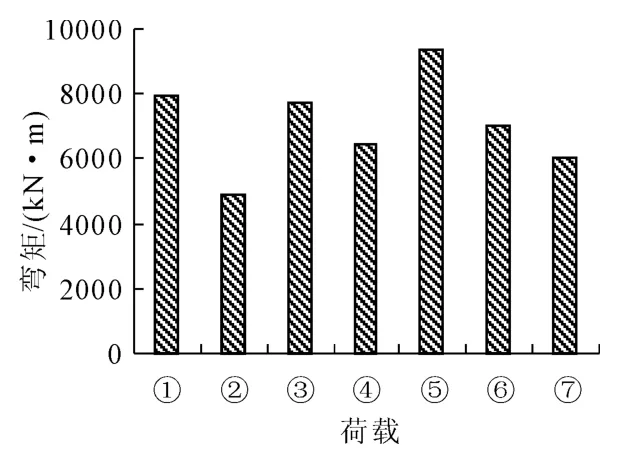
图14 “11”规范与“93”规范中墩墩顶弯矩

图15 “11”规范与“93”规范中墩墩顶剪力

由图12～图15中可得到，“11”规范的城-B级车辆荷载效应所引起的边跨及中跨跨中最大弯矩和城-A级车辆荷载产生的中墩墩顶最大弯矩及剪力与“93”规范的汽车-超20级车辆荷载产生的结构响应基本一致。不同荷载等级产生的结构响应也有所不同。其中城-A级车辆荷载产生的边跨及中跨跨中最大弯矩和中墩墩顶最大弯矩及剪力比汽车-超20级分别大20.8%、21.0%和小3.0%、大8.0%；城-B级车辆分别小6.3%、4.2%和小18.3%及4.1%；城-A级车道分别大42.7%、45.2%和17.9%、26.0%；城-B级车道分别小7.1%、8.9%和11.6%、5.5%；特种平板挂车-160比汽车-超20级分别大18.3%、21.2%和24.2%、24.4%。

5.2 荷载组合效应的比较

本文根据以上各个规范规定的标准车辆荷载模式、相应的荷载等级进行计算的结果，对“98”规范［6］及现行“11”规范［9］分别与初始设计“93”规范［5］在承载能力极限状态设计时荷载组合效应进行比较分析。其中图16～图18为“98”规范与“93”规范荷载组合效应比，图19～图21为“11”规范与“93”规范荷载组合效应比。

从图16～图18中可看出，“98”规范的城-A级车道及车辆荷载在承载能力极限状态下设计时的荷载组合与“93”规范的汽车-超20级车辆荷载组合产生的结构响应基本一致。而不同的等级荷载组合产生的跨中最大弯矩组合及支座最大剪力组合也有所差异。其中城-A级车辆荷载组合产生的边跨及中跨跨中最大弯矩和中墩墩顶最大弯矩及剪力比汽车-超20级分别大5.1%和小2.2%及大0.1%；城-B级车辆荷载分别小10.3%和12.4%、12.5%；城-A级车道荷载分别大7.9%和0.3%、3.5%；城-B级车道荷载分别小8.9%和5.4%、7.7%。

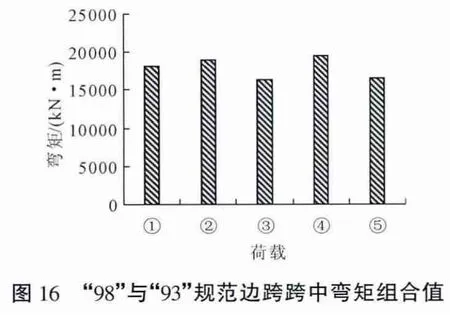
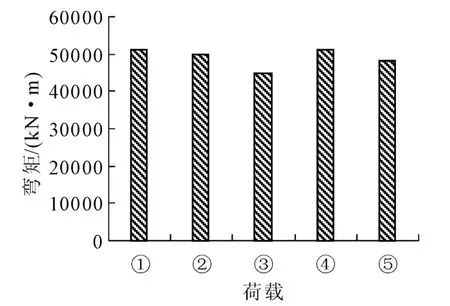
图17 “98”与“93”规范中墩墩顶弯矩组合值

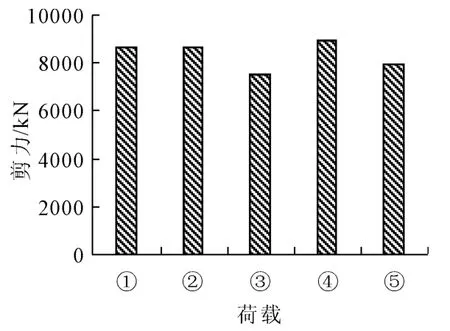
图18 “98”与“93”规范中墩墩顶剪力组合值

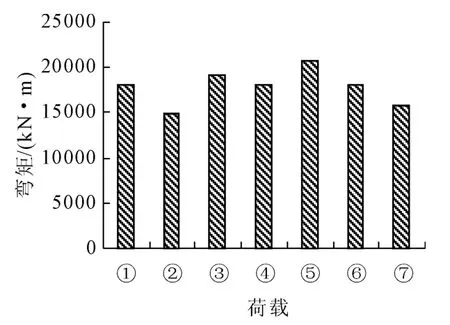
图19 “11”与“93”规范边跨跨中弯矩组合值

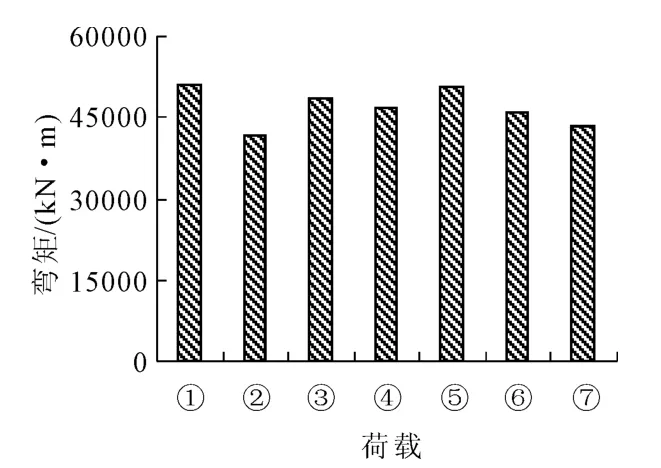
图20 “11”与“93”规范中跨跨中弯矩组合值

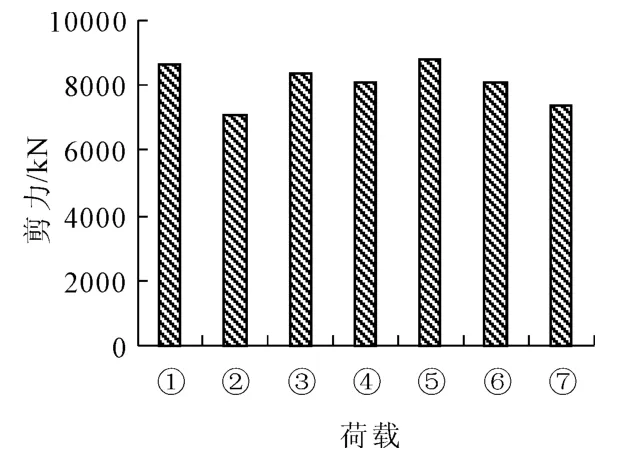
图21 “11”与“93”规范中墩墩顶剪力组合值

由图19～图21中可看出，“11”规范的城-A级车辆荷载在承载能力极限状态下设计时的荷载组合与“93”规范的汽车-超20级车辆荷载组合产生的结构响应基本一致，而特种平板挂车-160与挂车-120也基本相当。不同的等级荷载组合产生的跨中最大弯矩组合及支座最大剪力组合也有所差异。其中城-A级车辆荷载组合产生的边跨跨中最大弯矩和中墩墩顶最大弯矩及剪力比汽车-20级分别大5.4%和小5.4%及2.7%；城-B级车辆分别小0.4%和8.7%、5.8%；城-A级车道分别大14.2%和0.09%、1.9%；城-B级车道分别小0.1%、和9.1%、6.2%；特种平板挂车-160比挂车-120分别大6.1%、3.1%和4.2%。

6 结 论

从以上“98”及“11”规范与初始设计“93”规范在承载能力极限状态设计时荷载组合效应的比较结果，我们可以得到以下结论：

（1）“98”规范规定的城-A级车道及车辆和“11”规范规定的城-A级车辆荷载在承载能力极限状态下设计时的荷载组合与“93”规范的汽车-超20级车辆荷载组合产生的结构响应基本一致，而特种平板挂车-160与挂车-120也基本相当。因此，可近似为同一个等级的荷载组合模式。

（2）“93”规范、“98”规范及现行“11”规范的荷载效应所引起的边跨、中跨跨中最大弯矩和中墩墩顶最大弯矩及剪力与“93”规范的汽车-超20级车辆荷载产生的结构响应基本要大，因此，在进行城市桥梁车辆荷载等级验算时，必须对现有结构型式的桥梁加强各跨跨中抗弯和中墩墩顶处的抗剪验算算。

（3）对于主干路的桥梁来说，该预应力混凝土连续箱梁桥的初始设计汽-超20级荷载等级基本能满足“98”规范的城-A、城-B级车道及车辆荷载和“11”规范的城-A车辆及城-B车道及车辆荷载在承载能力极限状态下设计时的荷载组合所引起的各控制截面的跨中最大弯矩及支座最大剪力的验算要求，而不能满足“11”规范城-A级车道荷载边跨跨中最大弯矩的验算要求，这点也是值得注意。

［1］李文杰.公路桥梁车辆荷载研究［D］.大连：大连理工大学，2009.

［2］Ghosn M，Sivakumar B，Moses F.Modeling maximum live load effects on highway bridge［C］／／Proceedings of the First International Symposium on Life-cycle Civil Engineering.Varenna Lake Como：Tayor ＆Francis，2008：335-341.

［3］Kozikowski M.WIM based live load model foe bridg reliability［D］.Nebraska： University of Lincoln，2009.

［4］Nowak A S.WIM based lived load model for bridges［R］.Florida：Transportation Board，2011.

［5］中华人民共和国建设部.CJJ11-93.城市桥梁设计准则［S］.北京：中国建筑工业出版社，1993.

［6］中华人民共和国建设部.CJJ77-98.城市桥梁设计荷载标准［S］.北京：中国建筑工业出版社，1998.

［7］中华人民共和国交通部.JTJ023-85.公路钢筋混凝土及预应力混凝土桥涵设计规范［S］.北京：人民交通出版社，1985.

［8］中华人民共和国交通部.JTJ021-89.公路桥涵设计通用规范［S］.北京：人民交通出版社，1989.

［9］中华人民共和国建设部.CJJ11-2011.城市桥梁设计规范［S］.北京：中国建筑工业出版社，2011.

［10］邱顺冬，桂满树，姜毅荣.桥梁工程软件 Midas／Civil应用工程实例［M］.北京：人民交通出版社，2011.

［11］邱顺冬，郑海霞，桂满树，等.桥梁工程软件 Midas／Civil常见问题解答［M］.北京：人民交通出版社，2009.

［12］中华人民共和国交通部.JTGD60-2004.公路桥涵设计通用规范［S］.北京：人民交通出版社，2004.