模糊局部均值聚类分割法改进及其应用

刘 璐，吴成茂

（西安邮电大学 电子工程学院，陕西 西安710121）

0 引 言

由于图像来源千差万别，导致图像像素分布具有多样性，直接采用传统模糊C－均值聚类算法很可能无法获得其满意的分割效果，其主要原因在于它利用像素灰度信息且未考虑像素与其周围邻域像素之间的关联性［1－4］。为此，学者们提出具有一定抗噪性的二维或三维直方图模糊C－均值聚类分割算法［5－7］，以及融入像素空间邻域信息的改进模糊C－均值聚类分割方法［8－11］，但是，它不适合复杂图像中目标和背景所占图像比例相差悬殊的情形。为了进一步增强具有空间信息约束的模糊C－均值聚类分割算法的鲁棒性和抗噪性，Krinidis等［12］提出了一种基于模糊局部信息C－均值聚类算法，其充分利用像素与其邻域像素之间的空间信息和灰度信息，得到一种具有较强普适性的图像分割算法，其分割性能优于现有众多结合空间信息的模糊C－均值聚类分割算法，但是相比吴一全等［13］提出的新空间信息模糊C－均值聚类算法性能差。为了增强文献 ［12］模糊局部信息C－均值聚类算法的抗噪性能和分割性能，公茂果等［14］提出了改进再生核空间的模糊局部信息C－均值聚类分割算法，其抗噪能力得到极大改善，并在医学图像［15］和遥感图像［16］分割中得到了成功应用。通过对文献 ［12，14］进行认真分析，发现模糊局部C－均值聚类算法的聚类中心迭代公式存在一定的理论缺陷，于是利用拉格朗日乘数法对模糊局部信息C－均值聚类目标函数求偏导并严格推导得到正确的隶属度和聚类中心迭代表达式。实际图例分割测试和比较结果表明修改后的表达式是正确的，同时对遥感图像的分割验证了本文获得的模糊局部C－均值聚类算法具有一定潜在优势。

1 模糊C－均值聚类

传统模糊C－均值模糊聚类是一种非监督聚类方法，已广泛应用模式识别与图像处理等众多领域。模糊C－均值聚类所对应的目标函数可表示为

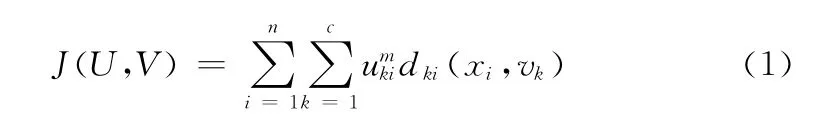
式 中：c——聚 类 的 类 别 数，vk——区 域 的 聚 类 中 心，uki——x 属于k 类区域的隶属度。dki＝xi－vk2是内积矩阵范数，表示样本点x 距聚类中心vk的欧氏距离。一般选取参数m 为1.5、2.0和2.5，常取2.0。隶属度uki应满足如下条件：

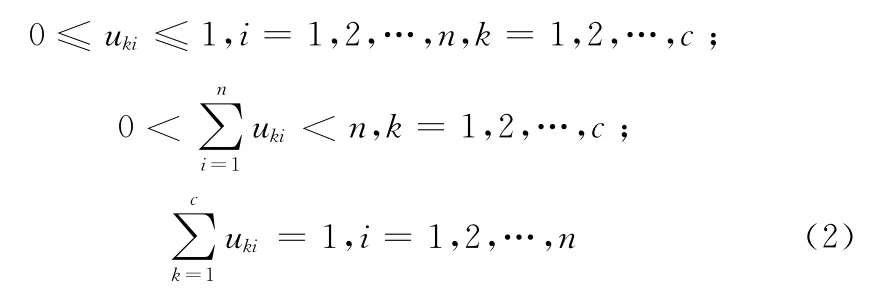
其隶属度和聚类中心表达式为

利用式 （3）和式 （4）可实现模糊C－均值聚类。若算法终止并遵循最大隶属度原则实现样本归类。

2 模糊局部C－均值聚类分割法

为了改善传统模糊C－均值聚类分割图像未考虑像素邻域信息的不足，希腊学者Krinidis等［12］提出了一种新的具有鲁棒性模糊局部信息C－均值聚类算法，充分利用像素与其邻域像素之间的空间信息和灰度信息，无需人工参数选取，极大地增强了算法的实用性。

2.1 模糊局部C－均值聚类分割法算法

模糊局部信息C－均值聚类目标函数中含有模糊因子Gki，而权因子充分考虑像素与其邻域像素之间空间信息和灰度信息，提高了对噪声图像分割的鲁棒性。其聚类分割目标函数表达式如下

其中

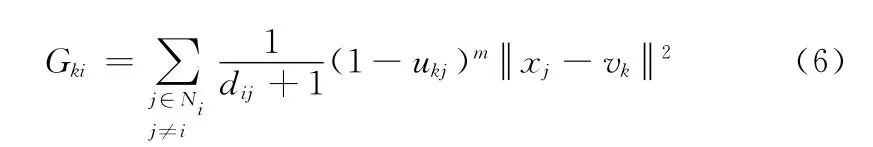
式中：xi——中心像素，xj——邻域像素， xj－xi2——邻域像素到中心像素的欧氏距离，uki——像素xi属于第k类区域的隶属度，vk——第k 类的聚类中心，m 是模糊性加权指数。在满足隶属度uki之和为1的条件下，根据拉格朗日乘子法求目标函数Jm的极小值，文献 ［12］给出的聚类中心和隶属度矩阵结果

2.2 模糊局部C－均值聚类分割法问题分析与改正

通过对文献 ［10］模糊局部C－均值聚类演算法分析发现，其隶属度迭代式 （7）是按照如下目标函数

其中

利用拉格朗日乘子法求其偏导并且令偏导为零得到的。但是其聚类中心迭代表达式 （8）并不是根据目标函数 （9）运用拉格朗日乘子法求其偏导并且令偏导为零得到的，它是由传统模糊C－均值聚类目标函数式 （1）运用拉格朗日乘子法求其偏导并且令偏导为零得到的，而理论上，模糊局部C－均值聚类算法的目标函数式 （9）是在传统模糊C－均值聚类算法中的目标函数式 （1）的基础上进行改进的，所以两个迭代表达式相差甚大。这就导致了希腊学者所提出的聚类中心迭代式 （8）与其正确的目标函数式 （9）严重的不一致，下面将对其进行分析推导及改正。

利用拉格朗日乘子法建立新的无约束优化的目标函数为

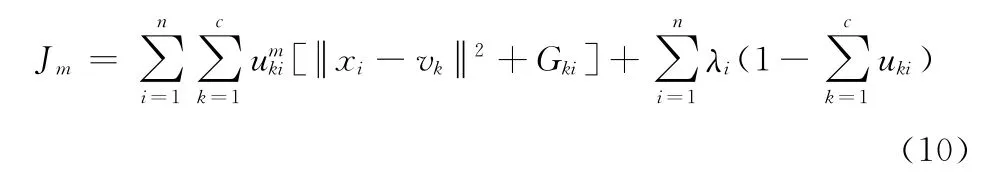
对目标函数关于隶属度uki求导并令其导数为零，即

化简得

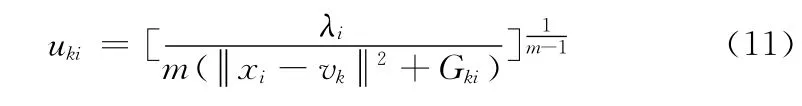
将式 （12）代入式 （11）解得

对目标函数关于聚类中心vk求导并令其为零，即

其中

解得

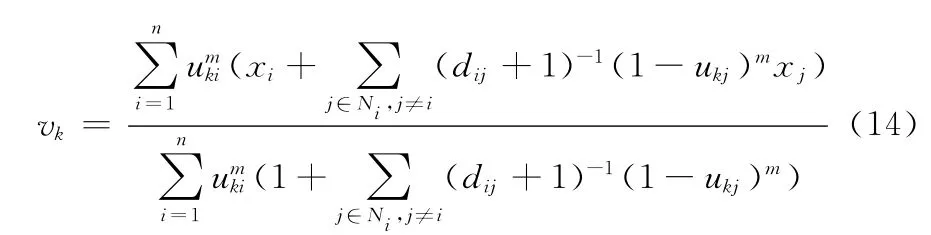
上述推导所得隶属度迭代表达式 （13）与希腊学者的隶属度迭代表达式 （7）一致，但是正确的聚类中心迭代式（14）与希腊学者的聚类中心迭代式 （8）有很大的差异，可以看出希腊学者没有考虑到像素点x 的邻域像素点xj对聚类中心的影响。从而进一步说明了聚类中心迭代式 （8）是不科学的。

3 核空间模糊局部C－均值聚类分割法

为了改善模糊局部信息C－均值聚类分割算法的分割精度和抗噪能力，我国学者公茂果等［14］提出了改进型核函数模糊局部C－均值聚类分割法。

3.1 核函数的引入

近年来，利用核函数将非线性规划问题转化成线性问题来求解是机器学习中的一个热点，核函数的主要思想是：构造新的特征向量，将输入低维空间映像到高维特征空间，从而使原输入空间的非线性问题转化为高维空间的线性问题。其定义如下

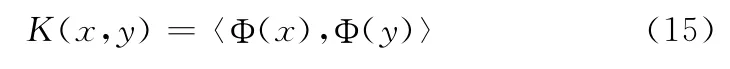
式中：x——输入空间，Ф（x）——特征空间，Ф：x→Ф（x）是核函数导出的特征变换，一般情况下，变换函数Ф（x）要比核函数K（x，y）复杂的多。目前来说有很多种内核函数，不同的内核函数对于原始空间会产生不同的测度。高斯核函数是最广泛应用之一。表达式为

式中：σ——尺度参数，σ表达式为

式中：di＝ xi－是像素xi到聚类中心的距离，是di的均值，聚类中心的值和di的均值d珚 的表达式分别为

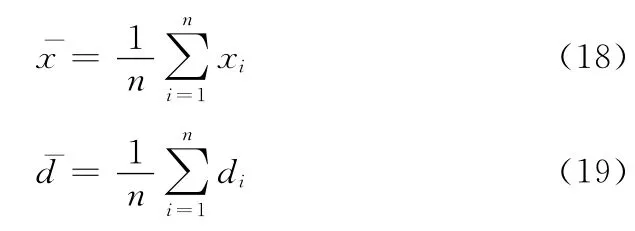
3.2 核函数模糊局部C－均值聚类分割法

为了进一步增强图像分割的抗噪能力，公茂果等［14］通过引入内核函数对模糊局部信息C－均值聚类算法进行改进，即核函数模糊局部C－均值聚类算法。基于核函数的聚类算法有很多优点：①对图像的特征具有很好的适应性；②不需要先验知识来确定各区域的拓扑结构；③对噪声具有很好的抑制能力。文献 ［14］所给的目标函数如下所示

式中：G′ki——新的模糊因子。模糊因子的公式

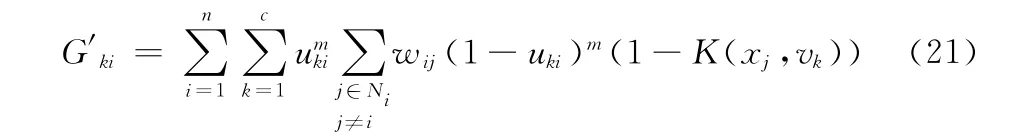
式中：uki——第x 个像素属于第k 类区域的隶属度，K（xi，vk）——核函数，wij——权模糊因子。文献 ［14］给出的求目标函数Jm的极小值并所使用的隶属度和聚类中心迭代表达式分别如下

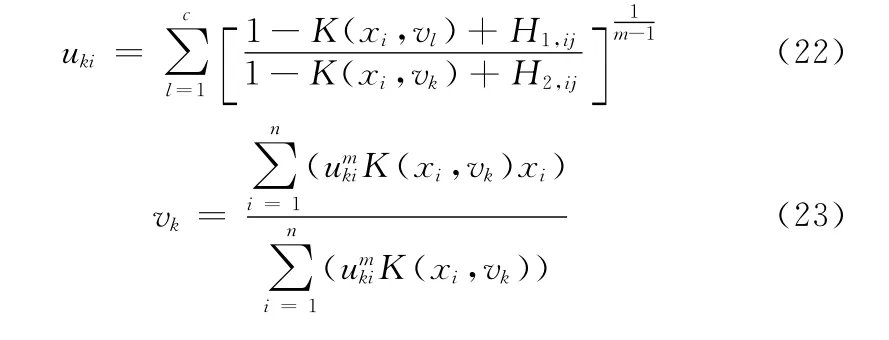
其中

3.3 核函数模糊局部C－均值聚类分割法的分析与改正

对公茂果等的核函数模糊局部C－均值聚类所对应的聚类中心迭代式 （23）分析发现，它与模糊局部C－均值聚类算法中所求的聚类中心迭代式 （8）存在类似的错误，下面将对其进行分析推导及改正。

根据拉格朗日乘子法建立新的无约束优化聚类目标函数为

对目标函数关于隶属度uki求导并令其导数为零，即

化简得

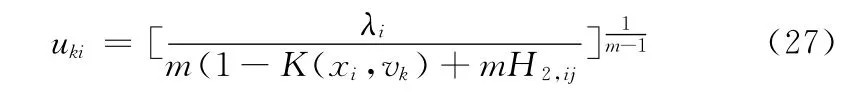
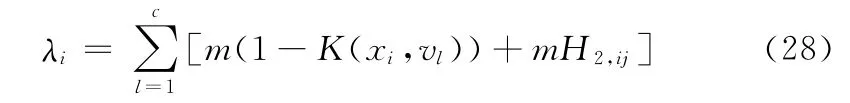
将式 （28）代入式 （27）解得

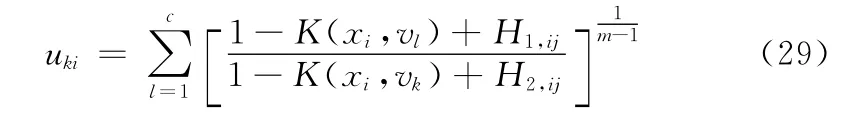
对目标函数关于聚类中心vk求导并令其为零，即

解得

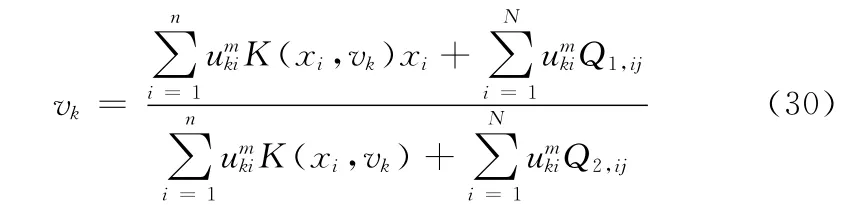
其中，Q1，ij和Q2，ij分别表示为

上述表达式 （30）与文献 ［14］聚类中心表达式 （23）存在巨大差异，其中聚类中心表达式 （23）是核空间模糊C－均值聚类算法的聚类中心表达式，它与核空间模糊C－均值聚类分割算法的目标函数不吻合。针对本文所获得的核空间模糊局部C－均值聚类所对应的隶属度和聚类中心表达式 （29）和式 （30），本文根据分析与推导设计一种核函数模糊局部C－均值聚类分割算法如下：

步骤1 确定聚类数目c（2≤c≤n），窗口大小Ni，模糊指数m，设定终止迭代条件阈值ε。

步骤2 随机初始化聚类中心。

步骤3 设定循环次数计数器r＝0。

步骤4 利用文献 ［13］中相邻像素权系数计算表达式计算权重因子wij值。

步骤5 利用式 （29）更新模糊隶属度矩阵。

步骤6 利用式 （30）更新聚类中心。

4 实验结果与分析

为了验证本文所提出的图像分割算法的有效性，本文在实验运行环境为Matlab7.0，算法参数选取模糊因子m＝2，迭代误差ε＝0.01，最大迭代次数Tm＝500的条件下，对人工合成图像 （如图1 所示）和复杂遥感图像 （如图2所示）分别添加概率为0.1，0.3的随机椒盐噪声，以及均值为0且均方差分别为57 和80 的高斯噪声，采用文献［14］所建议的分割算法和本文所提出的分割算法对其进行分割测试。

图1 （a）为人工合成图像，图1 （b）为其添加概率为0.3椒盐噪声干扰图像，图1 （c）为采用文献 ［14］聚类算法分割结果，图1 （d）为采用本文算法分割结果。由两种聚类分割结果来看，两种分割结果相近，将子图1 （c）和子图1 （d）相比较，其分割效果非常相似，差异很小，由此表明对于人工合成简单对称图像采用文献 ［14］所建议的算法和采用本文所提出的算法分割效果相当，表明本文所建议的分割算法是正确的。

图1 30%椒盐干扰图像及其分割结果

图2 （a）为遥感图像，图2 （b）为其添加概率为0.1的椒盐噪声干扰图，图2 （c）为采用文献聚类算法分割结果，图2 （d）为采用本文算法分割结果。由分割结果来看，两种聚类分割结果明显不同，通过对比子图2 （c）和子图2（d）的标识区域发现，子图2 （d）所标注的长方形和椭圆区域显然要比子图2 （c）所标注的长方形和椭圆区域分割效果好，子图2 （c）中对于颜色较深的地方并没有有效的分割出来，子图2 （c）所标注的正方形区域要相比较于子图2 （d）所标注的正方形区域较好。总体来说采用本文聚类算法的抗噪性能比文献［14］聚类算法更有一定的优势。

图3 （a）为筛子图像，图3 （b）为其添加均值为0且均方差为80 的高斯噪声干扰图像，图3 （c）为采用文献［14］聚类算法分割结果，图3 （d）采用本文聚类算法分割结果。由两种聚类分割算法所得结果来看，二者分割结果存在显著差别，其中子图3 （d）所标注的椭圆区域比子图3 （c）所标注的椭圆区域分割的效果好，使得图像轮廓更加完整。说明采用本文聚类算法的分割效果明显优于采用文献 ［14］的聚类方法分割效果。

图2 10%椒盐干扰图像及其分割结果

图3 10%高斯干扰图像及其分割结果

图4 （a）为遥感图像，图4 （b）是添加均值为0且均方差为57 的高斯噪声干扰图像，图4 （c）为采用文献［14］聚类算法分割结果，图4 （d）为采用本文聚类算法分割结果。由两种算法分割结果来看，二者分割结果存在一定的差异，其中子图4 （d）所标注的长方形区域比子图4（c）所标注的长方形区域分割效果好，子图4 （c）所标注的长方形区域出现明显的断裂，不能保证分割图像的完整性。另外，子图4 （d）所标注的小正方形区域和大正方形区域比图4 （c）所标注的小正方形区域和大正方形区域更加平滑连续。

综合上述不同强度的椒盐与高斯噪声干扰遥感图像的分割结果来看，本文所建议的核空间模糊局部信息C－均值聚类算法相比文献 ［14］算法更适合强噪声干扰图像分割需要，并且表现出良好的抗噪性能。

图4 5%高斯干扰图像及其分割结果

5 结束语

本文针对模糊局部聚类算法的聚类中心迭代表达式与其聚类目标函数不一致的缺陷，对聚类目标函数采用拉格朗日乘子法重新推导并设计一种核空间模糊局部C－均值聚类分割算法，改善了模糊局部信息C－均值聚类算法的致命缺点即无法收敛至局部极小值点，使算法具有收敛性。相比文献 ［14］中的算法，本文所提出的改进的模糊局部均值聚类分割法不仅提高了复杂遥感等图像强噪声干扰分割的抗噪能力，而且对于探讨新的模糊鲁棒分割算法具有积极的促进作用。

［1］Li G，Liao T，Hu J.Application of fuzzy cluster analysis on identifying sedimentary microfacies［J］.IEEE Trans on Computational and Information Sciences，2013，5 （9）：1235－1237.

［2］Uesu H，Nagashima K，Hsunhsun Chung，et al.Relational structure analysis of fuzzy graph and its application：For analyzing fuzzy data of human relation ［J］.IEEE Trans on Image Processing，2013，22 （2）：573.

［3］Thakurl E P，Madaan E N.A survey of image segmentation techniques［J］.International Journal of Research in Computer Application and Robotics，2014，2 （4）：158－165.

［4］Li C，Huang R，Ding Z，et al.Level set method for image segmentation in the presence of intensity in homogeneities with application to MRI［J］.IEEE Trans Image Process，2011，20（7）：2007－2016.

［5］CHEN Ziyang， WANG Baoping.An image segmentation method based on 3－D histogram and RFKCN ［J］.Chinese Journal of Computers，2011，34 （8）：1156－1162 （in Chinese）.［陈子阳，王保平.一种基于三维直方图和RFKCN 的图像分割方法［J］.计算机学报，2011，34 （8）：1156－1162.］

［6］Zhou Xiancheng，Shen Quntai，Liu Limei.New two－dimensional fuzzy C－means clustering algorithm for image segmentation ［J］.Journal of Central South University of Technology，2008，15：882－887.

［7］SUN Wenbang，TANG Haiyan，CHEN Hexin，et al.Based on the three dimensional histogram clustering features of unsupervised image change detection method ［J］.Journal of Shanghai Jiaotong University，2012，46 （2）：245－245 （in Chinese）.［孙文邦，唐海燕，陈贺新，等.基于三维直方图聚类特性的非监督图像变化检测方法 ［J］.上海交通大学学报，2012，46 （2）：245－249.］

［8］Zhong Y F，Ma A L，Zhang L P，et al.An adaptive memetic fuzzy clustering algorithm with spatial information for remote sensing imagery ［J］.IEEE Journal of Selected Topics in Applied Earth Observations and Remote Sensing，2014，7 （4）：1235－1248.

［9］Gong M G，Su L Z，Jia M，et al.Fuzzy clustering with a modified MRF energy function for change detection in synthetic aperture radar images ［J］.IEEE Trans on Fuzzy Systems，2014，22 （1）：98－109.

［10］Devi P R，Mohan N，Kumar V P，et al.C－Means with fuzzy local information ［J］.Data Mining and Knowledge Engineering，2011，3 （16）：952－960.

［11］Li Y，Shen Y.Fuzzy c－means clustering based on spatial neighborhood information for image segmentation ［J］.Journal of Systems Engineering and Electronics，2010，21 （2）：323－328.

［12］Krinidis S，Chatzis V.A robust fuzzy local information Cmeans clustering algorithm ［J］.IEEE Trans on Image Processing，2010，19 （5）：1328－1337.

［13］WU Yiquan，SHEN Yi，TAO Feixiang.An algorithm of remote sensing image clustering based on kernel fuzzy c means with local spatial information ［J］.Journal of Geo－information Scienece，2014，16 （5）：769－775 （in Chinese）. ［吴一全，沈毅，陶飞翔.基于局部空间信息KFCM 的遥感图像聚类算法 ［J］.地球科学信息学报，2014，16 （5）：769－775.］

［14］Gong M G，Liang Y，Shi J，et al.Fuzzy c－means clustering with local information and kernel metric for image segmentation ［J］.IEEE Trans on Image Processing，2013，22 （2）：573－584.

［15］LIN Liqiu，CHEN Liangliang.The medical image segmentation research ［J］.Journal of Information Science and Technology，2011 （21）：412－412 （in Chinese）. ［林丽秋，陈亮亮.医学图像分割研究概况 ［J］.科技信息，2011 （21）：412－412.］

［16］Xiang D L，Tang T，Hu C B，et al.A kernel clustering algorithm with fuzzy factor：Application to SAR image segmentation ［J］.IEEE Geoscience and Remote Sensing Letters，2014，11 （7）：1290－1294.