基于密集点云重投影的三维线段模型重建算法

欧元汉，黄 鸿＋，陆宇海

（1.广西大学 计算机与电子信息学院，广西 南宁530004；2.南宁有无科技有限公司，广西 南宁530007）

0 引 言

基于图像的三维重建过程主要包括密集点云生成、曲面重建、纹理映射等步骤。密集点云模型在缺乏纹理的地方出现空洞，在建筑物边缘容易产生重建误差较大的外点。以上缺陷导致由密集点云生成的网格模型表面出现起伏凹陷，本该平直而锐利的边缘出现扭曲和平滑。直线是建筑物表面和边缘最常见的几何元素，相比密集点云模型，建筑物的三维线段模型能有效体现建筑物的几何结构并保留规整的建筑物边缘。生成网格模型时，借助三维线段模型提供的边缘信息，可使网格模型具有更加平整的表面和锐利的边缘，改善后续产生的贴图模型的视觉效果。因此建筑物场景的三维线段模型有重要的实用价值。

1 相关工作

三维线段模型重建的主要过程包括多视图间线段匹配和三维线段生成。

多视图间线段匹配问题的本质是寻找同一三维线段在各视图中的重投影线段。线段匹配的难点在于受光线，角度和遮蔽等因素影响，各视图中的线段端点不一致；在不同拍摄角度下，建筑物边缘线段周围的背景有较大反差，基于线段附近区域灰度值的匹配方法很难奏效。Bay等［1］提出使用直线表面特征和拓扑关系匹配线段，用线段附近的颜色直方图进行初匹配，根据线段间的拓扑关系去除误匹配，寻找新匹配。该方法计算量大，且颜色特征对光照和图像间反差敏感；Wang等［2］利用线段周围像素的梯度信息构建MSLD 线段描述子用于线段匹配，但线段周围往往缺乏丰富的纹理，且该方法不能处理尺度变换问题；Wang等［3］使用线段端点计算线段间的角度和长度比例，根据这些信息进行线段匹配，该方法在端点位置出现较大误差时无法奏效；Fan等［4］先对图像进行特征点匹配线段，然后基于线点不变性 （line－point invariants）匹配线段，该方法能稳健处理旋转、尺度和光照变换问题，匹配准确率高，但受制于稀疏的特征点匹配，匹配线段数量不够多。

得到多视图间线段的匹配关系后，可用平面交线法［5］重建三维线段，该方法受线段端点位置不准确的影响，对输入图像的几何约束太强，不能有效处理误匹配线段，导致三维线段出现较大的估计误差，模型中充满杂线；Chen等［6］提出的建筑物三维线段模型的方法，该方法重建速度快，但依靠点云模型确定线段端点，使得线段模型过度依赖于点云模型。当点云模型出现局部稀疏或缺失时，会影响线段模型的完整重建；点云在建筑物边缘并非整齐分布，造成线段模型在边缘处出现不规整的线段。Hofer等［7，8］通过对极几何产生潜在匹配线段，生成大量候选三维线段，最后通过三维线段聚类滤除多余杂线，形成最后的三维线段模型。该方法主要用于重建输电塔这类纹理很少的直线框架物体，所以不要求准确匹配线段，但需生成数量庞大的候选三维线段，计算量大，重建速度慢，不适用于实体建筑物重建。

为解决上述问题，本文提出了基于密集点云重投影的三维线段重建算法。主要贡献有：①使用关联同一空间点的二维线段存在匹配关系原理构建匹配线段集，避免依赖线段纹理特征，解决点云重投影后产生的深度信息丢失问题，实现多视图间线段的准确匹配；②针对以往方法对噪声敏感的问题，本文采用空间直线与空间平面相交法重建三维线段，并以RANSAC［9］滤除因线段误匹配产生的杂线，实现三维线段的稳健估计；③定义三维线段的重投影误差，并以最小化重投影误差方法优化三维线段模型，使模型精度进一步提高。

2 算 法

本文提出的建筑物三维线段模型重建算法的主要流程是：①由SFM 和MVS算法生成密集点云和各视图的摄相机矩阵；②在各视图中的提取二维线段；③将密集点云重投影回各视图中获得线段的匹配关系；④使用空间直线与空间平面相交法重建三维线段；⑤最小化三维线段的重投影误差，优化场景模型。

2.1 线段检测

LSD （line segment detector）［10］线段提取算法对具有同一梯度方向的像素集合应用最小二乘法估计线段的方向和端点，检测精度高和误检率低，计算复杂度正比于图像像素总数，检测速度快，适合大规模图像的二维线段提取。

LSD 算法输出线段的两个端点坐标和外接矩形。在线段外接矩形内的所有像素构成称为线段支持区域 （line support region）的像素集合。各线段的支持区域之间没有交集，所以三维空间中的一点X 重投影回某一视图后只有两种可能：若重投影点x 在某一线段l 的支持区域内 （x∈l）则此三维点X 关联该线段，若重投影点不在任何线段的支持区域内则三维点X 不关联任何线段。

2.2 线段匹配

2.2.1 线段的弱匹配

本文使用关联同一空间点的线段存在弱匹配关系原理对线段进行初始匹配。设空间点X 在各视图中的重投影点为xi＝PiX，Pi是第i幅视图的相机矩阵。定义视图i中的线段lia与视图j 中的线段ljb存在弱匹配关系，当且仅当两线段关联相同的空间点X，即存在空间点集η R3使得η＝｛X｜xi＝PiX，xj＝PjX，xi∈lia，xj∈ljb｝。

记outX 为关联空间点X 的线段集合，根据弱匹配关系原理，该集合内的线段存在弱匹配关系。记outl为重投影点属于二维线段l 的空间点集合，这些空间点应在同一条三维线段上，因为l是这条三维线段的投影。

图1为3个视图间线段的匹配情况。空间点Xb和Xc在视图B中的重投影点都属于lb，在视图C 中的重投影点都属于lc，所以outXb＝outXb＝ ｛lb，lc｝，outlb＝ ｛Xa，Xc｝，lb与lc存在弱匹配关系。三维空间点重投影回视图后变为二维平面点会造成深度信息丢失，上述的线段匹配方法将产生许多误匹配。如空间点Xa和Xb在视图C 中的重投影点重合且属于同一线段lc，但视图C 显然不能观察到空间点Xa；若在视图A 中Xa的重投影点被检测属于la，则会造成la与lc误匹配，这将不利于后续的三维线段生成。为解决深度信息丢失问题，必须得到有哪些视图可以观察到该空间点的信息，记visXi为空间点Xi的可视视图集合，该集合内的所有视图均可观察到Xi。本文使用修改后的PMVS［11］软件生成每个空间点的可视视图集，同时生成密集点云。

生成outXi时，为避免由于深度信息丢失而造成线段误匹配，只将Xi投影到visXi包含的视图中，然后在各视图中检查重投影点是否属于某一线段，并将符合条件的线段加入outXi。为生成outlia，只需在线段lia加入outXi时，将空间点Xi加入outlia。

图1 多视图间线段匹配

2.2.2 筛选匹配

上述线段弱匹配关系存在大量误匹配，必须进行筛选，形成正确的线段匹配关系。对一条三维线段，可由在此线段上的空间点X 的outX 得到在各视图中具有弱匹配关系的二维线段，而此三维线段上的所有空间点可提供各视图中匹配线段的统计信息。对这些线段的匹配次数进行统计，在各视图中选取匹配次数最多的线段为该视图中正确匹配的线段。记Θ 为计算得到的所有匹配线段组的集合，计算Θ 的步骤如下：

步骤1 取outlia中的一个空间点Xi，将outXi中所有二维线段的匹配计数加1。

步骤2 对outlia中的所有空间点重复步骤1，得到与lia存在匹配关系的所有二维线段的匹配计数。二维线段ljb的匹配计数代表视图j 内的ljb与视图i内的lia的匹配程度。

步骤3 在视图j中，取匹配计数最大即匹配程度最高的线段为该视图中唯一与lia匹配的线段。

步骤4 在所有视图中重复步骤3，获得n 个视图中与lia匹配的n 个线段组成的匹配线段组s，并将s中的所有线段标记为已匹配。

步骤5 更新Θ 为Θ：＝Θ∪s。

步骤6 对所有标记为未匹配的二维线段，重复执行上述步骤1～步骤5，即可获得匹配线段组集合Θ。

2.3 三维线段生成

平面交线法［5］反投影匹配线段生成多个反投影平面，然后用SVD 分解确定这些反投影平面的公交线。SVD 分解本质上是最小二乘法，最小二乘法的缺点是对噪声比较敏感，当出现线段检测误差和误匹配线段时，线段模型会出现较大的重建误差，产生大量杂线。

为解决上述问题，本文采用空间直线与空间平面相交法计算候选三维线段，并参考RANSAC算法滤除外点，稳健估计模型参数的思想准确计算三维线段。

从匹配线段组中任意选取一对匹配线段，计算一条候选三维线段。将三维线段重投影回匹配线段组对应的各视图中，评估各视图中重投影线段与原始匹配线段的重合程度。若在大多数视图中，重投影线段与原始匹配线都重合，则此三维线段的重建精度较高。而杂线的重投影线段在大多数视图中与原始匹配线段都不重合。一条候选三维线段的重合次数越大代表它的重建精度越高。根据上述方法计算匹配线段组内所有可能的一对匹配线段的候选三维线段和它的重合计数。取重合计数最高的三维线段为该匹配线段组对应的三维线段。

2.3.1 估计候选三维线段

本文采用空间直线与空间平面相交法计算三维线段端点。如图2所示，l1经过摄像机P1反向投影得到平面π1＝P1l1，l2的端点e21经摄像机P2反向投影得到的直线与π1相交得到三维线段L 的一个端点E21，同理得另外3个端点E22，E11，E12。由于线段端点不能精确匹配，L 的端点不能精确计算，本文采取的策略是在这4个候选端点中选取其中两个使L 的长度达到最长。如图2中选取E21，E12为L的端点。

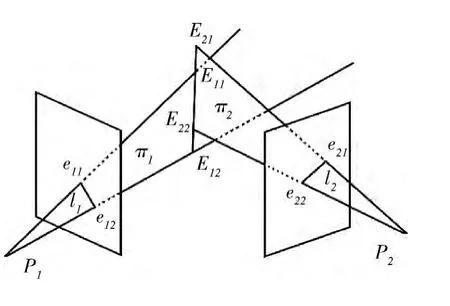
图2 估计三维线段

为计算反投影直线与反投影平面的交点，设视图的摄像机矩阵为P＝ ［M ｜p4］，则摄像机光心为C＝ （－M－1P4，1）T。视图中一点x被摄像机反投影形成的射线L 交无穷远平面于点D＝ （（M－1x）T，0）T，由D 和C 可将投影射线L 定义为点束

射线L（φ）与平面π的交点L（φX）必在平面π上，故有πΤL（φX）＝0，代入式 （1）得

可解出

将式 （3）带入式 （1）即可求出交点L（φX）。

2.3.2 计算候选三维线段的重合计数

为判断候选三维线段L 是否为重建误差较大的杂线，首先将L 重投影到匹配线段l 所在的视图中，得到重投影线段lp。当同时满足以下3个条件时判定l与lp重合。

（1）l两端点到lp的距离小于阈值d；

（3）lp与l之间夹角小于阈值θ。

将L 重投影回匹配线段组对应的各视图中，并累计L的重合计数。若重合计数太小，表明候选三维线段存在较大的估计误差，而重合计数越大表明候选三维线段的重建精度越高，所以仅保留重合计数最大的三维线段，并记与此三维线段重投影线段重合的匹配线段集为visL，该集合基本滤除了重投影误差很大的误匹配线段。

2.4 三维线段模型优化

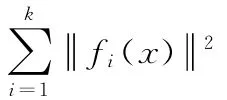
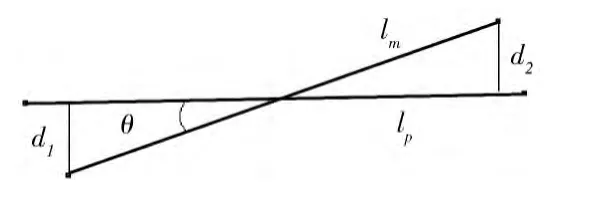
图3 三维线段重投影误差

本文使用ceres－solver［12］求解这个非线性最小二乘问题，优化调整所有三维线段，进一步减小三维线段的重投影误差，提高模型的重建精度。

3 实验结果及分析

我们使用无人机对城市某一范围内建筑物场景进行航拍，采集了141 幅6000＊4000 的图像。实验环境为Intel Xeon E3－1230v2，16GB内存，编程环境为Visual Studio 2010。

为验证本文线段匹配算法的有效性，我们对图4和图5所示的两个图像对进行线段匹配，并与文献 ［4］的方法（RLM）进行比较，文献 ［4］的实验结果表明，RLM 的性能相比MSLD［2］和Line Signature［3］均有提高。RLM 算法实现代码由作者提供。为加快实验进度，减少线段数量，我们将图像降采样至1500＊1000分辨率。

表1图像对一栏括号内的数字是两幅图像检测出的线段数量，算法栏括号内数字分别是匹配线段数，正确匹配线段数和匹配正确率。本文算法和RLM 算法均使用LSD提取线段。

图4 图像对a

图5 图像对b

表1 线段匹配结果

图像对a的两幅图像视角变化不大，两种算法都有较高的正确率，但本文算法正确匹配线段的数量较多。图6左侧和右侧分别是RLM 算法和本文算法在同一区域的线段匹配结果，可见本文算法的匹配线段更密集。因为RLM 用落在线段附近支持区域内的稀疏SIFT 特征点确定线段的匹配关系。而本文使用的密集点云重投影点比SIFT 特征点数量多且稠密，有更多的点落在线段支持区域内，所以检测匹配线段数量有较大提升。

图6 线段匹配结果

图像对b的两幅图像视角变化较大，两种算法的匹配线段数量和正确率均有下降，但RLM 算法的下降幅度更大。因为在视角变化较大时SIFT 算法无法产生足够数量的匹配点；建筑物边缘处线段的支持区域在不同视角下变化很大，两个变化较大视角有可能只观测到线段不同侧的支持区域。本文算法不利用线段附近支持区域内特征点或灰度信息，而是利用关联同一三维点的重投影点确定线段匹配关系，所以对较大视角变化不敏感，仍能达到较高的检出率和正确匹配率。

为验证本文的三维线段重建算法，先用Bundler［13］生成稀疏点云模型和摄像机矩阵，然后使用修改过的PMVS生成密集点云和可视视图信息。图7为由图像生成的密集点云模型，该模型的建筑物主体出现了的空洞，且未能良好体现建筑物规整的结构特征。本文算法生成三维线段模型时，将重投影线段与匹配线段间夹角阈值θ设为5°，匹配线段端点到重投影线段的距离阈值d 设为两个像素，线段长度比例阈值δ 设为0.25。最后根据重建结果与文献［5］和文献 ［6］的方法进行比较分析。

图7 密集点云模型

如图8所示，本文算法能完整体现建筑的整体框架和直线边缘，很少出现因误匹配和错误重建产生的杂线，表明本文算法能有效应对线段的误匹配和测量误差，滤除重建误差较大的杂线，稳健性强。模型准确还原了建筑物表面具有直线特征的窗户和广告牌位，线段端点没有出现过长的冒头和过短的断续，建筑物边缘清晰锐利，模型的细节部分也得到了良好体现，表明最后的优化调整算法确实能有效提高重建精度。

图8 本文算法重建结果

文献 ［5］提出平面交线法生成三维线段模型。由于最小二乘法对噪声敏感，且算法在生成三维线段时没有滤除误匹配线段，造成初始重建的三维线段模型充斥大量杂线，淹没了建筑物的主体结构，必须用长度约束和角度约束滤除杂线。经过实验调整，我们将文中提到的阈值d0设为0.2，d1设为15，d2设为4。设定阈值这项工作只能由人工依据特定场景的视觉效果逐步调整，不同的场景需要不同的阈值，未能实现完全自动化，且有很强的主观性。而本文算法的自适应性强，不用根据特定场景调整阈值，无需人工干预，实现了自动化重建。重建结果如图9 所示，建筑物边缘处仍有很多短小的杂线，未能体现清晰的边缘特征。因为全局的长度约束和角度约束无法滤除符合约束的杂线，而且有可能滤除正确重建但不符合约束的三维线段。

图9 文献 ［5］重建结果

文献 ［6］没有使用匹配线段和摄像机参数计算三维线段，而是选定点云内某些三维点作为三维线段的端点，虽然速度很快，但三维线段模型完全依赖于密集点云模型，容易受到点云疏密的影响。如图7和图10所示，高楼的密集点云模型在主体位置出现空洞，三维线段模型在同一位置也出现空洞。模型边缘的线段也不够整齐锐利。因为在边缘处点云并非规整平直的分布在一条直线上，甚至存在许多外点，以这些点作为三维线段端点无法达到更高的精度。本文算法生成三维线段模型时不依赖密集点云，所以模型结构完整，未出现空洞。

图10 文献 ［6］重建结果

4 结束语

本文针对建筑物的三维线段模型重建，提出了基于密集点云重投影的多视图线段匹配算法，该算法匹配准确度高，且对差别较大的视图变换具有较强的鲁棒性。稳健的三维线段生成算法能有效处理误匹配线段和端点检测误差，减少杂线的产生。模型优化调整算法可最小化三维线段的重投影误差，提高模型的重建精度。实验结果表明，本文算法重建的建筑物三维线段模型能完整体现建筑物的框架结构和规整的直线边缘，具有良好的视觉效果。在后续工作中，我们将利用本文算法提供的三维线段模型对建筑物网格模型进行优化调整，以期得到边缘更规整，视觉效果更好的建筑物网格模型。

［1］Bay H，Ferrari V，Van Gool L.Wide－baseline stereo matching with line segments［C］／／Proceedings of the IEEE Computer Society Conference on Computer Vision and Pattern Recognition，2005：329－336.

［2］Wang Z H，Wu F C，Hu Z Y.MSLD：A robust descriptor for line matching ［J］.Pattern Recognition，2009，42 （5）：941－953.

［3］Wang L，Neumann U，You S.Wide－baseline image matching using line signatures ［C］／／Proceedings of the IEEE international Conference on Computer Vision，2009：1311－1318.

［4］Fan B，Wu F C，Hu Z Y.Robust line matching through linepoint invariants ［J］.Pattern Recognition，2012，45 （2）：794－805.

［5］ZHANG Linyan，ZHU Li.3Dline segments reconstruction for building facades with line matching across multi－image with nongeometry constraint［J］.Journal of Xi’an Jiaotong University，2014，48 （4）：15－19 （in Chinese）.［张琳彦，朱利.以多幅图像非几何约束线段匹配重建建筑物外立面三维线段模型［J］.西安交通大学学报，2014，48 （4）：15－19.］

［6］Chen T W，Wang Q.3Dlinesegment detection for unorganized point clouds from multi－view stereo ［C］／／Proceedings of the Asian Conference on Computer Vision.Berlin，Germany：Springer－Verlag，2011：400－411.

［7］Hofer M，Wendel A，Bischof H.Line－based 3Dreconstruction of wiry objects［C］／／Computer Vision Winter Workshop，2013.

［8］Hofer M，Wendel A，Bischof H.Incremental line－based 3Dreconstruction using geometric constraints［C］／／British Machine Vision Conference，2013.

［9］Fischler M A，Bolles R C.Random sample consensus：A paradigm for model fitting with applications to image analysis and automated cartography ［J］.Communications of the ACM，1981，24 （6）：381－395.

［10］Gioi V，Grompone R.LSD：A fast line segment detector with a false detection control［J］.IEEE Transactions on Pattern Analysis and Machine Intelligence，2010，32 （4）：722－732.

［11］Furukawa Y，Ponce J.Accurate，dense，and robust multiview stereopsis ［J］.IEEE Transactions on Pattern Analysis and Machine Intelligence，2010，32 （8）：1362－1376.

［12］Agarwal S，Mierle K.Ceres solver ［CP／OL］.http：／／ceres－solver.org，2010.

［13］Snavely N，Steven M S，Szeliski R.Photo tourism：Exploring image collection in 3D ［J］.ACM Transactions on Graphics，2006，25 （3）：835－846.