搜索引擎方法在实时地震监测中的应用＊

Jie ZhangHaijiang ZhangEnhong ChenYi ZhengWenhuan KuangXiong Zhang

1）Laboratory of Seismology and Physics of Earth’s Interior，School of Earth and Space Sciences，University of Science and Technology of China，Hefei 230026，China

2）School of Computer Science and Technology，University of Science and Technology of China，Hefei 230027，China



搜索引擎方法在实时地震监测中的应用＊

Jie Zhang1）Haijiang Zhang1）Enhong Chen2）Yi Zheng2）Wenhuan Kuang1）Xiong Zhang1）

1）Laboratory of Seismology and Physics of Earth’s Interior，School of Earth and Space Sciences，University of Science and Technology of China，Hefei 230026，China

2）School of Computer Science and Technology，University of Science and Technology of China，Hefei 230027，China

摘 要当地震发生时，地震学家需要利用记录的地震图尽快去推断震中、震级和震源机制解。如果能快速判定这些信息，就能进行及时疏散，并采取应急措施以减轻地震灾害。现在有一些先进的方法能在地震后几秒内判断出最初的震中和震级，但可能需要数分钟到几小时才能估算出震源机制解。这里我们提出针对大型地震图数据库，利用一种类似于互联网搜索引擎的地震搜索引擎方法，来寻找输入地震波数据的最佳匹配。该方法比当前的精确查找法快几千倍。以2012年3月8日新疆MW5.9地震为例，该搜索引擎方法能在长周期地震面波到达后1s内推算出地震震源机制参数。

关键词搜索引擎方法；实时地震监测；震源机制解

引言

在地震学界，实时地震信息发布早已是一项重要的研究工作［1－3］。近几年，地震预警系统的发展进一步推动了此项工作的研究步伐，其能在地震发生后数秒到1min左右向公众发布预警信息［4］。全世界已有一些地震预警系统正在实施应用中，包括日本的紧急地震速报系统（REIS）［5］，墨西哥的地震预警系统（SAS）［6］，中国台湾的地震预警系统（VSN）［7］和土耳其的地震预警系统（IERREWS）［8］。在美国加州，开发的ElarmS预警系统已被列入一项重要的研究计划，该系统已进行了离线测试，但尚未完全部署［4］。地震学家已研制出可靠的算法用于自动估算地震的震源信息［9－10］。例如，日本REIS系统通过利用来自密集监测网的数据，在P波到达后5s内推算出震中和震级［5］。然而，即使是利用最近发表的新方法，在地震可能发生的位置网格点上提前计算好格林函数，然后利用格林函数反演矩张量，仍然需要几分钟甚至更长时间才能获取震源机制解［11－13］。利用GPS数据进行相似的研究工作也只能在几分钟内确定大地震的矩张量［14－15］。

除了震中和震级外，实时获取震源机制解也同样重要。例如，海啸预报需要完整的震源参数，包括震源深度、震级和断层滑动走向等［16］。2010年10月5日发生在苏门答腊岛西海岸的MW7.7浅源地震，导致当地发生了海啸，浪高达到3m，几分钟内影响了整个岛屿。据报道，死亡人数超过400人［17］。震源机制解研究表明，这次地震属于逆断层运动，从而造成海水运动。相比较，2012年4月11日在印度洋发生了MW8.6大地震和随后的MW8.2余震，尽管在印度洋海域发布了海啸预警，但最终并未形成海啸。通过震源机制解研究表明，这两次地震都是顺着走向滑动造成的［18］，因此垂直向运动位移相对较小，不足以形成海啸。震源机制解的实时估算对于监测断层活动也非常重要。例如，Bouchon等［19］对1999年伊兹米特MW7.6地震进行了研究，发现其一系列前震的震源机制解表明在断层加速运动至破裂过程中存在相似的断层滑动。实时获取震群的震源机制解可能有助于识别断层活动特征。这类信息能让我们快速发现地震活动区并实时跟踪断层运动。

当前的挑战为，当一些台站收到地震数据后几秒内必须自动快速估算出震源机制解。我们开发了一种基于图像的地震搜索引擎，类似于互联网搜索引擎，在一个单一的AMD工作站的大型数据库中搜索相似的地震波形图，在1s内估算出地震震源机制参数。计算机搜索技术的重要发展有助于促进文字、图像、视频和来自网络尺度数据集的音频等搜索行业的发展［20－32］。与录音和一维图像相似，一幅地震波形图可认为是地震台根据时间记录的地面运动情况，其包含的信息包括震源和地下介质。通过假设已知地球速度模型，我们采用正演模拟方法，在离散的网格点上为可能的地震震源机制和震中位置构建波形数据库。我们的目标是，对于任何一个新的地震记录，都能从数据库中找出最佳匹配。这个方法是完全自动的，不需要输入任何参数或人工干预。因此，它可以用于通常的地震参数报告。

我们利用在新疆试验区中的3个地震实例测试我们的地震搜索引擎法。我们选择了一个经纬度5°×5°的区域构建一个快速搜索数据库。3个地震事件发生后，通过搜索引擎法在收到长周期面波数据后1s内，都可以得到搜索结果。在数据库覆盖范围内的任意单个地震事件，都可以得到足够精确的震源参数。如果单个地震事件发生在数据库覆盖范围以外，或者是多个事件相继发生在邻近区域，搜索引擎能自动通过预设的互相关阈值排除无效的结果。

1　计算结果

1.1 用于新疆试验区的搜索引擎数据库

图1显示在南疆一个5°×5°的试验区，3个固定地震台（暗红色三角）能记录5°～15°范围内的地震事件。这些台站包括MAKZ （46.8°N，82.0°E，哈萨克斯坦马坎奇），KBL（34.5°N，69.0°E，阿富汗喀布尔）和LSA（29.7°N，91.1°E，中国拉萨）。从2000 年1月1日至今，根据美国地质调查局（USGS）国家地震信息中心（NEIC）的记录，在试验区内共发生MW4.0以上地震51次。

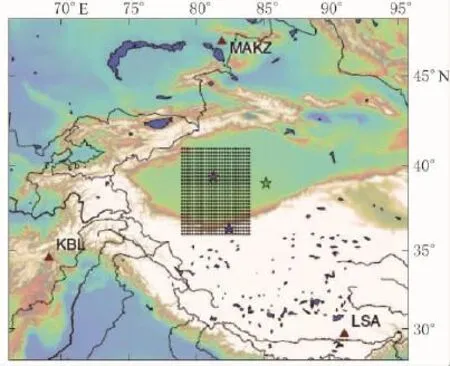
图1　地震台站和虚拟试验区的位置。

在3个以暗红色三角形所标示的地震台站区域范围内（MAKZ：46.8°N，82.0°E，哈萨克斯坦马坎奇；KBL：34.5°N，69.0°E，阿富汗喀布尔；LSA：29.7°N，91.1°E，中国拉萨），由虚拟震源构建大型合成数据集，创建一个快速搜索数据库。3次地震由星形标示（其定位信息均由美国地质调查局的国家地震信息中心提供），用于测试不同的状况。紫色星代表2012年3月8日发生的MW5.9地震；蓝色星代表2011年9月15日发生的MW5.3地震；绿色星代表2014 年4月30日发生的MW5.3地震在本研究中，我们着重于对研究区内小震和中震的实时分析，以确定它们的震源和双力偶震源机制解。我们的方法包括以下几步：①构建格林函数综合数据库，在横向均匀介质中设置离散网格节点，计算每个节点作为虚拟震源的格林函数，计算时考虑所有可能的双力偶源解；②在数据库中利用主成分分析法（principal components analysis，PCA）减少时间采样点个数；③利用互联网工业发展的快速搜索算法，快速找出最佳匹配的虚拟源；④对震源机制解的确认和搜索结果分辨率的定量化。

为了设计一个用于监测试验区的地震搜索引擎，我们构建了一个包含大量合成地震记录的数据库，这些记录与试验区内3D网格上的每个虚拟源相一致。我们的三分量地震图计算采用Thompson－Haskell传播矩阵技术在多层半空间的地震点源弹性波模型［33］。在这个研究中，我们首先关注试验区内5°～15°范围内的浅源地震，通过模拟一些研究区的历史地震测试PREM地球模型［34］。在区域内利用该模型模拟长周期地震波（0.01～0.05Hz）的传播是合理的。我们也利用试验区内和试验区外的真实地震事件测试了搜索引擎，同时也测试了2个真实地震构造的假设双震事件。

如图1所示，试验区为36°N～41°N，79°E～84°E，间隔为0.2°。深度网格从5～60km，间隔为5km。因此，在这个3D网格中大约有8 112个虚拟源。每个网格点的震源机制解离散如下：走向范围从10°～350°，间隔为20°；倾角范围从5°～80°，间隔为15°；滑动角范围从－170°～170°，间隔为20°。这样，在每个虚拟源共形成1 944个不同的事件。因此对于一个地震台来说，我们都能产生15 789 168（8 122×1 944）三分量地震图用于3D网格上的地震事件，也就是说，总共有47 367 504个三分量地震图用于这3个地震台。为构建搜索数据库，我们将3个地震台的所有三分量地震图进行融合，并为每个虚拟地震构建一个长的超级道（supertrace）。因此，在每个搜索数据库中共有15 789 168条超级道。

对于任意虚拟源位置，计算量最大的是在卷积震源机制解之前震源和接收器之间的格林函数的计算。对于一维地球模型来说，应该有9组格林函数，其中8组能用于计算双力偶源的三分量地震图［13，33］。幸运的是，格林函数不依赖于震源机制解，因此，我们仅需要计算每个网格点的一组格林函数。

此外，我们提出一个内插方法，用于有效地计算离地震台任一给定距离位置的理论地震图。这个方法可以大大降低搜索数据库构建的计算量，且精度可以接受。图2对内插方法进行了图解说明。以地震台为中心，以一定的插值间隔画实线圆，同时，以实线圆为中心在两边画虚线，标记插值区域。在地球变平换算后的任何一个插值间隔内，我们对与实线圆一致的震中距上的唯一一个虚拟源计算格林函数。对于在3D网格上相同

图2　一种用于准备搜索数据库的插值方法。

针对一个地震台，定义了具有一定间隔的实线圆。对于实线圆上的虚拟源，利用一维地球模型计算合成格林函数。对于落在两条相邻虚线之间相同间隔的网格点，利用与那些位于中央实线的点相同的格林函数作为近似值，如此可减少计算时间深度的任何虚拟源，如果它位于相同的间隔，那么它将被分配相同的格林函数作为近似值。在这个研究中，我们的震中距范围是5°～15°。如果我们选择0.2°作为间隔，这意味着我们仅必须为600个（50间隔×12深度）虚拟震源计算地震图，而不必考虑台站数量，与24 366（8 122×3台站）个虚拟源相比，最高能降低40%计算工作量。在单个工作站上，在新疆试验区进行地震图计算构建数据库需要花费大约13h，产出15 789 168个超级道并构建树形结构用于快速搜索还需要再用30min。因此，如果有高性能的计算资源，创建一个智能搜索数据库是一个非常有效的方法。

1.2 快速搜索结果

在新疆试验区，2012年3月8日发生了MW5.9地震（图1中紫色星所示）。根据全球矩张量解（CMT）记录［35］，该地震事件发生在39.49°N，81.47°E，深度44.4km。我们利用此事件作为输入，用我们提出的地震搜索引擎来确定其震中和震源机制解。此外，我们选择2个其他地震用于特殊事件的系统测试。这些事件包括2014年4月30日发生的MW5.3地震，位于43.02°N，94.26°E，深度10.0km（图1中绿色星所示；根据NEIC地震目录，地震位于试验区外［36］），以及发生于2011年9月15日的MW5.3地震，位于36.32°N，82.50°E，深度11.6km（图1中蓝色星所示；根据NEIC地震目录，地震位于试验区内［36］）。对于发生在2011年9月15日的地震来说，我们将整个事件的发生时刻进行平移，来模拟其在2012年3月8日地震后40s发生的情况。通过两个地震重叠构建人为的双震记录。我们的搜索数据库并未专门考虑双震或多震事件。然而，人造的双震记录可用于测试我们的搜索引擎方法如何处理此类事件。

图3显示了2012年3月8日地震输入数据的超级道（上部红线）以及数据库中从1 到1 000，每间隔100的最佳匹配。由于每个超级道是由3个地震台的三分量数据融合而成，而我们的搜索是基于从相似的事件中匹配9个可用的全波形。在图3中，最佳搜索结果显示的震源机制解，与全球矩张量解相

图3　输入数据和前1 000个搜索结果。

利用全球矩张量结果（红色）将3个地震台的数据与前1 000个搜索结果中每间隔100的结果（黑色）进行比较。左边为震源机制解序列索引和最大互相关值，右边为震源深度、经纬度和震源机制解

利用全球矩张量结果（红色）将3个地震台的数据与前10个搜索结果（黑色）进行比较。左边为震源机制解序列索引和最大互相关值，右边为震源深度、经纬度和震源机制解似，震源位置与全球矩张量解记录相比，水平偏差15km，深度偏差0.6km。前200个结果表明，与全球矩张量解相比震源位置偏差在25km内，震源深度偏差在5km内。图4显示了在1 000个结果中的前10个最佳匹配结果。在所有10个搜索结果中的震源机制解都与全球矩张量解结果非常接近。

在10个最佳结果中，最大的互相关系数从0.869 5下降到0.862 6，变化很小，意味着这些结果存在非唯一性，这可能是受到有限的数据和观测站几何分布的影响。由于它定义了该结果的信度水平，因此了解这种情况非常重要。无论如何，这些结果表明震中位置、震源深度和震源机制解都能合理地包含在这个事件中。在这一特定的地震事件中，震源深度和震源机制解的估算可能比震中位置的估计更为可靠。

图5显示了在测试网格中震源深度为45km的最佳匹配结果，同时给出了全球矩张量解定位的输入事件（紫色星）。在每个网格点，图中表明了与输入事件最佳匹配的震源机制解，且具有最大的互相关系数。我们的最佳搜索位置与全球矩张量解的经纬度相差约半个网格（0.1°）。绘制像图5中不同深度的震源机制解，能帮助我们理解在三维空间中解的不确定性。

图6表明在最佳匹配位置下，矩张量解和最大互相关系数与深度的关系。虚线为我们的最佳估计震源深度是45.0km，而全球矩张量解的深度为44.4km。这两个结果相当接近，意味着我们的结果与全球矩张量解一致。

图7显示了最佳的1 000个搜索结果的最大互相关系数曲线。该曲线给出了搜索结果非唯一性的直接说明。如果曲线随着结果快速下降，意味着能很好地得到最佳结果。否则，表明存在太多的非唯一的或近似的结果。在这个研究中，褐色曲线快速下降，因此，该结果的信度水平很高。

我们也利用了2014年4月30日发生在试验区外的地震测试搜索引擎。图7中显示，蓝绿色曲线代表该事件中最佳匹配的1 000个搜索结果的最大互相关系数，所有的最大互相关系数都小于0.40，这是一个非

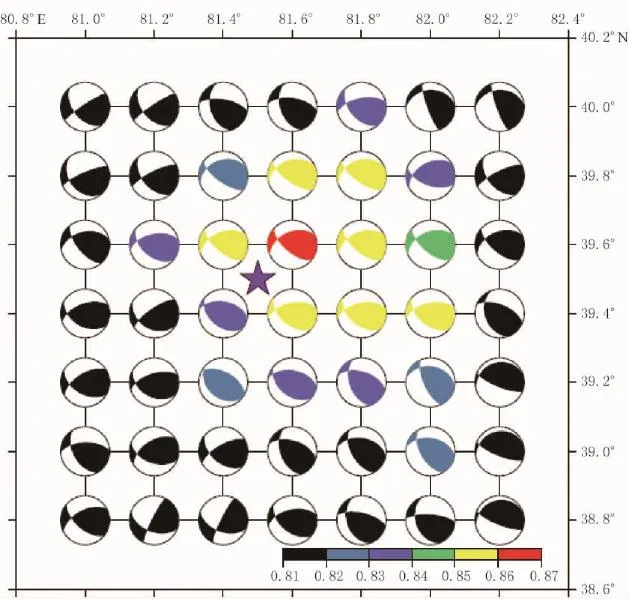
图5　地震横向定位不确定性。

对于震源深度为45 km，输入值和搜索结果之间的最大互相关值的分布，以及最优匹配结果的震源机制解。紫色星标记为全球矩张量解的定位结果。彩色比例尺表示最大互相关值的范围

图6　震源深度不确定性。

曲线表示在最优匹配结果的地面点，震源深度在5～60 km，输入数据和搜索结果之间的最大互相关值。实线表示全球矩张量结果震源深度为44.4 km的值，虚线表示快速搜索法的最优匹配结果为震源深度45 km常低的值。这主要是因为在3个地震台的搜索数据集中不能找到与发生在试验区外地震相匹配的波形。同样地，图7中的橘色曲线表明，双震的搜索也出现很低的互相关系数。通过利用人工和真实数据的实验，我们发现互相关系数0.7是该系统在特定区域判别无效结果的阈值，包括地震发生在搜索数据集覆盖范围以外、多个地震叠加以及复杂破裂过程的大地震等情况。这意味着地震搜索引擎可以自动判别结果的有效性，避免错误报告。在这些测试事件中，当输入值与搜索结果的最大互相关系数低于0.7时，这些搜索结果被认为是无效的。该研究结果意味着任何的已有搜索数据库都应该进行更新，或者采用不同方法来更新数据。对于不同的区域和监测台网，在应用该系统前，都必须

图7　三次地震测试搜索结果的比较。

实线表示输入数据和前1 000个搜索结果之间的最大互相关值。褐色曲线表示试验区内2012年3 月8日发生的MW5.9地震的结果。蓝绿色曲线表示试验区外2014年4月30日发生的MW5.3地震的结果。橘色曲线表示由2012 年3月8日地震和2011年9月15日MW5.3地震构建出虚拟双震的结果。虚线表示用于验证搜索结果的互相关阈值进行重新估算和设置阈值。如果搜索数据库可以包含特殊事件，搜索引擎方法应该能用于处理不同事件。我们应该探讨许多可能性来改善数据库。

2　讨论

通过新疆测试区我们已经表明，利用地震搜索引擎，在收到长周期面波后1s内，我们能给出地震震中位置、震源深度和震源机制解。但不只是一个解，搜索引擎真正得到的是近似结果的子集，它也能帮助我们在1s内来评估结果的信度水平。这项研究对于震源机制解的快速估算是一个重要的改进，它对于开展海啸预警和监测大型断层活动更加有效。在这个研究过程中，我们并未探讨震级参数。这是因为震级可以直接利用振幅信息进行估算［37］。

这个新方法需要在局部或者监测区域范围内为试验区构建一个搜索数据库。我们的正演模拟计算仅限于点源，因此这个研究以震级小于7.5级地震为对象。然而，我们的搜索引擎并不会局限于特定震级大小或波谱类型。如果我们能构建一个包含模拟的大地震信息的数据库，那么搜索引擎就能找出最佳波形匹配值，并能获取地震震源机制参数。对于大地震的动态破裂过程来说，构建这样一个搜索数据库可以说是一个挑战，也是很复杂的工作。可能的解决方案包括，考虑震源规模对中低频数据予以适当权重［2］，近似有限源格林函数合成计算［12］，以及利用最大方差缩减方法从搜索结果中定义震中位置［15］。一些地震确实在历史上重复出现，在地震活跃区，利用历史地震的震源信息构建一个数据库，也将是一个值得关注的途径。

我们的研究主要采用低频面波作为输入数据。对于局部或整个区域范围内，利用相对准确的三维速度模型，例如南加州，地震搜索引擎在该地区就可利用高频体波。在研究中，由于体波能合理地利用格林函数进行估算，地震搜索引擎能在收到地震信息后的1s内利用P波初动，快速得到震源机制解（包括震中和震级）。对于宽频带或高频数据，可考虑利用人工合成输入数据校准P波到时信息。幸运的是，在数据库中校准无噪声地震合成记录相对容易。对于输入数据，我们简单地对于P波到时采用一系列较小的正负偏移，并同时利用所有原始记录和偏移记录进行快速搜索。我们选取与最小误差值相关的结果作为最后的结果。这个方法有助于消除P波到时不准确的影响。

在这个研究中，我们在新疆选择了一个5°×5°的范围，震源深度在5～60km，在单一的CPU计算机上测试我们的地震搜索引擎。如果我们在空间上扩大研究区范围，或对虚拟源和局部结果减小网格插值间隔，搜索数据库也将增加更多信息。我们用于计算格林函数的插值方法表明，对于合成数据集来说，计算时间仅仅与震中与台站间的距离相关；因此，密集台站或者监测网并不会显著增加计算时间。考虑到不同频率体波和面波的相关数据信息的重要性，我们根据同一地震不同数据信息，设计了多线程搜索方式，以确保结果的可靠性。我们也通过采用搜索引擎法实时对波形数据进行分组，并在数据接收过程中对结果进行不断更新。我们将进行进一步的研究工作。

3　方法

3.1 计算机快速搜索技术

在本研究中，地震搜索引擎利用类似于网络搜索引擎的快速搜索方法，后者主要用于在网络上查找以文字为主的信息，大量的搜索结果以索引和归类的方式存放于一个大型数据库中［20］。图像搜索引擎与其类似，但它是基于图像的，并对内容以及其他信息进行相似性评估，用于获取与记录图像的最优匹配值［21－23］。网络技术已经激发其他领域的相关研究，例如，Aguiar和Beroza［38］应用网络排序方法分析地震波的相似性。

在计算机搜索领域，数据中的大量采样点被作为它的“维度”。地震图的相似性搜索是一个高维问题，需要努力地从大型数据集中搜索真正的结果。降维法能在保持数据本质特征的同时，有效地减少时间样本的数量［39］。除了降维以外，一个重要的方法是近似临近搜索法，它能比精确查找快很多，而且能提供近似最优精确度［24］。

已有的快速搜索方法多是基于散列结构或树结构，例如区域敏感散列结构［25］和多重随机K维树方法（MRKD）［26－27］。通过利用这两种方法处理地震图，我们发现MRKD树结构方法用于处理高维地震图数据集的变化始终很快。Silpa－Anan和Hartley［26］及Muja和Lowe［24］认为，MRKD树方法能很好地处理计算机视觉中的高维数据集问题。这个方法通过在树结构的每一层上将振幅变化最大的波形数据拆分成两半，从数据集构建多重树结构。数据库利用有限样本获取地震数据中最重要的特征，然后当有记录到达时，我们根据树结构搜索最优匹配结果。这个方法需要通过log2N次计算比较，从一个树结构中找出第一个候选作为最优匹配结果，N代表数据库中地震图的数量［28］。如果需要更多的搜索结果，则需要附加的回溯工作。

3.2 利用MRKD树对地震图进行索引和分类

图8举例说明了如何利用数据库中虚拟的4个地震图构建K维树。4个地震图的初至波被记录下来并对齐排列。在每个时间样本中，计算4个地震图的振幅平均值。图8a的最下面一条曲线显示了每个时间样本振幅与平均值的方差。最大的振幅方差为0.143，平均值为0.176，从树结构中挑选出的是第864个采样点（维）。选择相同的时间样本，振幅比平均值小的地震图（ID＝1，4）放置于维节点的左侧，而那些振幅大于平均值的地震图（ID＝2，3）位于右侧。上述进程被递归式地用于左右单独排列的地震图，到任意维节点下仅留下一个地震图（叶节点）为止。

图8b显示了在以上进程后形成的二级树。实际上，应该利用同一数据集构建多重随机K－D树并用于搜索。为构建多重树，我们可以利用Muja和Lowe的方法［24］，从前m个具有最大方差的维中随机地选择一个分离维。在我们的应用程序中，利用固定值m＝5，从一个大型地震数据集中构建了128个树。当需要查询的地震图输入时，相同维（时间采样点）的数据集相对于平均值的振幅方差将与分区值进行比较，并用于确定哪一半数据属于查询数据。这个搜索过程是在所有树中分别进行的。在每个维节点，计算输入振幅值和数据集平均值间的累积L2距离值，同时通过增加L2距离值，保留所有随机树中单一的优先队列。在地震图ID有效的每个叶节点，计算输入和合成地震图之间

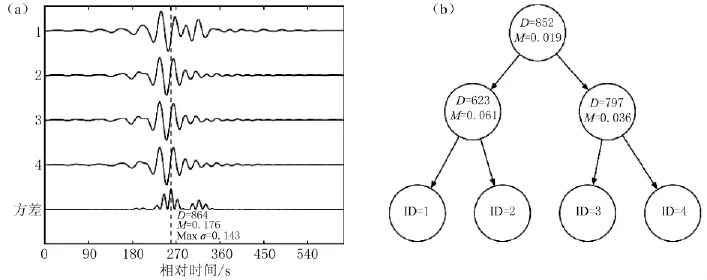
图8　快速搜索法标示地震波形。

MRKD树法用于构建快速搜索法数据库。（a）假设4个地震图的数据集，对于所有的道，计算每个数据维的平均值和RMS方差；（b）在树顶上，最大方差（0.143）出现在第864个样本，左边标示该样本的振幅值小于平均值（0.176），右边为那些大于平均值的样本。这个进程迭代地应用于每一层，直到每一边仅留下一个地震图为止的L2标准距离，并根据距离递增顺序保存在候选队列中。该算法需要迭代搜索来查找许多近似解。优先队列确定了用于下一次迭代对比的地震图，并且候选队列返回大量按照与输入地震图相似性递减顺序排列的结果［26］。该搜索方法是基于利用最高概率的理念，选择输入值的最相邻近似值。其原理在地震图匹配中是可行的，因为本质上对于真实地震图的精确匹配是不存在的，这是由于我们目前对于地球三维结构认知不完整，以及准确反演真实波传播效果的能力有限。

3.3 优化快速搜索性能

降维是加速搜索进程的另一个重要方法。其目标是识别数据模式及压缩模式下的数据表达，以突出数据的相似性和差异性。在各种降维方法中，主成分分析法（PCA）被认为是能可靠地将数据嵌入到低维线性子空间的好方法［39］。为了应用主成分分析法，我们首先计算数据集的协方差矩阵，然后求解其特征向量和特征值。对于n维的数据集来说，它应该有n个特征向量和特征值。如果我们仅选择p个具有最大特征值的特征向量作为投影基，那么最后数据集仅有p维，并不会损失太多信息。实际上，我们需要检查特征值的分布并确定p的最优值。

选择最优参数用于快速搜索方法非常重要。图9说明了我们如何选择树的数量，搜索结果的数量和主成分分析法的输入维，用于处理一个数据集中超过1 500万的合成地震图。图9a显示了在MRKD树中，返回的1 000个结果中搜索精度与树的数量的关系。搜索精度被定义为MRKD树与精确查找1 000个搜索结果的比值。对于128树来说，其精确度大约是76%，意味着在给出的1 000个结果中，760种快速搜索法的结果与该搜索法的精确搜索一致。该精确度应该足以用于选择最优波形匹配。图9b表示搜索前1 000个解的精度与搜索候选解个数之间的关系，其中用了5个不同的合成地震波形作为输入。在前1 000个结果中，更多的搜索返回值产出更多的精确结果，但其需要更多的计算量。看起来选择1 000个结果和128树能在精度和计算量之间达到一个好的平衡。对于以上的测试数据来说，原始记录包含3 072个时间样本（维）。图9c表明特征值与从数据协方差矩阵获取的维数的关系。该曲线可用于确定最优p值，并用于上述探讨的主成分分析法降维。该曲线表明，在100维以上的特征值非常接近于0。因此，可

图9　快速搜索法的最优参数估计。

搜索精度被定义为MRKD树与精确查找超过1 000个搜索结果的比值。虚线表示参数的选择。（a）为1 000个搜索结果的搜索精度与树的数量的关系。选择128树的精度约为76%。（b）为利用128树，前1 000个结果的搜索精度与基于5个不同合成地震记录测试搜索候选方案数量的关系。总共1 000个输出结果，足以达到约76%的精度。（c）为利用主成分分析降维后，数据协方差矩阵特征值与维数的关系。该曲线表明，大于100维的特征值非常接近于0，因此可以去除。新数据集的维数可降至100，且不会造成太多信息损失以去除这些与小的特征值相关的特征向量，而不会造成许多信息损失。选取100作为最优p值，新数据集的维数可降至100。

基于数据集概率的计算机搜索算法的性能差异很大［24］。对于三分量地震台站来说，我们首先使波形归一化，然后融合三分量数据生成每个事件的超级道。图10表明MRKD树法在未利用主成分分析法时，大约

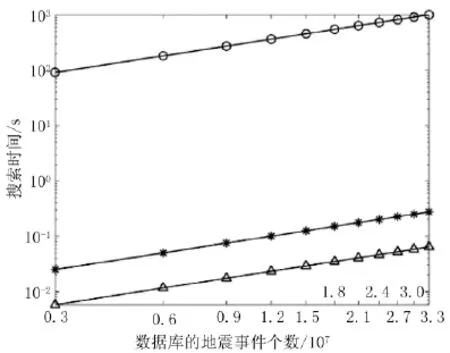
图10　不同方法下的计算机搜索时间对比。

对于返准L2需要超过17min来完成相同的工作。利用互相关查找最优匹配需要27h。这些测试都通过单一的AMD6136处理器进行。如上所述，MRKD树法在单一树需要log2N次对比来查找第一个候选用于最优匹配，N表示数据库中地震图的数量。然而，在图10中，MRKD树搜索时间与地震数量的关系在对数坐标系中几乎是线性的。这是因为我们实际上将数据集分割到多个更小的数据集，用于独立顺序检索，然后再合成结果。将来，数据集将构建成并行计算的形式。回的1 000个最佳匹配结果，在单一CPU上利用3种不同的方法进行测试。这些方法包括确定性线性搜索（圆圈标示），未进行降维的MRKD树法（星号标示）和利用主成分分析法降维的MRKD树法（三角形标示）需要0.2s在3 300万超级道输入值中查找1 000个最优匹配，而利用主成分分析法，仅需要大约0.06s。精确查找计算不匹配的标

资料来源：Zhang J，Zhang H，Chen E，et al.Real－time earthquake monitoring using a search engine method.Nature Communications，2014，5：5664.doi：10.1038／ncomms6664

（福建省地震局 王林 译，黄宏生 校；中国地震局地球物理研究所 王辉 复校）

（译者电子信箱，王林：wl＿0117＠163.com）

参考文献

［1］Allen R M.Seconds before the big one.Sci.Am.，2011，304：75－79

［2］Ekstrom G，Nettles M，Dziewonski A M.The global CMT project 2004—2010：centroid－moment tensors for 13017earthquakes.Phys.Earth Planet.Inter.，2012，200－201：1－9

［3］Satriano C，Lomax A，Zollo A.Real－time evolutionary earthquake location for seismic early warning.Bull.Seis.Soc.Amer.，1998，98：1482－1494

［4］Allen R M，Gasparini P，Kamigaichi O，et al.The status of earthquake early warning around the world：an introductory overview.Seismol.Res.Lett.，2009，80：682－693

［5］Nakamura H，Horiuchi S，Wu C，et al.Evaluation of the real－time earthquake information system in Japan.Geophys.Res.Lett.，2008，36：L00B01

［6］Espinosa－Aranda J M，Rodríquez F H.Mexico City seismic alert system.Seismol.Res.Lett.，1995，66：42－53

［7］Wu Y M，Teng T L.A virtual sub－network approach to earthquake early warning.Bull.Seis.Soc.Amer.，2002，92：2008－2018

［8］Erdik M，Aydinoglu N，Fahjan Y，et al.Istanbul earthquake rapid response and the early warning system.Bull.Earthquake Eng.，2003，1：157－163

［9］Horiuchi S，Negishi H，Abe K，et al.An automatic processing system for broadcasting earthquake alarms.Bull.Seis.Soc.Amer.，2005，95：708－718

［10］Kanamori H.Real－time seismology and earthquake damage mitigation.Annu.Rev.Earth Planet.Sci.，2005，33：195－214

［11］Lee J，Friederich W，Meier T.Real time monitoring of moment magnitude by waveform inversion.Geophys.Res.Lett.，2012，39：L02309

［12］Guilhem A，Dreger D S.Rapid detection and characterization of large earthquakes using quasi－finitesource Green’s functions in continuous moment tensor inversion.Geophys.Res.Lett.，2011，38：L13318

［13］Tsuruoka H，Kawakatsu H，Urabe T.GRiD MT（grid－based real－time determination of moment tensors）monitoring the log－period seismic wavefield.Phys.Earth Planet.Inter.，2009，175：8－16

［14］Melgar D，Bock Y，Crowell B W.Real－time centroid moment tensor determination for large earthquakes from local and regional displacement records.Geophys.J.Int.，2012，188：703－718

［15］Crowell B W，Bock Y，Melgar D.Real－time inversion of GPS data for finite fault modeling and rapid hazard assessment.Geophys.Res.Lett.，2012，39：L09305

［16］Papazachos B C，Dimitriu P P.Tsunamis in and near Greece and their relation to the earthquake focal mechanisms.Natural Hazards，1991，4：161－170

［17］Ismoyo B.Indonesia battles disasters on two fronts.The Jakarta Globe 1.2010.http：∥thejakartaglobe.beritasatu.com／archive／indonesia－battles－disasters－ontwo－fronts／404050／

［18］Yue H，Lay T，Koper K D.En e′chelon and orthogonal fault ruptures of the 11April 2012great intraplate earthquakes.Nature，2012，490：245－249

［19］Bouchon M，Karabulut H，Aktar M，et al.Extended nucleation of the 1999 Mw 7.6Izmit earthquake.Science，2011，331：877－880

［20］Henzinger M.Search technologies for the Internet.Science，2007，317：468－471

［21］Bach J R，Fuller C，Gupta A，et al.Virage image search engine：an open framework for image management.SPIE，1996，2670：76－87

［22］Sahami M，Mittal V，Baluja S，et al.The happy searcher：challenges in web information retrieval.Proc.8th Pacific Rim Int.Conf.Artificial Intelligence，Springer，2004，3157：3－12

［23］Zhou W，Li H，Lu Y，et al.Large scale image retrieval with geometric coding.ACM International Conference on Multimedia（MM），2011：1349－1352

［24］Muja M，Lowe D G.Fast approximate nearest neighbors with automatic algorithm configuration.Proc.International Conf.Computer Vision Theory and Applications（VISAPP’09），2009，1：331

［25］Slaney M，Casey M.Locality－sensitive hashing for finding nearest neighbors.IEEE Signal Process.Mag.，2008，25：128－131

［26］Silpa－Anan C，Hartley R.Optimised KD－trees for fast image descriptor matching.Computer Vision and Pattern Recognition 1－8，Institute of Electrical and Electronics Engineers（IEEE），2008

［27］Wu P，Hoi S C H，Nguyen D D，et al.Randomly projected KD－trees with distance metric learning for image retrieval.Proc.17th Int.Conf.Adv.Multi.Model.Springer，2011：371－382

［28］Friedman J H，Bentley J L，Finkel R A.An algorithm for finding best matches in logarithmic expected time.ACM Trans.Math.Softw.，1977，3：209－226

［29］Berchtold S，Bhm C，Keim D A，et al.A cost model for nearest neighbor search in high－dimensional data space.Proc.16th ACM SIGACTSIGMOD－SIGART Symp.Principles of Database Systems，ACM Press，1997：78－86

［30］Yianilos P N.Data structure and algorithms for nearest neighbor search in general metric spaces.Proc.5th ACM－SIAM Symp.Discr.Algorithms，Society for Industrial and Applied Mathematics，1993：311－321

［31］Seidl T，Kriegel H P.Optimal multi－step k－nearest neighbor search.Proc.ACM SIGMOD Int.Conf.on Management of Data 27，SIGMOD，1998：154－165

［32］Arya S，Mount D M，Netanyahu N S，et al.Proc.of the Fifth Annual ACM－STAM Symp.on Discrete Algorithms.Association for Computing Machinery（ACM），1994：573－582

［33］Zhu L，Rivera L A.A note on the dynamic and static displacements from a point source in multilayered media.Geophys.J.Int.，2002，148：619－627

［34］Dziewonski A M，Anderson D L.Preliminary reference Earth model.Phys.Earth Planet Inter.，1981，25：297－356

［35］Ekstrom G，Nettles M.Global CMT Web Page.2014.http：∥www.globalcmt.org／

［36］National Earthquake Information Center—NEIC.2014.http：∥earthquake.usgs.gov／regional／neic／

［37］Shearer P M.Introduction to Seismology.Cambridge Univ.Press，1999

［38］Aguiar A C，Beroza G C.Page rank for earthquakes.Seismol.Res.Lett.，2014，85：344－350

［39］Jolliffe I T.Principal Component Analysis.Springer－Verlag，1986

学术论文

收稿日期：(＊)2015－01－26；采用日期：2015－07－10。

doi：10.3969／j.issn.0235－4975.2015.10.003

文献标识码：A；

中图分类号：P315.63；