LC元件级联电路模拟行波过程的有效性分析

李传健，陈炯聪，黄曙，郑文杰

（广东电网有限责任公司 电力科学研究院，广东 广州 510062）

高压远距离输电线路上行波的传输过程一般采用分布参数进行研究[1]，在分布参数电路中，考虑电磁量的空间分布特性，电压及电流不仅仅是时间的函数，而且还是距离的函数[2]，电压电流沿线路传输的过程称为波过程。

为了研究输电线上的波过程，传统方法是在具有分布参数特征的实际线路上进行试验，但是实际电力系统中的输电线路往往可以达到几百km甚至上千km，而且电力线路往往翻山越岭，穿插于各种复杂的地理环境，试验难度较大。为了便于研究线路上发生故障后的行波传输问题，目前亟需搭建一种可以近似模拟输电线上波过程的试验平台。

本文首先建立LC元件的级联模型并分析了利用该模型模拟分布参数线路波过程的基本原理，接着给出算例对该模拟方法的有效性进行证明，最后结合实际电力线路中行波的波过程，进一步分析了通过改变LC级联模型的分段数来逼近实际输电线模型的一般方法并进行了仿真验证。

1 LC元件级联模型模拟输电线波过程的基本原理

1.1 LC元件级联模型的建立

利用LC元件的级联形式模拟分布参数线路的一般思路是：电感和电容元件是集中参数元件，少量的LC元件级联时无法模拟相应的分布参数线路，但是如果用足够多的LC元件，通过级联形式连接在一起，就可以达到对分布参数线路上波过程的近似模拟效果。基于以上分析，将实际需要模拟的分布参数输电线路等分为n段，设线路的总电感为L，总电容为C，则n等分分成的每一小段线路可以用电感值为L/n，电容值为C/n的LC集中参数元件进行等效。由此建立LC元件级联模型如图1所示。

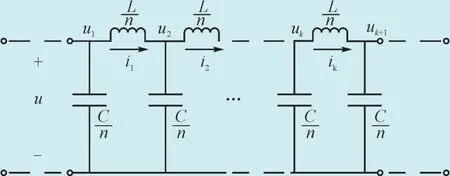
图1 LC元件级联模拟输电线波过程模型Fig. 1 Model of the wave process simulation by using LC element cascade circuit

模型中仅采用电感和电容元件对实际输电线路进行模拟，当采用的LC元件的个数逐渐增加时，理论上模拟的精度也会相应增加，当元件的个数趋于无穷时将近似等效于分布参数表示的输电线路。

1.2 迭代方程的推导

在如图1所示的LC元件级联模型中，取电感元件两端的节点电压和流过电感元件的电流作为求解变量[4]，可以得到该模型下的电压电流关系方程如下：

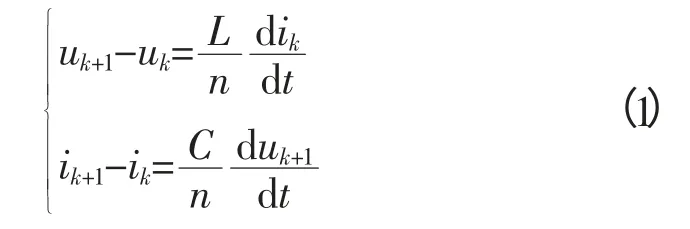
接着对该方程组中的电压以及电流对时间的导数项进行差分化处理，即对求解的时间进行离散化，设求解总时间为T，按步长为Δt对其进行离散，电压及电流交替设置，共离散为M段，初始时刻为0，时间离散后依次为Δt，2Δt，…，MΔt。经过交替离散后模型中一点处的电压电流迭代关系如图2所示。

图2 LC元件级联模型的时间离散示意图Fig. 2 Discrete-time model of the LC element cascade circuit

按照以上过程，LC元件级联模型中的电压和电流就变成了一组时间上的离散点。经过以上处理后可得如下方程：

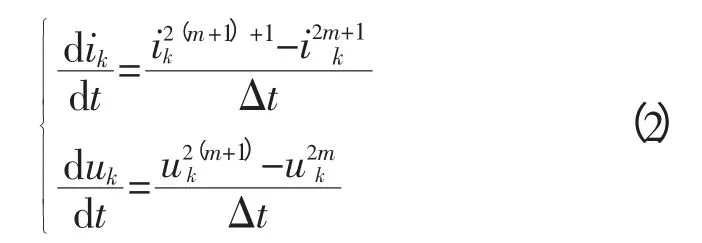
将式（2）代入式（1）中，可以得到差分化之后的电压电流关系方程如下：

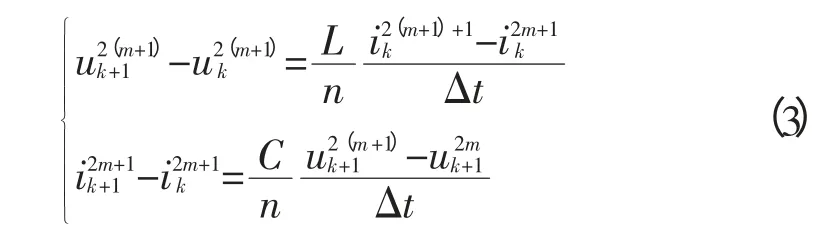
进一步整理可得电压及电流的迭代方程为：

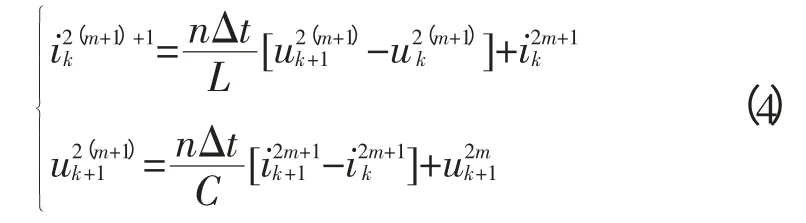
式（4）即为LC元件级联模型的电压及电流迭代方程。

1.3 LC级联模型下迭代方程的求解

已经得到了电压及电流的迭代方程，结合具体的边界条件就可以对LC级联模型中的电压及电流进行求解。考虑待模拟输电线路末端开路，输电线总电感及总电容值已知，按照1.1节所述对输电线建立LC元件级联模型如图3所示。

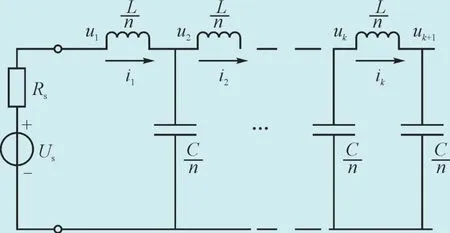
图3 LC元件级联模拟实际输电线末端开路模型Fig. 3 Model of the LC element cascade circuit with the ends of the line open

设输电线始端有一理想电压源Us，Rs为输电线始端负载。整条输电线等分为n个由LC元件级联构成的集中参数区段，每个区段的电感值为L/n，对地电容值为C/n。线路始端和末端均满足基尔霍夫定律[5]，由此即可以推导出该模型下始端及终端的边界条件。

如图3所示，线路始端的电压电流满足如下关系：

对应的迭代方程为：

式（6）即为线路始端的边界条件对应的迭代方程；

线路末端的电压及电流满足如下关系：

对式（7）等号右边进行差分化，即代入：

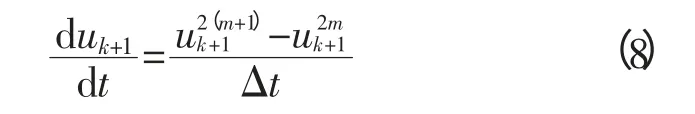
整理可得线路末端边界条件对应的迭代方程为：

综上，结合式（4），式（6）以及式（9）得到了LC级联模型对应的迭代方程组，即可对模型中的电压及电流进行求解。

2 LC级联模型的算例验证

为了验证基于LC元件级联模型的迭代算法的正确性，选取一定参数的电感及电容元件搭建级联实物模型，通过比较利用示波器读取的模型中的电压波形和利用迭代算法程序计算得到的各点电压进行描点作图所得到的波形来进行分析验证。

在本算例中选取0.15 mH的电感及0.01 μF的电容器各7个，搭建LC级联模型如图4所示。

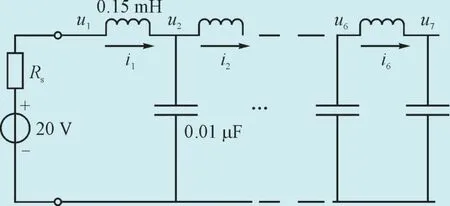
图4 LC元件级联算例验证电路Fig. 4 Calculation examples of the LC element cascade circuit

由前面介绍的迭代算法原理可以得到对应于该模型下的电压电流迭代方程以及线路始端与末端的边界条件如下。

迭代方程：

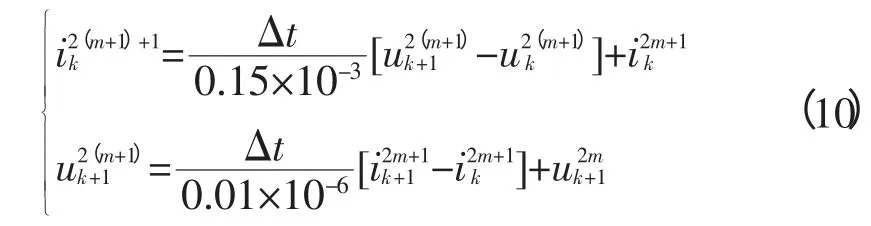
线路始端及末端的边界条件：

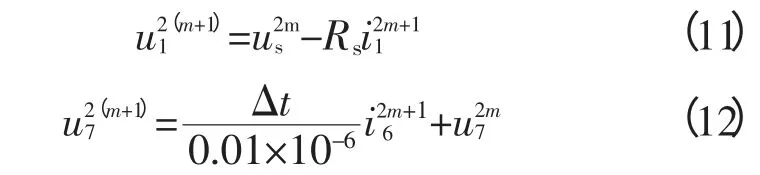
由式（10）～式（12）可以计算得到对应时刻模型中各点电压及电流的幅值。将线路始端节点电压和线路末端节点电压的迭代计算值取出，并在Matlab中绘制成图线。在电压波形突变位置局部放大可以得到如图5所示波形。

图5中虚线为线路始端电压波形，实线为线路末端电压波形。在实际模型中由示波器读取的波形数据取出后在Matlab中绘图可以得到实测电压在波头位置处的波形如图6所示。

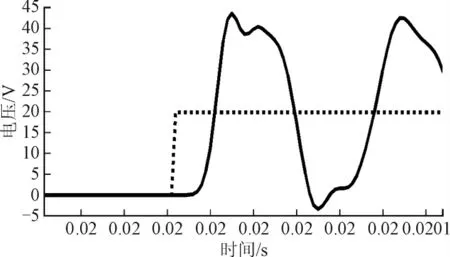
图5 迭代算法计算得到的电压局部波形Fig. 5 Partial voltage waveform calculated by iterative algorithm

图6 LC级联模型中实测得到的电压波形Fig. 6 Measured voltage waveform of the LC element cascade circuit

图6中虚线为线路始端电压波形，实线为线路末端电压波形。对比图5和图6，可见由迭代算法程序得到的电压波形和实测电压波形基本一致，由此验证了基于LC级联模型的电压迭代算法的正确性。

3 LC级联模型与分布参数模型的对比分析

3.1 两个模型的对比

实际电力线路的均匀输电线分布参数模型如图7所示。

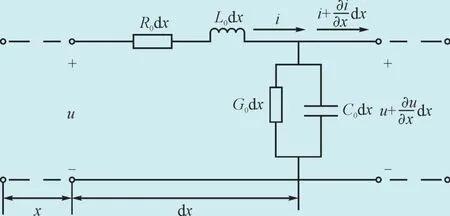
图7 均匀输电线的分布参数模型Fig. 7 Distributed parameter model of uniform transmission line

由图7，应用电路理论可以推导得到该输电线分布参数模型的微分方程为：

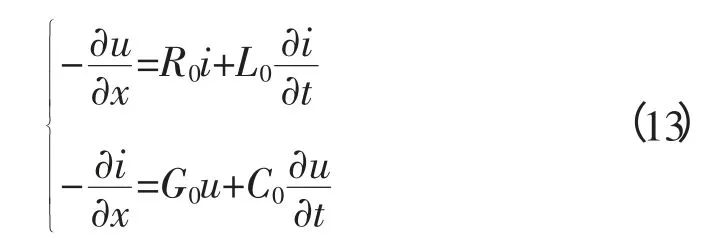
而对于均匀无损输电线，不考虑导线的电阻和漏电导，即R0、G0为零的情况下，式（13）可以化为一阶波动方程：

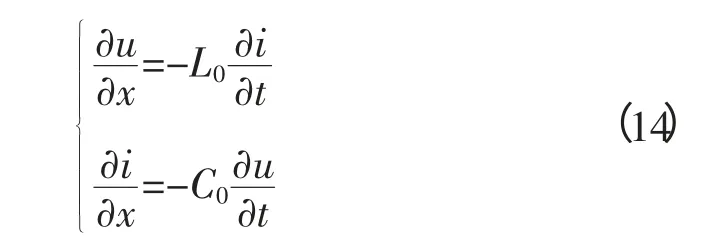
对比于式（14），LC元件级联模型的的迭代方程为一组离散化的电压电流关系方程，重列如式（15）所示。

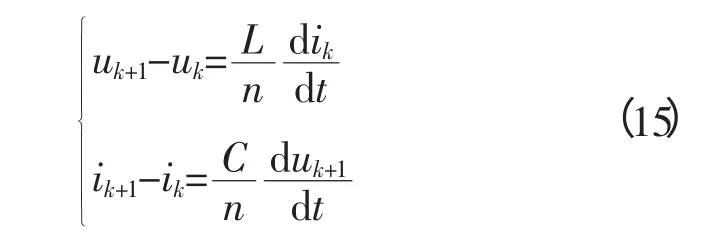
这里需要指出：当LC级联模型中的分段数n不断增大时，式（14）和式（15）中方程的解将越来越接近；极限情况下，当n趋于无穷时，实际线路的分布参数模型所对应的波动方程和基于LC元件级联模型下的电压电流迭代方程将统一起来，其实际意义在于具有无穷分段的级联模型将等效模拟实际分布参数线路上的波过程。

3.2 LC级联模型下的T-n关系研究

由前述分析已经知道级联模型中的分段数n越多，则模型对实际线路上行波波过程的模拟效果越好，下面首先应用ATP软件对实际分布参数线路的波过程进行仿真，通过仿真得到分布参数模型中电压行波到达线路末端的时间理论值并以此为衡量LC级联模型模拟分布参数线路波过程的指标，接着对不断增加分段数n的LC元件级联模型进行电压电流的迭代计算，定量分析模型中的分段数n与行波到达线路末端的时间T之间的关系。

在对实际分布参数线路进行仿真时选取5 km架空线建立仿真模型，模型中架空线路单位长度的电感及电容值均根据工程实际中的参数值在ATP中进行设定，单位长度的电感值为L1=1.273×10－3H/km，实际架空线路单位长度的电容值为C1=0.009 07 μF/km，架空线总电感为：L=5×L1=6.366 mH，架空线总电容值为：C=5×C1=0.045 35 μF。线路始端接有工频电压源，开关闭合后，线路上将产生一电压行波从线路始端向末端传播，分别在始端和末端节点处设置电压探针监测电压行波。

首先由架空线路单位长度的电感电容值可以计算出线路上电压行波的传输速度理论值为：

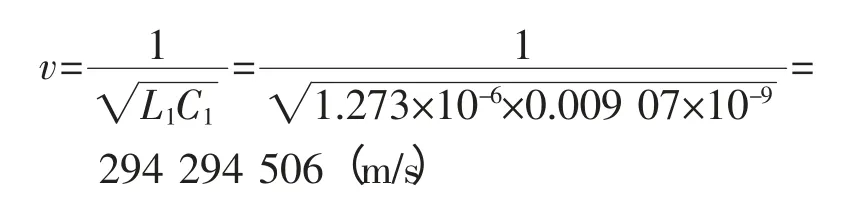
则行波到达始端及末端的时间差理论上也可以计算得到：

对模型进行仿真得到线路始端节点和线路末端节点检测到的电压行波波头部分局部放大如图8所示。

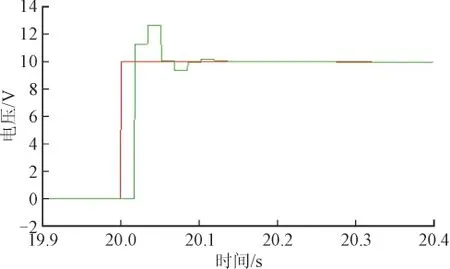
图8 线路始端及末端行波波头局部放大图Fig. 8 Traveling wave head at the beginning and the end of line

图8中红色曲线为线路始端电压波形；绿色曲线为线路末端电压波形。由图8可得：行波波头到达线路末端和始端的时间差为T=1.7×10－5s，与理论计算所得结果相同，证明所建立的仿真模型可以达到模拟实际5 km线路的要求。

按照迭代计算的步骤分别对5分段和20分段的LC级联模型中的电压进行迭代求解，而后将模型中的始端节点电压和末端节点电压的迭代计算值取出，在Matlab中绘制成图线并在电压波形突变位置局部放大可以得到对应分段数的波形，最后通过波形确定该n值下的时间T，与5 km分布参数线路给出的时间理论值进行比较。

1）5分段LC级联模型波过程的波形如图9所示。

图9中绿色曲线为线路始端电压波形；红色曲线为线路末端电压波形。由波形可以得到n=5 时，对应的电压到达始端及末端的时间差为：

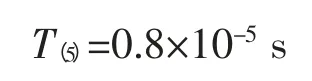
2）20分段LC级联模型波过程的波形如图10所示。

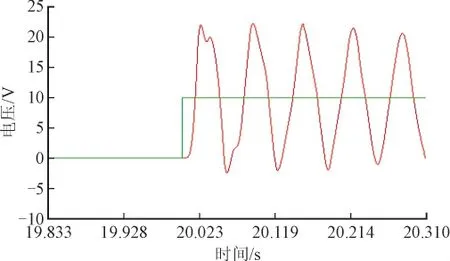
图9 5分段LC级联模型的电压波形Fig. 9 Voltage waveform of the 5-section LC element cascade circuit

图10 20分段LC级联模型的电压波形Fig. 10 Voltage waveform of the twenty-section LC element cascade circuit

图10中绿色曲线为线路始端电压波形；红色曲线为线路末端电压波形。由波形可以得到n=20时，对应的电压到达始端及末端的时间差为：

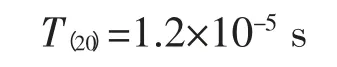
3）LC级联模型中的T-n关系

在上述分析的基础上不断增加分段数n，并通过补充实验仿真数据来对T-n关系进行较为精确地分析：这里选取n=5，10，20，50，100，对每一个n值下的LC级联模型按照迭代方程进行计算并通过绘制的电压波形得出波头到达始端及末端节点的时间差，将不同的分段数n、对应于分段数的区段LC参数值以及最终得到的电压到达线路始端及末端的时间差列表1如下。

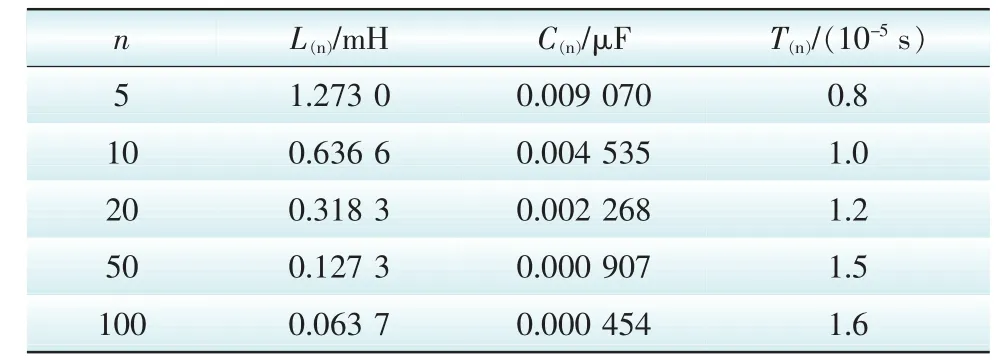
表1 LC模型优化数据表Tab. 1 Data of LC element cascade circuit with different partition numbers

将表1中的数据在matlab中应用三次样条插值绘制成T-n关系曲线，如图11所示。

图11 LC级联模型及实际线路行波的T-n关系图Fig. 11 T-n relationship between LC element cascade circuit and the actual line

在该图中，曲线为不断增加分段数n的LC级联模型的T-n曲线，线上’*’标注的点为实验得出的数据点，图中T=1.7×10－5s所代表的直线为实际5 km分布参数线路电压行波到达始端及末端的时间差。

由上图曲线可以得出结论：随着n值的不断增加，LC级联模型对实际分布参数线路的波过程模拟将越来越精确，具体体现在LC级联模型中波头到达线路末端的时间越来越接近实际线路行波传输的真实值。

下面以10分段LC级联模型为例，分别模拟5，10，15，20 km的实际架空线路，即通过迭代算法得到模型中电压信号到达始端及末端的时间差，参考实际架空线路行波的波速得到10分段模型可以用来模拟的实际线路长度。

以5 km线路为例，由表1已经得到n=10的LC级联模型所对应的电压传输时间为T=1.0×10－5s，则该模型可以模拟的实际架空线路长度为：

s=vT=294 294 506×1.0×10－5=2 942.95（km）

将待模拟的实际线路长度、10分段级联模型中对应各长度的单位电感电容值以及最后得到的实际可模拟线路长度（SLC）绘制成表2如下。

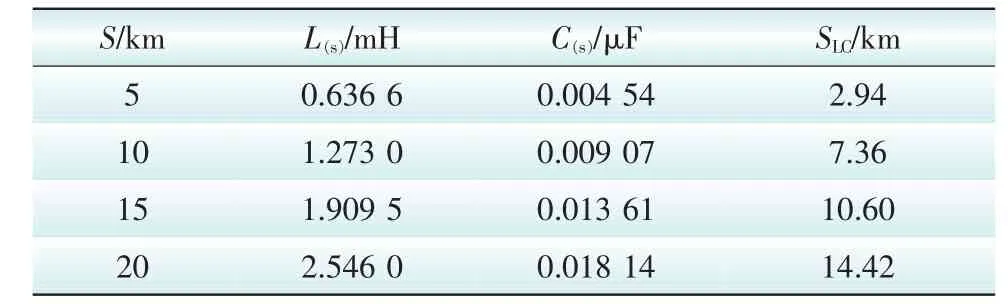
表2 10分段模型模拟实际线路长度表Tab.2 The simulation of the actual length of transmission line by ten-section LC element cascade circuit

由表2可以得到n=10时的LC元件级联模型模拟不同长度实际架空线路所得到的等效模拟长度，对应于不同的分段数n同样可以得到实际线路的对应模拟长度，由此即得到了利用集中参数元件模拟分布参数线路的定量关系，为利用LC元件搭建实际线路模型进行波过程的相关分析提供了理论依据。

4 结语

本文介绍了一种利用LC元件级联模型对输电线波过程进行模拟的方法，对LC级联模型进行了较为详细的分析，推导出了基于该模型的电压电流迭代方程并通过算例验证了该迭代方法的准确性。最后建立模型对实际线路的波过程进行仿真模拟，并通过迭代方程对不同n值下的模型中的电压进行计算，得到的T-n关系表明，不断增加LC元件的个数来改进级联模型可以达到模拟实际线路波过程的良好效果。

[1] 张希，刘宗行，孙韬. 传输线方程的一种数值解法[J]. 重庆大学学报: 自然科学版，2004，27（2）: 116-119.ZHANG Xi，LIU Zonghang，SUN Tao.A numerical method for transmission line equations[J]. Journal of Chongqing University，2004，27（2）: 116-119（in Chinese）.

[2] 黄伟，庞琳，曹彬，等. 基于分区解耦的配电网状态估计的分布式并行计算[J]. 电力系统保护与控制，2014，（15）: 45-51.HUANG Wei，PANG Lin，CAO Bin，et al. Parallel and distributed computing for an area-decoupled state estimation method for distribution systems[J]. Power System Protection and Control，2014（15）: 45-51（in Chinese）.

[3] 韩昆仑，蔡泽祥，贺智，等. 高压直流输电线路故障行波传播特性及其对行波保护的影响[J]. 电力系统保护与控制，2013（21）: 20-25.HAN Kunlun，CAI Zexiang，HE Zhi，et al. Propagation characteristic of fault traveling wave on HVDC line and its influence on HVDC line traveling wave protection[J].Power System Protection and Control，2013，（21）: 20-25（in Chinese）.

[4] 谢志远，王岩，郭以贺，等. 传输线电气参数测试方法研究与应用[J]. 电力系统保护与控制，2012（40）: 151-155. DOI:10.3969/j.issn.1674-3415.2012.08.028.XIE Zhiyuan，WANG Yan，GUO Yihe，et al. Research and application of testing method for electrical parameters of transmission lines[J]. Power System Protection and Control，2012（40）: 151-155. DOI:10.3969/j.issn.1674-3415.2012.08.028（in Chinese）.

[5] PAUL C R. Incorporation of terminal constraints in the FDTD analysis of transmission lines[J]. IEEE Transactions on Electromagnetic Compatibility，1994，36（2）: 85-91.

[6] 董霞，刘志珍，宁大海，等. 基于传输线模型的三相变压器直流偏磁仿真分析[J]. 电力系统保护与控制，2012（23）: 12-16.DONG Xia，LIU Zhizhen，NING Dahai，et al. Simulation study for the three-phase transformer under DC bias based on the transmission-line model[J]. Power System Protection and Control，2012（23）: 12-16（in Chinese）.

[7] DE PáDUA MOREIRA R，DE MENEZES L R A X.Direct synthesis of microwave filters using inverse scattering transmission-line matrix method[J]. IEEE Transactions on Microwave Theory and Techniques，2000，48（12）:2271-2276.

[8] 王晖，谢树果，宁敏. 传输线矩阵法细线模型的馈电方法[J]. 遥测遥控，2010，31（2）.WANG Hui，XIE Shuguo，NING Min. A feed method for thin-wire model of transm ission-line matrix[J]. Journal of Telemetry，Tracking and Command，2010，31（2）（in Chinese）.

[9] MAO J F，LI Z F. Analysis of the time response of nonuniform multiconductor transmission lines with a method of equivalent cascaded network Chain[J]. IEEE Transactions on Microwave Theory and Techniques，1992，40（5）: 948-954.

[10] 高方平，姚缨英，季苏蕾. 用FDTD法求解传输线方程[J].华北电力大学学报，2012，39（2）: 12-16.GAO Fangping，YAO Yingying，JI Sulei. Using the finitedifference time-domain（FDTD）method to solve transmission-line equations[J]. Journal of North China Electric Power University，2012，39（2）: 12-16（in Chinese）.

[11] 靳晋忠，刘强，姚恺. 对均匀传输线分布参数电路的讨论[J]. 河南职技师院学报，2000（3）：54-55.JIN Jinzhong，LIU Qiang，YAO Kai. On the distributing parameter circuit in well-transmission line[J]. Journal of Henan Vocation-Technical Teachers College，2000（3）：54-55（in Chinese）.

[12] 和伟，高修纲. 高频传输线方程适用性的讨论[J]. 电波科学学报，2000，15（3）: 275-277.HE Wei，HAO Jianming，GAO Yougang. Discussion of transmission line equations at high frequency[J]. Chinese Journal of Radio Science，2000，15（3）: 275-277（in Chinese）.

[13] TAYLOR C，SATTERWHITE R，HARRISON C，Jr. The response of a terminated two-wire transmission line excited by a nonuniform electromagnetic field[J]. IEEE Transactions on Antennas and Propagation，1965，13（6）: 987-989.

[14] NAMIKI T. A new FDTD algorithm based on alternatingdirection implicit method[J]. IEEE Transactions on，Microwave Theory and Techniques，1999，47（10）: 2003-2007.

[15] KELLEY D F，LUEBBERS R J. Piecewise linear recursive convolution for dispersive media using FDTD[J]. IEEE Transactions on Antennas and Propagation，1996，44（6）:792-797.

[16] MELLOR P H，ROBERTS D，TURNER D R. Lumped parameter thermal model for electrical machines of TEFC design[C]// IEE Proceedings B （Electric Power Applications）. IEE，1991，138（5）: 205-218.

[17] ZHU Z Q，PANG Y，HOWE D，et al. Analysis of electromagnetic performance of flux-switching permanentmagnet machines by nonlinear adaptive lumped parameter magnetic circuit model[J]. IEEE Transactions on Magnetics，2005，41（11）: 4277-4287.

[18] GOLDFARB M，CELANOVIC N. A lumped parameter electromechanical model for describing the nonlinear behavior of piezoelectric actuators[J]. Journal of Dynamic Systems，Measurement，and Control，1997，119（3）: 478-485.

[19] AHMED N U，TEO K L. Optimal control of distributed parameter systems[M]. Elsevier Science Inc.，1981.

[20] 刘红，张东来. 电力线载波中传输线模型的建立及应用[J]. 电力系统及其自动化学报，2002，14（3）: 27-31.LIU Hong，ZHANG Donglai. The establishment and application of transmission line model in power line carrier[J]. Proceedings of the EPSA，2002，14（3）: 27-31（in Chinese）.