一种弹性评估模型

尹金娣

(西安电子科技大学数学与统计学院，陕西西安 710071)

随着信息技术的不断发展，网络安全和可靠性普遍得到人们的重视。人们花费大量的财力物力对网络风险、网络可靠性等方面进行研究使其系统的服务质量得到提高。但当前的网络面对突如其来的灾难和人为攻击显得十分脆弱［1－2］。从而使网络弹性的研究成为了一个研究热点。网络弹性的研究不再局限于被动对网络遭到攻击失效后的评估，而是主动的进行对故障提前预测同时及时恢复失效信息。本文主要对网络弹性概念的梳理、网络弹性评估和度量所面临的挑战进行分析与探讨，且最为重要的是提出了新的系统弹性评估方法。该种模型基于马尔科夫网络，不但考虑了单个服务的状态，同时融入了服务之间的依赖关系，更准确地评估整个系统的弹性。

1 弹性度量模型

以前改进系统弹性的工作主要是关于考虑威胁影响基础上的，其中包括对设计、构架、绩效的评估。弹性系统的设计提出是为了检测和修复各种类型的故障，被应用到弹性方面的模型绝大多数是基于可靠性的。Nicol［3］提出一种基于模型的评估调查技术来量化可靠性和安全性诸多模型。此外，还可应用到系统的弹性领域。然而，故障的解决是通过模型清楚地定义和统计预测。相比在恶意攻击的系统中，失效率的预测更加困难。文中考虑了无法统计推断的故障，如恶意攻击绝大多数的工作涉及对恶意攻击的探测和预防，而不仅是关注这种威胁的后果。

1.1 弹性度量模框架

弹性是理解为系统的适应能力。该模型的弹性定义如下:弹性是一种重要服务的适应能力，以及系统应对突发事件的能力。量化弹性模型考虑单个服务的适应能力以及其之间的相互依赖关系。衡量服务的适应性，文中使用了自适应性指标，其主要包括高、中、低3个状态。其是计算单个服务的状态，然后聚合作为一个联合概率分布，用于计算整个系统的弹性。系统的所有服务状态的联合概率分布被定义为弹性函数R。该函数，在式(1)中呈现。计算重要服务Sc的概率并未在低的适应状态，而其他非重要服务Snc则处于低状态

为简洁有效地表示和计算联合分布，该模型应用了马尔科夫网络表现形式［4］。马尔科夫网络基于无向图，其节点表示变量，边表示节点之间的链接。然而，对于马尔科夫网络，联合分布是由因子组成的，而不是节点。一个因子特征函数φ(x)被定义为φ(x):x→R+;且一个因子通常包含由多个节点组成的图，而马尔科夫网络则被定义成最大因子的集合图。给定一系列变量 X{x1，x2，x3，…，xn}，一个马尔科夫网络被定义为

其中，F是图中变所属因子的变量集合，Z为常量，通常使其单位化。文献［4～5］在马尔科夫网络上作了详细论述。本文提到的弹性量化模型包含H，S，T和F。H表示系统在评价下的服务图;S表示部分系统服务集，其中服务的种类分为重要服务Sc和非重要服务Snc;T表示服务状态模型，服务可能有较多不同的状态;状态模型定义了服务的状态种类，同时定义了如何度量服务状态的指标;F表示因子，因子能刻画服务图，同时推算出系统弹性。

1.2 度量元素

服务图H能呈现系统中的服务彼此如何链接。一个服务图H(S，L)为一个无向图，一系列服务用点S={S1，S2，…，Sn}来表示，链接用边 L={l1，l2，…，ln}来表示。边的存在有且仅当两个服务之间至少有一个交易。一个交易被定义如下:给定两个服务X和Y，若在X和Y之间有一个信息交换的行为，无论成功或失败，则称T(X，Y)为一个交易。服务图是通过分析服务之间的网络交易而建立的。为防止两个服务之间无访问信息交换，文中在预期交易的基础上创建交易。

对于服务S，一个系统的弹性如前所述，通过服务来量化。本文使用服务定义为:服务是为系统中其他项目提供一种功能的软件。服务有多种描述不同水平的操作级别状态。例如，失常、一般、可接受、不可接受等。重要服务Sc对系统的正常运行是较重要的，其通常优先于其他服务。对于重要服务的识别，研究与从业人员采取了不同的方法［6－7］，通常可利用重要服务系统专家进行识别［8］。

服务状态模型T:量化系统弹性，文中主要考虑个体服务的状态和其之间的相互依赖关系。状态模型定义了高、中、低3种自适应状态。较低的自适应服务意味着其不能正确地响应环境变化，较高的自适应服务则变现相反，目前自适应指标已被广泛应用［9］。在文中，提出了不同于以往的自适应指标。本文自适应指标是基于服务性能属性，评估自适应可能有一个或多个属性决定。为计算服务的自适应，首先要评估服务的性能属性。属性通常说明服务需监控的重要方面，用 Pa={pa1，pa2，…，pan}表示一组属性，其中 pai表示一个属性。此外，还设置了一组参数 W={w1，w2，…，wn}，用于表示属性之间相关联的权重。自适应的度量基于单个服务的评估分数。因此，性能属性必须聚合到最后得分。在创建汇总得分方面，使属性值规范化，然后加权计算生成最终得分

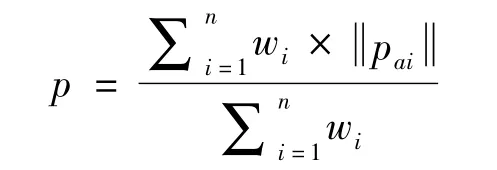
假设一个服务有3个性Pa={2.1，0.8，3.4}能属性，权重W={2，1，1}，性能得分计算如下:首先使Pa规范化，然后结合相应的权重，计算出 P=(0.62×2+0.23×1+1×1)/3→0.823。同时，每个属性值定期计算，从而推算出一组性能得分P={p1，p2，…，pn}，最终解决单个服务的自适应状态度量。在计算单个服务自适应状态之前，必须计算自适应得分，其是介于性能得分与服务自适应之间的。文中假设ai代表在i数据点的自适应得分，pi－1和pi分别代表在数据点i－1和i的性能得分。自适应得分ai是由 pi－1和 pi根据式(2)计算得出。例如，pi=0.6 和0.60→0.54。通过此种方法计算出一组单个服务的自适应得分 A={a1，a2，…，an－1}。

然后根据A设置一个单个服务的自适应状态的阈值，阈值可自动或手动生成。本文的阈值由系统自动生成。评价单个服务自适应状态的方程为

其中，t1和t2为自适应状态的两个阈值。

F因子代表服务图中最大的集团结构，其在马尔科夫网络中呈现出条件概率分布。例如，在服务图1中，有4个服务{A，B，C，D}，有3个最大集团{A －B，C－B，D－B}。因此，有3个相关的条件概率分布因子，用其来计算出特定系统的联合概率分布。

图1 结构图

1.3 建立弹性量化模型的步骤

建立弹性量化模型分为6个步骤，从数据的采集到弹性的量化和推理。

步骤1 重要服务的分配:这是一个通过系统专家手动的过程。

步骤2 数据采集:包括在服务主机获取数据和在中央存储器处理数据。且每个服务生成一组数据，包括其与其他服务交易的信息以及自身性能属性测量。

步骤3 自适应计算:这一过程的计算遵循服务状态模型T从所在服务获取性能属性值，从而推算出自适应得分，进而得到自适应状态，该状态的评估是根据式(3)进行，得到结果后利用马尔科夫网络计算出其条件概率分布。

步骤4 服务图:此图是基于服务之间的交易而建立的。在系统中，每个时间段一个服务与另一个服务进行交流，其中两者之间的交易被创建和存储。这些信息检索过后生成服务图，在服务图中，两个服务之间的链接表示其间的交易。

步骤5 计算条件概率分布:首先要确定服务图中的因子。如上文所述，因子是根据服务所在关系的最大集团得到的。一旦集团确立，基于自适应状态的条件概率分布也会被计算出。

步骤6 弹性度量:模型一旦确立，可查询重要服务，计算条件概率分布，并最终根据式(1)计算出相应的系统弹性。

为便于理解，举例进行说明，如图1所示。该系统包括4个服务{A、B、C、D}，其中B服务是重要服务，其连接着其他3个服务。该服务图中有3个最大集团{A－B、C－B、D－B}。假设系统中的服务状态模型只有两种状态t和f。由于B是重要服务，必须保持在t状态，系统才能正常运行。弹性方程根据式(1)演化生成

然后，随机取值用于表示因子特征函数的值φ(A，B)={30，5，1，10}，φ(C，B)={100，1，1，100}，φ(D，B)={1，100，100，1}。其中，每个值代表对应服务组的状态。例如bf=30，afbt=5，依次类推。这些值被用于计算每个因子的条件概率分布。利用上述弹性方程，可计算出R=(5×1×100)/［(30×100×1)+(5×1×100)］→500/3 500≈0.14。

2 弹性评估模型实际应用

为评估该模型，将计算SCADA系统［10］，其控制重要的基础设施，如电网、核电站等。在一个典型的SCADA部署中，MTUs(Master Terminal Units)负责管理领域节点。HMI(Human－Machine Interaction)服务器对允许操作者的指令负责，同时与领域设备相互作用。RTUs(Remote Terminal Units)和PLCs(Programmable Logic Controllers)均是控制和监测输电线路的设备。Historians是用来收集发生在系统中的操作日志;Relational Databases用于存储被HMI和MTUs使用的信息。

为更好地理解SCADA系统与其服务功能，下面使用以下术语:css01(controller service server 01)，cdb01(central database server 01)，chs01(central HMI server 01)以及crs01(central remote servers)。有3个领域网络 f00，f01和 f02。r01代表 RTU01，sr01代表 sensor 01，p01代表PLC01。因存在PLCs、RTUs和sensors属于不同领域网络，服务名称被定义为领域网络代码和服务代码的组合。例如f01r01表示URTr01与领域网络f01的组合。在图2中，服务图表示系统包括43个节点，为避免逐一说明，文中使用XX表示列举的两位数相同类型的服务。系统中有3个MTUs(cssXX)，一个central historian(ch01)，一个 relational database(cdb01)，一个 HMI server(chsXX)，两个被用来为远程用户提供访问的remote servers(crsXX)以及多路RTUs(fXXrXX)，sensors(fXXsrXX)，PLCs(fXXpXX)。

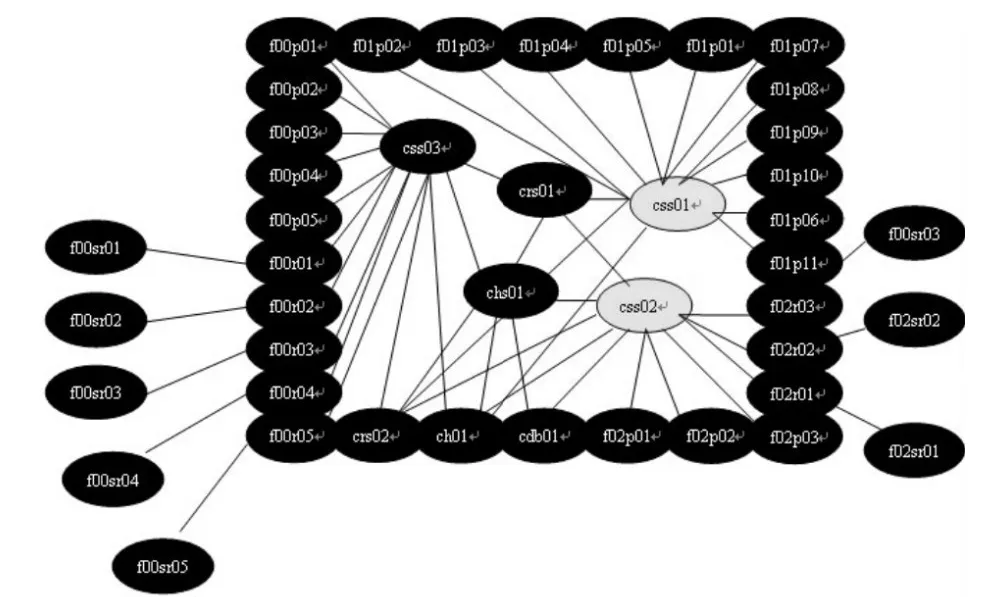
图2 SCADA系统

SCADA的仿真基于排队理论模型，每个服务代表一个队列，且服务时间符合指数分布，领域服务队列大小受限，而HMI，historian和remote servers均定义成队列大小不受限制。文中定义了css01和css02两个重要服务。因此，其他服务为非重要服务。根据式(1)，弹性方程可表示为

在仿真阶段，需要检测真实的服务时间(AST)属性。其包括服务时间和排队时间，并记录每次的请求处理。在一个服务是另一个服务的客户端情况下，AST是接受提供服务者响应的总时间，自适应指标通过计算这些属性而得到。服务图在图2中呈现，其中包括45个最大集团。因此，45个因子被用于计算弹性方程。

表1 重要服务所在的非重要服务处在高状态水平

表2 重要服务所在的非重要服务处在中间状态水平

表3 重要服务所在的非重要服务处在低状态水平

通过文献［10］，仿真在系统运行一天的基础上进行，其一共运行10次，一个平均AST可被用到。其中，状态阈值为t1=0.35和t2=0.70。用式(5)计算系统弹性，因css01和css02是独立的，根据已有的非重要服务，计算表达式0.005)≈0.28。该结果显示系统处在一个较低的弹性状水平，主要是因css01处在低水平自适应状态的概率较大。在表3中，可看到P(css01=low)≈0.72。

同样可用该模型去发现系统的其他方面。例如，在表1和表2中，改变非重要服务的自适应状态，可得到一个有价值的结果。当非重要服务设置为一个高自适应状态水平时，在表1中可看到系统弹性从R=0.28降至R=0.20。该结果显示，对于当前数据即使非重要服务的自适应能力提高，也未必有助于提高系统的弹性。进一步说，这是由于css01处在低状态有着较高的概率P(css02=low)≈0.11;另一个方面，css02也响应改变。因此，可通过表1和表2观察相关变化。在表2中，改变非重要服务状态水平，从高到中，使得css01和css02处在低状态水平是一个高概率事件。其中，P(css01=low)≈0.96，P(css02=low)≈0.11。由此可发现，css01受到影响最大，故 css01主要负责系统弹性。

3 结束语

弹性研究是网络和社会工程研究的热点与难点问题，而研究其特点和性质需尽量结合特定的领域去分析。通过建立合理的模型对弹性进行评估与量化，对预测和决策有较大帮助。学者和研究部门提出量化弹性的相应指标，是建立评估模型的关键。本文主要通过设定一些服务属性指标，计算出相应的性能得分，在一组性能得分基础上推出单个服务的自适应得分和服务状态。并结合马尔科夫网络模型及弹性函数方程，评估整个网络的弹性。本文不仅考虑了单个服务的状态，且结合了服务之间的相互依赖关系。在日后的网络弹性度量方面，对状态阈值的设定和故障的快速查找将是下一步需要深入研究的重点。

［1］ 刘密霞.网络弹性研究进展［J］.计算机科学，2013，11(40):46－49.

［2］于海生.协调与弹性［M］.北京:科学出版社，2012.

［3］Nicol D M，Sanders WH，Trivedi K S.Model－ based evaluation:from dependability to security［J］.IEEE Transactions on Dependable and Secure Computing，2004，1(1):48 －65.

［4］Kinderman R，Snell K.Markov random fields and their applications［M］.Providence，RI，USA:American Mathematical Society，1980.

［5］Koller D，Friedman N.Probabilistic graphical models principles and techniques［M］.Cambridge，MA，USA:MIT Press，2009.

［6］Wasserman S，Faust K.Social network analysis:methods and applications［M］.Cambridge，UK:Cambridge University Press，1994.

［7］Borgatti S.Identifying sets of key players in a socialnetwork，Comput［J］.Mathematic Organization Theory，2006，12(1):21－34.

［8］Heegaard P，Trivedi K B.Survivability quantification of communication services［C］.Anchorage，AK，USA:In Proceeding of 38th IEEE Interaction Conference DSN，2008:462 －471.

［9］Reinecke P，Wolter K.BAdaptivity metric and performance for restart strategies in web services reliable messaging［C］.New York，NY，USA:In Proc.7th Interaction Workshop Software Perform，2008:201 －212.

［10］Weiss J.Protecting industrial control systems from electronic threats［M］.New York，NY，USA:Momentum Press，2010.