一种快速高效的人工蜂群算法

王晓娟

(西安电子科技大学数学与统计学院，陕西西安 710071)

近年来，人工蜂群算法［1］由于其良好的搜索能力和强大的实际应用背景，得到了快速的发展，人工蜂群算法的改进体也相继而出。但该算法仍面临着诸多难题。随着越来越多的研究，其收敛速度慢，在解决高维多峰问题时易陷入局部最优等缺点给学者带来了困难和挑战。在文献［2］中作者用排序选择代替了贪婪选择，维持种群的多样性，又加入了随机动态搜索算子用来进行局部搜索，加快了算法的收敛速度;在文献［3］中，由于人工蜂群算法的变异方程存在着全局搜索能力强而局部搜索能力弱的缺陷，受改进的差分进化算法的影响，提出了一种新的变异方程，该变异方程在最优解附近进行搜索，提高了算法的局部搜索能力;文献［4］提出了基于ABC改进的优秀种群引导的人工蜂群算法(Gbest－guided Artificial Bee Colony Algorithm，GABC)等。基于单维搜索的雇佣蜂由于改变量小，而使得ABC算法收敛速度较慢;本文借鉴了回溯搜索优化算法(Backtracking Search Optimization Algorithm，BSA)［5］的搜索方式，BSA在变异扰动方程中，基向量无旋转，这与ABC的变异方式相似。故本文结合蜂群算法的特点，使BSA的搜索方式与雇佣蜂结合，得到了一种基于多维和一维混合搜索策略的改进雇佣蜂，使得搜索策略更加快速高效，并改进了跟随蜂的蜜源选择策略，增加了种群多样性。

1 人工蜂群算法

人工蜂群算法可分为4部分:初始化食物源、雇佣蜂开采、跟随蜂开采和观察蜂替换食物源。初始化食物源方式为

食物源表示问题的可行解，xi，j表示第i个食物源xi的第 j维元素，其中 i=1，2，…，ps，j=1，2，…，D，D 为问题的维数，ps为种群规模，［aj，bj］表示问题第 j维元素的区间。随机生成ps个食物源后，交给雇佣蜂进行开采，开采方程如下

vi，j是变异后第i个个体vi的第j维元素，vi是雇佣蜂随机选取一个不同于xi的食物源，j是随机选择的一个位置索引，r是［－1，1］之间的一个随机数。当产生新的食物源后，雇佣蜂会根据食物源的适应度值，并在vi和xi之间作贪心法选择。第i个个体适应度值fitnessi的计算公式为

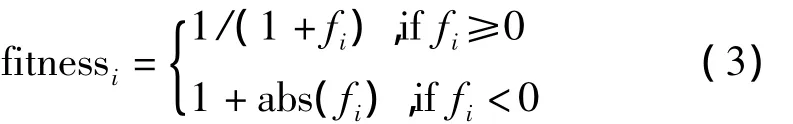
雇佣蜂开采完后交给跟随蜂开采，跟随蜂不同于雇佣蜂，其会选择性开采食物源，每个食物源的被选择概率probi计算公式为

跟随蜂先根据轮盘赌选择出新食物源xi，然后对新食物源进行如雇佣蜂一致的开采并进行贪心选择。观察蜂观察食物源的替换情况，若某食物源在规定的limit次开采后均未被替换，蜂群将放弃这一食物源，并由观察蜂重新随机生成一个食物源来替代。最终算法将循环执行雇佣蜂、跟随蜂和观察蜂的操作，直至满足停止条件。

2 人工蜂群算法的改进

人工蜂群算法自提出以来，并用严格的理论来证明其搜索维数的多少，及其扰动尺度;根据经验性的研究，已确定单一的一维搜索方式使得蜂群的搜索步长较短，从而会造成其在某些问题上的收敛速度缓慢，但一维搜索方式对个体的改变量较小，使得算法对个体有更强的微调处理能力，因此人工蜂群算法收敛精度明显高于其他进化算法;本文在雇佣蜂阶段中引入一种联合搜索机制，使蜂群随机进行一维或多维搜索来克服搜索步长短的限制，同时也保留人工蜂群算法的高收敛精度;另外，针对不同的搜索维数，文中制定了不同的扰动尺度系数来配合，从而产生了两种不同的搜索方程。在跟随蜂阶段，选用一种新的选择策略，来增强种群的多样性，防止算法陷入局部最优。仿真实验表明，该策略能取得更好的收敛效果，并加快人工蜂群算法的收敛速度。

2.1 历史种群与种群初始化

标准人工蜂群算法中，种群的引导是当代种群内不同个体间的引导，为进一步增强种群多样性，利用与当代种群有更大区别的历史种群进行引导，历史种群是当代种群或以前的某一代种群，其选择是一马尔科夫链过程，每代历史种群更新情况如下

其中，历史种群记作old P，初始种群记作P，即old P可选择成为上代种群P或保持不变，选择后对old P的个体做随机排序。

改进算法的初始化包括种群初始化和历史种群初始化，初始化方程如下

其中，Pi，j，old Pi，j分别表示种群和历史种群第 i个个体的第j维元素;lowj，upj分别表示第j维分量的下界和上界;rand表示(0，1)中的随机数，两初始化过程相互独立。对历史种群的初始化是为了防止第一次搜索时，历史种群为空。

2.2 雇佣蜂的改进

2.2.1 新的搜索方式

本文引入以下搜索方式，该搜索方式既可进行多维搜索也可进行一维搜索，两者等概率随机调用，新的搜索方程如下

map是一索引矩阵，·表示矩阵点乘运算，mapi，j为0或1，当为1时，代表第i个个体的第j维为搜索维;当为0时，表示其不为搜索维。F是扰动系数，offsprings是生成的实验种群，若offsprings的第i个体适应度值大于种群P的第i个体函数值，则将用来替换种群P的第i个体。其中，old P和map在每一代均会更新，map矩阵用来控制一维搜索和多维搜索的选择，其更新方式如下

2.2.2 雇佣蜂搜索方式的改进

对于每一代雇佣蜂，进行以下开采搜索，且对于不同的搜索维数赋予不同的扰动系数。

(1)多维搜索方式时，扰动系数F的生成方程如下

epk是当前代数，epoch是最大进化代数，CH3是一服从自由度为3的卡方分布随机数，新扰动系数即可产生规模较小的量，有利于局部搜索，也可产生规模较大的量，有利于全局搜索。改进的扰动系数比原扰动系数更能平衡局部搜索和全局搜索。另外，改进扰动系数的设计参考了差分进化算法的扰动方程，将产生扰动系数的分布中心改为0.5而不是0。大量数值实验表明，分布中心改为0.5有更好的收敛效果。

(2)一维搜索方式时，扰动系数F的方程如下

此时搜索过程等价于标准人工蜂群算法的搜索过程。

2.3 跟随蜂阶段的改进

在新的跟随蜂阶段，在保证跟随蜂作用前提下改变了跟随蜂选择食物源的方式。首先计算适应度值，方程如下

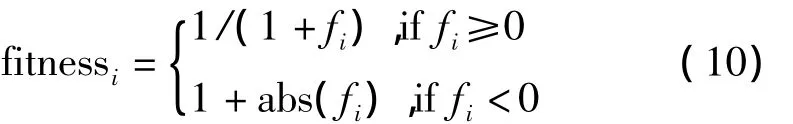
为每个食物源赋予以下选择概率

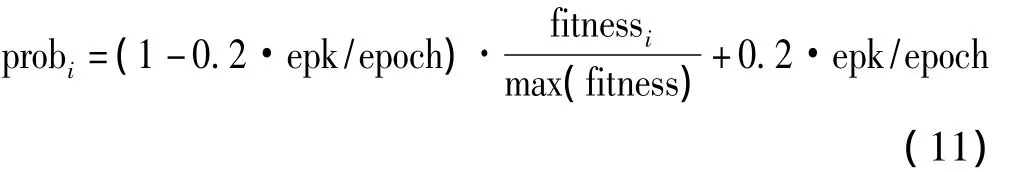
生成［0，1］间的随机数rand与probi比较大小，若有rand＜probi，对食物源i进行同雇佣蜂相同的搜索，否则不对其进行搜索;在蜜源中循环进行该操作，直到进行次ps搜索，跟随蜂阶段结束。

新的选择概率保持了具有大适应度值的可行解，有较高的选择可能性，同时随着进化代数的增加，不断提高了小适应度值可行解被选择的几率，有利于保持种群的多样性。

3 实验设计

实验设计从文献［7～8］中选取了12个多维测试函数，在相同的搜索次数下，将改进蜂群算法与标准蜂群算法的收敛时间和收敛结果进行比较，12个测试函数如表1所示。

表1 Benchmark测试函数

表2 测试实验参数取值

实验均在相同配置的计算机上，用Matlab 2013a进行编程测试。为了说明改进人工蜂群算法的收敛性能，给出5个高维函数 F1、F2、F3、F7和F8的收敛曲线，如图1所示。

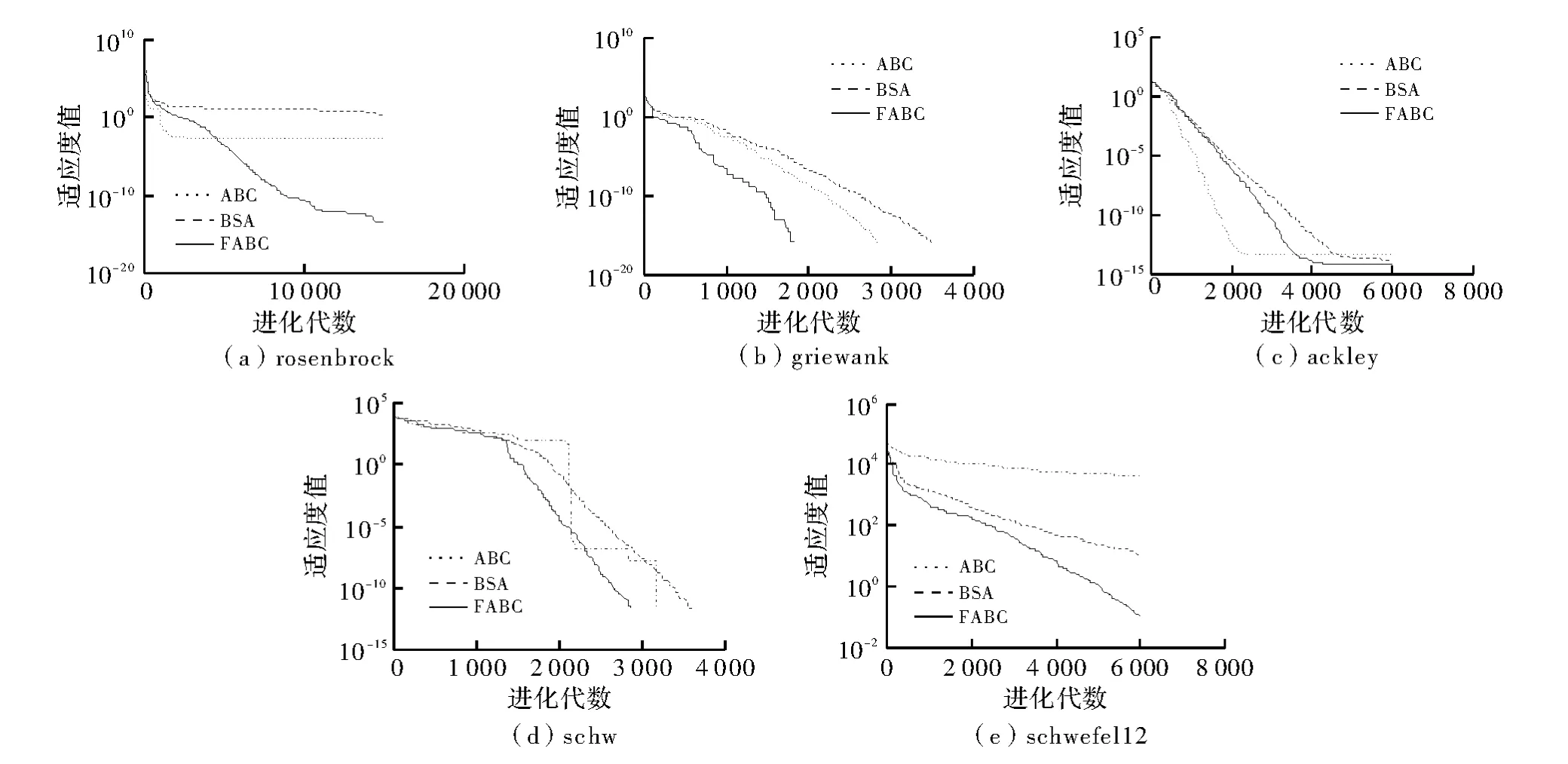
图1 收敛曲线图

改进蜂群算法、标准蜂群算法和回溯搜索算法的 收敛时间与收敛结果比较，如表3所示。

表3 改进蜂群算法与标准蜂群算法的收敛时间和收敛结果比较

从12个测试函数的结果可看出，FABC的收敛效果均优于ABC及BSA，这说明基于多维和一维混合搜索策略的改进雇佣蜂阶段，能克服单维搜索雇佣蜂收敛速度慢的缺点，缩短搜索时间，有效加快了收敛速度;即使在解决griewank等高维问题时，FABC的搜索效率也比ABC及BSA高，这一方面归功于雇佣蜂阶段更具开发性的搜索策略;另一方面得益于跟随蜂阶段有效的选择策略，充分保证了种群的多样性，使算法在加快了收敛速度时不易陷入局部最优。新的搜索策略和选择策略在加快了收敛速度的同时，也确保了算法具有较高的稳定性。

4 结束语

人工蜂群算法搜索步长过短，对某些问题存在收敛速度慢的缺点，且易陷入局部最优，回溯搜索优化算法有较强的搜索能力，其变异方程能进行长距离的扰动，且在基变量无旋转的基础上扰动，与雇佣蜂的搜索方式相似。本文借鉴BSA算法的思想对人工蜂群算法的雇佣蜂进行改进，较好地改进了单一一维搜索下的缺点，并设计了自适应的跟随蜂的选择策略，以增强算法的全局搜索能力。仿真实验表明，改进算法有更快的收敛速度和精度。

［1］Karaboga D，Basturk B.A powerful and efficient algorithm for numerical function optimization:artificial bee colony(ABC)algorithm［J］.Journal of Global Optimization，2007，39(3):459－471.

［2］暴励，曾建潮.自适应搜索空间的混沌蜂群算法［J］.计算机应用研究，2010，27(4):1331 －1335.

［3］丁海军，冯庆娴.基于Boltzmann选择策略的人工蜂群算法［J］.计算机工程与应用，2009，45(31):53 －55.

［4］Zhu G，Kwong S.Gbest－ guided artificial bee colony algorithm for numerical function optimization［J］.Applied Mathematics and Computation，2010，217(7):3166 －3173.

［5］Civicioglu P.Backtracking search optimization algorithm for numerical optimization problems［J］.Applied Mathematics and Computation，2013，219(15):8121 －8144.

［6］Storn R，Price K.Differential evolution－a simple and efficient heuristic for global optimization over continuous spaces［J］.Journal of Global Optimization，1997，11(4):341 －359.

［7］Karaboga D，Akay B.A comparative study of artificial bee colony algorithm ［J］.Applied Mathematics and Computation，2009，214(1):108 －132.

［8］Molga M，Smutnicki C.Test functions for optimization needs［J］.Journal of Global Optimization，2009，23(3):281 －287.