基于改进BP神经网络的洪峰预测模型

高丽媛，董 甲

(1.华北水利水电大学信息工程学院，河南郑州 450011;2.黄河勘测规划设计有限公司，河南郑州 450000)

BP网络因其强大的非线性映射能力，可逼近任何非线性连续函数，同时具有自学习和自适应能力等优点，国内外学者均对其进行了研究，并解决了较多应用方面的问题。随着应用范围的扩大，其缺点暴露出来，在训练过程中，网络权值易陷入局部最小化，对训练结果造成误导，当要优化的目标函数较为复杂时，收敛速度会很慢。基于这些问题，本文在前人研究的基础上提出了基于模拟退火遗传算法的改进BP神经网络，并利用黄河流域水文站数据进行洪峰测试，根据两种模型的验算数据，分析其优劣。

1 BP算法及其改进

1.1 BP算法

神经网络(Back Propagation，BP)是一种按误差逆传播算法训练的多层反馈网络，是目前应用广泛的神经网络模型之一，模型训练开始前需要设置最大训练次数c，训练终止条件E≤e，初始化网络权重wij、vjt和阈值 θj、γt，四者均为为(－ 1，1)之间的随机值。变量设置完毕后，读入训练样本并计算计算中间层的输入输出并根据公式计算输出层的输入，输出Ct=f(Lt)=涉及到输出层的一般误差Ct)Ct(1－Ct)，中间层的一般误差bj(1－bj)根据误差结果修改输出层的权值和阈值vjt(N+1)=vjt(N)+αdktbj，γjt(N+1)= γjt(N)+(－ αdkt)，以及隐层的权值和阈值wij(N+1)=wij(N)+βejai，θj(N+1)= θj(N)+(－ βej)，直至 m 个样本训练完成。此时判断全局误差是否满足E≤e，否则重新训练，直到满足要求，或达到最大训练次数［1－2］。BP网络模型其算法流程，如图1所示。

各连接权值W(k)和神经元阈值的初始值依靠随机选取，其分布范围较大，网络优化时需多次迭代才能找到最优解。鉴于此，本文提出基于遗传算法的BP神经网络，根据遗传算法的特点，减少优化时的迭代次数，提高收敛速度［3］。

图1 BP网络模型其算法流程图

1.2 改进BP神经网络

模拟退火遗传算法是以遗传算法为主体流程，引入模拟退火机制，该算法在执行时首先通过遗传算法进行全局搜索，产生出较优良的群体，再利用模拟退火算法进行局部搜索，对基因个体进行优化调整，避免了遗传算法收敛性差的缺点，可高效地找到最优解［4］。文中的改进BP神经网络先利用模拟退火遗传算法局部搜索能力强的特点，将神经网络的权值和阈值优化到一个较小的范围，然后利用BP算法进行预测［5］，从而建立成熟神经网络结构，两种算法的结合能显著提高BP网络的性能。

GA －BP 算法具体［6－8］步骤如下:(1)选择适应度函数，模拟退火遗传算法叙述要利用该函数确定种群个体适应度大小，以此判断个体是否被选择。(2)初始化网络参数，并给出训练参数。由rand函数产生一组(－1，1)之间的随机数确定，选择训练结果最好的一次作为网络的初始权值和阈值，网络的训练参数按照模拟退火遗传算法进行预处理，表示成二进制编码的形式。(3)计算种群个体的适应度及总适应度，若达到预定值则转至步骤(5)，否则执行步骤(4)。(4)采用模拟退火遗传算法对种群进行进化，对种群个体进行相应的选择、交叉和变异操作，繁殖过程采用最优个体保留策略，选择优异个体组成优异群体，直到群体的适应度趋于稳定，完成后转至步骤(3)。(5)使用BP网络进行迭代计算，若未达到全局误差要求，则转至步骤(4)，否则执行步骤(6)。(6)输出此时的种群，即网络权值和阈值。(7)输出对应的匹配结果。

GA－BP网络流程如图2所示。

图2 GA－BP网络流程图

2 实验分析

以黄河流域潢川水文站、淮滨水文站、泌阳水文站逐日流量及逐日区间雨量数据为例，分别采用BP神经网络和GA－BP神经网络模型进行洪峰预测，对比说明GA－BP网络的可行性和优越性。表1中前10组数据作为训练数据，后5组作为测试数据。

表1 前10组数据作为训练数据

续表1

2.1 BP神经网络模型运行

BP神经网络输入元需先经归一化处理，分别为潢川水文站流量、淮滨水文站流量、区间雨量和区间净雨量，隐层节点数根据经验公式为输入层节点数，n0为输出层节点数，a为1～10之间的常数)，输出层为一个神经元，输出值为泌阳水文站流量归一化数值，采用newff函数创建网络，设定训练误差为1e－5，训练次数为1 000次。网络设置完成后，使用BP神经网络模型进行训练，训练完成后，将其用于流量预测，得到的数据与真实数据进行比较，表2为泌阳水文站BP神经网络模型下预测流量与实际流量的对比。设Q为模型演算值Qi与实际流量值Qs之间的误差，根据误差公式Q=(Qi－Qs)/Qs×100%，对样本进行统计。

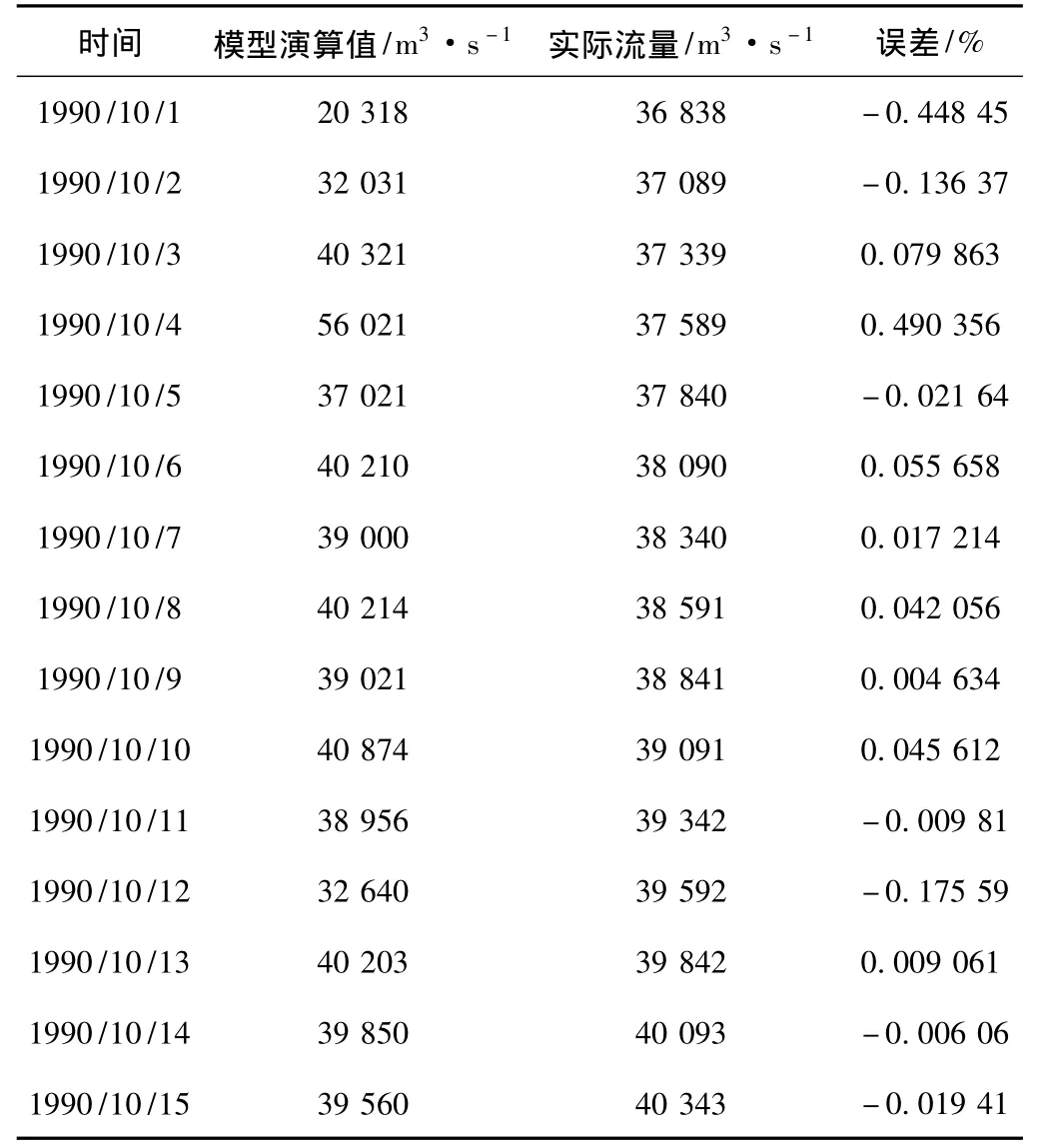
表2 泌阳水文站BP神经网络模型下预测流量与实际流量对比

由表2可看出，BP神经网络模型最大误差为0.49%，最小误差为－0.45%，根据公式，得平均绝对值误差为1.56%。

2.2 改进的BP神经网络模型

基于模拟退火遗传算法BP网络模型输入层和输出层同样需要经过归一化处理，与原始BP神经网络模型设定相同，隐层节点数采用经验公式进行设定，设定为4，遗传群体数目初始化为10，同样设定训练误差为1e－5，公式训练参数、个体适应度及总适应度、阈值等均在实验过程中不断进行调试，以取得满意效果。模型仍采用表1数据，表3为泌阳水文站GA－BP神经网络模型下预测流量与实际流量的对比。

表3 泌阳水文站GA－BP神经网络模型下预测流量与实际流量的对比

根据表3数据和平均绝对误差公式0.88%。由此可见，改进的BP网络模型演算数据与实际数据更为接近，误差控制在更小的范围内。同时模拟退火遗传算法对初值的引进，减轻了BP网络的负担，缩短耗时。

3 结束语

使用模拟退火遗传算法优化BP神经网络，主要包括优化网络结构、优化权系数、优化网络结构和学习规则等［4］。由实验结果对比可以看到，BP网络和模拟退火遗传算法的结合，在程序运行上减小了搜索空间、提高了算法的搜索效率，结果更为精确，缩小了误差范围。

［1］王鹏.基于数据挖掘的洪峰预测系统的研究与实现［D］.南京:河海大学，2006.

［2］陈云翔.防洪决策中洪水灾情智能预测与评估模型的研究［D］.上海:东华大学，2008.

［3］丁永生.计算智能理论技术与应用［M］.北京:科学出版社，2004.

［4］张晖，吴斌，余张国.引入模拟退火机制的新型遗传算法［J］.电子科技大学学报:自然科学版，2003，32(1):39－42.

［5］穆阿华，周绍磊，刘青志，等.利用遗传算法改进BP学习算法［J］.计算机仿真，2005，20(2):150－151.

［6］李维良，叶三星.遗传BP算法在双色球彩票预测中的应用［J］.软件导刊，2011，10(11):81 －83.

［7］石争浩，黄士坦，冯亚宁，等.遗传算法和BP算法相结合进行图像匹配［J］.武汉大学学报:工学版，2003，36(3):91－94.

［8］陈伟涛，杨沛，刘朝阳，等.BP神经网络在雷达目标识别中的应用［J］.电子科技，2010，23(12):18 －19.