基于蒙特卡洛方法的线性混合效应状态空间模型

唐爱萍

(西安电子科技大学数学与统计学院，陕西西安 710071)

状态空间模型［1］是一个重要的分析模型，在经济、工程、医学等领域发挥着重要作用。而线性状态空间模型是应用广泛的状态空间模型，尤其是在时间序列及控制数据中，较多数据模型如ARMA模型等均可转化成线性状态空间模型。对于参数已知的高斯线性状态空间模型，卡尔曼滤波［2］是一种非常有效的状态估计算法。除此之外，文献［3］首先提出了运用序贯蒙特卡洛的方法解决状态的估计问题。

纵向数据［4－5］的应用广泛，将其引入到线性状态空间模型中具有较大应用价值，但需克服的困难是如何处理高维数据以及同时实现每个个体的状态估计问题。文献［6］将个体参数当做隐变量，引入到混合效应方程［7］中，从而形成对混合效应状态空间模型(Mixed － Effects State Space Model，MESSM)的研究［7］，加入隐变量到线性状态空间模型后，此时模型变为非线性状态空间模型。对于非线性状态空间模型［8－9］，目前国内外已提出的方法有扩展卡尔曼滤波等算法，但却均不是最优的解决非线性状态空间模型的最优算法，且始终没有新的研究进展。而对于非线性混合效应状态模型的研究则更少。

文献［6］分别将状态变量分为总体和个体的来研究，但前提是要应用预测的个体参数，这增加了状态估计的成本。因此对于纵向数据的状态空间模型，研究出一种无需直接估计个体参数而进行状态估计的方法，将进一步提高MEMSE的应用价值。

1 线性混合效应状态空间模型

线性混合效应状态空间模型是状态空间模型的扩展，其是在状态空间模型式(1)和式(2)基础上增加了随机效应方程(3)。基于本文要研究的纵向数据，给出第i(i=1，2，…，n)个个体的线性MESSM

其中，xit，yit分别表示时刻t第i个个体的p×1状态变量和q×1观测变量;H(θi)，G(θi)分别是 p×p状态转移矩阵和q×p观测矩阵，且含有未知参数θi;vit，wit分别是维数为p×1，q×1的状态噪声和观测扰动，当i=j且 t=t'时，Cov(vit，vjt')=Q，Cov(wit，wjt')=R，其余情况均等于0。式(3)中eθ是固定效应，bi是随机误差。对于正态的线性状态空间模型，卡尔曼滤波算法可实现状态xt最小无偏的在线估计。

2 基于序贯蒙特卡洛算法的状态估计

对于线性 MESSM，设 Yit≜{yi1，yi2，…，yit}表示第i个个体截止时刻t的所有观测数据的集合，此部分讨论参数已知，给定观测数据{Yit}mi=1时，通过卡尔曼滤波与蒙特卡洛方法的结合实现对MESSM中状态的估计问题，在此重点讨论状态的一步向前预测估计问题，其他情况均可由滤波算法推导。

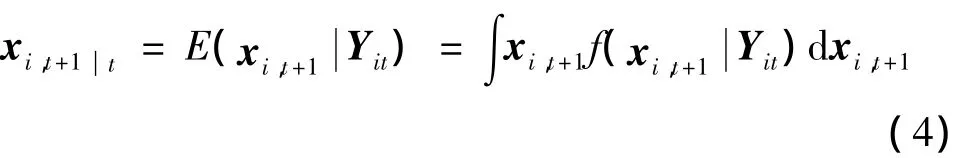
f(xi，t+1是状态变量xi，t+1的条件概率密度函数，式(4)可进一步的写为

其中，f(θiYit)是θi的后验分布。进一步，由条件方差公式可得 xi，t+1的方差满足

则由式(5)和式(6)可得出，只要给定θi，条件期望和条件方差可由卡尔曼滤波公式［1］计算得到。若从 f(θi中进行抽样得到样本集{θ(ij)}Nj=1，由

对于每一个 θ(j)i(j=1，2，…，N)，由卡尔曼滤波迭代公式可得

由以上分析可得出，对于线性MESSM，在随机效应θi未知时，将序贯蒙特卡洛重要性抽样方法与卡尔曼滤波算法相结合，可实现对状态的在线估计问题。具体做法如下:

(1)初始 t=0，假设初始状态x0服从正态分布N(a0，P0)，其中 a0，P0已知。从先验分布 g(θi)中产生随机样本集{θ0(j)}Nj=1，且参数 θ0(j)有权重 ω0(j)=，(j=1，2，…，N)，对于每个参数 θ0(j)一步向前预测

(2)时刻 t=1，对于每个参数 θ0(j)，用 Ω(tj)=表示相应参数θ(tj)的卡尔曼滤波估计值。假设在 t－1 时刻，有观测数据 Yi，t－1，有粒子集{θ(t－j)1}Nj=1服从后验分布，则对于每个 θ(t－j)1，对应时刻的状态估计值 Ω(t－j)1也可得到，从而由式(6)和式(7)可得

(3)在时刻 t=2，3，…，当得到新的观测数据 Yi，t=(yi1，…，yit)，对于 θ(t－j)1更 新 Ω(tj)。更新权重 w(tj)=然后从集合以概率产生随机样本

3 仿真数据的研究

为进一步验证上文提到算法的有效性，对线性MSE模型进行仿真实验。对于式(1)～式(3)，H(θi)=θi，G(θi)=1 设参数已知，取 eθ=0.8，D=0.006 4，Q=1，R=0.8，m=50，时间分别取T=20 和 T=40，从而产生了两组模拟数据。为便于比较，在个体随机效应θi已知情况下运用卡尔曼滤波算法进行状态的估计，而在其未知时运用序贯蒙特卡洛滤波算法做状态的估计。在运用蒙特卡洛滤波算法进行状态估计时，对于每组模拟数据，分别取3组抽样样本 N=100，200，500。最终仿真结果如表1、图1和图2所示。

在表1中分别发给了在不同时间及不同采样数下，两种算法的均方误差的比较数据;在图1和图2中给出了两种算法状态估计值以及估计根均方误差(RMSE)的比较结果，图中标注的ss(t)表示模拟出的真实状态值，X1(t)，kf1(t)分别表示用蒙特卡洛滤波方法和卡尔曼滤波算法得到的状态估计值，RMSE1，RMSE2分别表示两种方法的RMSE。

表1 蒙特卡洛滤波和卡尔曼滤波算法均方误差的比较

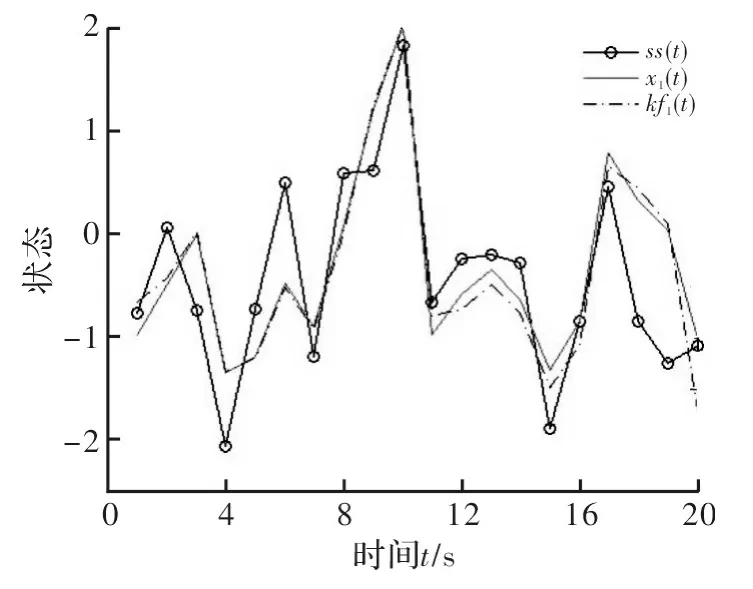
图1 T=20时蒙特卡洛滤波与卡尔曼滤波结果比较

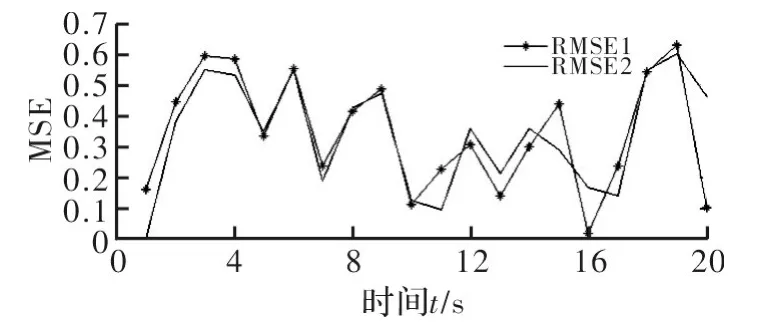
图2 T=20时蒙特卡洛滤波与卡尔曼滤波RMSE

从表1、图1和图2的结果可看出，在同样的数据下，两种方法的估计结果相差较小。因此，对于混合效应的状态空间模型，在随机效应未知的情况下，本文提到的蒙特卡洛滤波算法是一种有效的状态估计方法。本例中用到的线性模型虽较为简单，但也容易拓展到高维线性模型中。同时，对于非线性状态空间模型，只要可运用线性化技术转化为MESSM，在个体参数未知的情况下，本文中提到的方法也可以做状态的在线估计问题。

［1］James Durbin.Times series analysis by state space methods［M］.US:Oxford University Press，2001.

［2］Harold W Sorenson.Kalman filtering:theory and application［M］.USA:IEEE Press，1985.

［3］Jun S Liu，Rong Chen.Sequential monte carlo methods for dynamic systems［J］.Journal of the American Association，1998，93(443):1031 －1044

［4］Mun J，Lindstrom M J.Diagnostics for repeated measurements in linear mixed effects models［J］.Statistics in Medicine，2013，32(8):1361 －1375.

［5］Liu D，Lu T，Niu X，et al.Mixed － effects state － space models for analysis of longitudinal dynamic systems［J］.Biometrics，2011，67(2):476 －485.

［6］Jun S Liu.Monte carlo strategies in scientific computing［M］.Germany:Springer，2002.

［7］Shayler Searle，George Casella.Variance components［M］.America:Wiley － Interscience，2011.

［8］Pedersen M W，Berg C W，Thygesen U H.Estimation methods for nonlinear state － space models in ecology［J］.Ecological Modelling，2011，222(8):1394 －1400.

［9］Zhou J，Han L，Liu SY.Nonlinear mixed － effects state space models with applications to HIV dynamic［J］.Statistics and Probability Letters，2013，83(5):1448 －1456.

［10］Huang Y X，Liu D C，Wu H L.Hierarchical bayesian methods for estimation of parameters in a longitudinal HIV dynamic system［J］.Biometrics，2006，62(2):413 －423.

［11］Markus Hurzeler，Hans R Kunschk，Monte Carlo.Approximations for general state － space models［J］.Journal of Computational and Graphical Statistics，1998，7(2):175 －193.

［12］Jun SLiu.Metropolized independent sampling with comparisons to rejection sampling and important sampling［J］.Statistics and Computing，1996，6(2):113 －119.