基于混沌理论的电力系统谐波检测
2015-12-20李兆旸刘崇新燕并男
李兆旸,刘崇新,燕并男
(西安交通大学 电气工程学院,陕西 西安 710049)
电网中的谐波问题对电力系统的安全、稳定、经济运行构成了极大的潜在威胁,为了能把注入公网的谐波电流以及谐波电压控制到安全范围内,首要解决的问题就是谐波检测。谐波检测的传统方法主要有模拟滤波器测量谐波法,基于瞬时无功功率理论的谐波检测法,基于傅里叶变换的谐波检测法以及基于神经网络理论的谐波检测法等[1]。但是上述传统方法中,由于信号中常常包含噪声,其直接增大了仿真结果的误差,影响了精确性。为此,通过混沌系统来检测电力系统谐波信号,利用其对小信号极强的敏感性以及对噪声的强免疫能力来解决传统检测方法中对噪声抑制不彻底的不足之处,作为对现有谐波信号检测方法中的一个补充是很有必要的。
混沌检测不同于现有传统的电力系统谐波检测方法,它利用了混沌系统对于初值的极度敏感性,即我们可以考虑将h次谐波视为微扰信号,通过检测系统状态就可以根据其是否发生极大的变化来判定该谐波信号是否存在,若系统状态变化时,还可以通过观察系统状态变化的特征,并对信号做出适当的处理以及运算,求出被测信号的各种参数[2-4]。
目前,Duffing振子[5]因其间歇混沌现象的特性常被用来作为检测谐波信号的模型。具体来说,在Duffing方程右侧加入与内置信号频率差较小的待测信号时,内置信号幅值会出现相应变化,系统由于幅值的逐渐增大,会出现相应的间歇性混沌现象。即时而周期,时而混沌的运动状态。经研究发现,当幅值的变化到达某一临界值时(即系统出现临界混沌状态时),系统将在大尺度周期状态和混沌状态两者之间振荡,即会出现间歇性混沌现象,当幅值继续增大时,系统将由间歇性混沌发展为混沌。
本文对Duffing振子方程进行了改进,分析了其产生的间歇混沌现象。通过仿真实验证明:它对噪声和与内置信号频差较大的周期干扰信号具有较强的免疫力,并根据产生这种现象的机理,提出了一种新的有效检测电力系统谐波信号的方法。
1 利用混沌性质检测信号的原理
Duffing方程在非线性动力学系统具有重要的地位,根据其方程形式确定的混沌系统具有丰富的动力学特性。其具体形式如下:

式中,x(t)为状态变量;k为阻尼比;f为周期策动力幅值;-x(t)+x3(t)为非线性恢复力。
以往对Duffing方程检测的研究中[6-11],使用的均是式(1)的方程形式。经对比发现,若将方程中的非线性恢复力项x幂项的系数增加,将显著提升系统检测信号的灵敏度以及工作稳定性。改正后的方程形式如下:
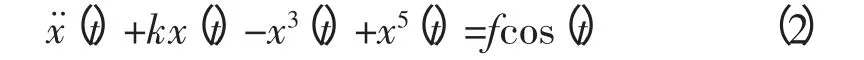
改写为动力学方程:

对Duffing振子进行仿真分析,观察其动力学行为。
若振子方程中的阻尼比k固定,则系统状态随着f 的变化如下:
f=0时,系统相轨迹图中鞍点为(0,0),两个焦点分别为(1,0)和(-1,0),而点(x,x.)最终停在两焦点之一,如图1所示。
当f≠0时,系统随f 取值的不同而呈现出不同的动力学形态。当f 较小时,相轨迹表现为小周期运动状态,相点只围绕一个焦点做周期振荡。f 逐渐增大的同时,系统会依次呈现出同宿轨道状态(如图2所示)和分叉状态(如图3所示),直到达到混沌状态(如图4所示),上述过程中f 的变化非常迅速。而在系统达到混沌状态以后,调节策动力幅值时发现,系统在较大的一个区间内都将呈现出混沌状态。继续增大f,当其达到某个分叉阈值fd时,系统将会处于由混沌运动转为周期运动的临界状态(又称临界混沌状态),如图5所示。这时只需极小地增加f,使其值仅仅大于分叉阈值fd时,系统就进入大尺度周期状态,如图6所示,此时相轨迹将焦点、鞍点统统围住。

图1 f=0,[x(0),x′(0)]=[1,1]Fig. 1 f=0,[x(0),x′(0)]=[1,1]

图2 f=0.2,[x(0),x′(0)]=[0,0],w=1 rad/s同宿轨道状态Fig. 2 f=0.2,[x(0),x′(0)]=[0,0],w=1 rad/s homoclinic orbit state
取阻尼比k=0.5,将策动力幅值从0逐渐增大,采用变步长ode45数值算法,即龙格库塔方法进行仿真。各个状态的时域波形图以及相轨迹图如图1—6所示。
仿真结果表明了Duffing振子的动力学行为,并且从图5到图6的变化中可以看出,策动力幅值极其微小的变化(10-8)就能引起系统状态产生质的变化。由以上分析可以得知,我们可以利用相轨迹由周期振荡到混沌运动或者由混沌运动到周期振荡的显著变化来检测信号,可以发现,这种变化对策动力信号幅值极具敏感性且对噪声具有较强的免疫力等特点可以作为我们检测谐波的基础。据此,首先调节策动力幅值f,使Duffing振子系统处于混沌状态向大尺度周期状态过渡中的临界混沌状态,将谐波信号也就是待测信号作为Duffing振子周期策动力的扰动,将其相加从而作为驱动力。由于该系统对策动力的扰动极其敏感,通过观察系统状态发生改变与否,可以检测出谐波信号是否存在,从而测定出该信号的参数。
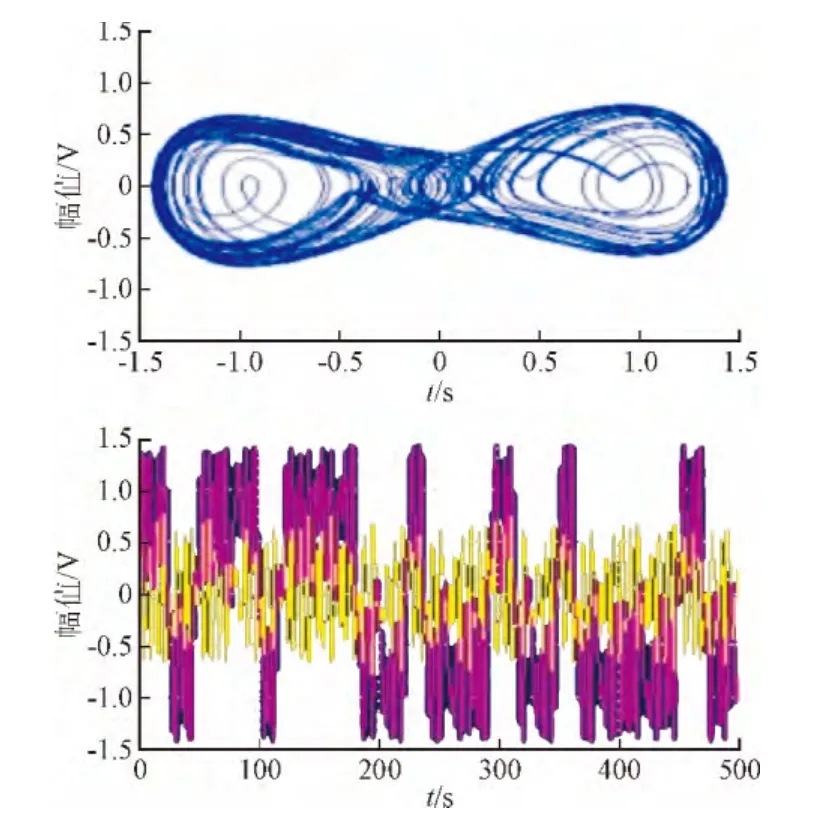
图3 f=0.4,[x(0),x′(0)]=[0,0],w=1 rad/s分叉状态Fig. 3 f=0.4,[x(0),x′(0)]=[0,0],w=1 rad/s bifurcation state

图4 f=0.6,[x(0),x′(0)]=[0,0],w=1 rad/s混沌状态Fig. 4 f=0.6,[x(0),x′(0)]=[0,0],w=1 rad/s chaotic state
2 测定信号参数
令t=ωτ,f=F0,式(1)可以改为:

图5 f=0.736 882 42,[x(0),x′(0)]=[0,0],w=1 rad/s临界混沌状态Fig. 5 f=0.736 882 42,[x(0),x′(0)]=[0,0],w=1 rad/s the critical state of chaos

图6 f=0.736 882 43,[x(0),x′(0)]=[0,0],w=1 rad/s大尺度周期状态Fig. 6 f=0.736 882 43,[x(0),x′(0)]=[0,0],w=1 rad/s large-scale periodic state
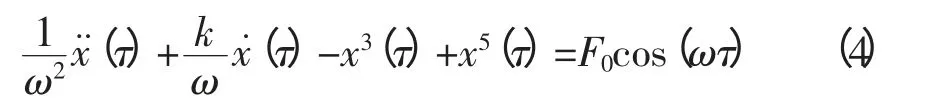
在式(4)中右侧加入频率在ω附近的待测信号f′(t)=Acos[ω(1+Δω)t+φ],(Δω为待测信号与原有周期信号之间的相对频差),得到:
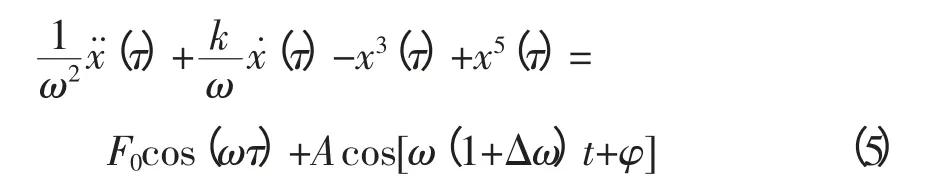
等号两边同时乘以ω2并对右侧简化,得到:

上式中
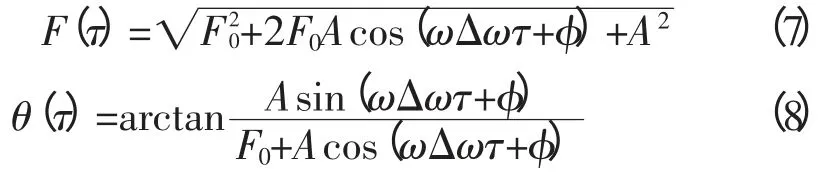
式中,F(τ)为驱动力的幅值;θ(τ)为驱动力的初相角。由于A垲F0,所以θ(τ)的影响可以忽略。
观察式(6)与式(2)发现,二者差除了系数ω之外,前者比后者还多出了一个相位角参数。
据此,可得以下结论:
1)当Δω=0时,它表示此时待测信号频率与周期策动力信号频率相同。
2)当Δω≠0时,策动力信号频率与振动信号频率之间会有一个微小的频差。此时总策动力F(τ)的幅值会在F(τ)∈(F0-A,F0+A)区间内周期性地交替变化,由于参考信号矢径与外加信号矢径方向趋于一致或方向相反时直接影响总驱动力F(τ)的幅值,即系统受F(τ)值的影响,时而大于fd而进入周期状态,时而小于fd而进入混沌状态,从而出现间歇性混沌现象。在微小的角频差情况下,系统将以T=2π/Δω为周期,进行间歇性混沌运动。因此可以通过测量T,间接得到外界待测信号的频率值。
取F0=0.72,A=0.04,ω=1.00,Δω=0.05,观察系统变化情况。发现系统处于时而混沌运动,时而大尺度周期运动状态,即出现间歇性混沌现象,如图7所示。

图7 Δω=0.05的间歇性混沌现象Fig. 7 Intermittent chaos in Δω=0.05
由图7、图8对比观察,当待测信号与原有周期信号的相对频率差值Δω过大时,间歇性混沌现象逐渐变得不明显或者消失,因为系统完成状态变化通常需要1个周期以上的时间,当Δω过大时,由式(7)决定的F(τ)变化过快,激励不足以持续足够长的时间,使得系统无法在状态转变时响应驱动力值F(τ)快速的变化,导致间歇性混沌现象不再规律性地出现。另外,当Δω过小时,F(τ)在相当长的一段时间内变化很小,导致系统状态变化所需要的时间很长,即在一段长时间内维持周期状态或混沌状态。通过仿真实验,我们一般取Δω∈(0.02,0.06)才能产生明显的间歇性混沌现象。

图8 Δω=0.1的间歇性混沌现象Fig. 8 Intermittent chaos in Δω=0.1
2.1 测定信号的频率

考虑到算法效率的问题,这里用统计系统变量过零时间点的间距方法来判断系统运动的状态。因为系统处于周期状态时,过零时间点必然呈等差数列排列即间距相等,而处于混沌状态时,则不具有这样的特征。

图8的仿真和结论已经说明:当待测信号与周期策动力间的相对频率差过大时,间歇性混沌现象消失。基于这一结论,要想测定某一已知频率附近的扰动信号频率,可以把周期信号设为该已知频率,再来搜索确定该频率附近是否存在小的扰动信号,即监测间歇性混沌现象是否发生。需要注意的是搜索区间大小一定要适中,过大或者过小都会导致无法监测到明显的间歇性混沌现象。
例如要检测频率ω′∈(ω1,ω2)的待测信号,先选取合适的公比q=1+Δω,从ω1开始取ω′,ω′q,ω′q2等作为周期策动力的频率,若发生间歇性混沌现象,就用上述方法算出ω′,若没有发生间歇性混沌现象,则说明待测信号的频率不属于该预估区间内。
2.2 测定信号的相位
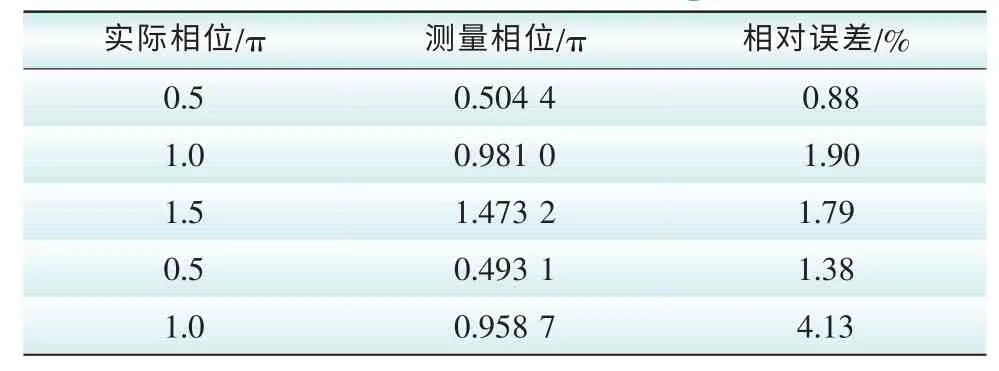
设当cos(ωΔωt+准)=a(a∈0,1)时,F(τ)=Fd(Fd为系统状态变化的临界值),则当cos(ωΔωt+准)>a时,系统会处于大尺度周期状态,对应于图9中的T1时间段;而当cos(ωΔωt+准) 图9 系统分别处于大尺度周期和混沌状态的时间段Fig. 9 System in Large-scale periodic state and chaoticstate period 设式(5)中的周期策动力为F0cos(ωt+准1),待测信号Acos(ω(1+Δω)t+准2),二者相位差Δ准=准2-准1,F(τ)和θ(τ)均有变化: 不妨设相位差Δ准=0,当t=0时,cos(ωΔωt+Δ准)=1,F(τ)=F0+A>Fd,系统处于大尺度周期状态,随着时间的变化,ωΔωt+Δ准=T1时,cos(ωΔωt+Δ准)减小到a,F(τ)从F0+A减小到Fc,系统处于从大尺度周期状态进入混沌状态的临界状态。同样的,如果cos(ωΔωt+准)从a增加到1,相应的F(τ)从Fc增加到F0+A,不难发现,该过程同样需要时间T1。 图10 Δφ不同时的间歇性混沌现象Fig. 10 Intermittent chaos in different phase Δφ 待测信号相位准2=准1+Δ准。 观察图9可得: 上两式中,T1为大尺度周期状态的持续时间;T2为混沌状态的持续时间。 通过过零点间距方法找出大尺度周期状态和混沌状态的持续时间T1和T2,代入式(14)中解关于幅值A的一元二次方程,即可得到未知信号幅值的大小。 仿真试验中的振子实验结构如图11所示。 图11 振子的系统仿真模型Fig. 11 Oscillator system simulation model 当将待测信号加入原有周期信号之后,通过检测间歇性混沌信号,并用上述方法得出待测信号的幅值。仿真时,设定k=0.3,取[x(0),x′(0)]=[0,0],利用定步长h=0.01四阶龙格—库塔方法进行计算。以下表1~表3即是仿真后所测得的信号参数。 表1 待测信号幅值Tab. 1 Amplitude of tested signal 表2 待测信号相位Tab. 2 Phase of tested signal 由仿真结果可以看出,绝对误差的总体趋势是随着测量值增加而线性上升的,而相对误差则一直维持在一个较小的值,计算结果的误差达到了测量的预期。理论上只要选择合适的参数以及算法,测量的精度上限可以无穷逼近实际值。 表3 待测信号频率Tab. 3 Frequency of tested signal 通过以上仿真分析,利用混沌系统检测电力谐波较之于传统电力系统检测方法精度更高,抗噪性更强,而当多频信号检测时,只需要调整振子参数,就可以实现检测。同时,修改方程后的振子系统比传统的Duffing振子系统对周期性小信号更具有敏感性,能够得到更大的幅值有效区间和更高的精度。若能够有效地将该方法与其他方法相结合,优势互补,将会使得利用混沌理论检测电力系统谐波走向实际应用。 [1] 李圣清,朱英浩,周有庆,等. 电网谐波检测方法的综述[J]. 高电压技术,2001,30: 39-42.LI Shengqing,ZHU Yinghao,ZHOU Youqing,et al. The overview of detecting methods for harmonic in power system[J]. High Voltage Engineering,2001,30: 39-42(in Chinese). [2] OTT E GREBOGI C,YORKE A. Controlling chaos[J].Phys Rev Lett A,1990,64: 1796-1799. [3] YANG J Z,QU Z L,HU G. Duffing equation with two periodic forcings: The phase effect[J]. Phys Rev Lett A,1996,53(5). [4] 柴旭生,文习山,关根志. 一种高精度的电力系统谐波分析方法[J]. 中国电机工程学报,2003,23(9): 35-39.CHAI Xusheng,WEN Xishan,GUAN Genzhi. A high precision method for power system harmonic analysis[J].Proceedings of the CSEE,2003,23(9):35-39(in Chinese). [5] 翟笃庆,刘崇新,刘尧,等. 利用阵发混沌现象测定位置信号的参数[J]. 物理学报,2010,59(2): 816-825.ZHAI Duqing,LIU Chongxin,LIU Yao,et al. Determination of the parameters of unknown signals based on intermittent chaos[J]. Acta Physica Sinica,2010,59(2):816-825(in Chinese). [6] HUANG J C,JING Z J. Bifucation and chaos in the three-well Duffing system with one external forcing[J].Chaos,Solitons & Fractals,2009,40(3): 1449-1466. [7] 李月,杨宝俊,石耀武. 色噪声背景下微弱正弦信号的混沌检测[J]. 物理学报,2003,52(3):526-530.LI Yue,YANG Baojun,SHI Yaowu. Chaos-based weak sinusoidal signal detection approach under colored noise background[J]. Acta Physica Sinica,2003,52(3): 526-530(in Chinese). [8] WANG Guanyu,CHEN Dajun,LIN Jianya. The application of chaotic oscillators to weak signal detection[J]. IEEE Transactions on Industrial Electronics,1999,46(2): 440-444. [9] 王永生,肖子才,孙瑾,等. Duffing混沌系统电路仿真研究[J]. 电力与系统学报,2008,13(1): 133-135.WANG Yongsheng,XIAO Zicai,SUN Jin,et al. Simulation and experimental study on the chaos circuit of Duffing oscillator[J]. Journal of Circuit and System,2008,13(1):133-135(in Chinese). [10] 聂春燕,徐振忠. 混沌系统在弱检测信号检测中的应用[J]. 传感器技术,2003,22(1): 55-57.NIE Chunyan,XU Zhenzhong. Application of chaotic system in detecting weak signal[J]. Journal of Transducer Technology,2003,22(1): 55-57(in Chinese). [11] 朱志宇,姜长生,张兵,等. 基于混沌理论的微弱信号检测方法[J]. 传感器技术,2005,24(5): 65-68.ZHU Zhiyu,JIANG Changsheng,ZHANG Bing,et al.Weak signal detection based on chaotic theory[J]. Journal of Transducer Technology,2005,24(5):65-68(in Chinese).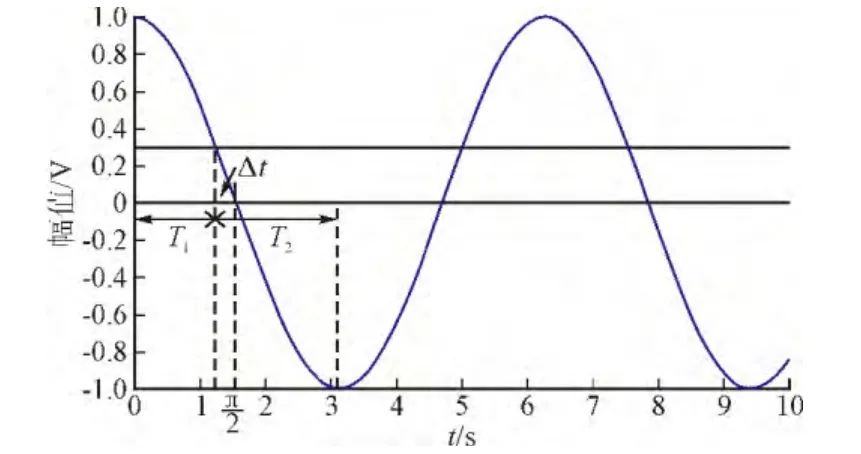




2.3 测定信号幅值



3 仿真结果



4 结论
