几种新型主动声呐发射信号性能分析研究

李玉强，杜选民，周胜增

(上海船舶电子设备研究所，上海201108)

0 引 言

声呐波形是主动声呐系统设计的三大要素之一，声呐波形一旦确定，系统的信号处理方案、时延/频移分辨力、抗混响能力、目标跟踪性能等也都基本确定，故信号波形在主动声呐设计中有着举足轻重的作用［1-2］。

随着冷战的结束，世界各主要海军大国把水声领域研究重点从深海大洋转移到浅海近岸水域，由于浅海水域水声环境复杂多变，混响干扰比深海要严重的多，严重限制了主动声呐的探测距离，抗混响是主动声呐亟待解决的关键技术。由于发射信号波形的设计是克服混响限制的有效手段，对于新型探测信号波形的设计一直是水声工作者研究的重点。除了声呐系统常用的正弦信号(CW)和线性调频信号(LFM)，正弦调频信号(SFM 信号)，调频脉冲串信号(PTFM 信号)，线性调频-巴克码组合信号(LFM-Barke 码信号)等新型的组合信号是时下研究的热点。本文通过分析发射波形模糊度函数、Q 函数比较了这几种新型主动声呐波形的时频分辨力及抗混响性能，为声呐波形选择提供了参考和依据。

1 信号的模糊度函数分析

1.1 模糊度函数的定义

信号的模糊函数［2］是具有多普勒频移和时延差信号的自相关函数，也称时间频率联合自相关函数，体现了信号能量沿多普勒频移(速度)与时延(距离)上的分布，也表征了信号多普勒频移(速度)与时延(距离)分辨能力。反映了波形受到传播延时和运动多普勒频偏的影响下通过匹配滤波器后的输出，可表征声呐系统匹配滤波处理的效果。通过对比不同信号的模糊图，可以得到其在混响条件下接收端的匹配滤波效果。模糊度图的主瓣宽度表征信号对目标的探测精度，即时频分辨力，旁瓣的高度决定了此信号在混响限制下对于多目标的探测能力。

宽带回波信号的模糊度函数

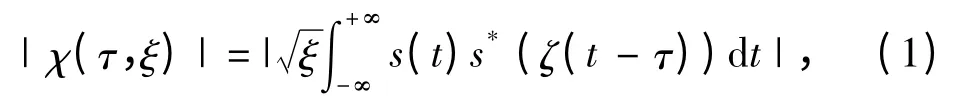
式中，ζ 为多普勒压缩因子，其定义为

式中:c 为水中声速;v 为目标速度，τ 为时延因子。

窄带回波信号的模糊度函数

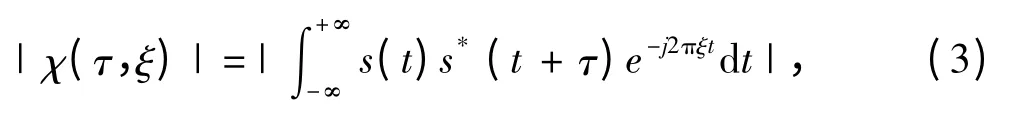
式中:ξ 为信号的多普勒频移，其定义为

式中:f0为信号的中心频率。

1.2 信号的表达形式

1.2.1 单频矩形脉冲信号

单频矩形脉冲［3］的时间函数可以表示为

1.2.2 线性调频信号

线性调频信号(LFM 信号)［4］的时间函数可表示为

其瞬时频率为

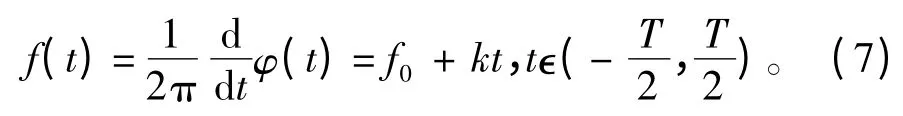
式中:K=F/T 为信号频率变化率(调频斜率)，F 为信号的调频宽度。

1.2.3 正弦调频信号

正弦调频信号(SFM 信号)［5-6］是一种由多个窄带信号构成的宽带信号，兼具宽带与窄带信号的优点。其时间函数可写为

式中，mf= Δf/2fm为调制数，fm为调制频率，Δf 为频偏。

1.2.4 调频脉冲串信号

调频脉冲串信号(PTFM 信号)［7-8］是使用LFM信号作为子脉冲，与周期脉冲卷积得到的信号，时域上相当于LFM 信号连续重复N 次，N 值与梳状谱密度有关。其时间函数可以表示为

其中，Tp=T/N。

1.2.5 线性调频- Barker 码信号

相位编码信号是利用载波相位的变化来表达信息的信号形式，Barker 码作为一种常用的二相编码信号，在雷达信号处理中被广泛研究和应用。

LFM-Barker 码复合声呐信号是线性调频信号和Barker 码相位编码信号组合而成的信号［9］，是在相位编码信号每个码元内进行线性调频信号调制而成的一种新型复合信号。

LFM-Barker 信号的复包络可表示为线性调频复包络与Barker 码相位信号复包络的卷积形式，即

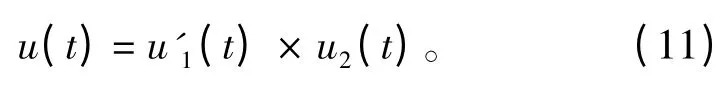
式中:

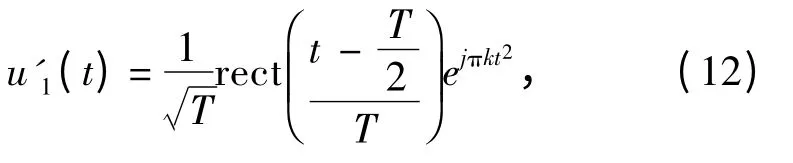
是LFM 信号的复包络，T 为线性调频时间，K= F/T为调频斜率，F 为调频带宽;

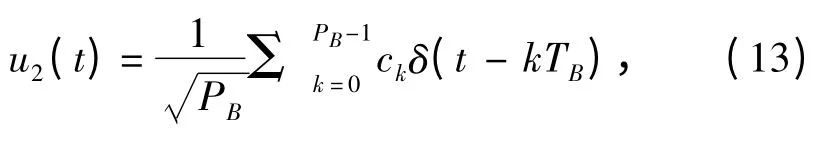
是巴克码信号的复包络，PB为码长，{c(n)}为巴克码序列，TB为巴克码一个码字的时间宽度。

1.3 信号的模糊度函数对比分析

SFM，PTFM，LFM -Barker 码信号的模糊函数如图1 ～图3 所示。

各信号共同具有参数为:信号脉宽10 ms，中心频率10 000 Hz，采样率61 400 Hz。其中LFM，SFM，PTFM，LFM - Barker 码信号的带宽为1 500 Hz，SFM，PTFM 信号频率间隔为300 Hz。

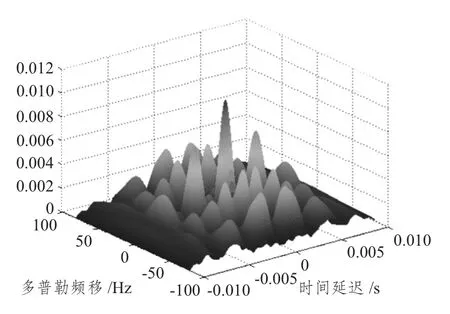
图1 SFM 信号模糊函数Fig.1 Ambiguity function of SFM signal

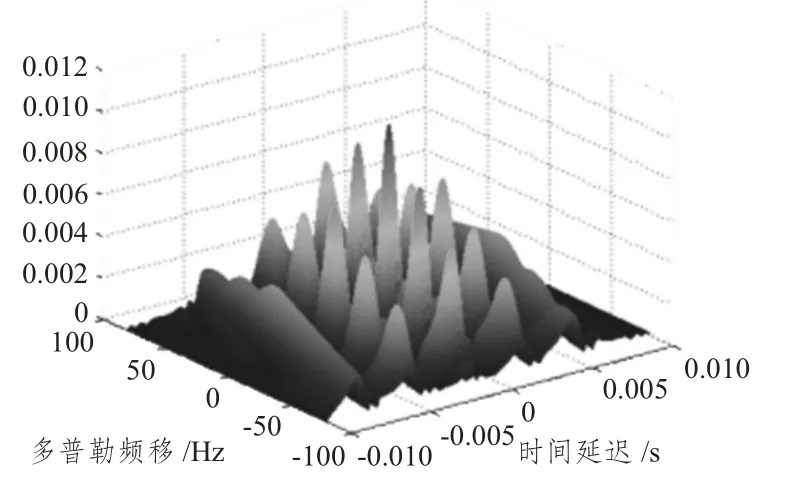
图2 PTFM 信号模糊函数Fig.2 Ambiguity function of PTFM signal

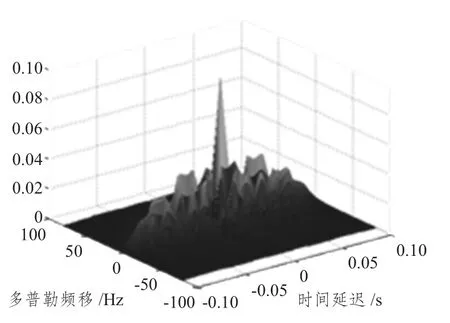
图3 LFM-Barker 码信号模糊函数Fig.3 Ambiguity function of LFM-Barker signal

信号的模糊度图为信号模糊图的最大值下降到0.707 (-3 dB)倍处的截面图，反映了信号对相邻目标频移(速度)与时延(距离)分辨的能力，也反映了目标距离、速度的测量精度。截面的大小说明了| χ(τ，ξ)| 曲面的陡峭程度，曲面越陡，则截面越小，相邻的目标越易分辨［2］。

图4 ～图6 给出SFM 信号/PTFM 信号模糊度图/LFM -Bark 码信号信号模糊图的最大值下降到0. 707 (- 3 dB)倍处的截面图，即模糊度图。

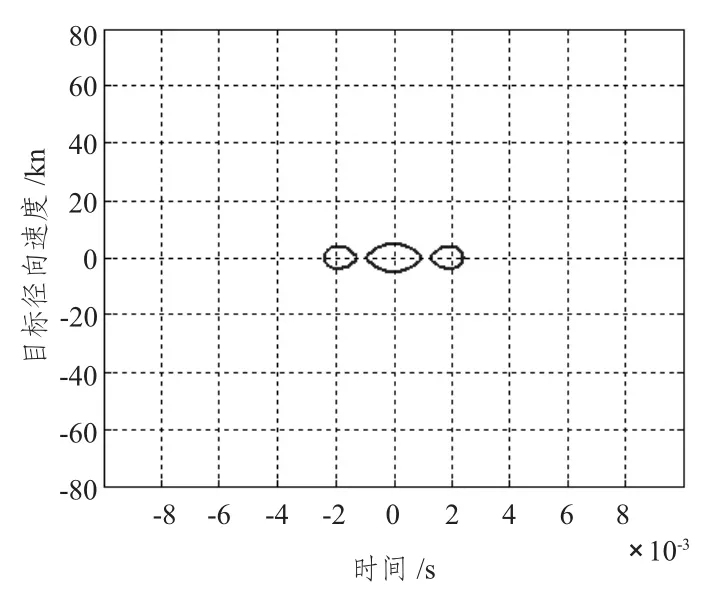
图4 SFM 信号对应截面图Fig.4 SFM signal′s cross-sectional view

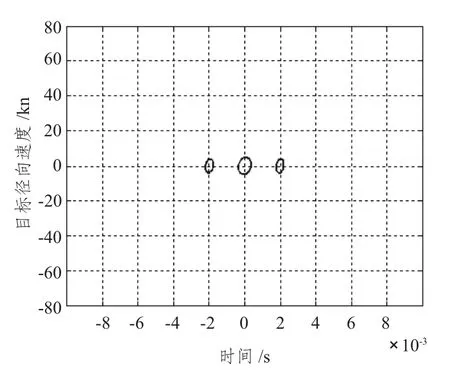
图5 PTFM 信号对应截面图Fig.5 PTFM signal′s cross-sectional view

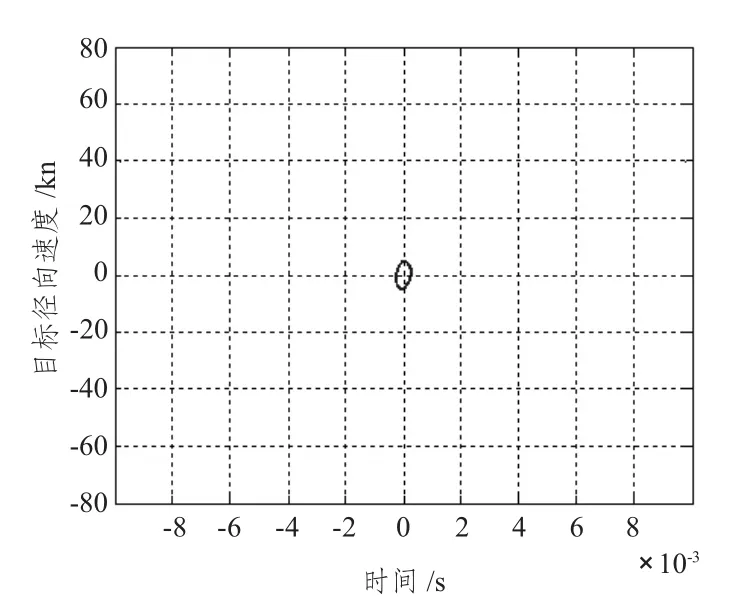
图6 LFM-Barke 码信号对应截面图Fig.6 LFM-Barke signal′s cross-sectional view

信号的时频分辨力如表1 所示。

表1 信号的时频分辨力Tab.1 Time-frequency resolution of signals

分析信号的模糊函数图与模糊度图得出:

单频矩形脉冲信号 (CW 信号)不能同时获得较高的时间分辨力和频率分辨力，两者不可兼得，提高其中一个的分辨力，另一个分辨力必然降低。

线性调频信号(LFM 信号)的时频分辨力可以单独调整，但是LFM 信号存在距离-速度二维耦合，当速度和距离均未知时，测量会带来附加误差。

正弦调频信号(SFM 信号)是一种由多个窄带信号组成的宽带信号。其信号具有钉板型的模糊度图，抗多普勒混响能力较强，但是测距能力较差，且多普勒旁瓣将使信号产生测速模糊。

调频脉冲串信号(PTFM 信号)为梳状谱信号，梳状谱信号的频谱由许多独立的谱线组成，信号能量如同宽带一样在频域分布，而其较窄的谱线如同单频信号一样具有多普勒敏感性。PTFM 信号有尺度-速度联合分辨能力，可用于强混响下的弱目标检测，缺点是需要进行距离-速度联合搜索，数据存储量大。且同正弦调频信号(SFM 信号)一样，其多普勒旁瓣将使信号产生测速模糊

线性调频-Barker 码信号LFM -Barker 码信号将LFM 信号和Barker 码信号复合形成的复合信号［9-10］，LFM 信号能实现较宽的带宽，多普勒容限大，但输出响应会产生一个附加时延，与多普勒频移成正比。Barker 码信号的模糊函数呈近似“图钉型”，有较高的时频分辨力，但当信号回波与匹配滤波器的多普勒频移失谐时，匹配滤波器起不到脉冲压缩作用，而且相位编码信号是多普勒敏感信号只有在目标的多普勒频率变化不大时性能良好。复合信号具有2 种信号形式各自的优点，具有较高的时间/频率分辨力以及较低的模糊旁瓣。

2 抗混响性能分析

2.1 Q 函数的定义

Q 函数［2］为发射信号模糊度函数的平方沿距离维的积分。其定义为

Q 函数可认为是在所有距离上的散射体产生的混响回波经过匹配滤波后输出能量的卷积，假设混响散射体静止，沿距离均匀分布且强度相等，则Q 函数表征了不同多普勒条件下匹配滤波器输出的混响强度，可用来比较不同发射波形的抗混响能力。

2.2 信号的Q 函数对比分析

CW，LFM. SFM，PTFM，LFM - Barker 码信号的Q 函数如图7 所示［11］。

图7 CW，LFM.SFM，PTFM，LFM-Barker 码信号的Q 函数对比图Fig.7 Q function comparison chart of CW，LFM.SFM，PTFM，LFM-Barker code signals

Q 函数可用来比较不同发射波形的抗混响能力，Q 函数值越小，表明输出的混响强度就越小，越有利于混响限制下目标的检测。从图7 中可以看出，在选定的参数条件下:

1)在探测零多普勒和低多普勒目标情况下(0 kn ～10 kn)，CW 信号的Q 函数最高，LFM 最低。相同带宽条件下，SFM 信号、PTFM 信号、LFM -Barker码信号、LFM 信号的Q 函数依次降低，抗混响性能依次更优。

2)在探测中等多普勒目标情况下(20 kn ～40 kn)，SFM 信号具有最低的Q 函数，PTFM 信号次低，说明梳状谱信号在此种情况下具有最优的混响抑制性能。

3)在探测高多普勒目标情况下(40 kn 以上)，可以看出CW 信号的Q 函数最低，具有最优的抗混响性能。

4)LFM - Barker 码信号集合了LFM 信号和Barker 码信号的优点，不仅具有较高的时间/频率分辨力以及较低的模糊旁瓣，而且对于低速目标具有较好的抗混响性能。低多普勒情况信号的混响抑制能力相对巴克码信号有明显大概2 dB 的改善，而相对于LFM 信号抗混响能力下降不大，约为0.5 dB。

3 结 语

本文利用模糊函数和Q 函数，对梳状谱信号(SFM 和PTFM 信号)以及在雷达中广泛研究但在声呐中鲜有研究的基于巴克码的LFM-Barker 码信号的时频分辨力、抗混响能力进行仿真研究，并与常规声呐信号(CW 和LFM 信号)进行对比分析，验证了梳状谱信号和基于巴克码的LFM -Barker 码信号具有更好的时频分辨性能，其中梳状谱信号在中等多普勒情况下抗混响性能最优，基于巴克码的LFM-Barker 码信号在低多普勒情况下抗混响性能优异，采集的湖试数据也佐证了上述分析的正确性，为主动声呐波形优选提供了参考和依据。

［1］田坦，刘国枝，孙大军.声呐技术［M］.哈尔滨工程大学出版社，2006.

［2］李启虎. 声呐信号处理引论［M］. 北京:海洋出版社，1985.

［3］李峻年，孟士超，佘亚军. 主动声呐发射波形设计研究［J］.舰船科学技术，2014，36(4):108 -113.LI Jun-nian，MENG Shi-chao，SHE Ya-jun. Design of the transmitted waveform of active sonar［J］.Ship Science and Technology，2014，36(4):108 -113.

［4］马国强，徐德民，王新晓.线性调频信号的抗混响起伏模型［J］.舰船科学技术，2004，26(1):42 -45.MA Guo-qiang，XU De-min，WANG Xin-xiao. Anti reverberation and fluctuation model of chirp signal［J］.Ship Science and Technology，2004，26(1):42 -45.

［5］梁国龙，张瑶，付进，等.新型主动声呐梳状谱信号设计［J］.哈尔滨工程大学学报，2012，33(3):302 -307.LIANG Guo-long，ZHANG Yao，FU Jin，et al.The design of new comb spectrum signal of active sonar［J］. Harbin Engineering University，2012，33(3):302 -307.

［6］陈韶华，张忠波，坟宏刚.主动声呐SFM 信号的抗混响性能分析［J］.声学技术，2011，30(3):268 -270.CHEN Shao-hua，ZHANG Zhong-bo，FEN Hong-gang. Anti reverberation performance analysis of SFM signal of active sonar［J］.Acoustic Technology，2011，30(3):268 -270.

［7］刘冲，方世良.主动声呐组合波形抗混响性能分析［J］.声学技术，2009，28(5):135 -136.LIU Chong， FANG Shi-liang. Anti reverberation performance analysis of active sonar of combined waveform［J］.Acoustic Technology，2009，28(5):135 -136.

［8］Henry C，Hung L.Geometric comb waveforms for reverberation suppression［J］. IEEE，1995.

［9］李永胜，吕林夏.LFM-costas 编码信号在水下目标识别中的应用［J］.舰船科学技术，2012，34(6):74 -78.LI Yong-sheng，LV Lin-xia.LFM-costas coded signals used in underwater target recognition［J］. Ship Science and Technology，2012，34(6):74 -78.

［10］PECKNOLD S P，RENAUD W M，et al. Improved active sonar performance using costas waveforms［J］. Journal of Oceanic Engineering，2009，34(4):559 -574.

［11］刘贯领，沈文苗，凌国民.声呐信号抗混响能力和声兼容性分析［J］.声学技术，2008，27(3):319 -322.LIU Guan-ling，SHEN Wen-miao，LING Guo-min. Analysis of anti-reverberation capability and compatibility of sonar signals［J］.Technical Acoustic，2008，27(3):319 -322.