基于双种群混合遗传算法的车辆调度问题研究

胡云清 （山西交通职业技术学院，山西 太原030031）

HU Yun-qing (Shanxi Traffic Vocational and Technical College, Taiyuan 030031, China)

0 引 言

物流活动作为企业的“第三方利润源泉”，在提高企业经济效益、降低企业成本等方面发挥着重要作用。而车辆路径优化作为企业物流活动的关键，更是广受学者们的关注[1]。特别是在配送成本较高、严重影响企业生存发展和城市交通拥堵越来越严重的情况下，通过对企业车辆配送路径的优化，降低企业配送成本、缓解城市交通拥堵，更是意义重大。

分析现有相关文献可知，车辆路径优化问题的求解算法可以分为精确算法和近似算法。精确算法指能够求出全局最优解的算法，而近似求解算法则无法求出问题最优解、只能求得最优解的近似值[2]。由于精确算法的计算量会随着问题规模的增大而呈指数增长，所以它在实际问题中应用较为有限。相比之下，对于近似算法的研究更为广泛。其中遗传算法由于具有搜索空间较大、求解精度较高等优点，更是倍受学者的青睐。如文献[3-5]均对车辆路径问题的遗传算法进行了研究。但传统遗传算法也存在着容易陷入局部最优解、收敛速度较慢等问题，影响着算法的求解性能。对此，本文对传统遗传算法进行了改进，提出了求解车辆路径优化问题的双种群混合遗传算法。

1 车辆路径优化问题模型

车辆路径优化问题一般可以描述为：企业配送中心需要用多辆车辆完成不同客户点的需求配送任务。配送中心位置已知，客户点需求量和位置信息已知，每辆车的载重量一定，且具有载重约束，即车辆所载货物不能超过车辆最大载重量，要求合理规划车辆行驶路径，使车辆总行驶距离最短，同时必须满足如下几个条件：（1） 企业车辆足够多，能够完成企业配送任务，且车辆类型相同；（2） 每个客户的需求量均不超过车辆的最大载重量；（3） 必须满足所有客户的需求，并且一个客户只能由一辆车服务。

设需要服务的客户数量为K，完成此次配送任务所需要的车辆数为m；企业配送中心用0 表示，各客户点用表示；每个客户的需求量为车辆的最大载重量为q，且gi ＜q；dij表示客户i到j的距离。定义模型决策变量如下：

则车辆路径优化问题的数学模型为：

其中，式（1） 表示车辆总行驶距离最短的优化目标。式（2） 为车辆载重约束，即车辆不能超载。式（3） 有两层意义，首先表示每个需求点只能由一台车进行配送服务；其次表示所有车辆从配送中心出发，且完成配送任务后必须返回配送中心。式（4） 和式（5） 表示两决策变量之间的关系。式（6） 和式（7） 表示0-1 变量约束。

2 双种群混合遗传算法

遗传算法局部寻优能力较强，而且并发性较好。但同人的进化一样，随着算法的进行，种群中的个体逐渐靠近最优解，其特性逐渐稳定，种群达到了一种平衡状态。此时种群的特性基本不再变化。因此在传统遗传算法后期，算法往往容易陷入局部最优解。本文提出的双种群混合遗传算法正是针对这种情况，在算法中同时使用两个种群进行优化，并且在每一次迭代结束后，都将由两个种群中选出的小种群进行互换，进而不断打破种群的平衡，跳出局部最优解，提高算法求解性能。双种群混合遗传算法具体的操作为：第一步，建立两个规模相同的种群。第二步，以不同的交叉概率和变异概率分别独自进行交叉和变异操作。第三步，在每一次迭代完后，从两个种群中分别取出由各自最优个体与一定数量的随机个体组成的小种群，将各自的小种群进行交换，进入对方种群中。同时，为了提高算法的求解速度，本文还利用2-opt 算子将种群中的最优个体进行了进一步优化。

双种群混合遗传算法中，每个种群都是按相同的方式进行选择、交叉和变异等遗传操作，因此如下的相关介绍均是针对两个种群同时进行的。

2.1 编码策略。 参照文献[3]，采用自然数串编码机制将每条配送路径编制成长度为K +m+1 的横向量（0,i1,i2,…,ie,0,if,…,ik,0,…,0,ip,…,iq,0 ），其中0 为配送中心，ik表示序号为ik的客户。

2.2 初始种群生成。在初始种群生成算法上，首先随机产生n个客户的全排列；然后，在全排列首尾添加0；最后，将m-1 个0 随机插入到全排列中，但两个0 不能相邻。

2.3 适应度函数选取。一般情况下，个体适应度值越高，表示个体越优秀，解的质量越高。所以本文对式（1） 进行如下改进，作为遗传算法的适应度函数。

式中，b为常数，根据车辆路径优化问题的规模而设定。

2.4 遗传算子。遗传算法的遗传算子包括选择算子、交叉算子和变异算子。在选择算子上，本文采用轮盘赌算子选取优秀个体；交叉算子和变异算子均采用传统遗传算法的相应算子，由于现有文献多有阐述，再此就不再一一介绍。

2.5 种群交叉。随机从种群A 中选取num个个体（num的值根据具体问题设定） 和最优个体，同时也从种群B 中选取num个随机个体和最优个体。将两个种群对应的num+1 个染色体进行互换，进入对方种群中。同时，由于在算法进化过程中，种群中的优秀个体往往存在交叉点，这不仅降低了算法的收敛速度，同时还影响了算法的全局寻优能力。为了加快算法收敛速度、提高算法全局优化能力，采用文献[6]中的2-opt 算子消除最优个体的交叉点，提高优秀个体的质量。具体操作如下：

随机选精英个体中的两条边，记为（i,j）和（i+1,j+1 ），将其拆分后重新连接起来组成新的路径（i,i+ 1 ）和（j,j+ 1 ），如果更新后的路径满足车辆载重约束，且使目标函数更小，则说明该交叉点可以消除，执行上述操作。重复上述操作，直到所有交叉点消除完为止。

3 算例分析

采用有能力约束的车辆调度问题的标准算例进行仿真实验①。为了验证算法的求解性能，分别利用传统遗传算法（GA）、禁忌搜索算法（TS） 和本文算法对算例进行求解，并对求解结果进行了统计，结果如表1 所示。

从表1 中可知，在问题规模较小时，三个算法都具有较高的求解精度，但GA 算法和本文算法求解精度更高。而随着问题规模的逐渐增大，GA 算法和TS 算法明显陷入局部最优解，本文算法在求解精度上虽然有所下降，但仍然能够取得较好的求解结果。说明通过对传统遗传算法的改进，本文算法在全局优化能力上有所提高，优于GA 算法和TS 算法。这是由于通过两个种群之间的交叉，使种群始终保持着多样性，进而提高了算法的全局寻优能力。

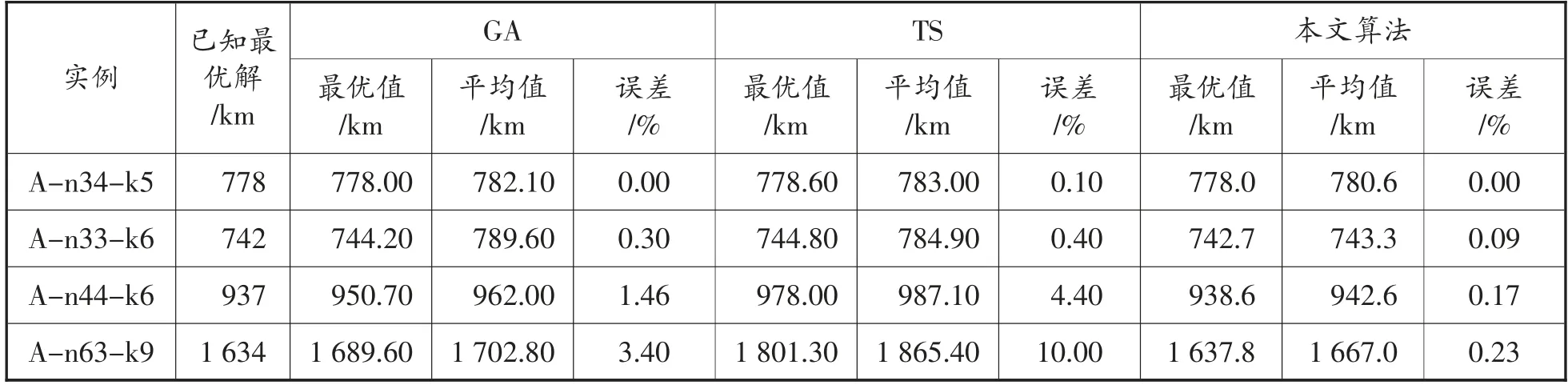
表1 标准算例测试结果

4 结束语

车辆路径优化问题有利降低企业配送成本，促进企业的发展。针对传统遗传算法存在的诸如容易陷入局部最优解等问题，本文提出了求解车辆路径优化问题的双种群混合遗传算法，为车辆路径问题的求解提供了新的研究思路。当然，本文仍然存在一些不足的地方，有待进一步改进，如：本文假设企业拥有的车辆类型相同，这与企业配送的实际情况具有一定的差距，论文的下一步研究方向即为考虑多车型的车辆路径优化问题。

注：①数据来源于：http://ftp.ics.uci.edu/pub/machine-learning-databases/。

[1] 许茂增，余国印. 城市配送研究的新进展[J]. 中国流通经济，2014(11):29-36.

[2] 李娟，余国印. 综合成本最小的车辆调度问题及混沌萤火虫优化算法[J]. 物流技术，2015(7):180-183.

[3] 许茂增，余国印，周翔,等. 综合成本最小的低碳车辆调度问题及算法[J]. 计算机集成制造系统，2015(1):26.

[4] 杨渝华，李敏. 基于改进遗传算法的成品油配送车辆调度问题研究[J]. 物流科技，2015(1):148-153.

[5] 王永，杨晓洁，胥冬川,等. 基于禁忌遗传算法的邮政运输车辆调度问题[J]. 系统工程，2014(8):102-109.

[6] BIANCHI L, KNOWLES J, BOWLER J. Local search for the probabilistic traveling salesman problem: correction to the 2-ppt and 1-shift algorithms[J]. European Journal of Operational Research, 2005,162(1):206-219.