飞机缺件停飞与出动能力关系研究

段 刚，刘臣宇，俞金松 （海军航空工程学院，山东 青岛266041）

DUAN Gang, LIU Chen-yu, YU Jin-song (Naval Aeronautical Engineering Institute, Qingdao 266041, China)

0 引 言

按照惯例，飞机缺件停飞率通常用来衡量航材保障的效能。但缺件停飞率作为衡量供应保障效率的管理指标其有效性已日益引起人们的研究兴趣。有观点认为，缺件停飞率高，飞机出动能力就低，两者之间存在一种线性负相关的关系。据此就可以将飞机的缺件停飞率作为衡量飞机出动能力的一项重要指标。这是一种没有进行定量分析的结论，不具备科学性。在航材不到位的情况下，机务人员通过串件拼修，可以保证飞机的出动能力不受影响。因此，定量分析缺件停飞与出动能力的关系有一定的研究和应用价值。如果能在缺件停飞与飞机出动能力之间建立某种关系的话，则在评估飞行单位完成其所分配任务的能力时，缺件停飞率应是有用的工具。缺件停飞率与出动能力之间任一关系的存在是选用适当的统计方法检验的。为了衡量缺件停飞率对飞机出动能力的影响，采用统计的因缺件停飞而取消的飞行任务数据，并以此作为衡量影响飞行的最佳方法。在其它所有因素保持不变的情况下，衡量缺件停飞率对飞机出动能力的影响程度，其唯一正确的指标是计算确定因缺件停飞的情况取消了多少次飞行任务。

1 缺件停飞率

当一架飞机因缺少备件而不能完成飞行计划中的任何一项时，该机就属于缺件停飞。一个机种的缺件停飞率定义为，在规定的期限内累计的缺件停飞时数除以同期内飞机占有的总时数，这一比值就是缺件停飞率。如某机场全月停放s架J型机，则一月份占用总时数z=s（）J×31×24，期间a架J型机缺件停飞n天，本月中s架J型机缺件停飞时数q=a×n×24。因此，一月份缺件停飞率为an/31s。

影响缺件停飞率的因素有：机场修理能力；库存量管理；串件拼修规定；飞行计划的重要性；飞机的寿命；对申请器材的积极供应；缺件停飞报告的缺陷；送修器材待收修复品的管理；备件供应与维修部门协作配合；调用紧急配套器材等。

现实中单纯以缺件停飞率这一指标，去衡量航材保障效果是不准确的。因此，一个机场某一缺件停飞率，可能不等于另一机场同一缺件停飞率。但若在缺件停飞率与飞机出动能力之间建立某种关系，则在评估一个机场完成飞行任务的能力时，缺件停飞率可作为可靠参数。初步分析认为，在其他因素保持不变的条件下，衡量缺件停飞率对飞机出动能力的影响程度，其唯一正确的指标是计算确定因缺件停飞的情况取消了多少次飞行任务。

2 模型分析

选定的各机场缺件停飞率分别与各自的同期缺件取消飞行任务率相比较，并分析有何关系。同时，各个机型的缺件停飞率分别与各自的缺件取消飞行任务率相比较，以确定在整个机型内它们是否存在一种关系。利用散点图可便于识别模型，如线性模型、双曲线形、幂函数模型、指数型等，简化了选择合适回归模型的工作。实例如下：该例的数据（如表1 所示） 显示了一种线性关系，再辅以相关分析和回归分析。设定数据散点图如图1 所示。

表1 设定数据（某机场某型飞机）

挑选回归模型方程：

线性方程：Y=A+Bx

二次方程：Y=A+Bx2

为了确信在问题变量之间存在强的线性关系挑选r2=0.8 作为相关重要性的衡量指标。若r2大于或等于0.8，管理人员就能运用缺件停飞率十分准确地预测取消飞行任务数。任何小于0.8 的r2值预测取消任务数就没有多大价值。在这种情况下，用其他预测方法，如果取平均值，可能得出更好的结果。

3 引入数据

线性模型检验数据结果：线性模型r2=1，非线性模型r2=0.9398；非线性模型检验数据结果：线性模型r2=0.9404，非线性模型r2=1。

表2～表5 按不同情况整理，提出相关系数平方值汇总情况。

表2 不同机场两种机型的r2

从表2～表5 看出，无论怎样分类进行分析，所有r2值都明显低于所指定的指标值0.8。

4 数据分析

第一个分析结果是，当所有其他因素不变时，缺件停飞率与飞机出动能力之间不是密切相关的。飞机缺件停飞率增加或减小一个量，不会独自对飞机出动能力造成有利或不利的影响。

第二个分析结果是，对各类机种进行比较，可以看出相应的缺件停飞率与缺件取消飞行任务率的关系是有很大区别的。由此可以推断一种可能性，即：单一考虑确实存在一定的相关性，但只有将机种作为整体考虑时这种关系才显得稍微密切。

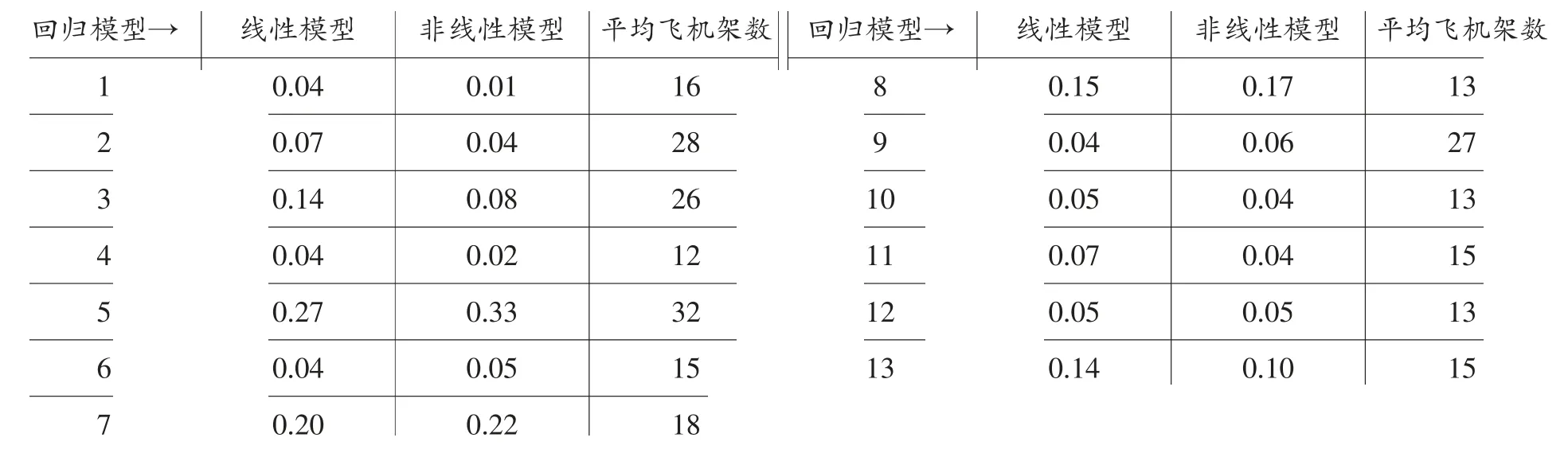
表3 不同机场某种机型的r2

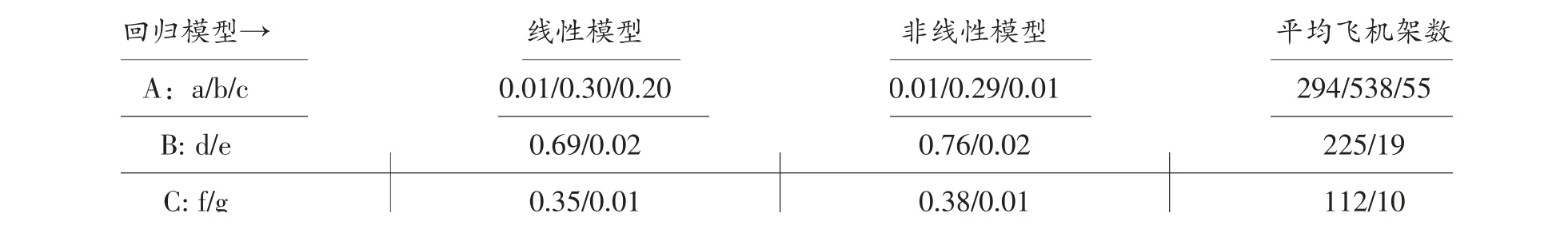
表4 按机场和机种的r2

表5 飞机平均架数的r2

第三个分析结果是，当所研究的飞机数量变化时，用缺件停飞率预测飞机出动能力，效果不好。由此断定缺件停飞率与飞机出动能力之间的关系不受装备飞机数量的影响。

根据分析结果，第一条建议是，将数据资料扩展到更长的时间范围，这样才能完成缺件停飞率与缺件取消飞行任务相关性的分析。由于本文引用数据涉及时间范围相对较短，因此回归方程受到散点图中少数极端点数据的影响。例如，18 个月中一极端数据点有可能使r2从一个重要值（r2≥0.8 ）降低到非重要值（r2≤0.8 ）。为了减轻这种影响，研究表明，3 年的数据就能减弱极端数据点可能出现的影响，并会提供比较准确的结果。

第二条建议，研究中可将串件拼修率和常用器材寿命考虑在内，这两个变量是影响飞机出动能力的潜在因素。例如，运用关于三个变量的多元线性回归的标准方法，计算每一个相关的强度和趋势，然后检验各个变量，求出最佳影响因素。研究有助于揭示上述变量的关系，并可清除有关测量值的许多相互矛盾的观点。

5 结 论

总之，利用缺件停飞率和缺件取消飞行任务率这两个变量进行线性回归分析，相关系数r2低于0.8，这表明缺件停飞率和缺件取消飞行任务率之间存在弱相关性。因此，在未更好地研究出两者之间的实质性关系之前，都不要盲目地把一特定的缺件停飞率与某一具体的飞机出动能力联系起来。进一步考虑，缺件停飞率作为衡量供应保障率的管理指标应当进行改进，针对不同的机种，重新制定相应的缺件停飞标准。在新的动态缺件停飞保障概念中，可以考虑将机种的寿命、飞行任务的性质和分散形式综合形成一个数字保障目标，该目标将是新的缺件停飞标准。

[1] 刘臣宇,等. 航材供应[M]. 北京：国防工业出版社，2009:30-31.

[2] 左召军，钟新辉. 航材消耗的时间序列分析[J]. 长沙航空职业技术学院学报，2004(3):29-32.

[3] 于倩，干晓蓉. 灰色多元线性回归分析[J]. 云南师范大学学报，2009,29(3):19-22.

[4] 丁士俊，姜卫平，杨颜梅. 整体最小二乘线性回归模型与算法[J]. 测绘通报，2012(12):8-10.

[5] 鲁铁定，陶本藻. 基于整体最小二乘法的线性回归建模和解法[J]. 武汉大学学报（信息科学版），2008,33(5):504-507.

[6] 张志勇，文桂林. 时变时滞系统的灰色预测非线性PID 控制[J]. 系统仿真学报，2009,31(5):44-46.