一种改进型蚁群算法在带硬时间窗的战场车辆路径问题中的应用研究

吕 游，杨 波 LV You, YANG Bo

（国防科学技术大学 指挥军官基础教育学院，湖南 长沙410072）

(College of Basic Education for Commanding Officers, National University of Defense Technology, Changsha 410072, China)

“兵马未动，粮草先行”，后勤补给在战争中具有不可替代的作用，随着战争形态、战争规模和作战方式的不断演变，“深挖洞、广积粮”的预有准备的大量囤积已经不能满足现代战争中作战部队对后勤补给物资的需求，实时、快速、准确的“精确保障”也就应运而生。军事物流是后勤补给的重要环节，车辆配送则是确保补给物资及时、准确、高效运送到作战单元的关键一环。

1 带时间窗的战场车辆路径问题简述

带时间窗的车辆路径问题（Vehicle Routing Problem with Time Windows，VRPTW） 也被称为车辆配送问题。设某一局部战场只有一个物资配送中心，该配送中心对多个作战单元进行服务保障，有多台型号相同的运输车辆可供调用，多辆运输车可以同时从配送中心出发，各自按照一定次序完成对不同作战单元的服务保障。各配送车辆型号、容量（最大载重量）、平均行驶速度均相同，各作战单元只在一定时间窗口内接受服务，若配送车辆早于规定服务时间到达作战单元则选择等待，直至规定时间方可开始进行服务，若配送车辆晚于规定时间到达则作战单元拒绝接受服务，一个作战单元只能被一辆车服务。各作战单元有相应的服务时间和物资需求量，在完成对某一作战单元的服务后，配送车辆可以选择下一个作战单元，也可以回到配送中心，配送中心及各作战单元间的距离预先可知，目标函数为配送车辆总路程。

2 VRPTW 的数学模型

Q：配送车辆的容量（最大载重），本文假设配送车辆为同种型号，各运输车量容量均相同；

qi：第i个作战单元的物资需求量，其中i=1,2,…,n；

dij：从出发点i到目标点j的车辆行驶距离，其中i,j=0,1,2,…,n；

tij：配送车辆由出发点i至目标点j的行驶时间，其中i,j=0,1,2,…,n；

ti：配送车辆为作战单元i提供服务所需要的时间（卸货时间），其中i=1,2,…,n；

Li：车辆实际经过的路线，其中i=1,2,…,2n，一般情况下车辆实际经过路线的作战单元数量小于2n；第i个作战单元接受服务的最早时间；第i个作战单元接受服务的最晚时间；

xkij：车辆k的行驶线路是否包含由点i出发直接到点j的路段，其中：i,j=0,1,2,…,n，k=1,2,…,m；

yki：车辆k是否为作战单元i提供服务，其中i=1,2,…,n，k=1,2,…,m；

问题的基本模型为：

在上述模型中，式（1） 为目标函数，表示配送总路线最短，即总费用最小；式（2） 表示每辆车所担负的服务任务的作战单元的总需求量不大于车辆最大载重量；式（3） 表示任何一个作战单元只能由一辆车对其进行服务；式（4）、（5） 表示任何配送车辆都是从配送中心出发，并只能选择一个作战单元进行配送；式（6） 表示每辆车最后回到配送中心；式（7） 表示若某一车辆到达作战单元j则必须为该作战单元服务；式（8） 表示任一配送车辆对任一作战单元可能选择服务或者不服务；式（9） 表示每个作战单元接受服务的时间窗口；式（10） 表示车辆k为作战单元i的服务的时间段；式（11）、（12） 表示配送车辆k为作战单元Li完成服务后，若对下一个作战单元Li+1进行服务，则到达该作战单元的时间必须在该作战单元所要求的时间窗之内；式（13）、（14） 表示配送车辆k为某作战单元Li+1服务的时间段与该作战单元所需的服务时间tLi+1的关系；式（15）、（16） 表示相应变量的取值范围。

3 VRPTW 的改进型蚁群算法

常见的求解VRP 问题有禁忌搜索算法、模拟退火算法、遗传算法及蚁群算法等。VRP 问题已经被证明为NP-hard 问题，很难通过传统算法得到其最优解。本文根据VRPTW 的特点，设计了一种改进蚁群算法对问题求解。蚁群算法在求解该问题中通过个体之间的信息传递，有利于在发现有效解，同时蚁群算法通过对信息素的反馈机制对有效解不断增强，使得问题不断趋近于全局最优。当然，蚁群算法也存在一定缺陷，如搜索时间较长，构造有效解需要大量计算时间，容易出现局部停滞现象等。本文主要在两个方面对传统蚁群算法进行了改进：一是将已访问点附近一定范围内符合访问要求的点作为待访问对象，这样有利于减少搜索时间和计算量，带来的问题在于可能会错过最优解，避免错过最优解的方法为合理设置并变化待访问点数量；二是用局部线路车辆访问过的作战单元数量和该路线长度作为信息素更新的依据，以突出车辆利用率。

3.1 改进的蚁群算法基本流程

Step1 初始化每个参数，假设有m 只蚂蚁从配送中心出发，分别选择一个作战单元作为第一个访问点。

Step2 对每个蚂蚁列出全部未访问点，设其个数为S1个。

Step3 判断S1取值。若S1=0，该蚂蚁已经完成全部配送任务，选取下一访问点为配送中心，本条线路配送结束。若S1＞0，从S1个未访问点中筛选出符合访问条件的未访问点为个，若S2=0，则表示没有可选点符合条件，车辆返回配送中心，若S2＞0，在以当前访问点一定距离范围内选取S=min（S,S2）个候选访问点，并将配送中心加入到候选访问点，按照一定概率选取一个点作为下一个服务点，返回Step2。

Step4 判断是否所有蚂蚁都已经完成配送任务。若所有蚂蚁都完成了配送任务，计算本次配送中各蚂蚁所经过的总路线长度，从中选出最短路线并记录，则按照一定规则更新信息素。

3.2 待访问点选择和信息素更新

待访问点的选择问题是影响VRPTW 计算复杂性的一个重要因素，我们希望在能够减少计算量的同时不遗漏最优解或者可行解。本文采取的策略是首先判断可选点的集合，在带时间窗的车辆配送问题中，配送车辆到达某一服务单元后，受到各种约束条件的限制，车辆可供选择的服务点的数量不断减少，进行可选服务点的筛查有助于减少不必要的计算。

信息素的更新是决定算法收敛速度和求解效率的关键环节，本文采取“指数分段更新”策略，较好地解决了信息素更新的问题。基本思想是将配送车辆（蚂蚁） 所经过的路径按照是否回到配送中心进行分段。该方法有利于快速区分不同路线的优劣程度，很大程度上提高了算法效率，同时为避免陷入局部最优，给定信息素最小值，确保更多路线能够被尝试。信息素具体更新方式如下：

用τij表示路线从i到j上的信息素，初始值设为单位矩阵；用ηij表示路线从i到j上的启发式信息值，初始值设为1/d表示对第k辆车在作战单元i可选择的目标点，pk（i,j）表示第k辆车在作战单元i选择作战单元j为配送目标的概率，Rk表示第k辆车所经过的路线。

式（17） 为第k辆配送车辆从作战单元i出发，分别以不同的作战单元j为目标点的概率，其中α 为残留信息的相对重要程度，β 为预见值的相对重要程度，本文仿真算例中令α=1，β=1；式（18）、（19）、（20） 表示信息素的更新步骤，其中式（18） 中K表示第k辆车所完成配送任务回到配送中心过程中所到达的作战单元的个数，λ 为指数因子，根据情况由人为给出，本文在仿真计算中令λ=3，取得了较好的计算效果，ρ 为信息素挥发参数，本文仿真计算中令ρ=0.5。τ0为信息素修正因子，由人为给出，以增加不同路线的选择概率，避免算法早熟，本文仿真实例中令τ0=0.1。

3.3 仿真计算示例

客户数为8 的VRPTW 问题，描述如下：某战场配送任务中，有1 个配送中心和8 个作战单元，各作战单元的需求量为gi（单位：吨），服务（或卸货） 时间为Ti（单位：小时），各作战单元的服务时间范围最大允许车辆数为5，车辆平均行驶速度为50，载重量为8。并且认为行驶时间与距离成正比，配送中心与配送点的距离由表2 给出。要求合理安排车辆的行驶路线，使得既满足条件完成运输任务，又能使总的花费最小。具体信息如表1。

[1]设置群体规模为60，进化代数为100，在赛扬双核T1400（主频1.73GHZ） 计算机上运行1 000 次，其得到最优解、得到最优解的概率、得到最优解的平均运行时间和平均迭代次数如表3、表4。

采用本文算法，使用因特尔酷睿2 双核E7500（主频2.93GHZ），比参考文献[1]中所用计算机处理器运算速度的1.7 倍。蚂蚁数量40、α=1.0、β=2.0、ρ=0.2，得到的最优结果与参考文献[1]中的结果相同，计算时间和迭代次数显著小于该文献中所用方法，基本情况如表5。

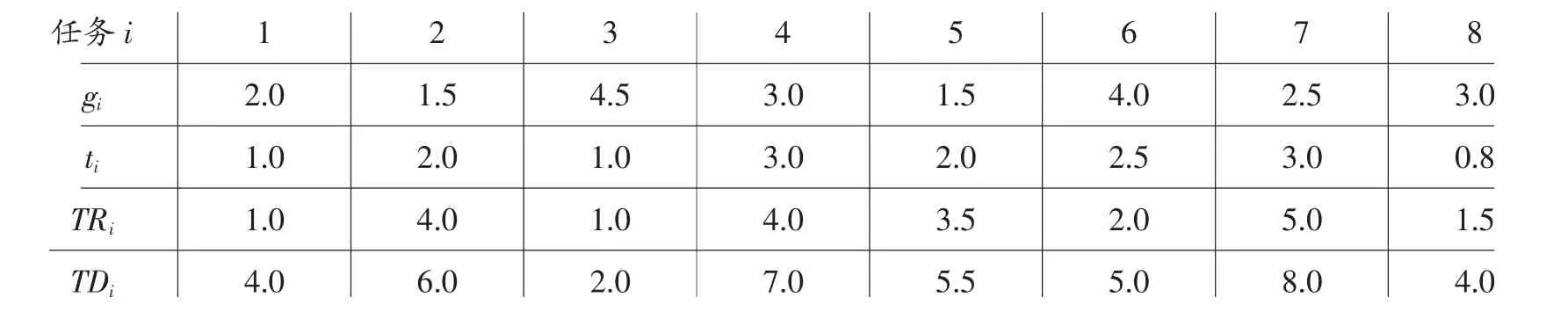
表1 客户数位8 的车辆配送问题描述

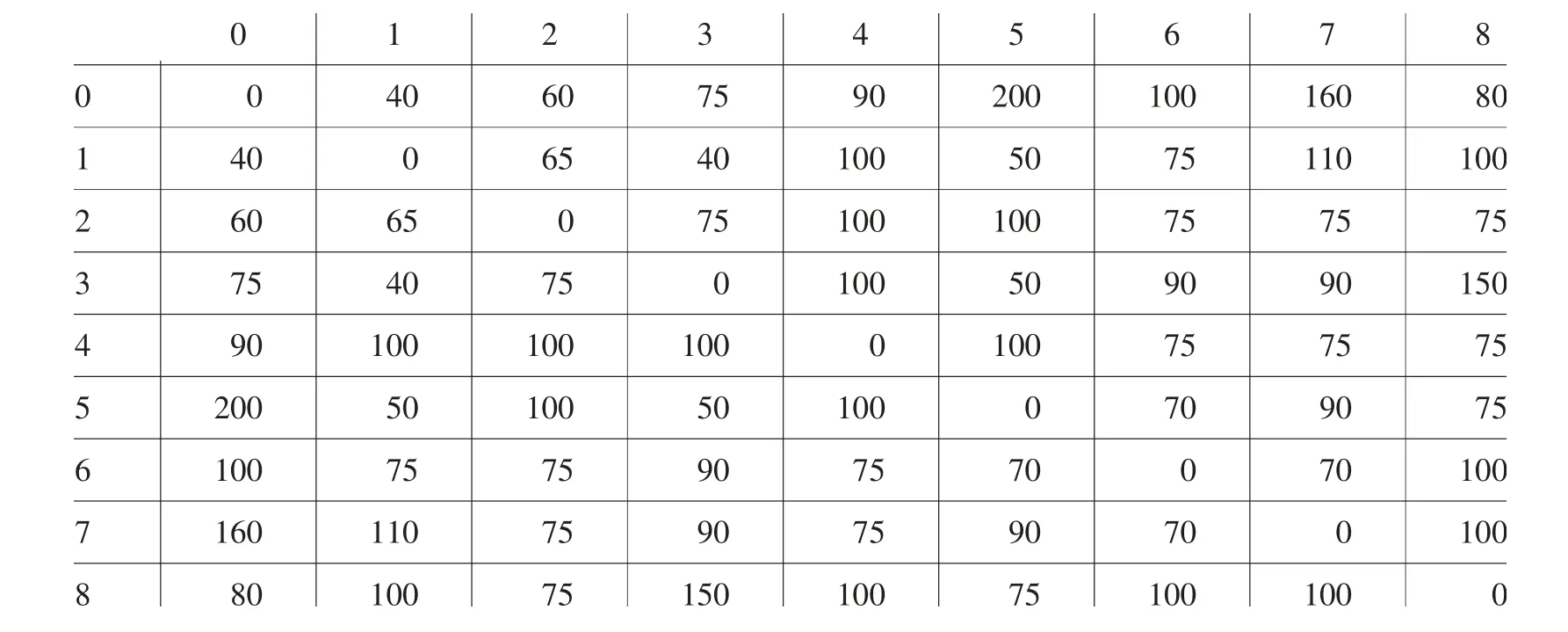
表2 各个作战单元（包括配送中心） 之间的位置关系

表3 参考文献[1]中的计算结果

表4 参考文献[1]中算法的计算效率

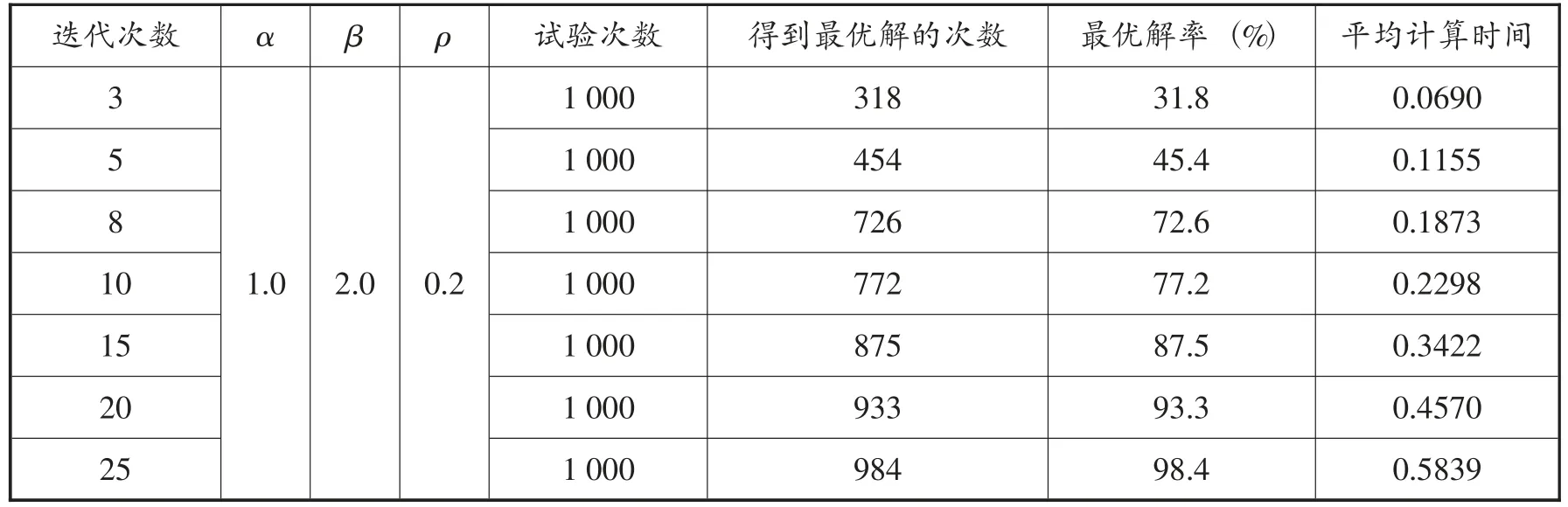
表5 本文算法的计算效率

4 结 论

本文在不使用局部搜索算法的情况下，通过改进蚂蚁选择路径过程中的关键问题——信息素的更新方式，提高了状态转移效率和信息素更新速度，有效避免了算法限于早熟。通过与同类文献结果对比，验证了改进的蚁群算法的有效性。

参考文献：

[1] 周和平. 军事物流配送路径优化问题研究[D]. 合肥：合肥工业大学（硕士学位论文），2009.

[2] 王宗喜. 军事物流概论[M]. 北京：海潮出版社，1993.

[3] 段海滨. 蚁群算法原理及其应用[M]. 北京：科学出版社，2006.