改进遗传算法在ETV 调度优化中的应用研究

郭春晖 （兰州交通大学 机电技术研究所，甘肃 兰州730070）

GUO Chun-hui (Institute of Electrical and Mechanical Technology, Lanzhou Jiaotong University, Lanzhou 730070, China)

0 引 言

图1 为大型货运站集装货物立体库的平面布置示意图，它由以下四大部分组成：（1） ULD 辊道式立体货架，是ULD 货物的存放单元。 （2） 升降式转运车（ETV），在货位之间的地面轨道上行走，实现货架上货物的存入或取出。（3） 集装货物分解组合系统与直通转运系统设备，用于集装货物的分解、组合等任务。（4） 管理控制中心，负责整个货运站的信息数据处理、监控终端、相关电气控制设备的运行[1]。

ETV 在地面轨道上穿梭，完成集装货物的出、入库任务。操作员或管理中心将取、送货的信息发送给ETV 的控制计算机，由计算机控制ETV 的运动。在任务量高峰时，如果ETV 执行存、取货任务过程中接收到新的任务指令，控制计算机会把新的命令加入到任务队列等待执行。但在实际的货运站内，尤其在任务密集的时间段，ETV 调度算法的优劣往往成为物流系统中的制约环节，所以针对ETV 的调度进行优化显得尤为关键。

1 ETV 运行的数学模型建立

选择ETV 的运动模型时，本文使用柔性S 型加减速度算法[2]。提出一种七段S 型加减速度算法，但该算法缺点是计算量大。五段S 型加减速算法与七段相比，省略匀加速和匀减速阶段，在保持速度平滑性的同时，大大降低了计算复杂度[3]。图2为五段S 型算法中速度V，加速度a，加速圆角参数j随时间的变化规律。T1为加加速和减加速时间；T2为匀速时间；T3为加减速和减减速时间。

根据加加速度、加速度、速度及位移间的动力学规律有:

进而可以得到：

每个货位长度为X，高度为Y。ETV 每完成一次调度操作要运行M列N层，则水平方向运行距离Sx=X*M，垂向运动距离为Sy=Y*N。

ETV 理参数如表1 所列：

表1 ETV 运行参数

集装立体货架采用纵向存储式，单个货位长为3.75m，共45 列；层高为3.75m，共5 层，货位数45*5*2=450。ETV 在水平运行时间和垂向运行时间分别为Tx,Ty：

那么ETV 在两个货位点之间运行的时间开销为：

通常，货运站货物处理区的任一批次的出入库都包含n个集装货物任务的操作，每个任务花费的时间主要由3 部分组成：（1） 两个货位点间负重行走时间Tτa；（2） 两个货位点间空载行走时间Tτb；（3） 每完成一次取/放货时间Tc，这部分的时间恒定。

由以上分析可知，完成1 个集装货物任务的操作的时间为：

2 遗传算法计算与求解

遗传算法以自然选择和遗传理论为基础，通过对生物在遗传和进化过程中选择、交叉、变异机理的模仿，来完成对问题最优解的自适应搜索的一种算法[4]。选择、交叉、变异运算是遗传算法的主要步骤，改进的遗传算法将针对这三个算子实现算法性能的提升。

2.1 选择编码策略

在研究调度优化问题时通常采用实数编码。因此在用改进的遗传算法对货运站调度进行优化时，首先要建立货位号和货位编码的对照表。

本文中的集装货物存储区有2 行、5 层、45 列。假设货位处于第2 行、第3 层、第3 列，则货位号用（2-3-3） 表示，对应编码号为28。具体编码方式参照表2。

2.2 定义适应度函数

将目标函数进行变换可得到适应度函数，依据目标函数要遍历所有等待任务的货位点而费时最短原则，目标函数可定义为：

由于在货运站内，等待任务列队是即时变化的，故每加入一个新的调度任务后需执行一次新的优化，会使个别任务等待时间太长。因此，考虑任务等待时间的因素，目标函数变为：

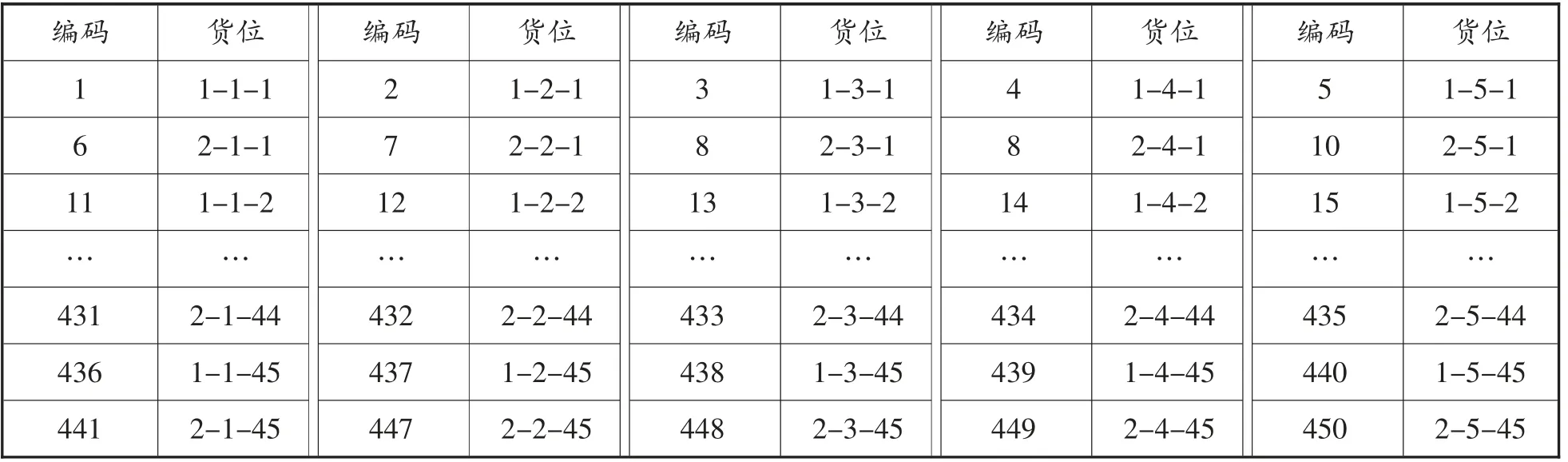
表2 编码号与货位号对照表

式中：ti表示任务等待的时间；β 表示根据工作模式使用的参数。

2.3 遗传算法的三个算子的改进

2.3.1 基于序的选择算子设计

适应度值是进行选择过程的依据。为了加快算法的收敛速度，本文采取的方法是快速选中种群中的优秀个体，并使优秀个体马上参与到下一代交叉运算。通过增大优劣个体间的适应度值，可将优秀个体快速选出。为了增大个体之间适应度值的区分度，通过基于序的评价函数来实现。首先对种群中的个体按花费总时间的长短排序，并据此确定个体在队列中的序号，对总时间越少的个体赋予小的序号数。如耗费最少时间的个体被赋予序号数1，则耗费最长时间的个体序号数为n，然后用下面的基于序的指数评价函数计算适应度：

式中，base为取值范围在0 到1 间的基数，μ 是个体通过排序后得到的序号数，由于评价函数经指数计算后得到数据值较小，乘以10 000 的目的是放大数据从而使其不会在计算中被舍去。例如，个体A序号数是5，个体B序号数是7，个体C序号数是2，选择基数为0.5，个体A、B、C的适应度分别为：

显然，通过该评价函数计算后C的适应度是A的8 倍，是B的32 倍，个体C的优越性变得更加突出，它被选作父代的可能性就大为提升。确保适应度最高的基因快速传到下代，加速算法收敛速度。

2.3.2 基于普莱姆算法的交叉算子设计

在用遗传算法求解货运站的调度优化问题时，货运站内每个货位点的位置编码采用实数编码，经常用到的交叉算子有：部分匹配交叉算子，顺序交叉算子，循环交叉算子等，上述交叉算子只是单纯产生新个体，在设计时没有充分结合问题本身的特性进行考虑，最终算法寻优效果在整体性能方面不理想。在货运站内，规定ETV 的起始点货位为1，最后执行完任务后要回到起始货位点，则把每个出入库任务货位点连起来是完全图。把ETV 从上一货位点到下一货位点运行所需的时间称为权，则要使ETV 依次抵达n个货位点，至少需要n-1 条边来表示，n个货位点和n-1 条边可生成一棵树，把n-1 条边的权值求和后存在一颗和最小的树，称这样的树为最小代价树。设U表示n个货位点的集合，E表示n-1 条边的集合，那么普莱姆算法就是一种求最小代价树的算法。

用普莱姆算法生成最小代价树的例子如图3 所示。

最小代价树生成方法如下：

（1） 任意选一顶点A，令U=｛A｝，寻找A的相邻边使其权值最小，产生一条边（A,B），则将B添入U内，（A,B）添入E内，得到U=｛A,B｝,E=｛（A,B）｝；

（2） 在E外再寻找A、B的邻边使权值最小，得到边（A,C），再将C添入U内，并把（A,C）添入E内，此时U=｛A,B,C｝，E=｛（A,B）,（A,C）｝；

（3） 在E外搜索A、B、C的邻边使其权值最小，得到边（B,D），将D添入U内，同时（B,D）加到E中，此时U=｛A,B,C,D｝，E=｛（A,B）,（A,C）,（B,D）｝，到此U中包括了所有的顶点。求得E的最小权值和为6。

根据普莱姆算法生成最小代价树的思想，设计一种基于普莱姆算法的交叉算子步骤如下：

（1） 在种群中选取两个个体Pa、Pb 作为父代，随机产生一个货位点，并把这个货位点作为子代个体Ca首先到达的货位点；

（2） 搜索ri在Pa、Pb 优化顺序中右边的货位点rj1、rj2，比较con（ri,rj1）和con（ri,rj2）耗时的大小，如果con（ri,rj1）＞con（ri,rj2），则按照ri到rj2的顺序更快，进入（4）；

（3） 若con（ri,rj1）＜con（ri,rj2），则按照ri到rj1的顺序更快，就把rj1加入到ETV 下一访问顺序的货位点，同时删去Pa、Pb中ri的值，重新将ri赋值rj1，再进入（2） 开始下一步搜索，直到Pa、Pb 中剩下唯一的货位点；

（4） 将rj2看成ETV 下一访问的货位点，同时删去Pa、Pb 中ri的值，重新将ri赋值rj2，继续转入（2） 开始搜索，直到Pa、Pb 中只剩下最后一个货位点；

（5） 通过Pa、Pb 向右寻优搜索杂交产生子代个体Ca。同样对Pa、Pb 向左寻优搜索杂交产生子代个体Cb。

2.3.3 基于随机时间长度的变异算子设计

设计一种基于随机时间长度的变异算子，可增大种群多样性，同时减小破坏优良个体基因概率，方法如下：

（1） 任意产生货位点r1和r2，初始循环次数p=1；

（2） 计算调度队列中上述两个货位点间的货位点数q；

（4） 在r1和r2之间选取两个货位点ri、rj，替换ri、rj的次序，p=p+1；

（5） 若k＜m，则返回（4），否则跳出。

该交叉方法由初始的货物点r1,r2之间的货物点数量q确定需要随机交换的次数s。若q越大，进行的替换次数就越多，否则就越少。根据时间耗费长短控制变异的次数，可以在保存了优良个体的同时增加了种群多样性。长短控制变异的次数，可以在保存了优良个体的同时增加了种群多样性。数量q确定需要随机交换的次数s。若q越大，进行的替换次数就越多，否则就越少。根据时间耗费长短控制变异的次数，可以在保存了优良个体的同时增加了种群多样性。

3 仿真验证

为了测试改进的遗传算法的性能，对图1 所示的集装货物存储区进行仿真试验。实际中出入库作业主要集中于空侧区域，因此只讨论空侧区域的I/O 口。空侧区域入口总共7 个，位置编号为41，101，181，201，311，341，441；出口共计6 个，编号为71，151，261，291，391，421。

有30 个入库任务R1～R30，货位编码为：53、79、235、154、337、335、435、287、399、69、88、6、197、133、142、77、330、379、434、400、277、199、84、9、108、321、342、222、263、21。

30 个出库任务C1～C30，货位编号为：8、55、183、79、83、160、255、365、302、421、5、17、13、72、11、121、180、200、340、263、38、175、438、411、393、10、45、383、415、400。

将标准遗传算法和改进遗传算法分别应用于机场货运站的ETV 调度优化中，用MATLAB7.11 进行仿真实验。初始种群个体为30 个，代沟为0.9，杂交率为0.7，变异率为0.02，使用标准遗传算法和改进遗传算法分别进行500 次迭代。

为了更好地显示改进遗传算法的优越性，分别比较其与标准遗传算法的单次优化效果和进行多次优化后性能的提升，对比结果如图4 和图5 所示。

对试验数据对比分析得出：用标准的遗传算法进行优化在迭代400 代左右后可得到最优解5 600s，而改进的遗传算法在迭代300 次后就得到最优解5 200s，优化提升7.14%，计算时间大约缩短20%。在前100 次的迭代中，改进遗传算法的收敛速度明显快于标准遗传算法。同时，由图5 可看出，将改进的遗传算法与标准的遗传算法选用相同参数分别优化20 次，改进遗传算法每次优化的结果都维持在5 200 秒左右，变化很平稳，而用标准遗传算优化会出现较突出的波动，最严重时可达到2%。

4 结 论

本文使用柔性S 型运动曲线模型，保证了ETV 运动的平稳性，大大减少了运动过程中货物的冲击；运用组合优化的思想对标准遗传算法选择、交叉、变异三个算子进行改进并应用于ETV 的调度作业，相比标准的遗传算法具有更好的可收敛性，避免了标准遗传算法陷入局部最优解的缺陷，同时提高了优化效率，节约了计算时间。仿真结果证明，该算法对于提高ETV 的调度效率是有效的，提高货运站的服务质量，降低运行成本都有积极意义。在今后的研究中，可考虑当多台ETV 同时运行于一条轨道上的情况，从而使货运站的吞吐量效率更高。

[1] 邱建东. 大型机场货运站核心物流装备调度优化问题研究[D]. 兰州：兰州交通大学，2014.

[2] 张汝成，王广生，聂玉同. 电梯系统的高精度S 型速度曲线的生成和实现[J]. 起重运输机械，2009(4):6-10.

[3] 刘筱，吴文江，郑飂默. 柔性S 型加减速控制算法研究[J]. 组合机床与自动化加工技术，2013(3):66-69.

[4] 陈建安，郭大伟，徐乃平,等. 遗传算法理论研究综述[J]. 西安电子科技大学学报，1998(6):363-367.

[5] 李晓辉，邬义杰，冷洪滨. S 曲线加减速控制新方法的研究[J]. 组合机床与自动化加工技术，2007(10):50-53.

[6] 张超勇，饶运清，李培根,等. 求解作业车间调度问题的一种改进遗传算法[J]. 计算机集成制造系统，2004(8):966-971.

[7] 罗勇，陈治亚. 基于改进遗传算法的物流配送路径优化[J]. 系统工程，2012(8):118-123.

[8] 刘巍巍，赵红，王迎春. 遗传算法在自动化仓库路径调度问题中的应用[J]. 沈阳工业大学学报，2008(6):338-341.

[9] 王厅长，邱建东，商庆健,等. 病毒协同进化遗传算法在自动化立体仓库货位优化中应用的研究[J]. 计算机科学，2014(11):35-38.

[10] 李建锋，彭舰. 云计算环境下基于改进遗传算法的任务调度算法[J]. 计算机应用，2013(11):184-187.

[11] 赵亮，宋宇博，蒋兆远. BP 神经网络在机场货运站生产调度中的应用[J]. 起重运输机械，2009(11):39-42.