战斗力形态演化的分形模型

孙巨为，王志新，王小强

（陆航研究所，北京101121）

0 引言

分形理论是专门研究分形的几何特征、数量表征及其规律和应用的科学，对于解决复杂系统问题非常有效。分维是分形理论中的最重要概念，它把分形客体的维数概念从整数扩展到了实数，实现了人类对维数概念认识的重大突破。战斗力是一个典型的复杂系统，用分形理论对其加以研究，能够在理论和实践上解决许多悬而未决的难题，如战斗中各种支离破碎的现象之间存在着某种有机的联系等。

目前，运用复杂系统理论研究战斗力已经成为军事理论研究的热点。文献［1－3］界定了战斗力、战斗能力、战斗潜力和战斗效能之间的关系，即：战斗力是战斗能力在战时表现出来的结果；战斗能力是部队遂行战斗任务的基本能力；战斗潜力是战斗能力可能表现出来的最大值；战斗效能是部队发挥战斗能力完成战斗任务的程度。文献［4－5］描述了物质化、能量化和信息化等战斗力具体形态，构建了数字化部队战争系统模型分解图，将战斗能力分解成部队与武器、电子信息、决策指挥和后勤保障等能力。文献［6－9］提出了战斗力系统演化的开放性、非平衡性、非线性等自组织特征，从内在机制上阐释了科学技术在战斗力系统向有序演化过程中起第一作用（序参量）的机理，战斗能力贡献度和依赖度与战斗体系结构演化涌现效应的联系，以及演化后各种战斗能力指标。这些观点分别从不同角度描述了战斗力形态的演化问题，尽管其中也有分形思维和思想，但都未对战斗力形态演化的分形本质加以研究。文献［10－11］等论述了城市人口和城市规模演化的分形特性，对于研究与之类似的战斗力形态演化分形模型具有重要的参考价值。

本文以分形理论为背景，将战斗力作为一个高度自治的复杂系统，论证其生成、保持、变化和衰减等分形模型，同时说明兰彻斯特方程、奥西波夫方程和战斗力指数模型的实质和来源，结合战斗实例用定量方法探讨战斗力各要素相互作用的分形机理，进而提出战斗力形态演化的分形思想。

1 战斗力相关问题描述

战斗力是战斗力系统的简称，是指武装力量遂行战斗任务的能力，由人、武器装备和人与武器装备的结合等基本要素构成［12］，具体表现为各种战斗力要素的综合，包括突击力、打击力、保障（含信息、指挥、机动、防护、后装保障）力等要素；战斗效能是战斗力量在战斗进程中发挥有效作用的程度，也是反映和评价部队战斗力的尺度与标准［12］；战斗力形态是指战斗力结构、环境及其相互关系的总体；战斗力形态演化是指战斗力的结构、状态、特性、行为和动能随着战斗进程的推移而发生的变化。

自治系统的功效是其主动通过与所在环境相互作用，实现自身目标，强调服从某些人或其它要素的控制，不能完全按照各要素自身的主观意志行事。显然，战斗力既是一种有人参与的动力系统，也是一种典型的自治系统。按照一般系统论的观点［13］，对于最简单的战斗力系统而言，战斗力要素相关作用过程可用微分方程组（1）描述，即

其中，xi（i＝1，2，…，n） 为第i个要素；fi为xi变化时所有要素x1，x2，…，xn之间的相关作用算子，与指挥、行动和协同等方式有关；xi0为第i个要素的初值（常数），可理解为经过战斗部署的战斗力要素初始值，例如，遂行突击、打击或保障等任务的战斗成员配置、状态和数量等。

该方程组既说明了各要素之间相互关联，互为因果，也说明了任何一个要素变化都以某种形式引起所有要素变化，从而导致战斗力整体向前演化。例如，保障力增强后，可使打击力也增强，而打击力增强，可更好地压制和毁伤威胁突击行动的目标，这又使突击力增强，打击力和突击力都增强后，就有利于大量歼敌，也能使保障成员和设备受到的威胁减少，进而使保障力得以保持和增强，打击力、突击力和保障力都增强后，整体战斗力必然有一个跃升。

2 战斗力生成分形模型

战斗力生成是指在战斗部署中各要素相互作用，使战斗力从无到有、从小到大的过程。战斗力生成的分形模型是用分形方法揭示战斗力结构演化性的内在机理，描述情报搜集与分析、任务要求与区分、力量编组与配置、资源筹措与配送等对战斗力生成的影响。由式（1），如果战斗力只有两个要素，则

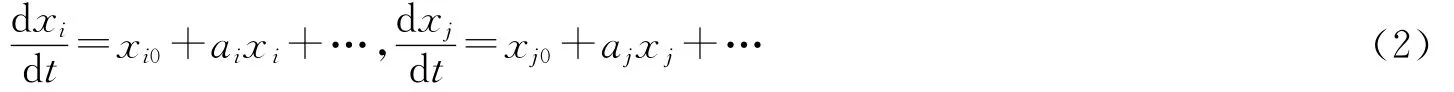
其中，xi0和xj0分别为第i个和第j个要素的初值，均可认为趋近于0，即在战斗部署前任何战斗成员和武器装备都不具备战斗力，只有战斗；ai和aj分别为第i个和第j个要素的生成系数，即战斗部署合理性系数，战斗部署越合理，该系数就越大，越容易生成战斗力，反之亦然。

显然，战斗力形态具有非线性特征，对式（2）约简，有［13］

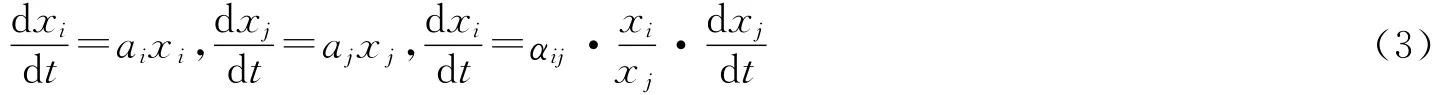
式（3）反映了两个要素之间的生成关系。当αij＞1时，第i个比第j个要素生成快；当αij＜1时，第i个比第j个要素生成慢；当αij＝1时，第i个与第j个要素同步生成。又由式（3），时刻t第i个和第j个要素的解为

将式（4）中时间项消元并化简，得第i个和第j个要素的幂指数生成模型为

式（5）是一个广义的分形模型。由于αij为第i个和第j个要素互为测度的结果，故αij具有分维性质，这里称之为“互维数”。

由式（5），得时刻t所有要素的幂指数生成模型为

式（6）是对非线性战斗力进行半线性分解的结果，简化了内部关系，保持了主要的非线性特征，近似反映了第i个要素与其它要素的生成关系。

如果战斗力包括n个要素xi（i＝1，2，…，n） ，则时刻t战斗力的一般生成模型为

其中，g为各战斗力要素的相互关系算子，该算子决定于指挥、行动和协同等方式。

对式（7）求全微分并做等价变换，得

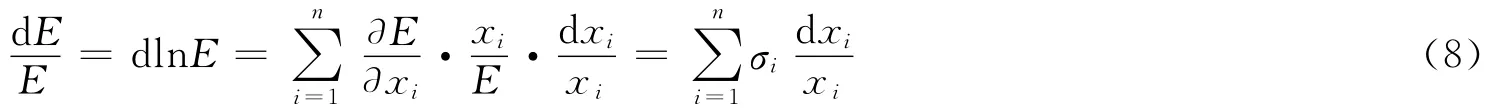
不难看出，σi＝∂E／∂xi·xi／E，为第i个要素与战斗力的关联系数，具有分维性质，分形维数为，且为常数，即认为式（8）是线性模型。对式（8）求积分得战斗力的生成模型为

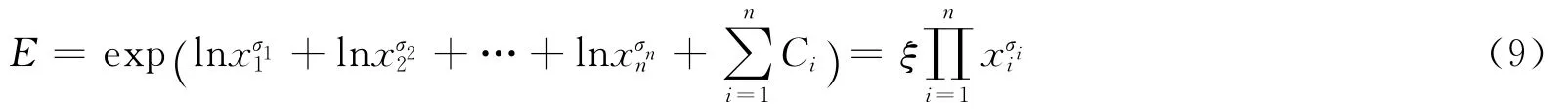
将式（5）代入到式（9）中，得战斗力的生成模型为

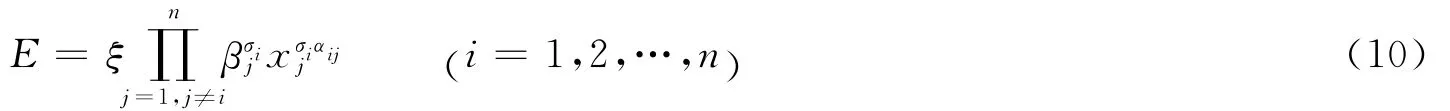
式（10）中，维数σi≠σj（i≠ j）为第i个要素发挥作用的程度，即灵敏度指数。该式说明战斗力随各要素的生成而生成，具有自仿射特征，并可化为任意多个xi的σi次幂的乘积形式。

3 战斗力保持分形模型

战斗力保持是指在战斗实施中各要素逐步适应战场情况，使战斗力保持最大状态的过程。其分形模型是用分形方法揭示战斗力结构稳定性的内在机理，描述当前态势与任务、力量配比与分配、战法选择与运用、时空协调与协同等对战斗力保持的影响。由式（7）和式（9），在时刻t，有

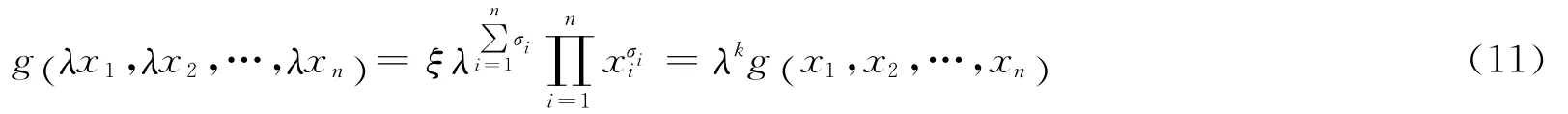
式（11）说明战斗力是一个k次齐次函数，即：如果所有要素都变化λ倍，则战斗力同方向变化λk倍。特别是，当k＝1时，该战斗力是线性齐次函数。例如，如果x1，x2，…，xn全部同时增加为λx1，λx2，…，λxn，则战斗力E将增加为λkE，即：当λ＞1时，E递增；当λ＝1时，E不变；当λ＜1时，E递减。然而，如果要素数量n＞2且k为实数域的任意数值，则战斗力与各要素之间不满足线性关系。为此，用欧拉齐次函数定理确定式（11）中在λ＝1时的表达式，即

由式（12），当k＝1时，战斗力最大值为

由式（9），如果各要素总量为X，则当k≠1且存在条件函数时，战斗力最大值为

式（14）的拉格朗日函数为

其中，γ为拉格朗日参数。

由式（14）和式（15），用拉格朗日乘数法可求取战斗力极值。存在极值条件的联立方程组［14］为

求解联立方程组得战斗力有最大值的条件和解析解为

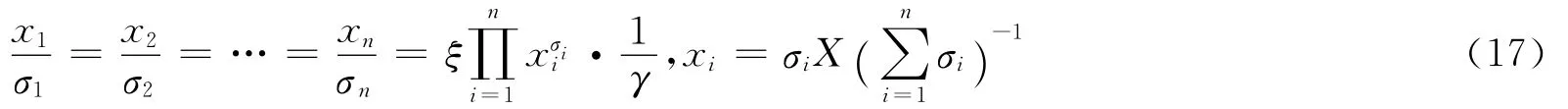
4 战斗力变化分形模型

战斗力变化是指在战斗相持中因某个要素不能发挥作用，使战斗力突然增大或减小的过程。其分形模型是用分形方法揭示战斗力结构适应性的内在机理，描述敌我博弈与对抗、策略改变与调整、战机创造与把握、环境利用与规避等对战斗力变化的影响。这种现象是系统分形特性退化，有两种模式，即：

第一，在时刻t某个要素变化与该要素大小无关，只取决于战斗力的各种限制条件。

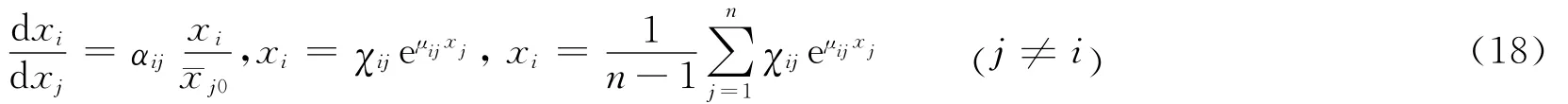
以第1个要素受到限制为例说明战斗力变化现象。将式（18）代入式（9）得战斗力的变化模型为

比较式（10）和式（19），可判别该模式下战斗力变化方向，即

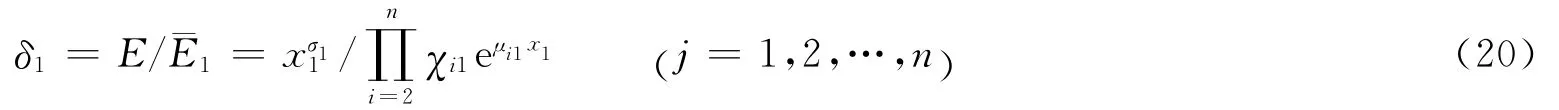
式（20）显然有“指数函数的增大‘速度’比幂函数快得多”［14］，即战斗相持到一定程度后，式（20）中任何一项δ1＜1。这说明指数函数模式的战斗力大于幂函数模式，即由E向上变化为，原因是式（18）中，虽然第j个要素受到限制，但仍可使第i个要素以指数函数增大，使式（19）的战斗力最终向增大方向变化。如，当兵力突击受挫时，可通过增强火力打击或综合保障等提高整体战斗力。

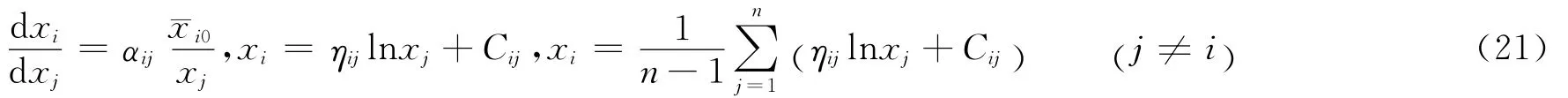
以第1个要素受到限制为例说明战斗力变化现象。将式（21）代入式（9）得战斗力变化模型为

比较式（22）和式（10），可判别该模式下战斗力变化方向，即

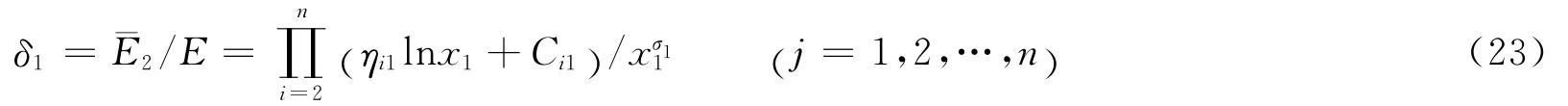
式（23）显然有“幂函数的增大‘速度’比对数函数快得多”［14］，即战斗相持到一定程度后，式（23）中任何一项δ1＜1。这说明对数函数模式的战斗力小于幂函数模式，即由E向下变化为，原因是式（21）中，虽然第i个要素受到限制，但第j个要素使其以对数函数减小，使式（19）的战斗力最终向减小方向变化。如，当兵力突击受挫时，未能有效组织与之协同的火力打击或综合保障等行动，兵力突击效果将会进一步下降，导致整体战斗力下降。

第二，时刻t两个要素变化与这两个要素的大小无关，只取决于战斗力的各种限制条件。

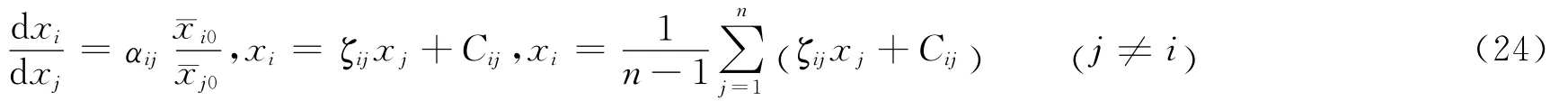
其中，ζij＝αiji0／j0，为常数；Cij为积分常数。

以所有要素受到限制为例说明战斗力变化现象。将式（24）代入（9）得战斗力变化模型为

比较式（25）和式（10），可判别该模式下战斗力的变化方向，即

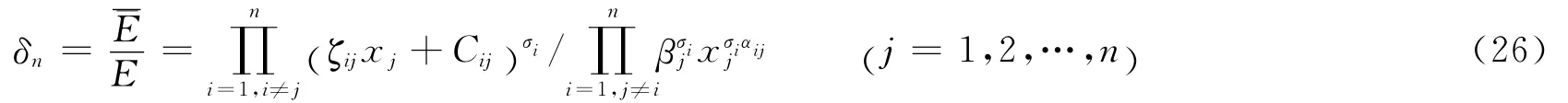
显然，δn的增减方向可由必达法则判定，其值与ζij，Cij，σi，βj和αij等有关。

5 战斗力衰减分形模型

战斗力衰减是指在战斗决胜中因某些条件不再具备，使战斗力不断消耗直至殆尽的过程。其分形模型是用分形方法揭示战斗力结构脆弱性的内在机理，描述战斗成员伤亡、武器弹药消耗、指挥控制失效、战场环境不利、战斗精神崩溃等复杂因素对战斗力衰减的影响。如果在时刻t第j个要素为（大于0的常数），第i个要素为（大于0的常数），并将之作为初值，则式（1）可表述为

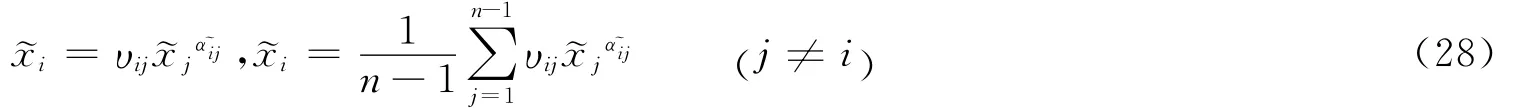
由式（9），得战斗力衰减模型为

6 战斗力分形模型特例

长期以来，许多学者对战斗力形态演化问题进行过研究，并给出了各种比较实用的演化模型［15－16］。从结构特点上看，这些模型都是战斗力形态演化分形模型的一种特例或派生形式。主要有：

2）奥西波夫战斗方程。由式（29），当i＝1，σ1＝1.5，其他参数含义和取值不变时，有，该结果与奥西波夫方程中A，B方战斗效能等价，即“A方损失＝K·（B方实力）p”和“B方损失＝K·（A方实力）p”。其中，K为比例系数；p为凭经验确定的指数。

上述特例说明，战斗力形态演化分形模型不只是一种抽象的理论模型，还是一种能够指导战斗实践的可派生模型，根据战斗需要和相关数据，可以派生出不同结构和精度的模型。

7 战斗力分形模型应用

分析式（9）、（14）、（22）、（25）和（29）不难发现，各战斗阶段战斗力形态具有很强的“伸缩性”，当只考虑某要素与整体的关系时，其余要素信息均“压缩”在了系数或参数当中。

7.1 战斗力测度关系模型

为了将上述战斗力模型解析为具体的测度关系模型，并利用其中的自仿射性质，变量选择应遵循可观测、能甄别、有代表性的原则。为此，可将战斗效能（用敌方伤亡战斗成员数表征）作为战斗力的输出变量，将战斗实力（包括突击实力、打击实力和保障实力，用我方相应的战斗成员数表征）作为战斗力的输入变量，由此可建立如下战斗力各要素实力和战斗效能之间的数理关系。

突击实力与打击实力、打击实力与保障实力、保障实力与突击实力之间异速生长关系为

其中，xt，xd和xz分别为突击实力、打击实力和保障实力，战斗实力X0＝xt＋xd＋xz。

基于战斗实力、突击实力、打击实力和保障实力等单项的战斗效能弹性模型为

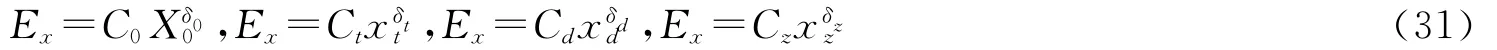
基于突击实力、打击实力和保障实力等综合的战斗效能弹性模型为

其中，adt，azd，atz，bdt，bzd，btz，C0，Ct，Cd，Cz，δ0，δt，δd，δz，η，ht，hd，hz均为参数，不难得到，hd＝δd／3，hz＝δz／3。

假定相应于xt，xd，xz和Ex的广义维数分别为Dxt，Dxd，Dxz和DEx，由几何测度关系知

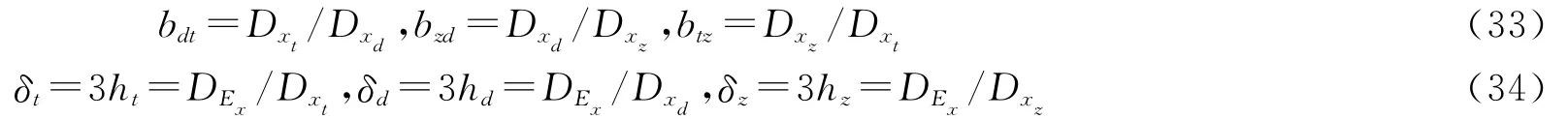
由式（33）和（34）可得

因此，只要bdt，bzd和btz不是整数或整数之比，δt，δd，δz，ht，hd和hz就具有分维性质。

7.2 战斗力测度关系实例

现以我军历史上某次陆军战役中陆军第×师进攻战斗为例，说明战斗力各要素的测度关系。该师战斗目的是歼灭当前守敌一个团大部，为友邻实施战役纵深战斗创造条件。该师已完成战斗部署，于19××年×月×日拂晓用火力准备的方式触发战斗，包括火力准备、前沿突击、抗反冲击、分割围歼、纵深战斗、追击残敌、清剿战场等阶段。根据战斗日志，该师战斗共进行8昼夜，每个战斗日敌我战斗实力变化如表1所示（注：表中假设情况供辅助分析）。

将表1中点列数据 （X0（t），Ex（t） ） 、（xt（t），Ex（t） ） 、（xd（t），Ex（t） ） 和 （xz（t），Ex（t） ） 分别标绘于对数坐标图中，其分布呈对数线性分布趋势，如图1～图4所示。将表1中点列数据 （X′0（t），Ex（t） ） 绘于对数坐标图中，其分布呈对数线性分布趋势相对较差，如图5所示。

可根据式（30）和（31）的双对数形式和表1数据，利用最小二乘法计算有关参数。这样，基于战斗力、突击力、打击力和保障力等单项的战斗效能动力相似模型为

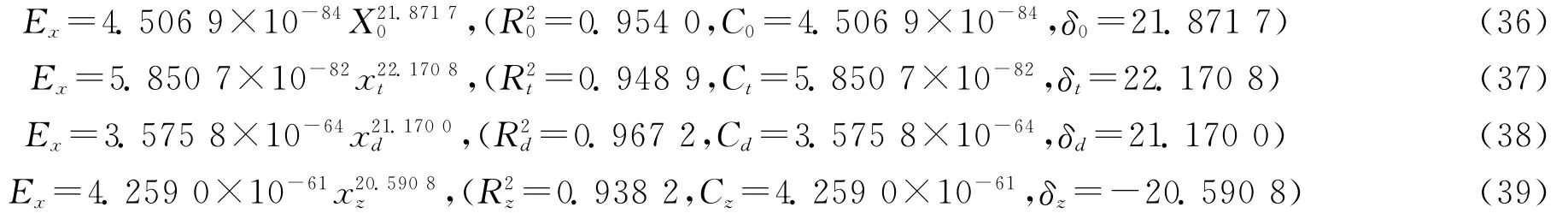
突击力与打击力、打击力与保障力、保障力与突击力的异速生长关系分别为

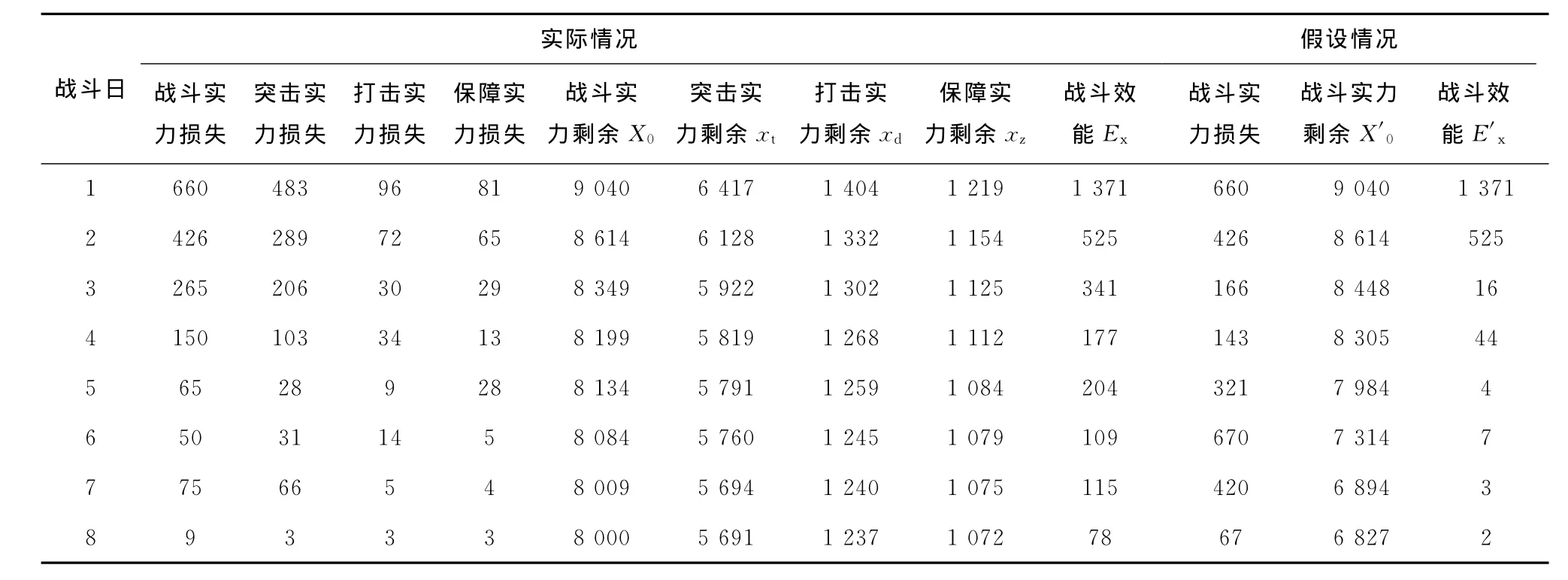
表1 陆军第×师进攻战斗各战斗日敌我双方战斗力相关数据统计Tab.1 The related date statistics of a attack battle of the army′s division

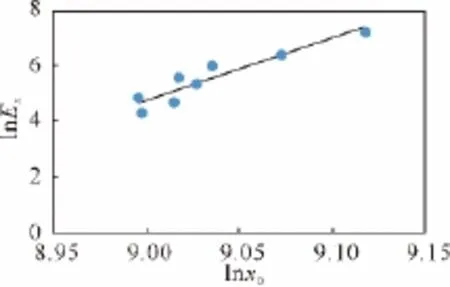
图1 战斗实力与战斗效能对数关系（实际情况）Fig.1 Logarithmic relationship between combat power combat effectiveness（Actual situation）

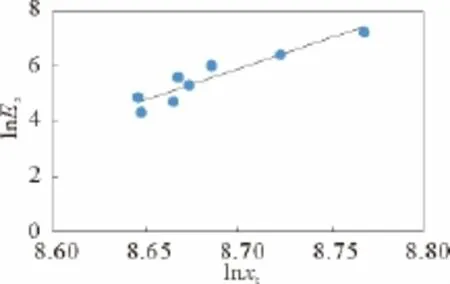
图2 突击实力与战斗效能对数关系（实际情况）Fig.2 Logarithmic relationship between assault power and combat effectivenss（Actual situation）

图3 打击实力与战斗效能对数关系（实际情况）Fig.3 Logarithmic relationship between force power and combat effectiveness（Actual situation）

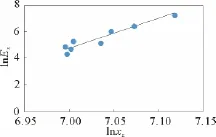
图4 保障实力与战斗效能对数关系（实际情况）Fig.4 Logarithmic relationship between support power and combat effectiveness（Actual situation）

图5 战斗实力与战斗效能对数关系（假设情况）Fig.5 Logarithmic relationship between combat power and combat effectiveness（Hypothetical situation）

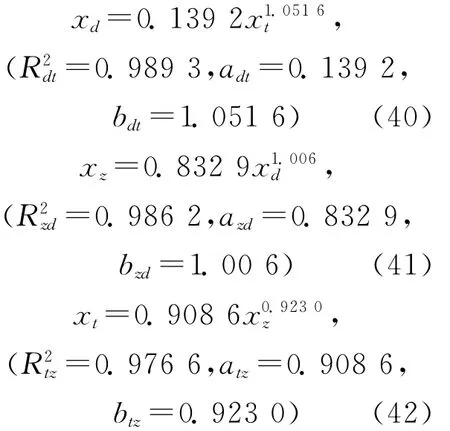
由式（32）可计算得η＝4.466 5×10－69，ht＝7.390 2，hd＝7.056 7，hz＝6.863 6。这样，基于突击力、打击力和保障力等综合的战斗效能弹性模型为

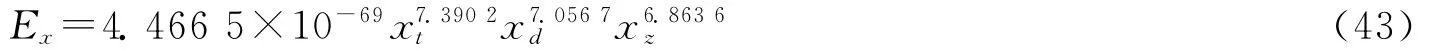
由表1实际情况数据和理论模型知：bdt＝1.051 6，δt＝22.170 8，δd＝21.170 0，δt／δd＝1.047 3，ht／hd＝7.390 2／7.056 7＝1.047 3，满足式（35）。将表1中xt、xd和xz数据代入式（37）、（38）和（39）中，计算结果与表1中相应的Ex值基本一致，联系到双对数坐标图的点列分布状态（图1～4），可认为该师战斗力形态演化具有自仿射的分形结构。而且，ht，hd和hz具体数值均为非整数或整数之比，系统是分数维的。

根据表1假设情况数据和最小二乘法，可计算得战斗实力与战斗效能的动力相似模型为

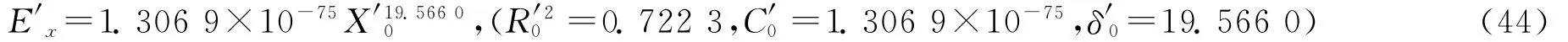
显然，由式（36）～式（44）可知，相关指数R′20≪R20，说明战斗力分形特性出现了退化，表现为第3～第8个战斗日伤亡较大，其原因一般是情报不准、决策失误、执行不力、敌人善战等，其本质是战斗力各要素大小及其关系发生了变化，使预期战斗力分形结构遭到破坏。又可知，变量指数或维数δ′0≪δ0，说明两种情况的战斗力系统结构不一样。根据分形理论，维数越大，系统结构就越复杂，系统运行效率也越大，但对系统结构可靠性提出了较高要求，因为系统结构一旦破坏就很难恢复。因此，制定战斗方案时应考虑多种情况协同，强化战斗预备队和临机决策的作用等。

8 结语

战斗力形态演化的分形特性是大自然分形特性的具体表现，是战斗力固有的基本性质。对于预期的战斗力，战斗力形态演化的分形模型可表述成战斗力各要素相关的幂指数函数形式，具有自仿射特征。只有保持生成系数比与相应战斗力构成要素的比值恒定，才能使战斗力最大。如果外部和内部条件不能满足有关要求，则战斗力形态演化将会发生重大变化，即战斗力突然增大或减小，这往往意味着战机将要出现。因此，运用分形理论研究战斗力，不仅有助于揭示战斗力的本质和规律，阐释克敌制胜的机理和方法，而且还可使战斗方案和战斗组织更加合理，针对破坏战斗力分形结构的因素进行分析，从而创造和把握战机，为化解战场危机、探索制胜机理提供依据。

［1］ 胡晓峰，杨镜宇，司光亚，等.战争复杂系统仿真分析与实验［M］.北京：国防大学大学出版社，2008：279－384.

［2］ 胡晓峰，司光亚，吴琳，等.战争模拟引论（上）［M］.北京：国防大学大学出版社，2004：191－199.

［3］ 胡晓峰，罗批，司光亚，等.战争复杂系统建模与仿真［M］.北京：国防大学大学出版社，2005：385－391.

［4］ 刘西山.战斗力本质论［D］.江苏：南京陆军指挥学院，2008.Liu Xishan.The essence of fighting capacity［D］.Jiangsu：Nan Jing Army Command College，2008.

［5］ 胡军，李涛，李亮，等.数字化部队作战能力评估指标体系［J］.火力与指挥控制，2009，34（9）：76－83.Hu Jun，Li Tao，Li Liang，et al.Research on combat capability evaluation guideline system of digitization troop［J］.Fire Control and Command Control，2009，34（9）：76－83.

［6］ 宋黎.战斗力系统自组织演化分析［J］.南京政治学院学报，2005（6）：45－50.Song Li.Analysis on the self－organized evolution of combat capability systems［J］.Journal of PLA Nanjing Institute of Politics，2005（6）：45－50.

［7］ 宋黎.科学技术第一战斗力的系统分析及实现途径［D］.辽宁：大连理工大学，2007.Song Li.Analysis and approach of system of science and technology of the first combat［D］.Liaoning：Dalian University of Technology，2007.

［8］ 夏璐，邢清华，范海雄，等.基于能力关系的作战体系结构演化涌现效应［J］.火力与指挥控制，2013，38（7）：42－45，49.Xia Lu，Xing Qinghua，Fan Haixiong，et al.Research on emergence effect in evolution of operational system－of－systems architecture based on capability relationship［J］.Fire Control ＆Command Control，2013，38（7）：42－45，49.

［9］ 温睿，马亚萍，王峥，等.一种作战体系动态演化模型［J］.系统仿真学报，2011（7）：85－92.Wen Rui，Ma Yaping，Wang Zheng，et al.Dynamic evolution model of a combat system［J］.Journal of System Simulation，2011（7）：85－92.

［10］De Kcersmaecker M－L，Frankhauser P，Thomas I.Using fractal dimensions for characterizing intra－urban diversity：the example of Brussels［J］.Geographical Analysis，2003，35（4）：310－328.

［11］Benguigui L，Czamanski D，Marinov M，et al.When and where is a city fractal？［J］.Environment and Planning：Planning and Design，2000，27（4）：507－519.

［12］全军军事术语委员会，军事科学院.中国人民解放军军语［Z］.北京：军事科学出版社，2011：10.

［13］冯·贝塔朗菲著.一般系统论的基础、发展和应用［M］.林康义，魏宏森，译.北京：清华大学出版社，1987：52－55.

［14］同济大学数学系.高等数学（第六版上册）［M］.北京：高等教育出版社，2007：137.

［15］王辉青.中国军事百科全书（第二册）军事运筹（学科分册）［M］.北京：中国大百科全书出版社，2007：45－99.

［16］凌云翔，马满好，袁卫卫，等.作战模型与模拟［M］.湖南：国防科技大学出版社，2006：126－185.

［17］张效成，张阳，徐锬.经济类数学分析（下册）［M］.天津：天津大学出版社，2005：68－156.

［18］孙巨为.作战力量体系优化问题研究［D］.河北：石家庄陆军指挥学院，2011.Sun Juwei.Research on the optimization problem of combat power system［D］.Hebei：Shijiazhuang Army Command College，2011.

［19］金伟新，肖田元.作战体系复杂网络研究［J］.复杂系统与复杂性科学，2009，6（4）：12－25.Jin Weixin，Xiao Tianyuan.Research on the combat SoS complex network［J］.Complex Systems and Complexity Science，2009，6（4）：12－25.

［20］БусленкоН П.Моделированиесложныхсистем［M］.Москва：Издатериство《Наука》，1978：24－121.

［21］Dean J R.Warfare analysis laboratory 2000［J］.Johns Horkings Apl Technical Digest，2000，21（2）：231－237.

［22］Moffat J.Complexity Theory and Network Centric Warfare［M］.Washington：CCRP Press，2000：65－89.

［23］James M T.On integration and adaptation in complex service systems［J］.Journal of Systems Science and Systems Engineering，2008，17（4）：48－54.