正八边形多胞薄壁管吸能特性仿真和优化＊

白中浩，王飞虎，郭厚锐

（湖南大学 汽车车身先进设计制造国家重点实验室，湖南 长沙 410082）

金属薄壁结构以其成本低、吸能效率高等特点，在航空和汽车工业上的应用越来越广泛．在过去数十年中，国内外针对金属薄壁结构进行了大量的研究，从试验、理论和数值分析方面探究了不同加载条件下的金属薄壁结构的吸能特性．然而，过去大部分研究工作都集中在圆形、方形或矩形截面金属薄壁结构上［1－4］．

近年来，具有多个胞元的新型薄壁结构受到关注［5－10］．Chen等人［5］于2001年率先在理论和数值分析方面研究了轴向加载下双胞和三胞铝制品结构的冲击优势．Zhang等人［6］比较研究了多胞结构和泡沫填充结构的吸能效率．Najafi等人［7］对不同截面方形多胞结构的吸能特性进行了研究．亓昌等人［8］研究了锥形多胞薄壁管斜向冲击下的吸能特性．上述研究都表明：多胞薄壁结构与单胞或填充材料结构相比，具有更高的吸能效率．然而，到目前为止，关于非直角与板组成的多胞结构的研究较少．

Rossi等人［11］研究发现，在截面面积和厚度相同的情况下，八边形薄壁结构比四边形薄壁结构的平均碰撞力增加了25%，吸能变形量降低了20%．Fan等人［12］研究表明，八边形薄壁管变形均匀，吸能特性较好．张宗华等人［13］研究了等周长的不同截面形状多边形薄壁结构的轴向冲击性能，发现多边形薄壁管的平均冲击力和吸能特性随着多边形顶点的增加而提高，但八边形以后基本趋于稳定．作者之前设计了一种八边形逐级吸能结构，有效地改进了某越野车前纵梁的碰撞性能［14－15］，现针对八边形薄壁结构以及多胞结构具有结构紧凑和高效吸能的特点，研究了一种边对边（two side to side，S2S）布置的正八边形多胞管S2S结构，该结构同时结合了八边形管的结构紧凑和多胞管的高比吸能特性．通过一系列仿真探讨了不同截面形状和结构参数对吸能特性的影响，并根据吸能特性指标对正八边形多胞管S2S结构进行了优化，优化后其吸能特性明显提高，为此类结构的优化设计和工程应用提供参考．

1 问题描述

1．1 物理模型

本文研究的对象为正八边形多胞管S2S结构，如图1所示．长度L为210mm，正八边形截面边长d为40mm，壁厚t都为1mm．底端采用固定支承，上端承受刚性墙以恒定速度轴向压缩，速度大小为V．

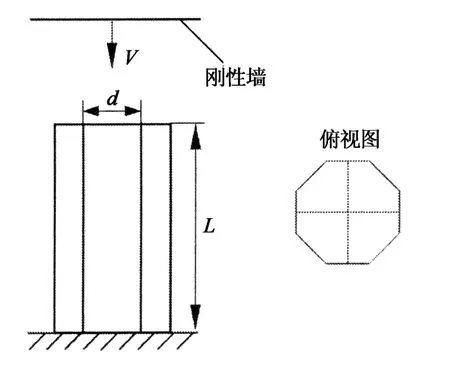
图1 正八边形多胞管轴向压缩示意图Fig．1 Schematic diagram of octagon multi－celltubes under axial compression

1．2 结构吸能特性指标

一般来说，分析结构吸能特性的关键参数主要有：总吸能量（E）、比吸能（SEA）、平均压溃力（Fav）、最大压溃力（Fpeak）等．比吸能SEA是评价一个结构的能量吸收效率的指标，用来描述结构单位质量吸收的冲击能量，可表示为：

式中：M为结构的质量；E为结构吸收的总能量，其值可以通过对力－位移曲线积分得到．

式中：d为结构的有效变形量．

平均压溃力为Fav，其表达式如式（3）所示．由此式可以计算出平均压溃力随时间的变化趋势．

最大压溃力是指薄壁结构在压溃过程中的初始压溃载荷峰值，即薄壁结构与刚性墙初始接触时峰值载荷Fpeak．

2 仿真模型

2．1 有限元建模

采用有限元软件Abaqus／Explicit，建立了正八边形多胞薄壁管模型．如图2所示，顶部刚性平面以恒定的速度5mm／min轴向压缩多胞管，多胞管底部与另一刚性平面焊接连接，底部刚性平面固定．多胞管采用四节点壳单元S4R模拟，综合考虑精度和求解效率，壳单元沿厚度方向取5个积分点，单元特征长度取2．5 mm．多胞结构的材料为H300Lad钢，密度ρ＝7 850 kg／m3，弹性模量E＝210GPa，泊松比ν＝0．3．H300Lad钢材的真实应力－应变曲线如图3所示．

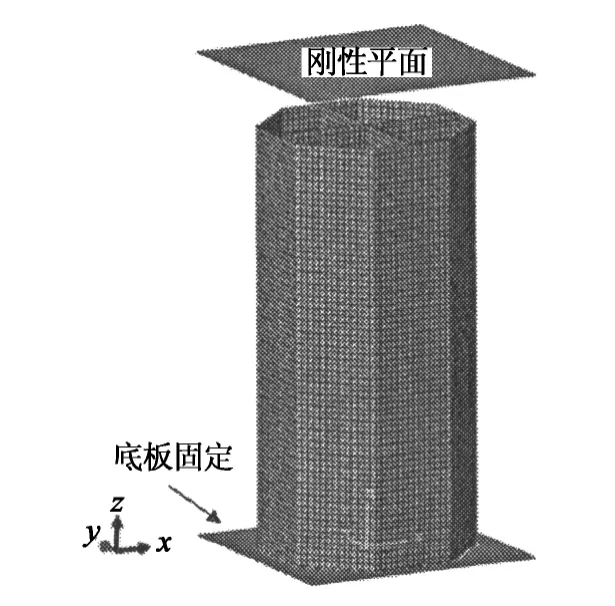
图2 正八边形多胞管有限元模型Fig．2 Finite element model of octagon multi－cell tube

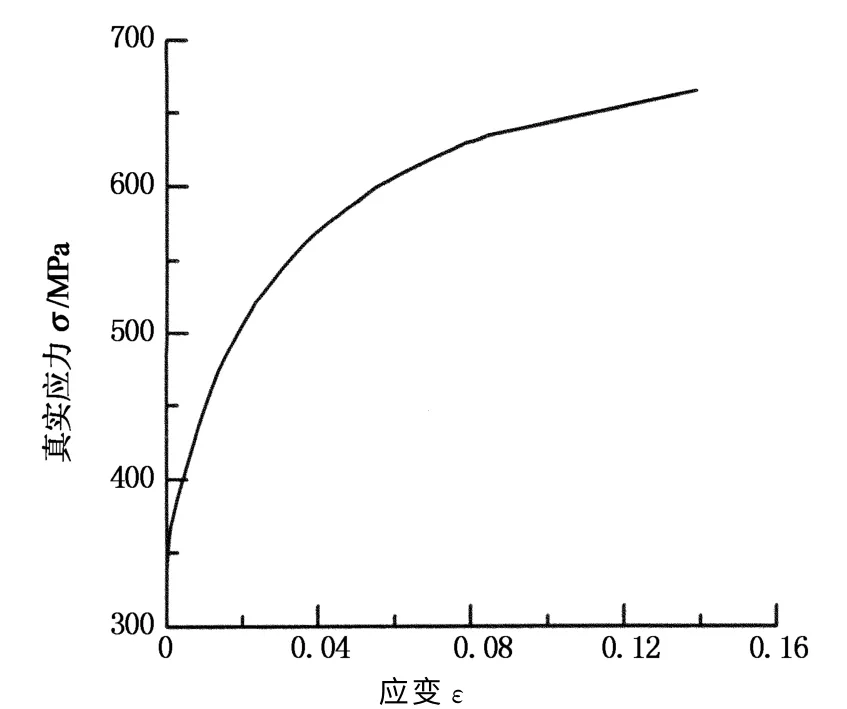
图3 真实应力－应变曲线Fig．3 Ture strss－strain of specimens

2．2 有限元模型验证

为了验证有限元模型，根据文献［12］的实验模型参数，对正八边形单胞管进行准静态轴向压溃仿真．图4为本文有限元仿真结果与文献［12］中的实验结果对比，从图中可以看出，力响应曲线的峰值、峰值出现时刻以及波动趋势基本一致，变形模式方面存在一定的误差，但误差在可接受范围内．因此，本文所建模型有效，可用于后续的研究．

图4 正八边形单胞管仿真与试验结果对比Fig．4 Simulation and experimental results comparison of octagon single－cell tubes

3 仿真结果与分析

3．1 截面形状对吸能特性的影响分析

图5为几种几何参数相同而截面形状不同的正八边形薄壁管示意图，单胞管命名为SO（single－cell octagon）；2种不同截面形状的四胞管分别命名为S2S（two side to side）和C2C（two corner to corner）；2种不同截面形状的八胞管分别命名为S4S（four side to side）和C4C（four corner to corner）．通过对不同截面形状的多胞管进行仿真分析，仿真结果如表1所示．

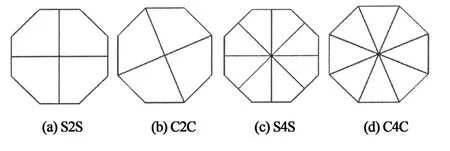
图5 正八边形薄壁管不同截面形状示意图Fig．5 Different cross sections shape of octagon thin－walled tubes

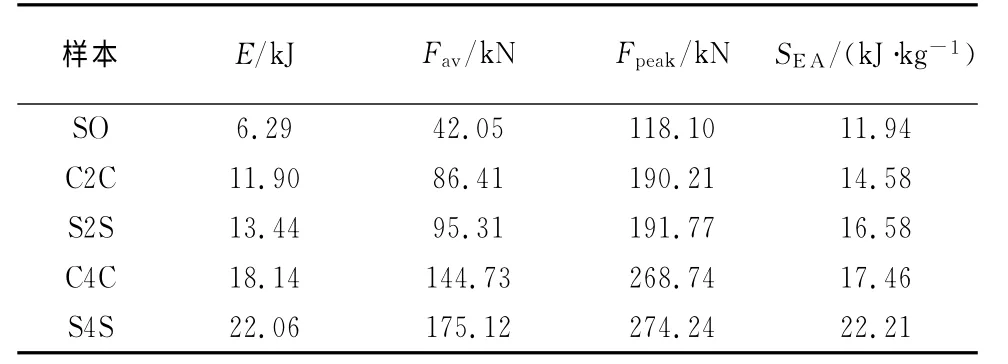
表1 多胞管数值分析结果Tab．1 Results of simulation for multi－cell tubes

从表1可以看出，平均压溃力Fav随着胞管数增加而增大．S4S 结构的平均压溃力是SO 结构的4倍多．不同截面形状的同胞数结构的平均压溃力也不同，如同胞数的S2S结构与C2C 结构相比，平均压溃力增加了10．3%．这是由于不同截面形状导致出现不同的变形模式，当结构中连通边为3的角单元在夹角小于120°时，随着夹角的增大，平均压溃力明显增加［16］．

最大压溃力Fpeak随着薄壁管胞数的增加而明显增大，S4S 结构的最大压溃力Fpeak最大，达到了274．24kN，是SO 结构的2倍多，比S2S结构增加了43%．同时，S2S与C2C结构以及S4S与C4C 结构相比，最大压溃力都略大些．其中，C4C 结构的最大压溃力比S2S结构增加了40．14%．

多胞管的比吸能明显高于单胞管，这是由于薄壁管胞数增加后，管内部增加了交叉板，这需要更多的能量来使之变形．此外，S2S与C2C结构以及S4S与C4C 结构相比，比吸能分别增加了13．7%和27．2%，这与结构的截面布置形式有关，同胞数管边对边的布置形式（side to side，见图5（a）和图5（c））相比角对角布置形式（corner to corner，见图5（b）和图5（d）），增加了拐角的数目，随着拐角数目的增大，产生塑性变形需要耗散的总能量就越多．然而，C4C结构的比吸能比S2S结构只增加了5．3%，说明截面形式不同对多胞结构比吸能影响较大，边对边的布置形式比角对角布置形式的吸能效果更好．

3．2 结构参数对吸能特性的影响分析

在正八边形多胞管S2S 结构基准模型的基础上，研究结构几何参数对多胞管吸能特性的影响．依据汽车车身结构中典型薄壁管件尺寸，各参数取值如表2所示．

表2 正八边形多胞管几何参数取值Tab．2 Geometry parameters of octagon multi－cell tubes

3．2．1 壁厚对S2S结构的影响

保持截面尺寸不变，首先分析壁厚对S2S结构的影响．图6为准静态压缩下壁厚t对多胞管S2S结构比吸能的影响．可以看出，随着壁厚的增加，比吸能逐渐增大，增大幅度逐渐减小．如壁厚t从1．2 mm 增加到1．8 mm，比吸能增加了39．65%；t从1．8mm增大到2．4mm，比吸能只增加了13．77%．

壁厚对最大压溃力的影响如图7所示，最大压溃力随着壁厚的增加而单调上升，近似呈线性正相关．

图6 壁厚对比吸能的影响Fig．6 Effect of wall thickness on SEA

图7 壁厚对最大压溃力的影响Fig．7 Effect of wall thickness on peak force

3．2．2 截面尺寸对S2S结构的影响

图8为截面边长对S2S结构比吸能的影响．从图中可知，随着截面边长的增大，比吸能单调减小，近似呈线性负相关．

截面尺寸对最大压溃力的影响如图9所示，随着截面尺寸的增大，最大压溃力略微增加．如边长d从35 mm增大到45mm，最大压溃力只增长了6．87%．

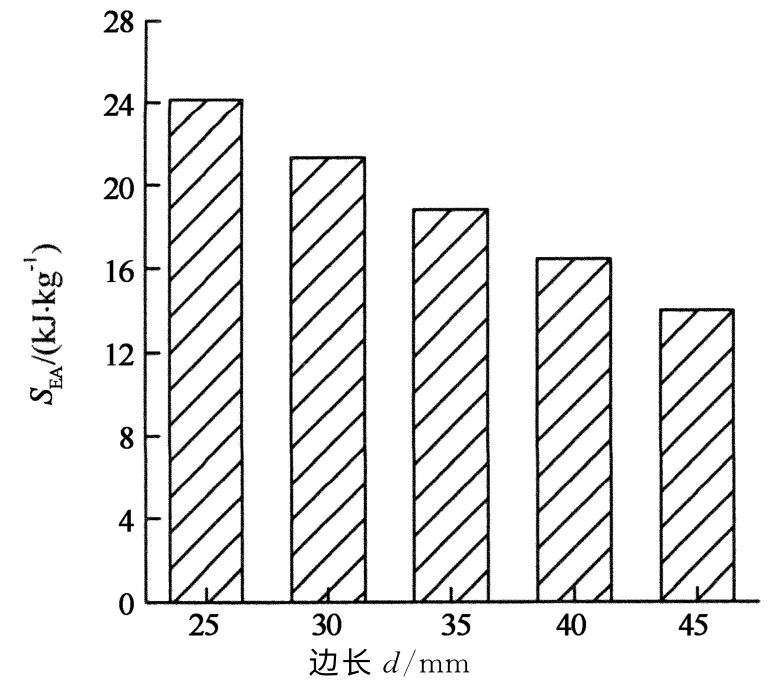
图8 截面尺寸对比吸能的影响Fig．8 Effect of section size on SEA

图9 截面尺寸对最大压溃力的影响Fig．9 Effect of section size on peak force

总的来说，各结构参数对正八边形多胞管S2S结构的吸能特性影响相互关联，彼此制约，针对具体问题，有必要对S2S结构进行优化设计得到满足需求的最优结构．

4 结构优化设计

4．1 优化问题定义

目前，提高薄壁结构吸能特性普遍采用2种方法：1）采用先进的高强度特性的材料；2）对壁厚、截面尺寸等参数进行优化．在碰撞过程中，常以最大吸能量为设计准则，但是，随着不可再生能源的日益枯竭，轻量化设计已成为当前汽车安全性设计主要考虑的因素之一，因此比吸能更加全面地表征了结构的吸能性．此外，碰撞过程中薄壁结构的最大碰撞力也直接影响到车内乘员的安全性．

上述仿真结果表明，壁厚t和截面尺寸d对多胞管S2S结果的吸能特性影响明显．为了进一步提高多胞管S2S结构的吸能特性，以多胞管S2S结构的壁厚t和截面尺寸d为优化参数；以比吸能SEA，平均压溃力Fav以及最大压溃力Fpeak为优化目标，定义多胞管S2S结构的多目标优化问题为：

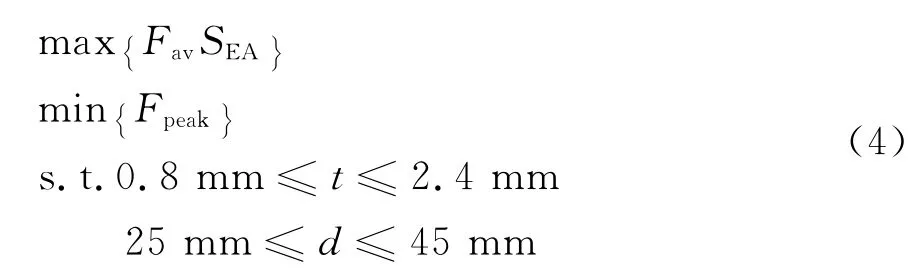
为了提高求解效率，优化过程采用二次多项式响应面模型代替有限元仿真分析，并通过优拉丁超立方试验设计（DOE）方法设计9组仿真试验，建立响应面模型．利用非支配遗传算法（NSGA－Ⅱ）［17］寻求多目标优化问题（式（4））的帕雷托最优解，优化流程如图10所示．

4．2 构建近似模型

近似模型的方法已经被证明是一种特别有效的方法，被广泛应用于薄壁管的优化设计中，如响应面模型（RSM）［18］．本文基于优拉丁超立方试验设计的试验结果，利用逐步回归方法得到优化目标关于两个设计变量的二阶多项式响应面模型的多元回归方程为：

式中：Fav，SEA和Fpeak分别为正八边形多胞管S2S结构的平均压溃力、比吸能和最大压溃力；t和d分别为多胞管的壁厚和截面边长．

图10 优化流程图Fig．10 Optimization process sketch map

平均压溃力Fav的回归方程的决定系数R2为99．97%，比吸能SEA的回归方程的决定系数R2为99．93%，最大压溃力Fpeak的回归方程决定系数R2为99．99%．由R2值可以看出，这3个二阶多项式响应面模型的拟合精度较好，能够较好地满足预测精度的要求．

表3给出了5个随机样本点的设计目标响应面模型计算值和有限元分析值．从表中可以看出，响应面模型的计算值与有限元的分析值都相当接近，相对误差不超过5%，因此，设计目标的响应面模型精度都很高，可以替代有限元模型用于后续的多目标优化设计过程．

4．3 优化结果分析

多目标优化问题最明显的特征就是不存在唯一的全局最优解，而是存在一个最优解集，称为Pareto解集或Pareto前沿．基于此解集，设计者可以根据具体问题确定最终优化方案．本文基于响应面模型，采用非支配遗传算法对回归方程进行多目标优化求解得到的Pareto前沿如图11所示．图中三角形点、圆形点和五角星点所示分别为最大压溃力、比吸能和平均压溃力的最优解．由于3个目标之间存在相互制约的矛盾，在此以比吸能为主要目标，兼顾最大压溃力和平均压溃力，选取权重分别为0．5，0．3，0．2．本多目标优化问题的最优解如图11中五边形点所示，此时设计点取整后d＝30mm，t＝1．0mm．

表3 5个样本点的近似值和有限元分析值Tab．3 The results of RSM and simulation for five sample points

图11 多目标优化问题的Pareto解集Fig．11 Pareto solution set of multi－objective optimization problem

根据优化结果，考虑到结构的吸能特性以及现有的材料和加工工艺，设计了一种正八边形多胞管S2S结构，其长度为210mm，截面边长为30mm，截面形状如图5（a）所示，壁厚为1．0mm，并对其进行了有限元仿真，仿真值与优化值的最大相对误差不超过4%，说明了设计方法具有足够高的精度．优化设计结果如表4所示，结果表明，多胞管S2S结构的比吸能比优化前提高了33．11%，平均压溃力提高了6%，最大压溃力降低了3．78%，优化效果明显．

表4 优化设计结果对比Tab．4 Comparison between optimization results

5 结 论

研究了一种用于碰撞吸能的正八边形多胞薄壁管S2S 结构，采用有限元仿真分析了截面形状（C2C，S2S，C4C 和S4S）和结构参数对吸能特性的影响，并对多胞管S2S 结构的结构参数进行了优化．研究结果表明：

1）与单胞管、多胞管C2C，C4C 和S4S 结构相比，多胞管S2S结构的吸能特性更好；边对边布置形式的吸能效果优于角对角布置形式．

2）减小截面尺寸、增加壁厚可以提高多胞管的比吸能，但壁厚的增加使得最大压溃力也随之增大；最大压溃力与壁厚呈近似线性正相关，可以通过减小壁厚和增大截面尺寸降低最大压溃力．

3）结合优拉丁超立方试验设计方法和非支配遗传算法，对多胞管S2S结构的吸能特性进行了优化设计，优化结果比初始设计的吸能特性有了较大提高，比吸能比优化前提高了33．11%，最大压溃力降低了3．78%，吸能效果更好．

［1］ABRAMOWICZ W，JONES N．Dynamic progressive buckling of circular and square tubes［J］．International Journal of Impact Engineering，1986，4（4）：243－270．

［2］HUANG X，LU G，YU T，etal．On the axial splitting and curling of circular metal tubes［J］．International Journal of Mechanical Sciences，2002，44（11）：2369－2391．

［3］TARIGOPULA V，LANGSETH M，HOPPERSTAD O S，et al．Axial crushing of thin－walled high－strength steel sections［J］．International Journal of Impact Engineering，2006，32（5）：847－882．

［4］顾红军，赵国志，陆廷金，等．轴向冲击下薄壁圆柱壳的屈曲行为的实验研究［J］．振动与冲击，2004，23（4）：58－59．

GU Hong－jun，ZHAO Guo－zhi，LU Ting－jin，etal．Buckling of thin－wall cylindrical shell under axial impact［J］．Journal of Vibration and Shock，2004，23（4）：58－59．（In Chinese）

［5］CHEN W，WIERZBICKI T．Relative merits of single－cell，multi－cell and foam－filled thin－walled structures in energy absorption［J］．Thin－Walled Structures，2001，39（4）：287－306．

［6］ZHANG X，CHENG G．A comparative study of energy absorption characteristics of foam－filled and multi－cell square columns［J］．International Journal of Impact Engineering，2007，34（11）：1739－1752．

［7］NAJAFI A，RAIS－ROHANI M．Mechanics of axial plastic collapse in multi－cell，multi－corner crush tubes［J］．Thin－Walled Structures，2011，49（1）：1－12．

［8］亓昌，董方亮，杨姝，等．锥形多胞薄壁管斜向冲击吸能特性仿真研究［J］．振动与冲击，2012，31（24）：102－107．

QI Chang，DONG Fang－liang，YANG Shu．Simulation and optimization for blast－resistant performances of a graded aluminum foam sandwich structure［J］．Journal of Vibration and Shock，2012，31（24）：102－107．（In Chinese）

［9］BAI Z，GUO H，JIANG B，etal．A study on the mean crushing strength of hexagonal multi－cell thin－walled structures［J］．Thin－Walled Structures，2014，80：38－45．

［10］JIANG B，ZHU F，JIN X，etal．Computational modeling of the crushing behavior of SKYDEX® material using homogenized material laws［J］．Composite Structures，2013，106：306－316．

［11］ROSSI A，FAWAZ Z，BEHDINAN K．Numerical simulation of the axial collapse of thin－walled polygonal section tubes［J］．Thin－Walled Structures，2005，43（10）：1646－1661．

［12］FAN Z，LU G，LIU K．Quasi－static axial compression of thinwalled tubes with different cross－sectional shapes［J］．Engi－neering Structures，2013，55：80－89．

［13］张宗华，刘树田．多边形薄壁管动态轴向冲击的耐撞性研究［C］／／2007年中国汽车工程学会年会论文集．北京：机械工业出版社，2007：437－443．

ZHANG Zong－hua，LIU Shu－tian．Crashworthiness of dynamical axial crushing of polygonal thin－walled tubes［C］／／2007SAE－China Congress Proceedings．Beijing：China Machine Press，2007：437－443．（In Chinese）

［14］白中浩，陈天志，曹立波，等．基于正交设计的汽车前纵梁吸能结构的优化［J］．汽车工程，2010，32（11）：935－939．

BAI Zhong－hao，CHEN Tian－zhi，CAO Li－bo，etal．Optimization of energy－absorbing structure of vehicle front side rail based on orthogonal design［J］．Automotive Engineering，2010，32（11）：935－939．（In Chinese）

［15］曹立波，崔崇祯，白中浩，等．八边形逐级吸能梁的设计与优化［J］．湖南大学学报：自然科学版，2010，37（1）：29－34．

CAO Li－bo，CUI Chong－zhen，BAI Zhong－hao，etal．Design and optimization of the octagonal step by step energy［J］．Journal of Hunan University：Natural Sciences，2010，37（1）：29－34．（In Chinese）

［16］JONES N．Energy－absorbing effectiveness factor［J］．International Journal of Impact Engineering，2010，37（6）：754－765．

［17］白中浩，卢静．基于多目标优化的儿童座椅匹配方法［J］．湖南大学学报：自然科学版，2013，40（3）：52－58．

BAI Zhong－hao，LU Jing．Study of matching for a child seat based on multi－objective optimization［J］．Journal of Hunan University：Natural Sciences，2013，40（3）：52－58．（In Chinese）

［18］YIN H，WEN G，HOU S，etal．Crushing analysis and multiobjective crashworthiness optimization of honeycomb－filled single and bitubular polygonal tubes［J］．Materials and Design，2011，32（8／9）：4449－4460．