Mathematical Programming Approaches for Interval Structural Behaviour and Stability Analysis

Di Wu,Wei Gao,2,Chongmin Song,Zhen Luo

Mathematical Programming Approaches for Interval Structural Behaviour and Stability Analysis

Di Wu1,Wei Gao1,2,Chongmin Song1,Zhen Luo3

Two novel mathematical programming approaches are proposed to separately assess non-deterministic behaviour and stability of engineering structures against disparate uncertainties.Within the proposed computational schemes,uncertainties attributed by the material properties,loading regimes,as well as environmental influences are simultaneously incorporated and modelled by the interval approach.The proposed mathematical programming approaches proficiently transform the uncertain structural analyses into deterministic mathematical programs.Two essential aspects of structural analysis,namely linear structural behaviour and bifurcation buckling,have been explicitly investigated.Diverse verifications have been implemented to justify the accuracy and computational efficiency of the proposed approaches through practically motivated numerical examples.

Structural behaviour;Buckling; Uncertainty;Interval analysis;Structural safety;Mathematical programming.

1 Introduction

The structural serviceability and stability are two fundamental aspects in structural analysis,which have become indispensable components in modern engineering analysis and design.Accompanied with the implementation of finite element method(FEM),the structural serviceability and stability analyses can be certainly accomplished with desirable accuracy for very complex structural systems.Indubitably,the simplicity and efficiency of FEM based computational scheme of structural analysis have stimulated the prevalent implementation in real-life engineering applications.

However,one practical issue that engineers often encounter in general practice is the discrepancy between the analytical predictions and the actual structural performance due to the impacts of uncertainties of system parameters.It is a well acknowledged phenomenon that uncertainties of system parameters are inherent,which continuously yet mercurially influence the structural performance[Gao(2006);Gao and Kessissoglou(2007);Beer and Liebscher(2008);Schuëller and Jensen(2008);Gao,Zhang,and Dai(2008);Gao,Song,and Tin-Loi,(2009);Yang and Sun(2013);Yang,Li,and Cai(2013)].Some identified typical attributions of uncertainties are including manufacturing defects,measurement and surveying errors,variational environmental factors,as well as the human induced mistakes[Melchers(1999);Gao,Wu,Song,Tin-Loi,and Li(2011);Cha and Ellingwood(2012)].These impacts of uncertainties of system parameters on the structural performance are inevitable and situational dependent,whereas simply ignoring those impacts could potentially compromise the safety of engineering structures.Therefore,it is rational and requisite to integrate deterministic structural analysis by incorporating the effects of uncertainties of system parameters.[Jiang,Han,and Liu(2008);Ma,Gao,Wriggers,Wu,and Sahraee(2010);Wu,Luo,Zhang,Zhang,and Chen(2013);Wu,Gao,Li,Tangaramvong,and Tin-Loi(2015)].

Due to the necessity of implementation of uncertainty analysis among modern engineering applications,large numbers of research works have been innovatively proposed for diverse engineering applications involving uncertainties.Among many prevalent uncertainty modellings, probabilistic/stochastic analysis framework has been extensively developed,as well as prevalently implemented across wide range of engineering disciplines[Elman,Ernst,O’Leary,and Stewart(2005);Tangaramvong,Tin-Loi,Wu,and Gao(2013);Chowdhury,Song and Gao(2014);Long,Jiang,Han,and Gao(2015)].This analysis framework encloses all methods,which have been founded upon the theory of probability and statistics[Lin and Kam(1992);Chryssanthopoulos(1998); Sadovskýa,Guedes Soaresb,and Teixeirab(2007);Loeven and Bijl(2008);Alibrandi, Impollonia,and Ricciardi(2010);Vryzidis,Stefanou,and Papadopoulos(2013)]. Another popular and commonly implemented candidate of uncertainty analysis is the fuzzy approach[Rao and Sawyer(1995);Jamison and Lodwick(2001);Zhenyu and Qiu(2001);Inuiguchi,Ramik,Tanino,and Vlach,(2003);Amrahov and Askerzade(2011);Adhikari and Khodaparast(2014)].Within fuzzy analysis framework,the theory of fuzzy sets has been pervasively implemented into engineering uncertainty analysis with some unique characteristics over the probabilistic ones[Lodwick(1990);Moens and Vandepitte(2005);Möller and Beer(2008);Amrahov and Askerzade(2010)].The third type of uncertainty analysis framework models all the uncertain system parameters by closed convex sets.Examples encompassed in this category are in-cluding the interval model[Tangaramvong,Tin-Loi,Wu,and Gao(2013);Do,Gao,Song,and Tangaramvong(2014);Tangaramvong,Wu,and Gao(2015)],Info-gap model[Ben-Haim(2010);Wu,Gao,Li,Tangaramvong,and Tin-Loi(2015)],ellipsoidal model[Kang and Luo(2010);Kang,Luo and Li(2011)],multidimensional parallelepiped model[Jiang,Zhang,Han,Liu,and Hu(2015)].One feature of the convex set approach is that the validity of the uncertainty analysis can be fulfilled without any information on the distribution function or membership function of the uncertain system parameters.Such characteristic offers extensive flexibility on the uncertainty modelling,which are very beneficial for situations where neither distribution functions nor membership functions are available due to data insufficiency [Wu,Gao,Li,Tangaramvong,and Tin-Loi(2015)].In addition to the abovementioned uncertainty analyses,there exists a relatively new framework of uncertainty analysis,known as the hybrid approach,which has been developed to conquer engineering systems involving multiple types of uncertainties.Such uncertainty analysis grants a more general and flexible framework,which has the competence to provide a unified scheme to process multiple types of uncertain system parameters[Gao,Song,and Tin-Loi(2010);Quaranta(2011);Wang,Gao,Song,and Zhang(2014);Tao,Han,Duan,and Jiang(2014);Xia,Yu,Han,and Jiang(2015)].Overall, engineering uncertainty analysis has been considerably developed for various circumstances.Among all developed engineering uncertainty analyses,the trace of a universal approach which can handle everything has not been identified yet.Therefore,it is always encouraged to develop different uncertainty analysis to satisfy various engineering demands.

In this study,two novel mathematical programming(MP)based approaches are separately proposed for analysing linear structural behaviour and stability subjected to interval discrepancies.Various uncertainties have been incorporated into the proposed computational methods,which are including material properties,loading regimes,geometric information of structural components,as well as the external influence due to the mercurial thermal effect.All uncertain system parameters are modelled as interval variables which are presumed to belong to some closed convex sets.Additional assumptions on the interrelationships within the convex sets are unnecessary,hence the proposed computational approaches are competent to deliver valid uncertainty analysis for engineering situations with excessive restraint on the availability of information of uncertain parameters.Furthermore,by introducing alternative formulations for the structural linear behaviour and stability analysis,the corresponding uncertain system of linear equations and eigenvalue problems are able to be explicitly transformed into deterministic nonlinear mathematical programming(NLP)problems with interval parameters being treated as bounded optimization variables.Such implementation of reformulation eliminates all possible interval arithmetic within the analysis framework.Consequently,the interference on the sharpness of results due to the issue of interval dependency[Muhanna,Mullen,and Zhang(2005)]can be completely eliminated.Besides the improvement of the sharpness of the computational results,the proposed computational approach is able to retrieve the information on the critical values of uncertain parameters that are corresponding to the extremities of the structural output at vacuum of computational cost.Even though the identification of critical values for uncertain parameters seems trivial,the contribution of such information becomes noticeable when the structure is designed with the consideration of uncertainties.In addition,the proposed MP approaches offer a computational efficient analysis framework by merely calculating the extremities of the structural outputs.All mathematical programs involved take the format of standard NLPs,such that it provides a non-enumerative computational approach which delivers bounded convex sets for the structural output within two calculations(i.e.,one for the upper bound determination,and the other one for lower bound determination).Since all proposed computational approaches are formulated within the framework of FEM,it has potential to be integrated into commonly utilized FEM software.

This paper has been organized into the following formation.In Section 2,the linear structural behaviour with various interval uncertainties are investigated,and then the first proposed MP approach is presented to assess the robustness of serviceability of engineering structures.In Section 3,the second MP approach is derived to evaluate the stability of engineering structure with consideration of various uncertain effects.In order to illustrate the applicability,accuracy,as well as the computational efficiency of the proposed MP approaches,four numerical examples(including two trusses and two frames)have been selected and investigated in Section 4.For all the academic sized structures,analytical solutions on the closed convex sets of the targeting structural output have been determined for the purpose of results verification,whereas Monte Carlo simulation(MCS)approach is adopted for partial verification and evaluation of computational efficiency of the proposed approaches through practically motivated numerical examples.Finally,conclusions are summarised in Section 5.

2 Linear structural behaviour analysis with consideration of interval uncertainties

In this section,the first MP approach is introduced for assessing the bounded structural responses of 2-dimensional (2D) truss and frame involving various interval parameters.The proposed MP approach utilizes an alternative FE formulation,such that the interval linear structural behaviour analysis is reformulated into deterministic NLPs with all interval parameters being modelled as MP variables.The first advantage of the proposed MP approach is that the inveterate interference on the sharpness of the bounded structural responses due to interval dependency is completely excluded by circumventing the implementation of interval arithmetic.Unlike other enumerative or simulative schemes,the proposed MP approach is able to deliver the upper and lower bounds of any particular structural displacement within two independent calculations.Thus,the proposed MP approach has considerable computational efficiency which can be further demonstrated through the numerical examples presented in Section 5.

Throughout this study,the accounted uncertain system parameters are including,the material properties of structural element(i.e.,Young’s modulus,,and coefficient of thermal expansion,),geometry of structural element(i.e.,cross-sectional area,,and second moment of area of beam element),loading regimes(i.e.,the externally applied loads,),as well as the uncertain thermal effects due to change of temperature(i.e.,Δ).

All uncertain system parameters are modelled as interval variables which are bounded by some closed convex sets.This particular uncertainty modelling is often encountered in engineering situations where probabilistic or fuzzy approaches cannot be confidently employed due to insufficiency of information to obtain the distribution or membership functions.As an illustration,the uncertain Young’s modulus of a structure withnindependent structural elements can be modelled as:

Figure 1:2D truss element for structural behaviour analysis(a)generalized stress and(b)generalized strain.

2.1 Structural behaviour analysis of 2-dimensional truss with interval uncertainties

For interval structural analysis,an alternative FE formulation is adopted.The adopted 2D truss element involves one independent degree-of-freedom[Maier(1970)],which is illustrated in Figure 1.

By considering the thermal effects,the three governing equations,namely equilibrium,compatibility,and constitutive equations for 2D truss elementican be respectively expressed as:

Alternatively,Eqs.(2)–(4)have abbreviations as:

where Cidenotes the elemental compatibility matrix,and its transpose denotes the elemental equilibrium matrix;denotes the thermal load matrix which is implemented to account the thermal effects;Fidenotes the applied load vector atith element;Sidenotes stiffness matrix of theith element;αi∈ ℜ denotes the coefficient of thermal expansion(C.T.E)of theith element;ΔTi∈ ℜ denotes the change of temperature experienced by theith element;θ denotes the inclination angle of elementi;andEi,Ai∈ ℜ denote the Young’s modulus and cross-sectional area of theith element.

By assembling the three governing equations for the entire truss structure,the global form of the three governing equations of any 2D truss structure withnelements andddegree-of-freedoms can be obtained which can be expressed as:

where C∈ℜn×ddenotes the global compatibility matrix,and its transpose denotes the global equilibrium matrix;∈ℜn×ndenotes the global stiffness matrix of 2D truss structure;denotes theith component of the global thermal force vec-denotes the externally applied loads;u∈ℜddenotes the global displacement vector;q,e∈ℜndenote the generalized stress and strain of 2D truss structure respectively.

Eqs.(8)–(10)provide an alternative,yet equivalent formulation to the structural behaviour analysis considering thermal effects using traditional FEM(i.e.,the traditional FEM uses 2D bar element which has four degree-of-freedoms at each 2D bar element).The detailed proof of the equivalency of formulations between two approaches is presented in Appendix A.

Therefore,by implementing abovementioned new FE formulation, the interval structural behaviour analysis subjected to various uncertain system parameters can be formulated into two explicit NLPs for the upper and lower bounds of the displacement of any specific degree-of-freedom.

In specific,the upper bound of a particular degree-of-freedomup(for 1≤p≤d)can be formulated as:

whereas the lower bound is formulated as:

where d∈ℜddenotes a location vector which has the form of:

By solving Eqs.(11)and(12),the upper and lower bounds of thepth degree-of freedom of any 2D truss structure involving interval uncertainties can be obtained.

2.2 Structural behaviour analysis of 2-dimensional frame with interval uncertainties

For the case of 2D frame element,the adopted FE formulation involves three independent degree-of-freedoms[Maier(1970)],which can be illustrated in Figure 2.

Figure 2:2D frame element for structural behaviour analysis(a)generalized stresses and(b)generalized strains.

Basing on the adopted FE model,the three governing equations,namely equilibrium,compatibility,and constitutive equation,for a generic 2D frame elementican be expressed respectively as:

whereIi∈ℜ denotes the second moment of area of theith frame element.Introducing the abbreviations,Eqs.(14)–(16)can be alternatively expressed as:

Therefore,by assembling contributions from each element presented in the 2D frame structure,the global governing equations for linear behaviour of 2D frame involvingnelements andddegree-of-freedoms can be expressed as:

However,from Eq.(16),it can be observed that the axial component of the generalized stress of any 2D frame elementiis independent of the rotational components.Thus,Eq.(16)can be further decomposed into:

and

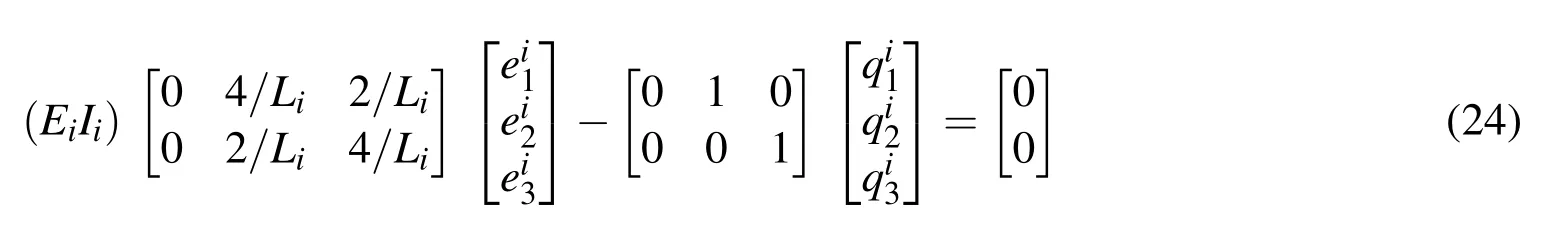
which have abbreviations as:

and

Furthermore,by assembling contributions from allnelements,the corresponding global formulations of Eqs.(25)and(26)can be expressed respectively as:

where Sai∈ ℜn×3nis theith component of the global axial stiffness Sa(i.e.,wheni=k,for 1≤k≤n,Sak(k,3k−2:3k)=,and rest of the components are zeroes);Sri∈ ℜ2n×3nis theith component of the global flexural stiffness matrix Sr(i.e.,wheni=k,for 1≤k≤n,Srk(2k−1:2k,3k−2:3k)=,and rest of the components are zeroes);Ta∈ℜn×3nis the transition matrix which extracts out all the axial generalized stresses from the global generalized stress vector;and Tr∈ ℜ2n×3nis the transition matrix which extracts out all the end rotational generalized stresses from the global generalized stress vector.

By implementing this alternative FE formulation,the interval behaviour of 2D frame structure against various uncertainties can be formulated into two independent NLPs for calculating the upper and lower bounds of the displacement.The NLP corresponding to the upper bound calculation is:

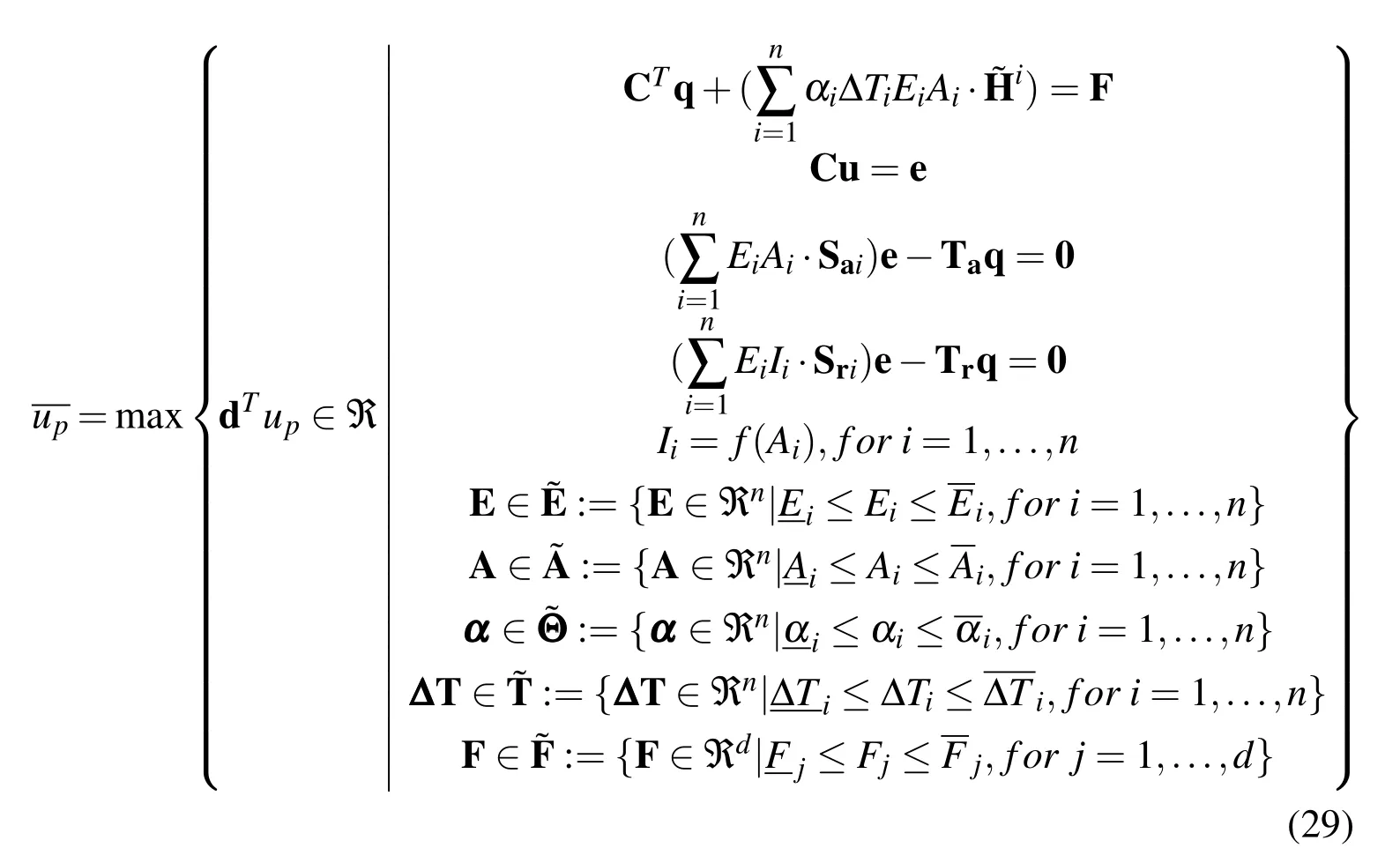
and the lower bound calculation can be expressed as:

wheref(·)denotes physical compatibility reinforcement function.In this case,it maintains the physical compatibility between cross-sectional area and the secondmoment of area of the same beam element.

Eqs.(11),(12),(29),and(30)de fine the feasible regions for the upper and lower bounds of the displacement of thepth degree-of-freedom of 2D truss and frame structure respectively.By adopting the alternative FE formulation,all interval system parameters are treated as MP variables with corresponding upper and lower bounds.Thus,the interval structural behaviour analysis of truss and frame structure can be efficiently executed by solving two pairs of NLPs.In addition,since all interval parameters are modelled as MP variables,the implementation of interval arithmetic is completely obviated such that,the sharpness of the obtained bounds of displacement can be further enhanced.Moreover,the proposed MP approach is capable to strictly maintain the existing physical compatibility between any interacted parameters.In Eqs.(29)and(30),the compatibility function has been introduced to reinforce the interrelationship between the cross-sectional area and the second moment of area of the same structural element(i.e.,Ii=f(Ai),for i=1,...,n).Thus,the bounds of the displacement determined by the MP approach are also the physically feasible solutions.

3 Linear structural stability analysis with consideration of interval uncertainties

In this section,a novel MP approach is proposed for linear stability/bifurcation buckling analysis of 2D truss and frame structure involving interval system parameters with variational thermal effects.

3.1 Structural stability analysis of 2-dimensional truss with interval uncertainties

For second-order geometrically nonlinear analysis formulated through traditional FEM,the total strain in the direction of theith truss element axis is a nonlinear function,which has been de fines as[Przemieniecki(1985)]:

where

andLidenotes the length of theith 2D truss element;andforj=1,...,4 denotes the degree-of-freedoms associated with the considered element.

In this study,the variational thermal effect is considered accompanied with other uncertainties,such that the elastic strain εxxand the thermal strain εTof truss elementihave the relationship as:

Therefore,the potential energy of theith member can be determined as:

By neglecting the higher-order term,and then introducing:

wheredenotes the axial force of elementi.The governing equation for the second order geometrically nonlinear analysis of theith element can be formulated by using the Castigliano’s theorem(Part I)[Przemieniecki(1985)],which can be expressed as:

or the abbreviation is:

Therefore,the deterministic global governing equation for 2D truss structure withddegree-of-freedoms andnelements can be formulated by assembling across all elemental contributions,which can be expressed as:

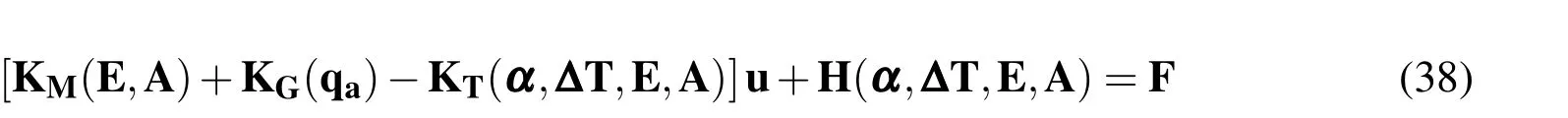
where λcr∈ ℜ denotes the linear bifurcation buckling load factor,which is the minimum positive eigenvalue of Eq.(39);whereas δu ∈ ℜddenotes the eigenvector that is corresponding to the linear bifurcation buckling load factor.Since δu is indeterminate in linear bifurcation buckling analysis,it de fines the buckling shape of the structure instead of actual buckling displacement[Cook,Malkus, Plesha,and Witt(2002)].

When the uncertainties of system parameters are considered in the linear stability analysis,all stiffness matrices in Eq.(39)are transformed into non-deterministic format,and the stability analysis is extended into interval eigenvalue problem.However,interval linear bifurcation buckling analysis through traditional FE formulation involves computational obstacles which inhibit its computational tractability.In the deterministic structural linear bifurcation buckling analysis through traditional FEM,it involves a two-phase calculation for determining the final linear bifurcation buckling load factor. In the first phase of the analysis, a linear analysis is performed in prior for calculating the internal axial force of each structural element at the reference loading condition.Basing on the determined internal axial force,the geometric stiffness matrix of the structure can be formulated and the eigenvalue problem can be executed in the second phase.However,when interval uncertainties are considered in the analysis,the first computational issue is to find an adequate scheme to solve the two-phase calculation involved in structural linear bifurcation buckling analysis,whereas the second issue is to maintain physical compatibilities of all uncertain parameters between two phases of the analysis.

In order to fulfil the purpose of robust assessment of structural stability with considerations of uncertain parameters,an adequate MP approach is proposed for interval structural stability assessment,which implements an alternative FE discretization to combine the two phases of the stability analysis into a single calculation.

The adopted FE model of the 2D truss for the second-order geometrically nonlinear analysis is depicted in Figure 3[Maier(1970)].

Figure3:Generic 2D truss elementifor second-order geometrically nonlinear analysis(a)generalized stresses,(b)generalized strains.

For the generic 2D truss elementishown in Figure 3,the equilibrium condition can be formulated as:

with the abbreviation:

The compatibility conditions can be formulated as:

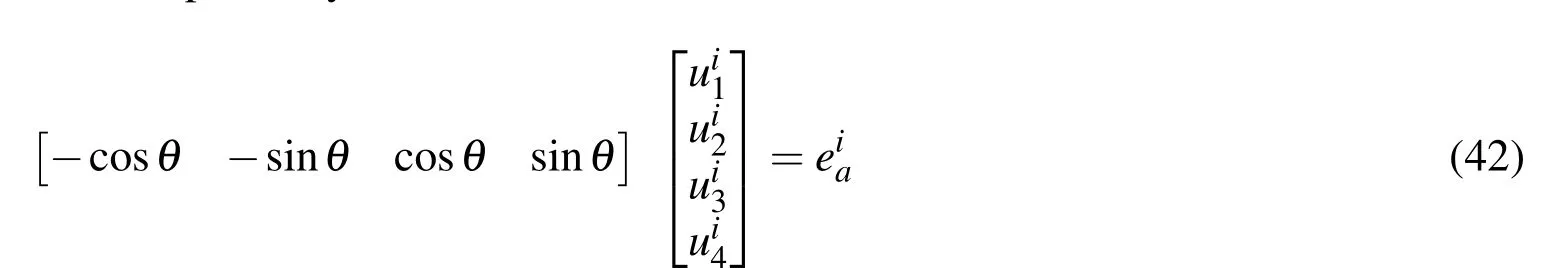
with the abbreviations:

The constitutive conditions can be expressed as:

with abbreviations as:

From Eqs.(46)–(49),it can be observed that

Eqs.(40)–(49)form the governing equations for second-order geometrically nonlinear analysis of 2D truss element through an alternative FE formulation.The newly adopted FE formulation is equivalent to the traditional FEM approach.The proof of this equivalency of formulation is illustrated in Appendix B.

From Appendix B,it is noticed that the material,geometric,and thermal stiffness matrix of 2D truss elementican be decomposed into several components.Thus,by extending this notion,the global material,geometric,as well as thermal stiffness matrix can be decomposed,such that the eigenvalue problem defined in Eq.(39)can be reformulated as:

where C0∈ ℜn×ddenotes a global compatibility matrix of the 2D truss,and its transpose represents the global equilibrium matrix;Cg∈ ℜn×dis the global compatibility matrix which represents the relation between the generalized strain in the transverse direction with the global displacement,and its transpose represents the second equilibrium matrix;Sm,Sg,St∈ ℜn×nare the stiffness matrices for the axial,transverse,and thermal components calculated in the reference con figuration,respectively.Due to the diagonal structures of matrices Sm,Sg,and St,Sm,Sgand Stcan be alternatively expressed as

Furthermore,by implementing the decomposition presented in Eq.(50),the lower bound of the buckling load factor(i.e.,)of 2D truss with interval uncertainties can be formulated as:

3.2 Structural stability analysis of 2-dimensional frame with interval uncertainties

For linear structural stability analysis of 2D frame,the adopted FE model of the frame element is depicted in Figure 4[Maier(1970)].

Figure 4:Generic 2D frame element i for second-order geometrically nonlinear analysis(a)generalized stresses,(b)generalized strains.

By implementing the alternative FE model,the equilibrium equation for theith beam is expressed as:

with abbreviation as:

The compatibility equations are formulated as:

which have abbreviations as:

and the constitutive equations are formulated as:

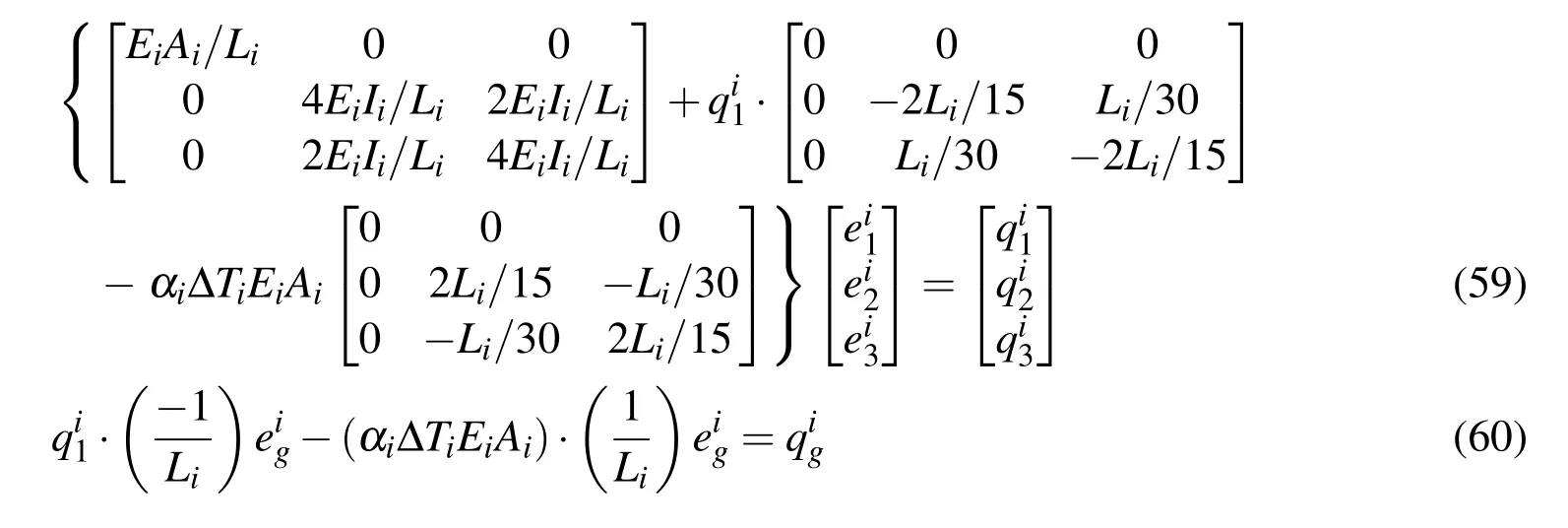
with abbreviations as:

Eqs.(53)–(62)present governing equations for the second order geometrically nonlinear analysis of 2D frame through an alternative FE model.The adopted FE formulation in this study is equivalent to the traditional FEM but with additional computational advantages.The proof of the equivalency between two approaches is presented in Appendix C.

Furthermore,by implementing the notion of decomposition presented in Eq.(50)once again,the lower bound of the linear bifurcation buckling load factorof 2D frame structure involving interval uncertainties can be formulated as:where C0∈ ℜ3n×dand Cg∈ ℜn×ddenote the two compatibility matrices and their transposes denote the equilibrium matrices;∈ℜ3n×3ndenotestheithcomponent ofsuch that:

On the other hand,the upper bound of the linear bifurcation buckling load factor of 2D frame involving interval uncertainties can be formulated as:

Eqs.(51),(52),(63)and(66)explicitly formulate the feasible regions for the lower and upper bounds of the linear bifurcation buckling load factor of 2D truss and frame with considerations of various uncertainties respectively.Unconventional FE models for second order geometrically nonlinear analysis have been adopted for truss and frame.Such alternatives are able to reformulate the interval eigenvalue analysis into standard NLPs with all interval uncertainties are being modelled as optimization variables.The proposed MP approach combines a two-phase buckling analysis into a single calculation such that the compatibilities of all interval parameters are rigorously controlled throughout entire analysis.Thus,the obtained computational results are always corresponding to a set of physically existing uncertain parameters.In addition,since no interval arithmetic is involved,the sharpness of the bounds of the buckling loads is further appreciated by obviating the overestimation due to the issue of interval dependency.Unlike enumerative or simulative approaches,the proposed method is able to determine the lower and upper bounds of the buckling load of 2D structures within two explicit calculations(i.e.,one for lower bound and the other one for upper bound).

4 Numerical examples

In order to demonstrate the applicability,accuracy,as well as the computational efficiency,numbers of numerical examples have been investigated in this section.For linear structural behaviour analysis,two 2D trusses have been investigated.The first example involves a simple truss in which the accuracy of the proposed MP approach is justified by comparing the bounds of displacement with the analytical solutions.Then,the proposed MP approach is employed to determine the bounds of displacements of a more complex truss structure which is presented in Example 2.Due to the lack of analytical solutions for complex truss structure,the Monte-Carlo simulation(MCS)method is adopted for results verification for some selected degrees-of-freedom.In Example 3,the linear stability of a classical fixed-pined column involving various interval uncertainties is investigated using the proposed MP approach.Furthermore,by comparing with the analytical solution of such classical example,the accuracy and capability of the proposed MP approach is clearly evidenced.Finally,a practically motivated 2D frame structure is investigated to further demonstrate the applicability and efficiency of the proposed method.Once again,the MCS approach is implemented for the purpose of accuracy and efficiency comparisons.

For both structural linear behaviour and stability analysis,the upper and lower bounds of various structural outputs(i.e.,structural displacements from linear behaviour analysis,buckling load factor from linear bifurcation buckling analysis)are taken format of standard NLPs.Thus all NLPs involved in this study are computationally solved by a prevalent yet efficient NLP solver,namely CONOPT[Drud(1994)],which is operated under the framework of The General Algebraic Modeling System(GAMS)[Brooke,Kendrick,Meeraus,and Raman(1998)].CONOPT is a feasible path solver which has been developed basing on the GRG(Generalized Reduced Gradient)method and is able to conquer large and sparse NLP models.

4.1 Example 1:simple two-bar truss

In Example 1,a simple two-bar truss is considered which suffers various uncertain conditions.The structural layout of the investigated truss is presented in Figure 5.

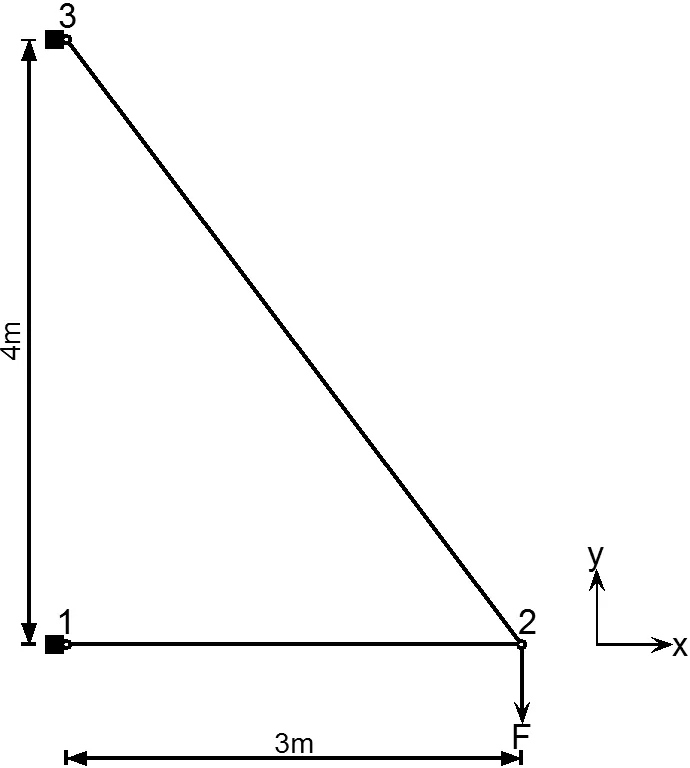
Figure 5:Example 1:simple two-bar truss.

In this example,various uncertain parameters have been considered which are including Young’s modulus,cross-sectional area,magnitude of the applied load,change of temperature,as well as the coefficient of thermal expansion of each bar.The detailed information of all accounted interval parameters is presented in Table 1.

By implementing the proposed MP approach for linear structural behaviour analysis,the lower(i.e.,by solving Eq.(12))and upper bounds(i.e.,by solving Eq.(11))of the horizontal displacement of Node 2(u2x)are=−4.054×10−2mand=−1.993×10−2mrespectively.Moreover,the lower and upper bounds of the vertical displacement of node 2(u2y)determined by the MP approach are=−0.169mand=−8.235×10−2mrespectively.In addition,analyti-cal solutions for both displacements of node 2 are determined through the FEM for the purpose of result verification.By implementing the FEM,the horizontal and vertical displacement of node 2 can be formulated as:

Table 1:Information of interval parameters for Example 1.

Therefore,by implementing Eqs.(67)and(68),the analytical solutions(AS)of the bounds of both displacements are determined such that=−8.235×10−2m.It is evidently illustrated that identical results are obtained from both approaches,therefore the proposed MP approach accurately capture the extremities of displacements in this case.

In addition to the delivery of the extremities of structural behaviour against various uncertainties,the proposed MP approach is also able to provide the information on the uncertain parameters that are causing such extreme responses.In this particular instance,critical information that is causing the extreme responses of displacements is summarized in Table 2.

Table 2:Critical values of uncertain parameters for extreme structural behaviour of Example 1.

From Table 2,it can be observed that all uncertain parameters corresponding to the extreme structural behaviour are also taking combinations of their corresponding bounds.There are two important facts can be concluded from Table 2.The first key point is that for the same degree-of-freedom,the uncertain parameters corresponding to the lower bound are not necessarily opposite in extremities to the uncertain parameters causing the upper bound.The second key point is that the upper(or lower)bounds of the structural behaviours do not necessarily have the same set of uncertain parameters.

4.2 Example 2:four by four truss structure

The second example investigated is a four-by-four truss which is subjected to a loading regime as shown in Figure 6.Once again,all uncertain parameters considered in Example 1 are also adopted in Example 2.The information of all uncertain parameters considered in Example 2 is presented in Table 3.

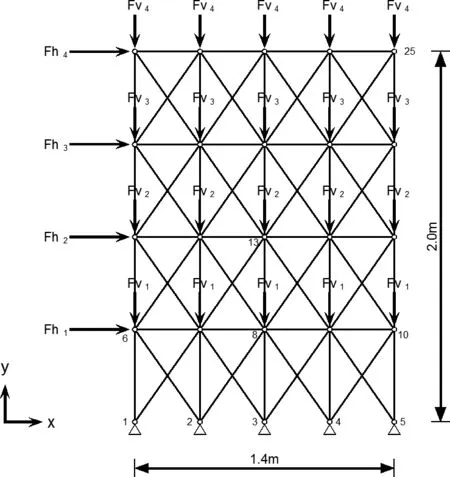
Figure 6:Example 2:four-by-four truss.

In order to further demonstrate the applicability of the proposed MP approach for interval structural behaviour analysis,the horizontal and vertical displacements of some selected nodes of the truss have been presented in Table 4(i.e.,the selected nodes are 13,21,and 25).Furthermore,since determining analytical solutions of displacements for such truss structure is impractical,the MCS approach is implemented for the purpose of results verification to a certain extent.For the MCS approach,10 million simulations have been performed and the computational results are also reported in Table 4.

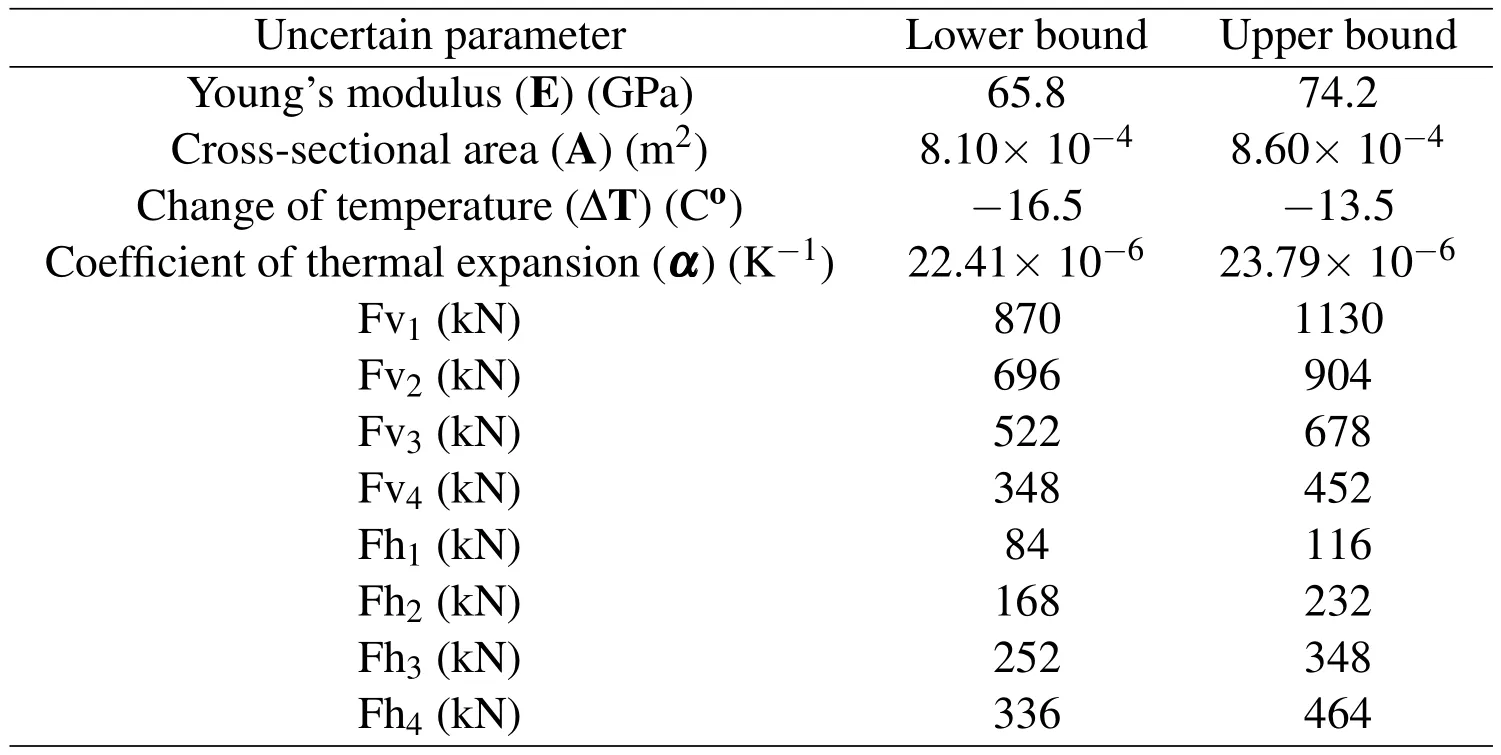
Table 3:Information of interval parameters for Example 2.

Table 4:Interval structural behaviour at some selected locations.

From Table 4,it is clearly illustrated that all bounds of structural behaviour calculated by the MCS approach are enclosed within by the intervals reported by the proposed approach(i.e.,the MP approach is able to provide inferior lower bound and superior upper bound).Therefore,it is evidenced that the performance of the MP approach surpasses the achievement of the MCS approach with high simulation numbers.It should be noted that the simulation times depend on the complexity of the problem.In general,increasing simulation times is the way to produce more accurate results.Realistically,exact solutions are impossible to be achieved by MCS for practical engineering applications,although which might be obtained by in finite simulations.

In order to further demonstrate the applicability of the proposed MP approach,some numerical experiments have been conducted to investigate effects due to various uncertain conditions on the structural behaviours.The first numerical experiment is a sensitivity analysis for investigating the variations ofu25,y,which is the vertical displacement of Node 25,against the interaction between the change ratios of coefficient of thermal expansion and change of temperature.By implementing the proposed MP approach,the variational structural behaviour pro files(i.e.,one for lower bound and one for upper bound)for vertical displacement at Node 25 can be constructed as in Figure 7(a)and(b):

From Figure 7(a)and(b),it can be observed that both upper and lower bound response surfaces are monotonic within the investigated range.Furthermore,a second numerical experiment is also conducted to investigate the various uncertain effects on the structural behaviour due to different uncertain scenarios.For the second numerical experiment,only one uncertain parameter is varying at a time.The results of the second investigation are illustrated in Figure 8.

From Figure 8,it can be observed that before change ratio reaches to 0.16,the effects of uncertain force has the most influence on the vertical displacement of Node 25.However,when the change ratio is greater than 0.16,Young’s modulus starts to influence the lower bound of displacement more than the uncertain force does.Also,it is observed that the concerned displacement is not linearly proportional to the change ratio of all considered interval parameters.The exception comes from the Young’s modulus.That is,the interrelationship between the bounds of concerned displacement and the width of interval Young’s modulus is nonlinear.Thus,linear scaling is not applicable for engineering situations when there is an alternation on the change ratio of Young’s modulus,which indicates the necessity of performing separate calculations.

4.3 Example 3: fixed-pined column

The third example is a fixed-pinned column which is implemented for the interval linear bifurcation buckling analysis.The general structural layout of the considered column is shown in Figure 9.

The investigated column is a 310UB46.2 beam[OneSteel(2000)]with a length of 2m.For interval linear bifurcation buckling analysis of the fixed-pinned column,three cases with distinctive uncertain conditions have been investigated in this example to demonstrate the applicability and accuracy of the proposed method.The information of all interval parameters considered in the three cases are summarized in Table 5.

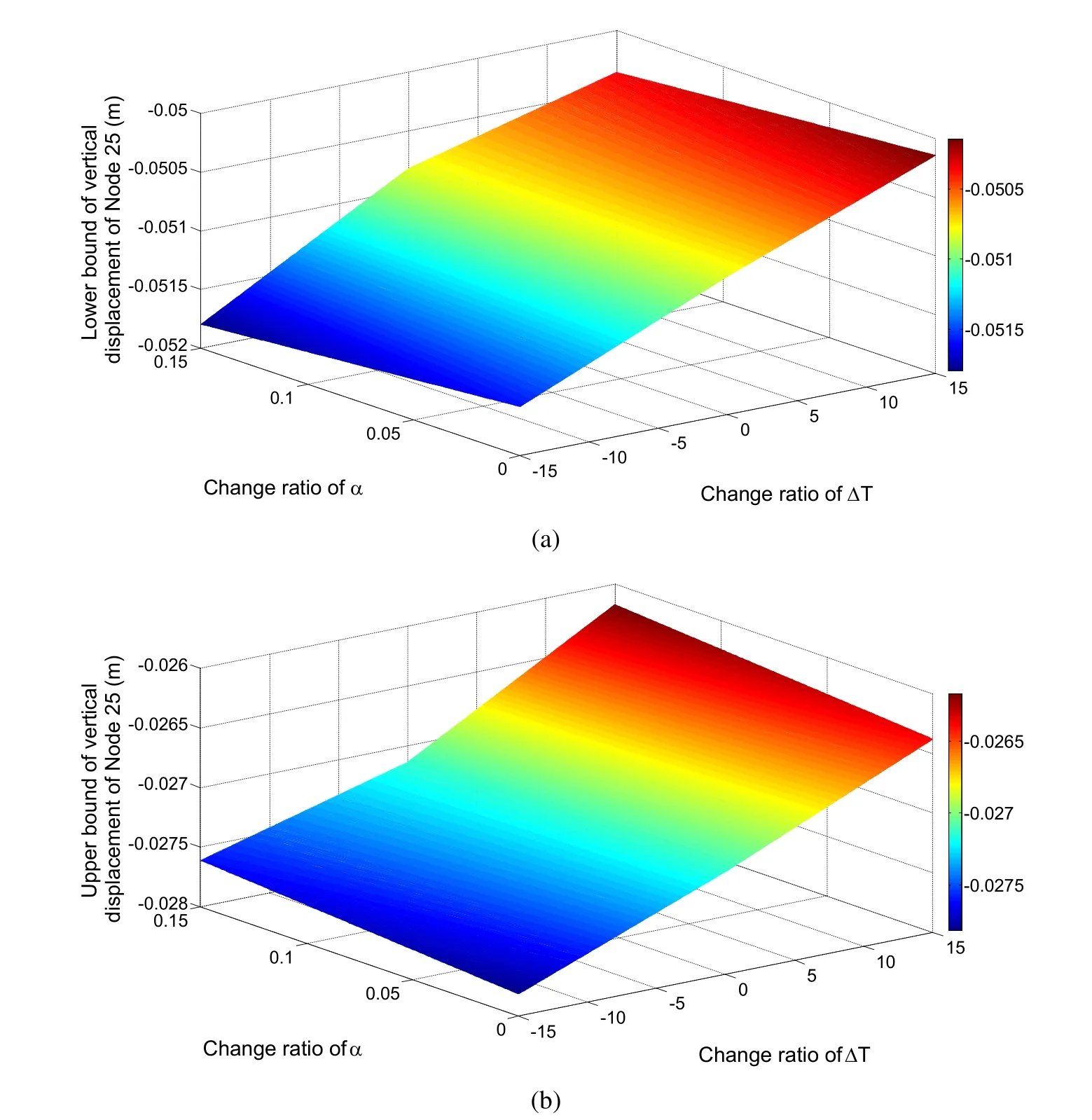
Figure 7:Response surface for(a)lower bound and(b)upper bound of vertical displacement of Node 25.

Table 5:Information of the three uncertain situations for Example 3.

Figure 8:Various uncertain effects on vertical displacement of Node 25.

Figure 9:Example 3: fixed-pinned column.

In addition,since the second moment of area of the column is a function of its cross-sectional area.Therefore,the following equation is introduced to maintain the physical compatibility between these two uncertain yet correlated parameters.

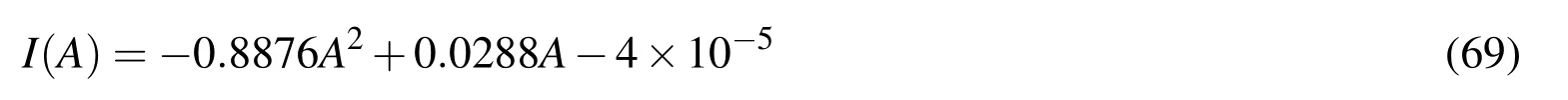
Eq.(69)is obtained by plotting the second moment of inertia of all the universal beams under the 310UB series manufactured by OneSteel Limited against their corresponding cross-sectional areas[OneSteel(2000)].

By employing the proposed MP approach,the lower and upper bounds of the linear bifurcation buckling load factor are calculated and summarized in Table 6.In order to verify the accuracy of all computational results obtained from the proposedmethod,analytical solutions of the bounds of buckling load factor can be derived from the deterministic formulation.Using the classical theory of buckling,the buckling load factor of the fixed-pinned column with the consideration of thermal effect can be formulated as:

Table 6:Bounds of linear bifurcation buckling load factors of Example 3.

From Table 6,it is quite noticeable that for all three investigated cases,the bounds of buckling load factors obtained from MP approach completely agree with the analytical solutions.Therefore,from this example,the accuracy and applicability of the proposed MP approach for interval linear bifurcation buckling analysis of fixed-pinned column with considerations of uncertain system parameters have been evidently justified.

4.4 Example 4: five-bay ten-storey frame structure

For the fourth example,a practically motivated example is presented in Figure 10,which involves a five-bay ten-storey frame structure.

In this particular example,the considered uncertain parameters are including the Young’s moduli,coefficient of thermal expansions,cross-sectional areas of beams and columns,loading regimes,as well as the change of temperatures.In this frame,all columns are 400WC270 whereas all beams are modelled as 310UB46.2.From Example 3,it is emphasized that the compatibility between the cross-sectional area and the second moment of area of the same element must be thoroughly reinforced.Therefore,the sectional compatibility function for all columns is:

whereas all the beams have the compatibility function as:

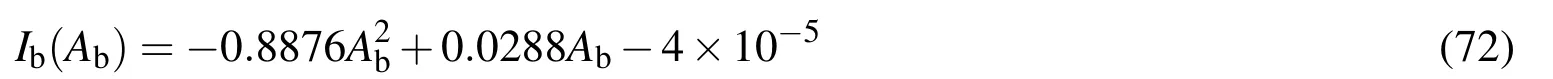
Once again,three circumstances,each with distinctive uncertain conditions,have been investigated.The information of uncertain parameters considered in all three cases is presented in Table 7.

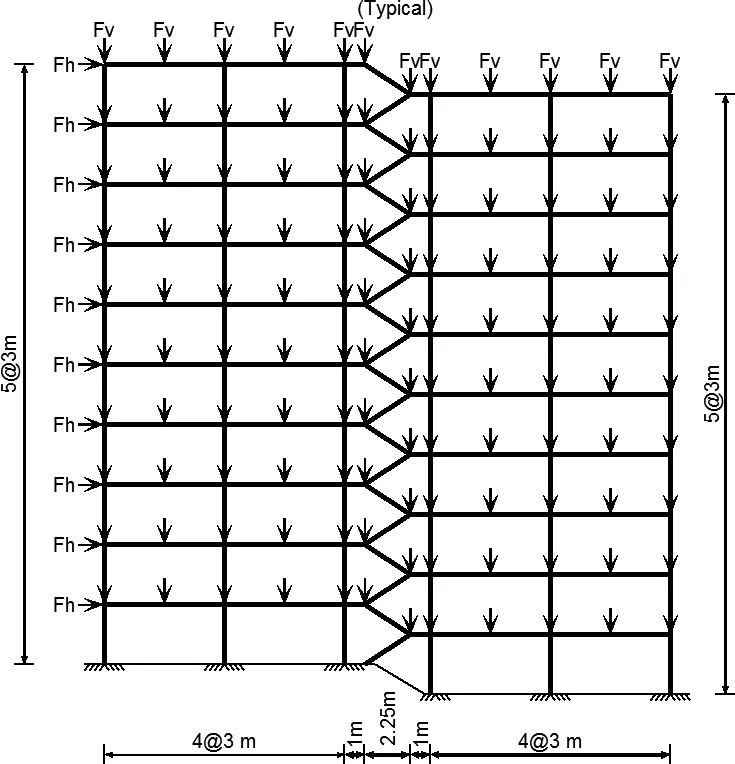
Figure 10:Example 4 Five-bay ten-storey frame.

Table 7:Information of uncertain parameters of Example 4.

By utilizing the proposed MP approach for interval structural stability analysis,upper and lower bounds of the buckling load factors for all three cases can be calculated with noticeable computational effort.In addition to the MP approach,the MCS approach with 1 million simulations is also employed to verify the results to a certain extent. The computational results on the bounds of buckling load factors of all three cases are reported in Table 8.

In addition to the calculations on the bounds of buckling load factors,the com-putational consumption(i.e.,CPU time)for all three cases between two different methods have also been recorded in Table 9.The computer implemented to perform all reported computational results has processor of InterlⓇCore™i7-4770 CPU@3.40GHz,and memory of 16.0 GB.All reported computational times below have unit of second.

Table 8:Bounds of buckling load factors of Example 4.

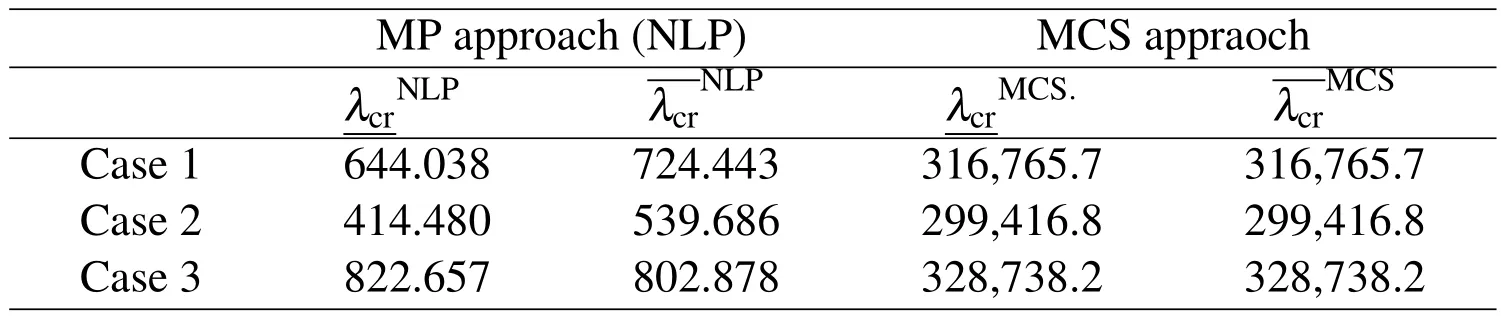
Table 9:Computational time for Example 4.

As clearly indicated in Table 8,the bounds of buckling load factors of the five-bay ten-storey frame calculated by the MP approach enclose all the results computed from the MCS approach with 1 million simulations for all three investigated cases.Therefore,the performance of the proposed MP approach surpasses the MCS approach with high simulation numbers.Furthermore,from Table 9,it can be observed that the computational effort consumed by the MP approach is much less than the MCS approach.On average,the MCS with 1 million simulations would require 314,973.6 seconds(or 3.65 days)to accomplish one interval structural stability analysis(i.e.,determinations for lower and upper bounds of buckling load factor accounted as one complete analysis),whereas the MP approach would only consume 1316.1 seconds.Therefore,the proposed MP approach has the competence to deliver sharper intervals for buckling load factors of structures involving interval uncertainties with considerable computational efficiency.

5 Conclusion

Two mathematical programming approaches have been proposed explicitly for interval linear structural behaviour and stability analysis with the considerations of diverse uncertain parameters.By adopting the alternative FE modelling,both interval structural behaviour and stability analysis are reformulated into deterministic nonlinear programming problems with all interval parameters are being modelled as bounded variables.Such reformulation alleviates the dependence issue caused by interval arithmetic,thus the sharpness of the results can be comprehensively enhanced.All calculations of the lower and upper bounds of targeted structural outputs take the format of standard nonlinear programs,so the calculations can be executed by any standard nonlinear programming solvers.

Unlike traditional uncertainty analysis,the proposed approaches are able to offer the information on the uncertain parameters that are devoting the extreme structural output at zero computational cost.Such sensitive information becomes compellingly valuable for engineers in structural design and system retro fitting.

Four numerical examples have been meticulously selected to demonstrate the various aspects of the proposed approaches.By diversely investigating those examples,the applicability, accuracy, as well as the computational efficacy of the proposed approaches have been robustly justified.Due to the simplicity of formulation,noticeable computational efficiency,as well as high quality of solutions,the proposed two mathematical programming approaches can be integrated into modern engineering applications.

For interval linear structural stability analysis,only general types of structures are considered.However,some unusual instances,which are including linear bifurcation buckling analysis of structures with repeated eigenvalues,closely spaced eigenvalues,as well as defective structures,have not been considered in the present study.Further explorations are necessary for abovementioned special circumstances.

Acknowledgement:This research work has been supported by Australian Research Council through Discovery Projects DP130102934 and DP140101887.

Adhikari,S.;Khodaparast,H.H.(2014):A spectral approach for fuzzy uncertainty propagation in finite element analysis.Fuzzy Sets and Systems,vol.243,pp.1–24.

Alibrandi,U.;Impollonia,N.;Ricciardi,G.(2010):Probabilistic eigenvalue buckling analysis solved through the ratio of polynomial response surface.Computer Methods in Applied Mechanics and Engineering,vol.199,pp.450–464.

Amrahov,¸S.E.;Askerzade,I.N.(2010):Fuzzy optimization of multivariable fuzzy functions.CMES-Computer Modeling in Engineering and Sciences,vol.70,pp.1–9.

Amrahov,¸S.E.;Askerzade,I.N.(2011):Strong solutions of the fuzzy linear systems.CMES-Computer Modeling in Engineering and Sciences,vol.76,pp.207–216.

Beer,M.;Liebscher,M.(2008):Designing robust structures–A nonlinear simulation based approach.Computers&Structures,vol.86,pp.1102–1122.

Ben-Haim,Y.(2010):Info-Gap Economics:An Operational Introduction,Palgrave-Macmillan.

Brooke,A.;Kendrick,D.;Meeraus,A.;Raman,R.(1998):GAMS:A User’s Guide.Washington DC:GAMS Development Corporation.

Cha,E.J.;Ellingwood,B.R.(2012):Risk-averse decision-making for civil infrastructure exposed to low-probability,high-consequence events.Reliability Engineering&System Safety,vol.104,pp.27–35.

Chowdhury,M.S.;Song,C.;Gao,W.(2014):Shape sensitivity analysis of stress intensity factors by the scaled boundary finite element method.Engineering Fracture Mechanics,vol.116,pp.13–30.

Chryssanthopoulos,M.K.(1998):Probabilistic buckling analysis of plates and shells.Thin-Walled Structures,vol.30,pp.135-157.

Cook,R.D.;Malkus,D.S.;Plesha,M.E.;Witt,R.J.(2002):Concepts and application of finite element analysis,4th Edition.United States:John Wiley&Sons Inc.

Do,D.M.;Gao,W.;Song,C.;Tangaramvong,S.(2014):Dynamic analysis and reliability assessment of structures with uncertain-but-bounded parameters under stochastic process excitations.Reliability Engineering and System Safety,vol.132,pp.46–59.

Drud,A.S.(1994):CONOPT-a large-scale GRG code.ORSA Journal on Computing,vol.6,pp.207–216.

Elman,H.C.;Ernst,O.G.;O’Leary,D.P.;Stewart,M.(2005):Efficient algorithms for the stochastic finite element method with application to acoustic scattering.Computer Methods in Applied Mechanics and Engineering,vol.194,pp.1037–1055.

Gao,W.(2006):Stochastically optimal active control of a smart truss structure under stationary random excitation.Journal of Sound and Vibration,vol.290,pp.1256–1268.

Gao,W.;Kessissoglou,N.J.(2007):Dynamic response analysis of stochastic truss structures under non-stationary random excitation using the random factor method.Computer Methods in Applied Mechanics and Engineering,vol.196,pp.2765–2773.

Gao,W.;Zhang,N.;Dai,J.(2008):A stochastic quarter-car model for dynamic analysis of vehicles with uncertain parameters.Vehicle System Dynamics,vol.46,pp.1159–1169.

Gao,W.;Song,C.;Tin-Loi,F.(2009):Probabilistic interval response and reliability analysis of structures with a mixture of random and interval properties.CMES-Computer Modeling in Engineering and Sciences,vol.46,pp.151–189.

Gao,W.;Song,C.;Tin-Loi,F.(2010):Probabilistic interval analysis for structures with uncertainty.Structural Safety,vol.32,pp.191–199.

Gao,W.;Wu,D.;Song,C.;Tin-Loi,F.;Li,X.(2011):Hybrid probabilistic interval analysis of bar structures with uncertainty using a mixed perturbation Monte-Carlo method.Finite Elements in Analysis and Design,vol.47,pp.643–652.

Inuiguchi,M.;Ramik,J.;Tanino,T.;Vlach,M.(2003):Satisficing solutions and duality in interval and fuzzy linear programming.Fuzzy Sets and Systems,vol.135,pp.151–177.

Jamison,K.D.;Lodwick,W.A.(2001):Fuzzy linear programming using a penalty method.Fuzzy Sets and Systems,vol.119,pp.97–110.

Jiang,C.;Han,X.;Liu,G.R.(2008):Uncertain optimization of composite laminated plates using a nonlinear interval number programming method.Computers&Structures,vol.86,pp.1696–1703.

Jiang,C.;Zhang,Q.F.;Han,X.;Liu,J.;Hu,D.A.(2015):Multidimensional parallelepiped model—a new type of non-probabilistic convex model for structural uncertainty analysis.International Journal for Numerical Methods in Engineering,vol.103,pp.31–59.

Kang,Z.;Luo,Y.(2010):Reliability-based structural optimization with probability and convex set hybrid models.Structural and Multidisciplinary Optimization,vol.42,pp.89–102.

Kang,Z.;Luo,Y.;Li,A.(2011):On non-probabilistic reliability-based design optimization of structures with uncertain-but-bounded parameters.Structural Safety,vol.33,pp.196–205.

Lin,S.C.;Kam,T.Y.(1992):Buckling analysis of imperfect frames using a stochastic finite element method.Computers&Structures,vol.42,pp.895–901.

Loeven,G.J.A.;Bijl,H.(2008):Probabilistic Collocation used in a Two-Step approach for efficient uncertainty quantification in computational fluid dynamics.CMES-Computer Modeling in Engineering and Sciences,vol.36,pp.193–212.

Long,X.Y.;Jiang,C.;Han,X.;Gao,W.(2015):Stochastic response analysis of the scaled boundary finite element method and application to probabilistic fracture mechanics.Computers&Structures,vol.153,pp.185–200.

Lodwick,W.A.(1990):Analysis of structure in fuzzy linear programs.Fuzzy Sets and Systems,vol.38,pp.15–26.

Ma,J.;Gao,W.;Wriggers,P.;Wu,T.;Sahraee,S.(2010):The analyses of dynamic response and reliability of fuzzy-random truss under stationary stochastic excitation.Computational Mechanics,vol.45,pp.443–455.

Maier,G.(1970):A matrix structural theory of piecewise linear elastoplasticity with interacting yield planes.Meccanica,vol.5,pp.54–66.

Melchers,R.E.(1999):Corrosion uncertainty modelling for steel structures.Journal of Constructional Steel Research,vol.52,pp.3–19.

Moens,D.;Vandepitte,D.(2005):A fuzzy finite element procedure for the calculation of uncertain frequency-response functions of damped structures:Part 1-Procedure.Journal of Sound and Vibration,vol.288,pp.431–462

Möller,B.;Beer,M.(2008):Engineering computation under uncertainty–Capabilities of non-traditional models.Computers&Structures,vol.86,pp.1024–1041.

Muhanna,R.;Mullen,R.;Zhang,H.(2005):Penalty-Based Solution for the Interval Finite-Element Methods.ASCE Journal of Engineering Mechanics,vol.131,pp.1102–1111.

OneSteel Publications(2000):Hot-Rolled Structurals&Welded Sections 5th Ed.Sydney:OneSteel Market Mills.

Przemieniecki,J.S.(1985):Theory of Matrix Structural Analysis.New York:Dover Publication Inc.

Quaranta,G.(2011):Finite element analysis with uncertain probabilities.Computer Methods in Applied Mechanics and Engineering,vol.200,pp.114–129.

Rao,S.S.;Sawyer,J.P.(1995):Fuzzy finite element approach for analysis of imprecisely defined systems.AIAA Journal,vol.33,pp.2364–2370.

Sadovskýa,Z.;Guedes Soaresb,C.;Teixeirab,A.P.(2007):Random field of initial deflections and strength of thin rectangular plates.Reliability Engineering and System Safety,vol.92,pp.1659–1670.

Schuëller,G.I.;Jensen,H.A.(2008):Computational methods in optimization considering uncertainties–An overview.Computer Methods in Applied Mechanics and Engineering,vol.198,pp.2–13.

Tangaramvong,S.;Tin-Loi,F.;Wu,D.;Gao,W.(2013):Mathematical programming approaches for obtaining sharp collapse load bounds in interval limit analysis.Computers&Structures,vol.125,pp.114–126.

Tangaramvong,S.;Wu,D.;Gao,W.(2015):Interval Limit Analysis of Rigid Perfectly Plastic Structures.ASCE Journal of Engineering Mechanics,vol.141,no.1,pp.06014016.

Tao,Y.R.;Han,X.;Duan,S.Y.;Jiang,C.(2014):Reliability analysis for multidisciplinary systems with the mixture of epistemic and aleatory uncertainties.International Journal for Numerical Methods in Engineering,vol.97,pp.68–78.

Vryzidis,I.;Stefanou,G.;Papadopoulos,V.(2013):Stochastic stability analysis of steel tubes with random initial imperfections.Finite Element in Analysis and Design,vol.77,pp.31–39.

Wang,C.;Gao,W.;Song,C.;Zhang,N.(2014):Stochastic interval analysis of natural frequency and mode shape of structures with uncertainties.Journal of Sound and Vibration,vol.333,pp.2483–2503.

Wu,J.;Luo,Z.;Zhang,Y.;Zhang,N.;Chen,L.(2013):Interval uncertain method for multibody mechanical systems using Chebyshev inclusion functions.International Journal for Numerical Methods in Engineering,vol.95,pp.608–630.

Wu,D.;Gao,W.;Li,G.;Tangaramvong,S.;Tin-Loi,F.(2015):Robust assessment of collapse resistance of structures under uncertain loads based on Info-Gap model.Computer Methods in Applied Mechanics and Engineering,vol.285,pp.208–227.

Xia,B.;Yu,D.;Han,X.;Jiang,C.(2015):Uni fied response probability distribution analysis of two hybrid uncertain acoustic fields.Computer Methods in Applied Mechanics and Engineering,vol.276,pp.20–34.

Yang,Z.C.;Li,K.F.,Cai,Q.(2013):Universal reliability method for structural models with both random and fuzzy variables.CMES:Computer Modeling in Engineering and Sciences,vol.95,pp.143–171.

Yang,Z.C.;Sun,W.C.(2013):A set-based method for structural eigenvalue analysis using Kriging model and PSO algorithm.CMES-Computer Modeling in Engineering and Sciences,vol.92,pp.193–212.

Zhenyu,L.;Qiu,C.(2001):A new approach to fuzzy finite element analysis.Computer Methods in Applied Mechanics and Engineering,vol.191,pp.5113–5118.

Appendix A:proof of equivalency of formulations between traditional and alternative finite element approaches for linear structural behaviour analysis

By substituting Eq.(9)into Eq.(10),the resultant is:

Furthermore,let K=CTSC,it is evident that Eq.(A2)coincides with the traditional FE formulation for 2D truss structural behaviour analysis with the consideration of thermal effects.

Appendix B:proof of equivalency of formulations between traditional and alternative finite element approaches for second order geometrically nonlinear analysis of 2-dimensional truss structure

By substituting Eq.(44)into Eq.(48),and Eq.(45)into Eq.(49),the resultants are:

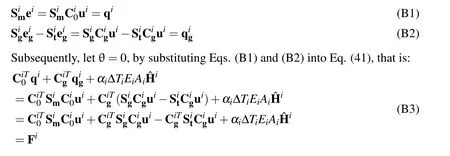
Appendix C:proof of equivalency of formulations between traditional and alternative finite element approaches for second order geometrically nonlinear analysis of 2-dimensional frame structure

From traditional FEM,the total strain of theith 2D frame element is a nonlinear function which can be expressed as[Przemieniecki(1985)]:

Lidenotes the length of theith 2D frame element;yis measured from the neutral axis of the beam anddenotes thedisplacement aty=0;and forj=1,...,6,denotes the displacement at thejth degree of freedom of theith element.

When thermal effect is considered,the elastic strainof theith element can be expressed as:

Thus the elemental potential energy is:

By neglecting the higher order termand implementing the Part I of Castigliano’s theorem[Przemieniecki(1985)],the governing equation for the second order geometrically nonlinear analysis of theith frame element can be formulated as:

with abbreviation:

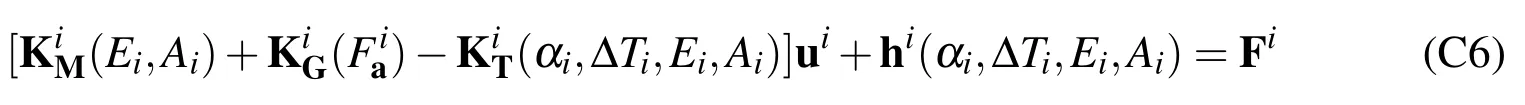
Eqs.(C5)and(C6)formulate the governing equations for the second-order geometrically nonlinear analysis of 2D frame elementithrough traditional FEM.It is illustrated here that the alternative FE model adopted in this study is equivalent to the traditional FEM approach.

By substituting Eq.(57)into Eq.(61),and Eq.(58)into Eq.(62),the resultant equations are:

Furthermore,let θ=0,and substitute Eqs.(C7)and(C8)into Eq.(54),the resultant is:

where

In addition,if the vector forms are implemented,the corresponding vector form of Eq.(C9)would be coincide with Eq.(C5).

1Centre for Infrastructure Engineering and Safety(CIES),School of Civil and Environmental Engineering,The University of New South Wales,Sydney,NSW 2052,Australia

2Corresponding author,Email:w.gao@unsw.edu.au

3School of Electrical,Mechanical and Mechatronic Systems,The University of Technology,Sydney,NSW 2007,Australia