Solving a Class of PDEs by a Local Reproducing Kernel Method with An Adaptive Residual Subsampling Technique

H.Rafieayan Zadeh,M.Mohammadi,2and E.Babolian

Solving a Class of PDEs by a Local Reproducing Kernel Method with An Adaptive Residual Subsampling Technique

H.Rafieayan Zadeh1,M.Mohammadi1,2and E.Babolian1

A local reproducing kernel method based on spatial trial space spanned by the Newton basis functions in the native Hilbert space of the reproducing kernel is proposed.It is a truly meshless approach which uses the local sub clusters of domain nodes for approximation of the arbitrary field.It leads to a system of ordinary differential equations(ODEs)for the time-dependent partial differential equations(PDEs).An adaptive algorithm,so-called adaptive residual subsampling,is used to adjust nodes in order to remove oscillations which are caused by a sharp gradient.The method is applied for solving the Allen-Cahn and Burgers’equations.The numerical results show that the proposed method is efficient,accurate and be able to remove oscillations caused by sharp gradient.

Local reproducing kernel method,method of lines,Newton basis functions,adaptive residual subsampling algorithm.

1 Introduction

During last decades,meshless methods are considered by many researchers.Unlike traditional numerical methods in solving PDEs,meshless methods[Belytschko,Krongauz,Organ,Fleming,and Krysl(1996)]need no mesh generation.Taking translates of kernels as trial functions in collocation methods,which are truly meshless,leads to a highly successful method[C.Franke(1998);Huang,Ren,and Russell(1990a);Huang,Ren,and Russell(1990b)].Implementation of these methods is easy and allow good accuracy at low computational cost.In addition,it was proven recently[Schaback(2015)]that symmetric collocation using kernels is optimal along all linear PDE solvers using the same input data.There are plenty of papers which use kernel-based methods for solving various problems[Abbas-bandy,Azarnavid,and Alhuthali(2014);Atluri and Shen(2003);Dong,Alotaibi,Mohiuddine,and Atluri(2014);Elgohary,Dong,Junkins,and Atluri(2014);Han and Atluri(2014);Hon and Schaback(2008);Mohammadi and Mokhtari(2014);Mohammadi and Mokhtari(2011);Mohammadi and Mokhtari(2013);Mohammadi,Mokhtari,and Panahipour(2013);Mohammadi,Mokhtari,and Panahipour(2014);Mohammadi,Mokhtari,and Schaback(2014);Mohammadi,Mokhtari,and Isfahani(2014);Mokhtari,Isfahani,and Mohammadi(2012)].

It is well known that representations of kernel-based approximants in terms of the standard basis of translated kernels are notoriously unstable.A more useful basis,so-called Newton basis,is offered in[Muller and Schaback(2009)].The Newton basis turns out to be orthonomal in the reproducing native Hilbert space,and it is complete,if in finitely many data locations are reasonably chosen.A time saving calculation of Newton basis arising from a pivoted Cholesky factorization has been introduced in[Pazouki and Schaback(2011)].

For the time-dependent PDEs,a spatial interpolation is applied by using expansion in terms of kernel functions.But since the coefficients are time-dependent,a system of ODEs is obtained.This is the well-known method of lines(MOL),and it turns out to be approximately useful in various cases.In this paper,we use expansion in terms of the Newton basis functions(NBFs)for constructing the spatial interpolation.

In global collocation methods,collocation matrix is made by considering the whole domain,since the obtained matrix will be full.This limits the applicability of those methods to solve large scale problems.But local methods[Chen,Ganesh,Golberg,and Cheng(2002);Lee,Liu,and Fan(2003);Mai-Duy and Tran-Cong(2002)]use overlapping sub-domains of the whole domain,thus a sparse matrix is obtained.A general idea behind the local reproducing kernel method is the use of the local sub clusters of domain nodes,named local influence domain,for approximation of the arbitrary field.With the selected influence domain,an approximation function is introduced as a sum of weighted NBFs.Then the collocation approach is used to determine weights.After the successful approximation function creation all the needed differential operators can be constructed by applying an arbitrary operator on the approximation function.The main advantage to using the local method is that less computer storage and flops are needed.

The kernel functions are defined by using a set of points called centers or trial points.The centers can set anywhere of given domain independently,therefore,center points can be moved or added or removed in the domain and this is the base of adaptive algorithms.Positions of the centers set influence on approximation quality and stability of the interpolation[Schaback(1995)],in addition,increasing number of centers causes large condition numeber of interpolation matrix.Adap-tive algorithms are often applied for problems containing rapid variations in the given domain.Different kinds of adaptive methods have been developed in the literature,e.g.Greedy algorithm[Ling,Opfe,and Schaback(2006);Ling and Schaback(2009)],upwind technique[Lin and Atluri(2000);Lin and Atluri(2001)],r-adaptive mesh method(moving mesh strategy)[Huang,Ren,and Russell(1994)].Four kinds of center choosing algorithms with some algorithmic analysis are introducedin[Gong,Wei,Wang,Feng,andWang(2010)].Inthispaper,weuseadaptive residual subsampling method[Driscoll and Heryudono(2007)],where nodes can be added or removed based on interpolation residuals evaluated at a finer point set.In the adaptive residual subsampling algorithm,an interpolant has been computed for the center set,the residual of the resulting approximation is sampled on a finer node set.Nodes from the finer set are added to or removed from the set of centers based on the size of the residual of the interpolation at those points.The interpolant is then recomputed using the new center set for a new approximation.

In this study,we use a local reproducing kernel method based on spatial trial space spanned by the NBFs accompanied with an adaptive residual subsampling technique for the numerical solution of a class of PDEs including the Allen-Cahn and Burgers’equations with different kinds of initial and boundary conditions.The Allen-Cahn equation describes the motion of anti-phase boundaries in crystalline solids.It has been widely used in material science applications.The Burgers’equation is the simplest nonlinear model equation for diffusive waves in fluid dynamics.The Burgers’equation arises in many physical problems including one-dimensional turbulence,sound waves in a viscous medium,shock waves in a viscous medium,waves in fluid filled viscous elastic tubes,and magneto-hydrodynamic waves in a medium with finite electrical conductivity.The Burgers’equation is similar to the one dimensional Navier-Stokes equation without the stress term.

The rest of the paper is organized as follows.In section 2,the kernel-based trial functions and the NBFs are reviewed.The proposed local reproducing kernel method is given in section 3.The method is illustrated in section 4 by solving the nonlinear Allen-Cahn equation with mixed boundary conditions.In section 5,the adaptive residual subsampling algorithm is illustrated.Numerical experiments are given in section 6.The last section is devoted to a brief conclusion.

2 Kernel-based trial functions

Let Ω be a nonempty set.A functionK:Ω×Ω → R is called a kernel on Ω.LetK:Ω×Ω → R be a symmetric positive de finite kernel on Ω.This means that for all finite sets{xi∈ Ω,i=1,...,n}the kernel matrixA=[K(xi,xj)]i,j=1,...,nis symmetric and positive de finite.These kernels arereproducingin “native”Hilbert space NK=of functions on Ω in the sense

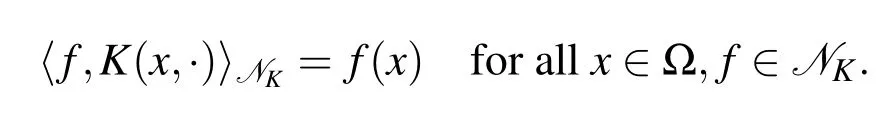
The most important examples are the Whittle-Matern kernelsreproducing in the Sobolev spacewhere Kνis the modiffed Bessel function of the second kind[Scahabck(2011)].The following will be independent of the kernel chosen,but ones should be aware that the kernel should be smooth enough to allow suffciently many derivatives for the PDE and additional smoothness for fast convergence[Wendland(2005)].For scattered nodesthetranslates Kj(x)=K(x,xj)are the trial functions.The Newton basis functions(NBFs)can be expressed by

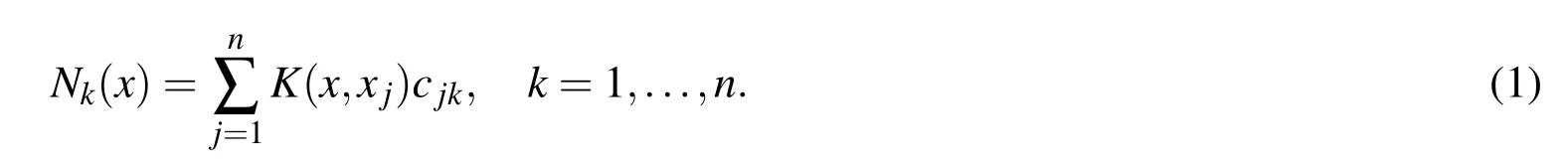
ConsideringN(x)=[N1(x)···Nn(x)],T(x)=[K(x,x1)···K(x,xn)]andC=[cjk]j,k=1,...,n,Eq.(1)can be written as

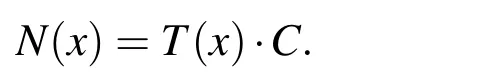
Subsequently,we haveN=A·C,where,N=[Nj(xi)]i,j=1,...,nandA=[K(xi,xj)]i,j=1,...,n.It has been proved[Pazouki and Schaback(2011)]that the Cholesky decompositionA=L·LTwith a nonsingular lower triangular matrixLleads to the Newton basis

with

Hence the condition number of the collocation matrix corresponding to the NBFs is smaller than the one corresponding to translated kernels.Consequently,using the NBFs for collocation will lead to more stable methods than using the basis of translates.Note that,

where,L can be any linear operator like derivatives.Moreover,for computing the values of the Newton basis at the other points,for example(2)is used.The Newton basis commonly is constructed by positive de finite kernels like radial basis functions(RBFs).The RBF is defined as

where{xj∈Ω,j=1,...,n}is a set of distinct points called centers.Some kinds of RBFs are given in Tab.1.The RBFs may have a free parameter,called the shape parameter,denoted by ε.As the shape parameter changes,the shape of the RBFs changes,and subsequently the accuracy of interpolant and the condition number of the interpolation matrix will change.For interpolation of scattered data by RBFs,an uncertainty relation between the error and the condition of the interpolation matrix is proven.It states that the error and the condition number cannot both be kept small[Schaback(1995)]and there is a trade-off between the accuracy and the condition number.Note that the GA,IMQ and MS RBFs are examples of positive de finite kernels and can be used for constructing the NBFs.

Table 1:Some kinds of RBFs

3 Local reproducing kernel method

Consider the following time-dependent PDE

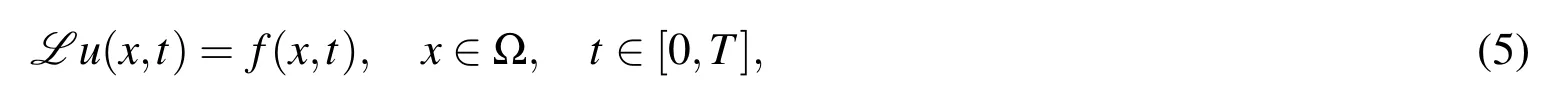
with boundary condition

and initial condition

where L:H→Fis a differential operator,HandFare Hilbert spaces of functions on,B is Dirichlet or Neumann or mixed boundary condition operator and I is a linear operator.It is assumed that the problem(5)–(7)is well-posed.We choose discrete pointsX=and a symmetric positive definite kernelK:Ω×Ω→R.LetXI={xi,i=1,...,ni}be the interior points andXB={xi,i=ni+1,...,n}be the boundary points,whereniis the number of interior points.For eachxi∈X,we consider a stencil Ωi=which contains the centerxiand itsm-1 nearest neighboring points.In addition,are considered as the NBFs corresponding to the stencilTo approximate the solutionu(x,t),we consider kernel-based approximant in terms of the NBFs on the local domain Ωiinstead of the whole domain Ω.Then the approximate solution in the local domain Ωiwill be in the following form

Therefore,forxi∈Ωiwe have

Consequently,(9)can be written as the following vector form

where,Ni=By using(8)the linear system

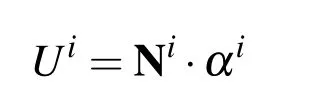
is obtained,where

and

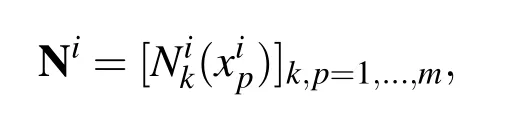
thus

By substituting(11)in(10)we have

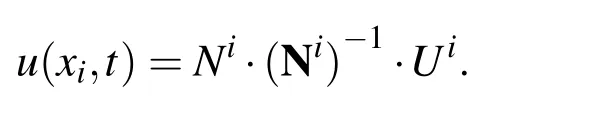
We now write the PDE(5)at a pointxi∈XIas follows

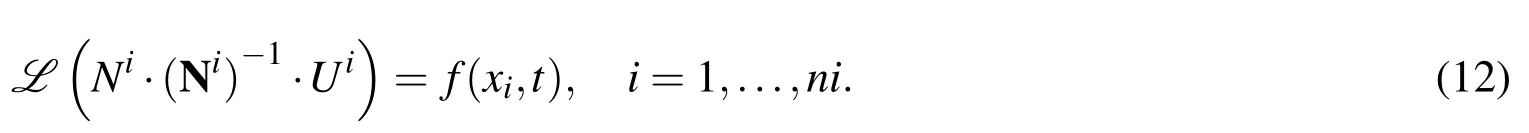
The boundary condition(6)implies that

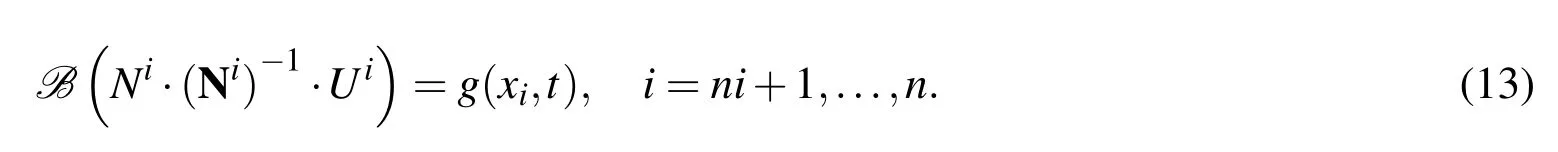
Moreover,(7)results

where IU(0)=[Iu(x1,0)···Iu(xn,0)]TandU0=[u0(x1)···u0(xn)]T.The equations(12)–(13)with the initial condition(14)lead to a system of ODEs at which the unknown vectorU=[u(x1,t)···u(xn,t)]Tis to be determined.In order to obtain a matrix form for the ODE system,matrices of spatial derivatives must be calculated.For the spatial partial derivatives,we have

Now for constructing global derivative matrices from local contributions,we de fine globalni-by-nsparse matricesD(s),according to derivatives appeared in(5),of the form

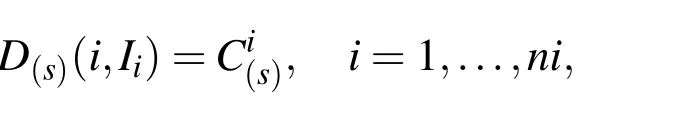
whereIiis a vector that contains the indices of centerxiand it’sm-1 nearest neighboring points.To clarify proposed method,it is applied for solving the Allen-Cahn equation in the next section.

4 Method validation

In this section,we apply the proposed method for solving the Allen-Cahn equation of the form

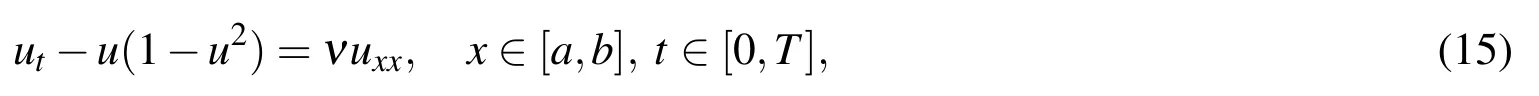
with mixed boundary conditions,

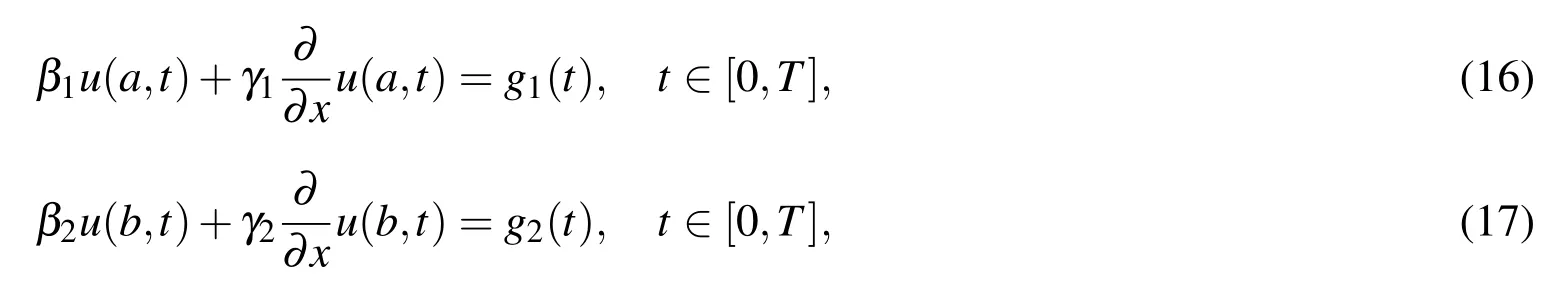
and initial condition,

where β1,β2,γ1,and γ2are known parameters,g1(t)andg2(t)are known functions,and ν is the kinematics viscosity.LetX={x1,x2,...,xn-1,xn}be discretization points in the interval[a,b]wherex1=a,andxn=b.Based on the methodology and notation described in the previous section,we write the PDE(15)at a pointxi,i=2,...,n-1,as follows

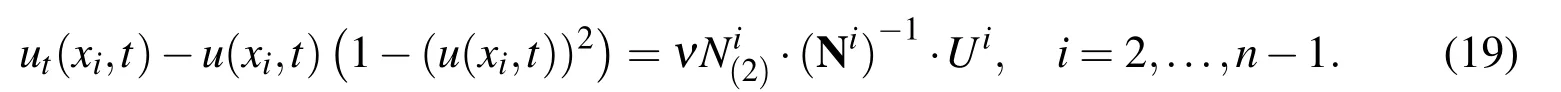
Then the equation(19)leads to the following matrix form

where.∗ and.∧ denote the pointwise product and power between two matrices or vectors,

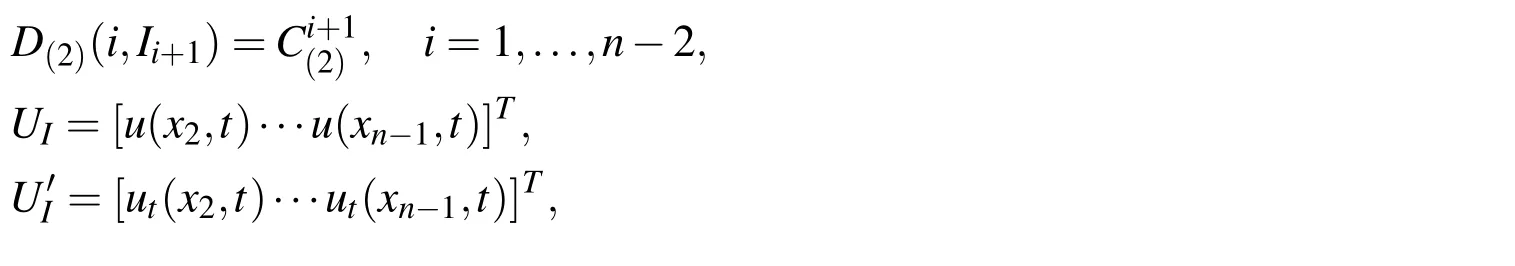
and 1 is a(n-2)-by-1 vector with 1 in its entries.Now we implement the boundary conditions(16)–(17)at the pointsx1andxnas follows

Let the 2-by-nsparse matrixWbe as follows:

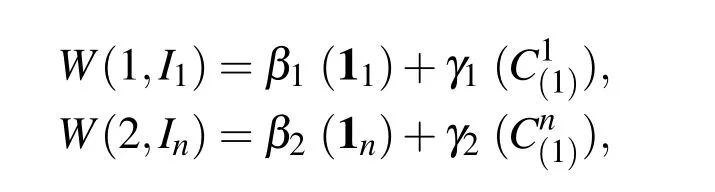
where 1iis a 1×nvector with 1 in theith entry and zero elsewhere.Then the Eqs.(21)–(22)lead to

So the unknown vector(u(xi,t),i=1,n)Tcan be written in terms of the unknown vectorUIby solving the following equations:

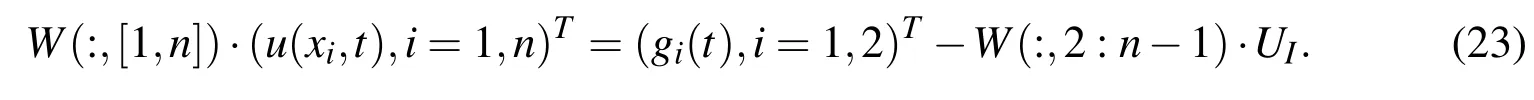
By subsituting(23)in(20),we get the system of ODEs with the initial conditions

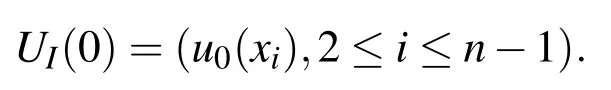
Note that the nonlinearity of the PDE is preserved,and a good ODE solver will automatically use a reasonable time-stepping and detect stiffness of the ODE system.

5 Adaptive residual subsampling algorithm

Since kernel-based methods are completely meshfree,some adaptive algorithms for finding optimal point sets may be devised.For example,in problems that exist rapid variations in given domain,such as steep gradients,corners,and topological changes resulting from nonlinearity,adaptive methods may be preferred over fixed grid methods.In order to achieve accuracy and stability,adaptive methods select optimal centers by moving,adding or removing points.In adaptive residual subsampling algorithm,some points may be added or removed by using computed residuals[Driscoll and Heryudono(2007)].In this section,we describe adaptive residual subsampling algorithm for a local reproducing kernel method based on spatial trial space spanned by the NBFs.

Implementation of adaptive residual subsampling technique for time-dependent PDEs is to alternate time stepping with adaptation.First,initial centers{xi,i=1,...,n}are generated usingnequally spaced points in the given domain.Then,using NBF interpolation at centers and initial condition of the PDE,unknown coefficients vector α =[α1···αn]Tis calculated from the linear system

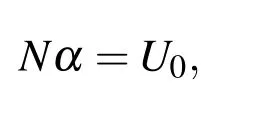
where,N=[Nj(xi)]i,j=1,...,nis the NBF matrix,U0=[u0(x1)···u0(xn)]Tandu0(x)is the initial condition function of the PDE.Now,the set1,...,n-1}is considered halfway between the centers.The residuals vectorris calculated by

where,Nyis the NBF matrix for the pointswhich is calculated by(2)–Points at which the residual exceeds a threshold θrare to become centers,and centers that lie between two points whose error is below a smaller threshold θcare removed.This means,ifri＞ θr,thenyiwill be added to centers set,and ifri＜ θcandri+1＜ θc,thenxi+1will be removed.This process is called coarse–re fine(coarse for removing centers and re fine for adding new points).Therefore,a new centers set is given and the coarse–re fine process is repeated while any new point can not be added.After ending coarse–re fine processes,a new centers set is obtained.These new centers are used to advance the discrete solution up to a predetermined timet=τ by using the local method,which is described in the previous section.τ must be large enough to avoid excessive adaptation steps,while keeping it small enough that the adaptation can keep up with emerging or changing features in the solution.So solution is obtained at the timet=τ.Now residual subsampling algorithm is applied by using the solution at this time level as a new initial state for further time.This process continues to achievet=T.

6 Numerical results

In this section,we present the results of our scheme for the numerical solution of some equations.Functions with steep variation in the domain are often employed.The obtained results state the ability of the method for adapting centers to the regions with steep variations.Some results without using adaptive method are presented to show unstability in regions with rapid variations.In this work,we take the MS and IMQ RBFs for constructing the Newton basis,in addition,we take τ=0.01.In examples,ν =1/Re,where Re is the Reynold number and ν is the kinematics viscosity.

Example 1:Consider the Allen-Cahn equation[Driscoll and Heryudono(2007)]

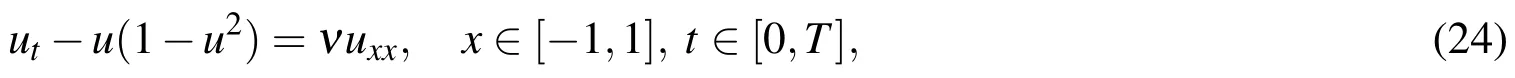
withRe=106,Dirichlet boundary condition,

and initial condition,

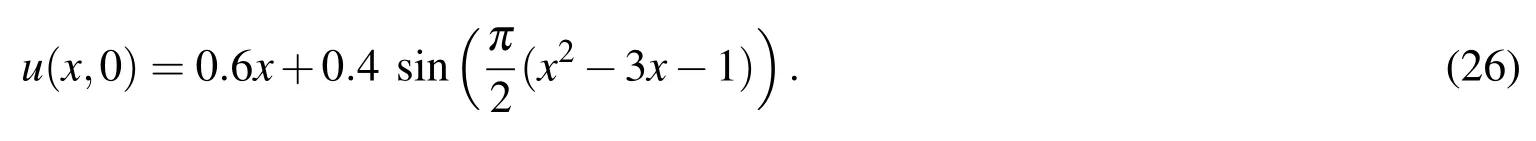
As shown in Fig.1,the solution of the equations(24)–(26),without using the adaptive residual subsampling method,have small oscillations in regions with steep gradients that are corrected by using the adaptive method.Adapting the nodes in steep gradients is shown in Fig.2.In this example,we use the MS RBF with the shape parameter ε=1,θr=10-3and θc=10-9.In addition,the number of nodes starts with 30 and finally grows to 176 atT=10.

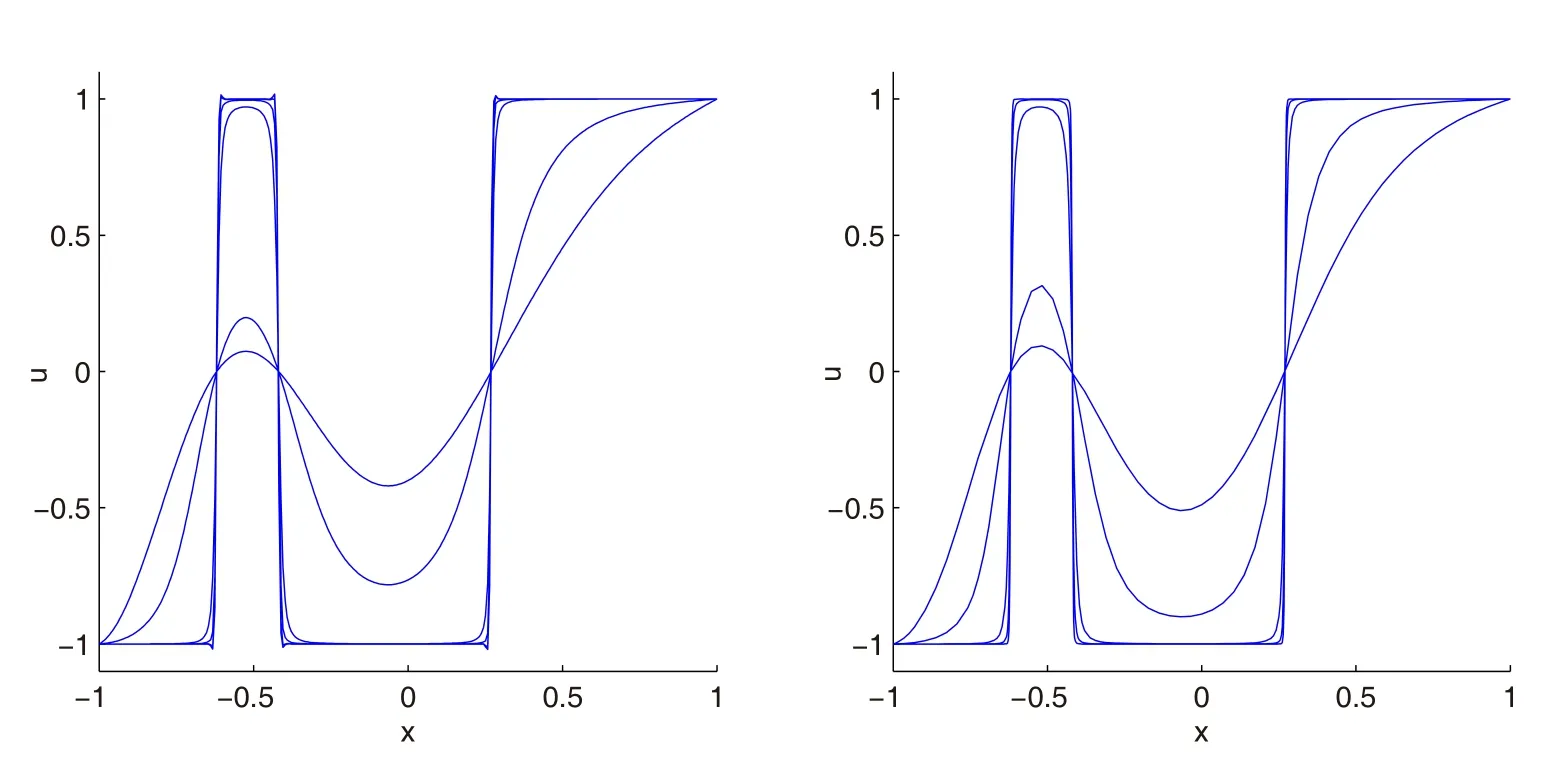
Figure 1:Solution of the Allen-Cahn equation,(left)without the adaptive method,(right)with the adaptive method.

Example 2:Consider the moving front problem given by the Burgers’equation[Driscoll and Heryudono(2007)]

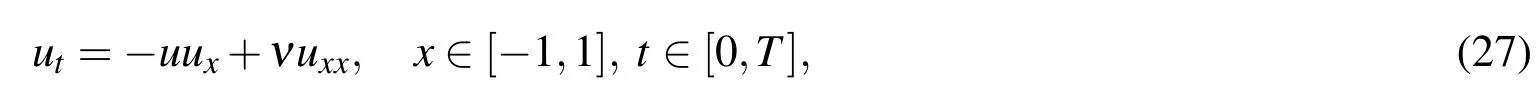
withRe=1000,Dirichlet boundary condition,

and initial condition,

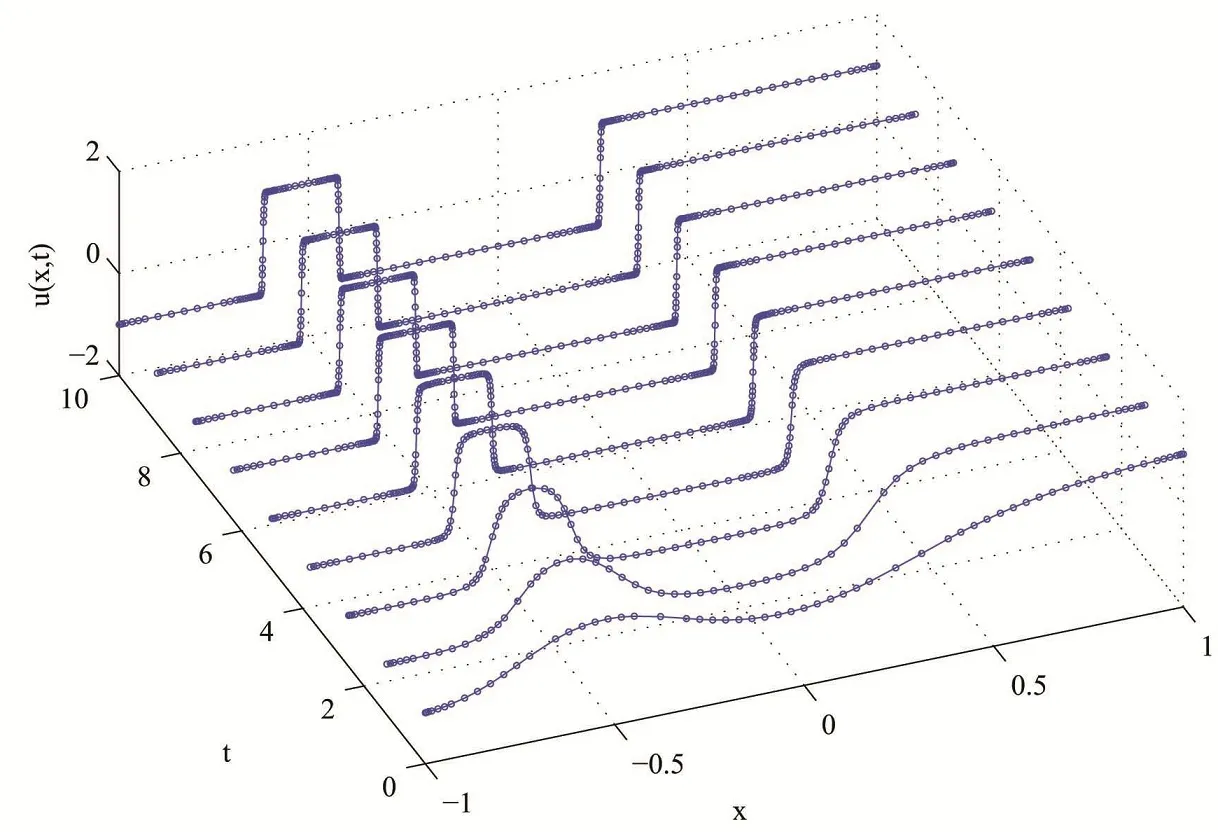
Figure 2:Solution of the Allen-Cahn equation with the adaptive method.Number of nodes increases in region with steep gradients.

As the previous example,the solution of the equations(27)–(29)generate steep front and consequently have unstabilities in steep front.Correction of these unstabilities and adaption of nodes by using the adaptive method are shown in Figures 3 and 4 respectively.Here,we employed the MS RBF with the shape parameter ε=1,θr=10-4and θc=10-8.Furthermore,number of nodes atT=1 grows to 76.

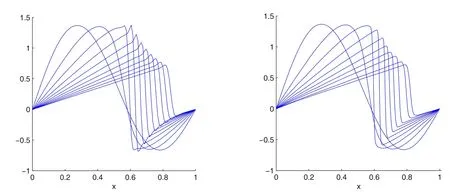
Figure 3:Solution of the equations(27)–(29),(left)whit out the adaptive method,(right)with the adaptive method.

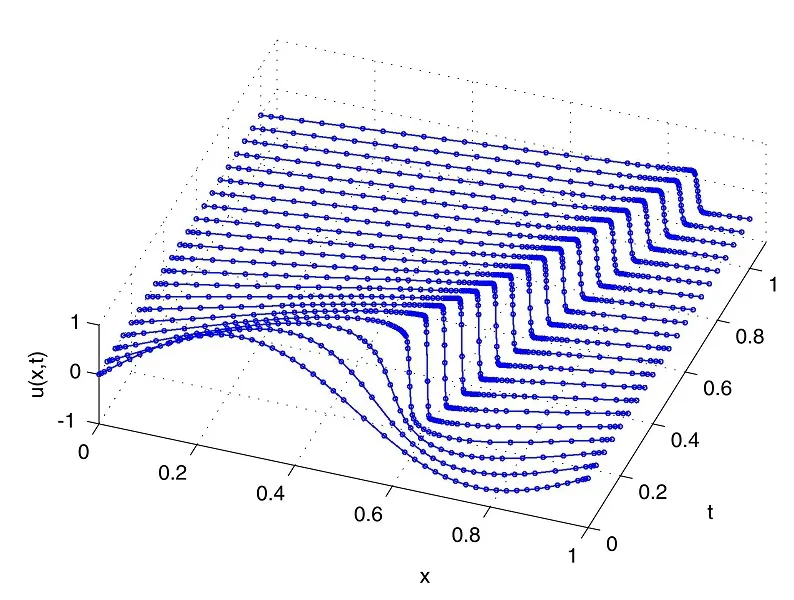
Figure 4:Solution of the equations(27)–(29);Adaption of nodes.

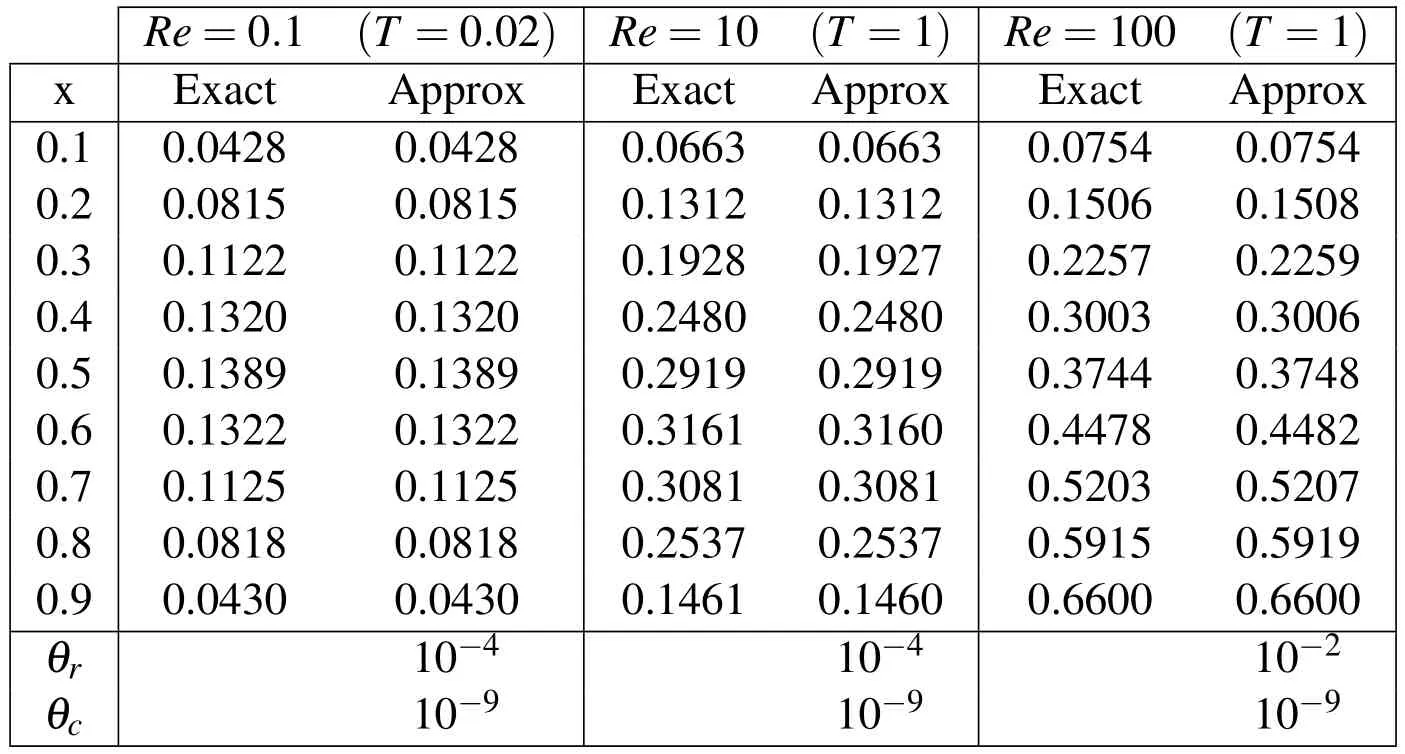
Table 2:Numerical results of the equations(30)–(32)for Re=0.1,10,100.

Example 3:Consider the Burgers’equation[Hon and Mao(1998)]

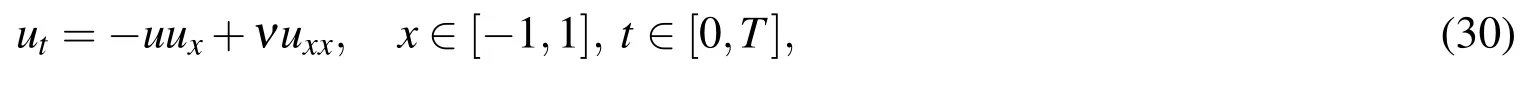
with Dirichlet boundary condition,

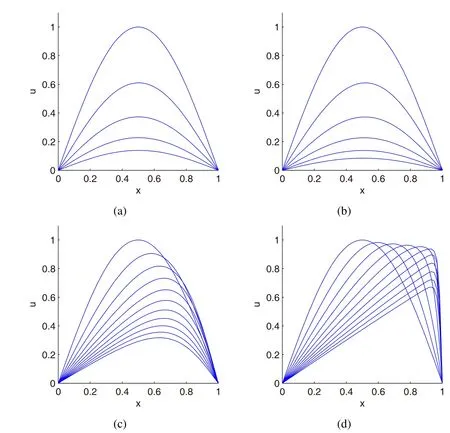
Figure 5:Solution of the equations(30)–(32),(a)Re=0.1 for T=0.02,(b)Re=1 for T=0.25,(c)Re=10 for T=1,(d)Re=100 for T=1.

and initial condition,

The exact solution of equations(30)–(32)is given by[Caldwell and Smith(1982)]

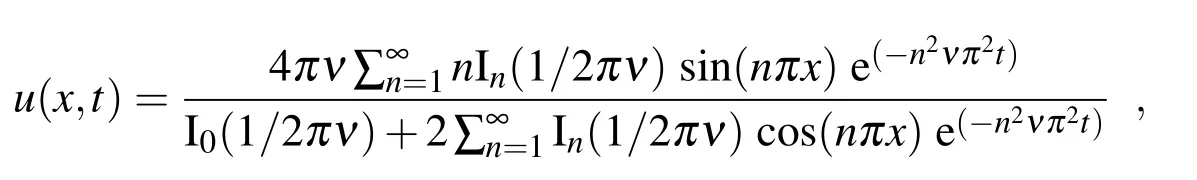
where Indenotes the modiffed Bessel function of ordern.In this example,we use the IMQ RBF with the shape parameters ε=5,5,5,5.8 forRe=0.1,1,10,100 respectively.The numerical solutions are shwon in Fig.5.Furthermore,forRe=0.1,10,100,comparison with the exact solutions and the thersholds are represented in Tab.2.

ForRe=1000,10000,the solution of equations(30)–(32)generates steep gradient towardx=1,subsequently the approximate solution has oscillations in regions with steep gradient.ForRe=1000,by implementing the proposed method with the MS RBF with the shape parameter ε=1.5,without using the adaptive algorithm,the oscillations are gradually disappeared when the number of nodes increases(Fig.6).The adaptive residual subsampling method starts with 30 nodes and gradually grows to maximum of 53 nodes,and consequently obtains solution atT=1 with 50 nodes(Fig.7).

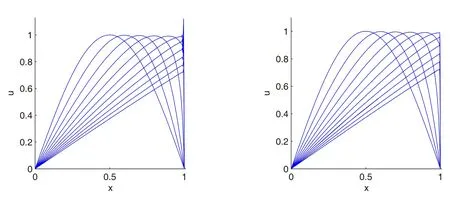
Figure 6:Solution of the equations(30)–(32),for Re=1000 whit MS RBF,(left)200 nodes,(right)1000 nodes.

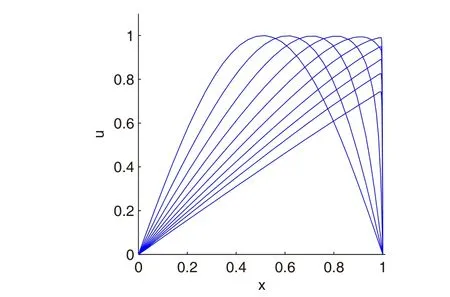
Figure 7:Solution of the equations(30)–(32)by using the adaptive method with 50 nodes at T=1.

ForRe=10000,the oscillations do not vanish even if the number of nodes be very large.Fig.8shows the oscillations with 1000 nodes and 2000 nodes in this case.As shown in Fig. 9, by using the adaptive residual subsampling algorithm and MS RBF with ε=1,the oscillations are disappeared atT=1 with 108 nodes(Fig.9).ForRe=10000,the numerical solution has been compared with the Christie accurate solution given in[Hon and Mao(1998)].Absolute error graph of implementation of the proposed method forRe=10000 is shown in Fig.9.In addition,adaption of nodes are shown in Fig.10.

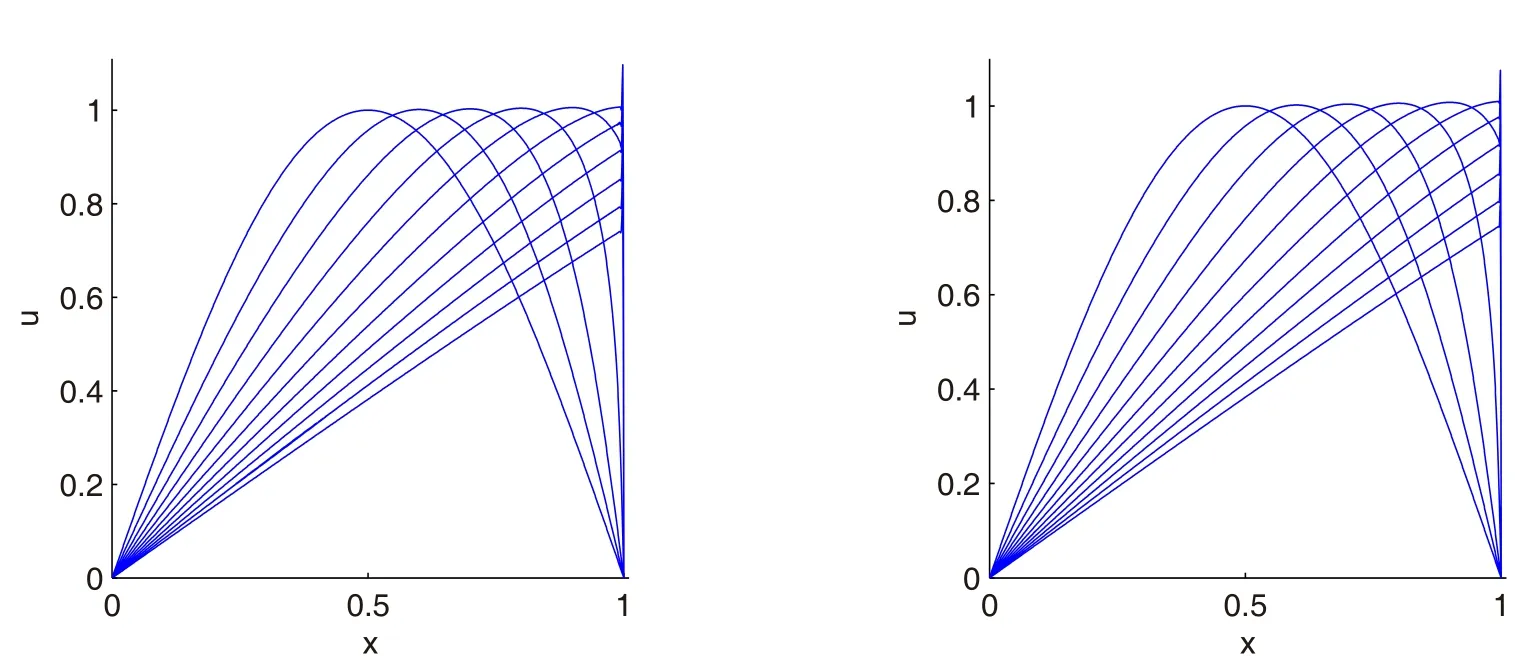
Figure 8:Solution of the equations(30)–(32),for Re=10000 with MS RBF,(left)1000 nodes,(right)2000 nodes.

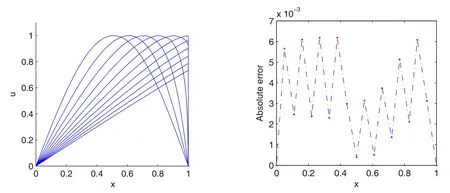
Figure 9:(left)Solution of the equations(30)–(32)for Re=10000 with the adaptive method,(right)Absolute error graph at x=0,0.05,0.11,0.16,0.22,0.27,0.33,0.38,0.44,0.50,0.55,0.61,0.66,0.72,0.77,0.83,0.88,0.94,1.

Example 4:Consider the Burgers’equation[Pugh(1995)]

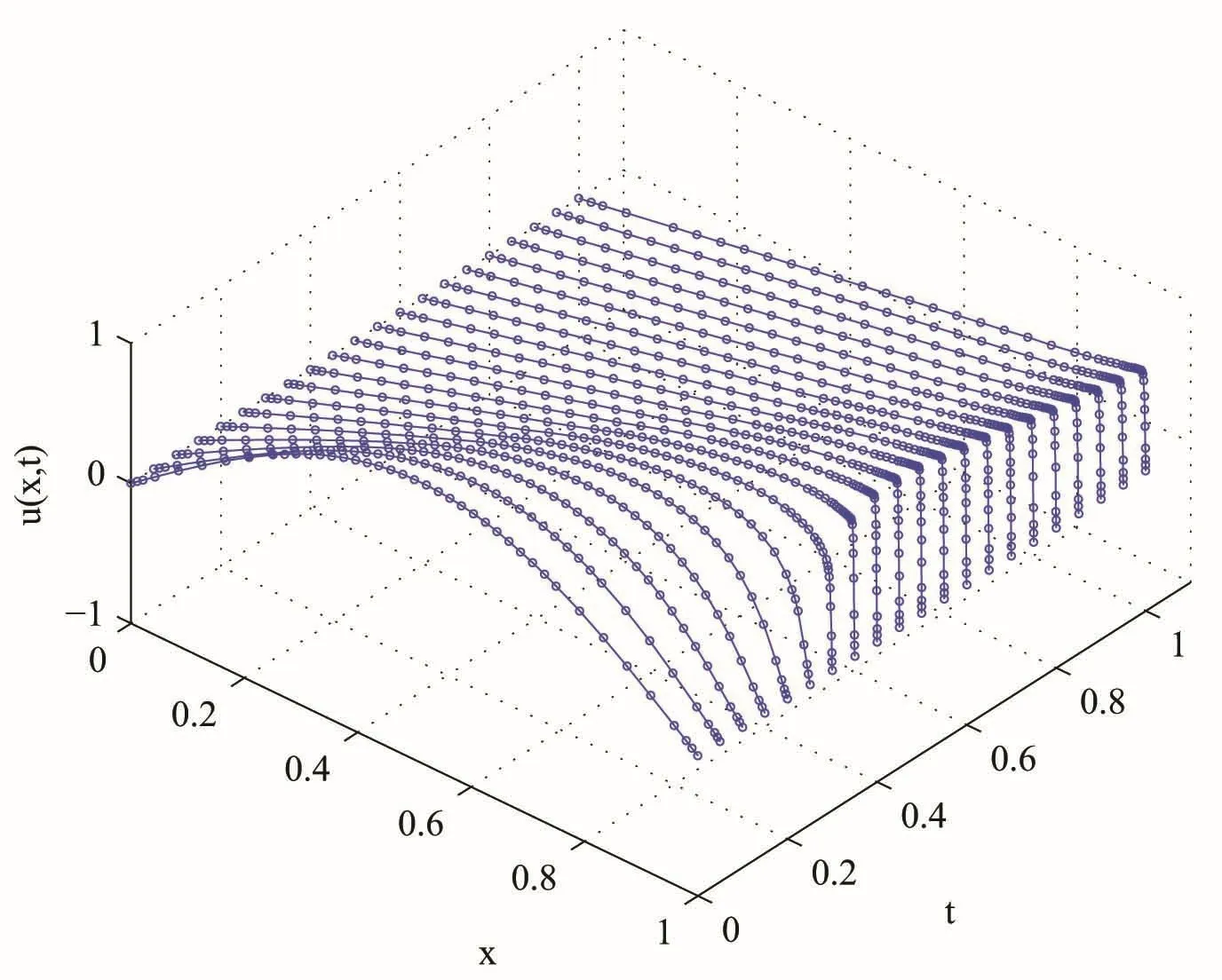
Figure 10:Solution of the equations(30)–(32);Adaption of nodes.

with Neumann boundary condition,

initial condition,

and

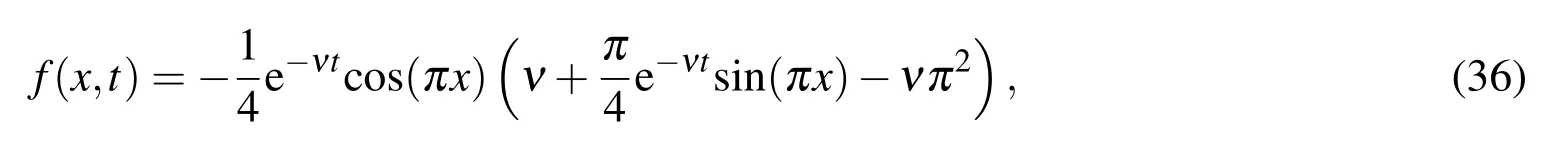
and the exact solution

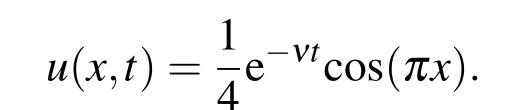
The equations(33)–(35)are solved forRe=60,120,240,1000,10000 by the proposed method with the MS RBF with the shape parameter ε=1.5.The absolute error graphs atT=0.5 are also shown in Fig.11.

7 Conclusion

Figure 11:Absolute error graphs for solution of the equations(33)–(35)at T=0.5.

In this paper,a local reproducing kernel method based on spatial trial spaces spanned by the Newton basis functions was used for solving some time-dependent PDEs.In addition,the adaptive residual subsampling algorithm was employed to correct oscillations.Numerical results show that the method works properly for problems with oscillatory behaviour due to steep gradients.It seems that this method can be applied for solving higher dimensional time dependent PDEs.We leave this to our further work.

Abbasbandy,S.;Azarnavid,B.;Alhuthali,M.(2014):A shooting reproducing kernel hilbert space method for multiple solutions of nonlinear boundary value problems.J.Comput.Appl.Math.http://dx.doi.org/10.1016/j.cam.2014.11.014.

Atluri,S.;Shen,S.(2003):The Meshless Local Petrov-Galerkin(MLPG)Method.Tech.Science Press.

Belytschko,T.;Krongauz,Y.;Organ,D.;Fleming,M.;Krysl,P.(1996):Meshless methods:an overview and recent developments.Comput.Methods Appl.Mech.,Engrg.,vol.139,pp.3–47.

C.Franke,R.S.(1998):Solving partial differential equations by collocation using radial basis functions.Appl.Math.Comput.,vol.93,pp.73–82.

Caldwell,J.;Smith,P.(1982):Solution of burgers’equation with a large reynolds number.Appl.Math.Modelling.,vol.6,pp.381–385.

Chen,C.;Ganesh,M.;Golberg,M.;Cheng,A.(2002):Multilevel compact radial basis functions based computational scheme for some elliptic problems.Comput.Math.Appl,vol.43,pp.359–378.

Dong,L.;Alotaibi,A.;Mohiuddine,S.;Atluri,S.N.(2014):Computational methods in engineering:A variety of primal&mixed methods,with global&local interpolations,for well-posed or ill-posed bcs.CMES Comput.Model.Eng.Sci.,vol.99,pp.1–85.

Driscoll,T.;Heryudono,A.(2007):Adaptive residual subsampling methods for radial basis function interpolation and collocation problems.Comput.Math.Appl,vol.53,pp.927–939.

Elgohary,T.;Dong,L.;Junkins,J.;Atluri,S.N.(2014):Time domain inverse problems in nonlinear systems using collocation&radial basis functions.CMES Comput.Model.Eng.Sci.,vol.100,pp.59–84.

Gong,D.;Wei,C.;Wang,L.;Feng,L.;Wang,L.(2010):adaptive methods for center choosing of radial basis function interpolation:a review.Lecture Notes in Comput.Sci.,vol.6377,pp.573–580.

Han,Z.;Atluri,S.(2014):On the(meshless local petrov-galerkin)mlpg-eshelby method in computational finite deformation solid mechanics-part ii.CMES Comput.Model.Eng.Sci.,vol.97,pp.199–237.

Hon,Y.;Mao,X.(1998):An efficient numerical scheme for burgers’equation.Appl.Math.Comput.,vol.95,pp.37–50.

Hon,Y.;Schaback,R.(2008):Solvability of partial differential equations by meshless kernel methods.Adv.Comput.Math.,vol.28,pp.283–299.

Huang,W.;Ren,Y.;Russell,R.D.(1990):Multiquadrics–a scattered data approximation scheme with applications to computational fluid dynamics i:surface approximations and partial derivative estimates.Computers Math.Appl.,vol.19,pp.127–145.

Huang,W.;Ren,Y.;Russell,R.D.(1990):Multiquadrics–a scattered data approximation scheme with applications to computational fluid-dynamicsii:solutions to parabolic,hyperbolic and elliptic partial differential equations.Computers Math.Appl.,vol.19,pp.147–161.

Huang,W.;Ren,Y.;Russell,R.D.(1994):Moving mesh partial differential equations(mmpdes)based on the equidistribution principle.SIAM J.Numer.Anal.,vol.31,pp.709–730.

Lee,C.;Liu,X.;Fan,S.(2003):Local multiquadric approximation for solving boundary value problems.Comput.Mech.,vol.30,pp.396–409.

Lin,H.;Atluri,S.(2000):Meshless local petrov-galerkin(mlpg)method for convection-diffusion problems.CMES Comput.Model.Eng.Sci.,vol.1,pp.45–60.

Lin,H.;Atluri,S.(2001):The meshless local petrov-galerkin(mlpg)method for solving incompressible navier-stokes equations.CMES Comput.Model.Eng.Sci.,vol.2,pp.117–142.

Ling,L.;Opfe,R.;Schaback,R.(2006):Results on meshless collocation techniques.Eng.Anal.Bound.Elem.,vol.30,pp.247–253.

Ling,L.;Schaback,R.(2009):An improved subspace selection algorithm for meshless collocation methods.Int.J.Numer.Meth.Engng.,vol.80,pp.1623–1639.

Mai-Duy,N.;Tran-Cong,T.(2002):Mesh-free radial basis function network methods with domain decomposition for approximation of functions and numerical solution of poisson equation.Eng.Anal.Bound.Elem.,vol.26,pp.133–156.

Mohammadi,M.;Mokhtari,R.(2011):Solving the generalized regularized long wave equation on the basis of a reproducing kernel space.J.Comput.Appl.Math.,vol.235,pp.4003–4014.

Mohammadi,M.;Mokhtari,R.(2013):A new algorithm for solving nonlinear schrödinger equation in the reproducing kernel space.Iranian J.Sci.Tech.,vol.37,pp.523–546.

Mohammadi,M.;Mokhtari,R.(2014):A reproducing kernel method for solving a class of nonlinear systems of pdes.Math.Model.Anal.,vol.19,pp.180–198.

Mohammadi,M.;Mokhtari,R.;Isfahani,F.T.(2014):Solving an inverse problem for a parabolic equation with a nonlocal boundary condition in the reproducing kernel space.Iranian J.Numer.Anal.Optimization.,vol.4,pp.57–76.

Mohammadi,M.;Mokhtari,R.;Panahipour,H.(2013):A galerkinreproducing kernel method:application to the 2d nonlinear coupled burgers’equations.Eng.Anal.Bound.Elem.,vol.37,pp.1642–1652.

Mohammadi,M.;Mokhtari,R.;Panahipour,H.(2014):Solving two parabolic inverse problems with a nonlocal boundary condition in the reproducing kernel space.Appl.Comput.Math.,vol.13,pp.91–106.

Mohammadi,M.;Mokhtari,R.;Schaback,R.(2014):A meshless method for solving the 2d brusselator reaction-diffusion system.CMES:Comput.Model.Eng.Sci.,vol.101,pp.113–138.

Mokhtari,R.;Isfahani,F.T.;Mohammadi,M.(2012):Reproducing kernel method for solving nonlinear differential-difference equations.Abstr.Appl.Anal.,vol.2012,pp.1–10.

Muller,S.;Schaback,R.(2009):A newton basis for kernel spaces.J.Approx.Theory.,vol.161,pp.645–655.

Pazouki,M.;Schaback,R.(2011):Bases for kernel-based spaces.J.Comput.Appl.Math.,vol.236,pp.575–588.

Pugh,S.(1995):Finite element approximations of burgers’equation.

Scahabck,R.(2011):Kernel-based meshless methods.Lecture Note,Gottingen.http://num.math.unigoettingen.de/schaback/teaching/AV2.pdf.

Schaback,R.(1995):Error estimates and condition numbers for radial basis function interpolation.Adv.Comput.Math.,vol.3,pp.251–264.

Schaback,R.(2015):A computational tool for comparing all linear pde solvers.Adv.Comput.Math.,vol.41,pp.333–355.

Wendland,H.(2005):Scattered Data Approximation.Cambridge University Press.

1Faculty of Mathematical Sciences and Computer,Kharazmi University,50 Taleghani Ave.,Tehran 1561836314,Iran

2Corresponding author