材料物理参数对摩擦副热变形影响的研究
2015-12-19崔建中王存堂谢方伟
崔建中,王存堂,谢方伟
(江苏大学 机械工程学院,江苏 镇江 212013)
材料物理参数对摩擦副热变形影响的研究
崔建中,王存堂,谢方伟
(江苏大学 机械工程学院,江苏 镇江212013)
摘要:为了深入研究材料物理参数对液粘调速离合器摩擦副的热变形影响,建立了摩擦副的热机耦合数学模型,采用有限元法对液粘调速离合器应用于软启动工况时摩擦副的热机耦合过程进行求解,详细分析了热传导系数、弹性模量和热膨胀系数对摩擦副应力场分布的影响。研究结果表明:摩擦副内、外径产生反向轴向位移,位移场中可见碟形翘曲变形;增大对偶片和摩擦衬片的热传导系数均有助于减小摩擦副的热应力;减小对偶片的弹性模量或热膨胀系数能有效减小摩擦副各表面的应力。
关键词:液粘调速离合器;热机耦合;应力场;热变形
液粘传动是流体传动领域中的一个新兴分支,它是基于牛顿内摩擦定律、利用液体的粘性或油膜的剪切力来传递动力,是继液压传动和液力传动之后的第3种以液体为工作介质的传动技术。液粘传动的基本原理如图1所示,两块平行放置的平板,间距为δ,两平板缝隙内充满着动力粘度为μ的牛顿流体,假设两板间的相对运动速度是V,则两板间的油膜将产生大小为F的剪切力,单位面积上能传递的剪切应力τ可表示为
(1)

图1 液粘传动原理图Fig.1 Schematic of HVD
液粘调速离合器是液粘传动技术的一个典型应用,其结构也与湿式离合器相似,主要应用在电力、石化、钢铁等大功率风机或水泵的调速,节能效果十分显著[1]。
当液粘调速离合器(HVD)应用于软启动工况时,即主动片在控制油压的作用下向被动片靠拢,摩擦副间隙内的油膜逐渐被挤压出来;同时,依靠摩擦力作用,将主动片的旋转运动传递给被动片,由于工作介质的特殊性,HVD可实现无级调速。在软启动过程中,摩擦副的相对滑动产生大量摩擦热,传入对偶片和摩擦片。由于摩擦副各部位的摩擦条件和运动状态有所不同,生成的摩擦热流也不同,导致摩擦片和对偶片的温升不均匀,从而引起表面材料的热变形。
摩擦副热变形的研究涉及到摩擦热的生成与热流分配理论,这是由于在滑摩过程中,摩擦因数、相对滑动速度以及接触压力等多种因素导致的动态变化过程十分复杂,因此相对滑动摩擦副产生的热问题是一个相当复杂的问题。林腾蛟等[2]采用有限元法对湿式离合器在空转和接合时摩擦片的热传导过程进行了数值模拟,计算得到了离合器空转时的效率以及润滑油出口温度;蔡丹等[3]采用试验方法研究了湿式离合器在不同位置的载荷作用下,摩擦片容易发生碟形翘曲变形和波浪形翘曲变形;邓涛等[4]对摩擦副在滑动摩擦阶段的热应力问题进行求解分析,比较不同厚度和不同环面宽度对对偶片表面温度的影响;孙冬野等[5]采用试验方法分析了热弹性失稳现象中对偶片的应力应变分布,研究表明,局部热点和接触压力有相互促进的作用;杨亚联等[6]采用热——机耦合仿真方法,分析了不同内外半径差、接合时间和接合次数对偶片的温度场和应力场分布;张金乐等[7]分析了摩擦副相对转速差、对偶片厚度和工作油压对对偶片温度场和应力场分布的影响,结果表明,高转速差加大了盘面的应力梯度,而对偶片厚度和工作油压均会对应力场分布的均匀性有不利影响。这些研究从多角度分析了摩擦副的热应力问题,但忽略了材料物理参数对摩擦副热变形的影响。
由于液粘调速离合器使用场合的特殊性以及软启动时间的长短,分析时需要考虑动态摩擦热流的作用效果以及材料的可靠性,因此,本文在三维瞬态热机耦合分析结果的基础上,考虑若干材料物理参数对摩擦副的热变形影响。
1摩擦副三维瞬态热机耦合有限元模型
1.1 瞬态热传导方程
由于摩擦副的轴对称结构,假设在软启动过程中,摩擦副各部分材料的热传导是各向同性的,并且旋转轴没有内热源,基于热传导理论,构建柱坐标系下摩擦副的瞬态热传导微分方程:
(2)
式中:下标i=s、f、c分别表示对偶片、摩擦衬片和芯片,Θi(r,zi,t)|i=s,f,c表示3种材料的温度,ρi、ki、ci(i=s、f、c)分别表示3种材料的密度、热传导率和比热容。
1.2 摩擦副热机耦合理论
根据热弹性理论,摩擦副受热传导后会发生膨胀,当受热不均匀时,热膨胀亦不均匀,从而产生线性应变[8]。材料处于弹性或塑性状态下应力应变关系为:

(3)
式中:[D]为弹性或弹塑性矩阵,{C}是与温度有关的向量。
在弹性区:
(4)
(5)
式中:{α}为热膨胀系数矩阵,T是温度。
在塑性区:
设材料的屈服函数为f(σx,σy……),其值在温度T、应变硬化指数K等条件下达到f0(σs,T,K)时,材料开始发生屈服。在加载过程中,加载曲面应满足一致性条件,即:
(6)
在塑性区内,全应变分量可以分解为:
(7)
根据流动法则,有:
(8)
联立式(6)~式(8),可得:
(9)
从而得到塑性区内的本构关系表达式:
(10)
式中:
(11)
(12)
令
(13)
(14)
则有

(15)
塑性区的加卸载由λ的值判定:λ>0是加载过程;λ=0是中性变载;λ<0是卸载过程。
节点上的接触压力[p]和单元应力{σ}的平衡关系是
(16)
其中,[B]是单元应变和节点位移之间的转换矩阵,V是摩擦副体积。
1.3 边界条件施加
为了得到控制方程的解,需要边界条件和初始条件。初始条件是摩擦副在初始时刻的温度分布,即
(17)
根据传热学中关于热边界条件的分类,可以建立3类不同的边界条件:
(1)摩擦副给定边界上的任意点N处,给定初始温度值,可表示为
(18)
(2)给定热流密度值。对任一微元面,假设在软启动过程中离合器摩擦能全部转化为热能,则热流密度q可表示为
(19)
式中:p(t)是摩擦片之间的接合油压,Pa;ω(t)是摩擦片和对偶片的相对滑动速度,m/s;dQ是热流量,W;dA是传热微元面,m2。
其中,主、被动摩擦片相对滑动速度ω(t)从液粘调速离合器的控制策略中获得;接合油压p(t)是在软启动过程中随着启动时间变化而变化,假设其软启动过程油压基本上随着启动时间呈线性变化,当完全接合后接合油压保持一定。
(3)给定对流换热。摩擦副的散热是通过润滑油膜与摩擦副表面的热交换实现的,其中摩擦接触区域是其主要的热交换区域,但对流换热效果并不明显,可以忽略不计,因此,如果摩擦副给定边界上的任意点N处,该点与外界的热量对流,则:
(20)
式中:h是对流换热系数,Θ是摩擦副的温度,Θ∞是润滑油的温度。
在摩擦副的实际软启动过程中,由流体或微凸体剪切产生的热量在摩擦副和油液中进行热传导或对流换热,整个热交换系统如图2所示。摩擦副内部均处于热传导状态,且设定摩擦副的初始温度值;摩擦副接触面AB和CD直接参与摩擦生热,用热流密度表示;摩擦副的内、外表面AE、BF、CG和DH与润滑油膜对流换热,采用对流换热条件。

图2 摩擦副热交换系统示意图Fig.2 Schematic of heat exchange system of friction pair
2摩擦副几何尺寸与材料物理参数
现以某液粘调速离合器实际结构为例进行摩擦副的热—结构耦合分析,摩擦副的几何尺寸如表1所示,若干组摩擦副材料的有关物理参数如表2所示。

表1 摩擦副几何尺寸
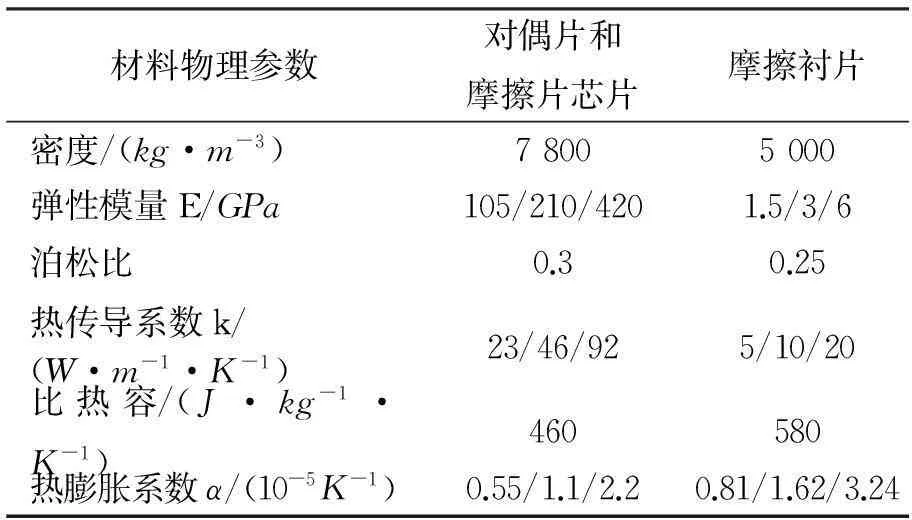
表2 摩擦副材料物理参数
3数值计算结果分析
3.1 变形分布
图3~图5分别表示不同时刻下摩擦副沿z轴的位移场分布,其中图3、图4(t=0.5s和t=2.5s)是从软启动过程中选取的时间点,图5(t=5s)则是启动过程结束后的时间点。

a正面
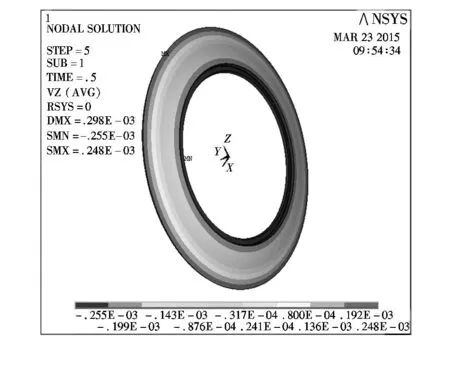
b 背面图3 摩擦副沿z轴位移场分布(t=0.5 s)Fig.3 Distribution of z-displacement field of friction pairs(t=0.5 s)

a正面

b 背面图4 摩擦副沿z轴位移场分布(t=2.5 s)Fig.4 Distribution of z-displacement field of friction pairs(t=2.5 s)
总体而言,摩擦副内外径呈现相反的位移变化趋势,即内径和外径分别沿z轴逆向和正向产生了轴向位移,其中,内径位移变化比外径要大,正向最大位移出现在摩擦副外缘,摩擦副产生了碟形翘曲变形。
3.2 热传导系数对摩擦副应力场分布的影响
为了详细研究摩擦副各处在软启动过程中的应力分布,本文从无油槽处的摩擦片与对偶片的内外两侧分别选取两个代表性节点,4个节点的位置分布如图6所示。

a正面

b 背面图5 摩擦副沿z轴位移场分布(t=5 s)Fig.5 Distribution of z-displacement field of friction pairs(t=5 s)

图6 摩擦副无油槽处4个节点位置分布Fig.6 Distribution of four nodes at the non-grooved regions of friction pairs
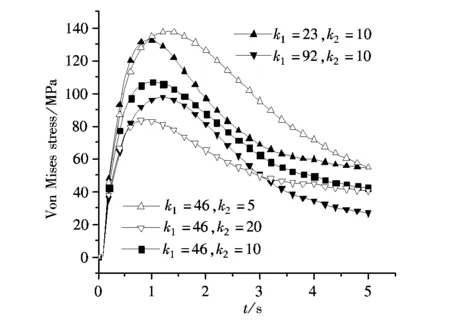
图7是摩擦副在不同节点、不同热传导系数时的VonMises应力变化曲线。由图7可知,增大对偶片和摩擦衬片的热传导系数均能有助于减小摩擦副的热应力(但两者的影响程序、影响范围有所区别)。综合来看,在启动过程中,摩擦衬片材料的热传导系数k2对摩擦副VonMises的应力影响较大;而在启动过程结束前后,对偶片材料的热传导系数k1的作用效果更为明显。
a 6 567

b 6 798

c 13 570

d 13 558图7 不同热传导系数时摩擦副的Von Mises应力变化曲线Fig.7 Von Mises stress history plot of friction pairs at different coefficients of thermal conductivity
对比发现,对偶片内表面与摩擦片外表面相似,而对偶片外表面与摩擦片内表面也相似。以对偶片外表面节点6 798为例,在启动开始到1.8s这段时间,k2对摩擦副应力的作用效果比k1明显;在1.8 s后,k1的作用才开始显现,说明摩擦副热应力变化的同一时刻,k1与k2分别起着不一样的作用。
3.3 弹性模量对摩擦副应力场分布的影响

3.4 热膨胀系数对摩擦副应力场分布的影响
热膨胀系数是由于温度改变而有胀缩的现象。图9是摩擦副在不同热膨胀系数时的VonMises应力变化曲线。从图9看出,与z向位移变化规律相似,增加对偶片的热膨胀系数能有效提高摩擦副各表面的VonMises应力,而摩擦衬片
的热膨胀系数对摩擦副的应力作用则十分有限。当增大对偶片的热膨胀系数,即α1/α1*=2时,对偶片内表面的最大应力达到210 MPa。

a 6 567

b 6 798

c 13 570

d 13 558图8 不同弹性模量时摩擦副的Von Mises应力变化曲线Fig.8 Von Mises stress history plot of friction pairs at different values of elasticity modulus

a 6 567

b 6 798

c 13 570
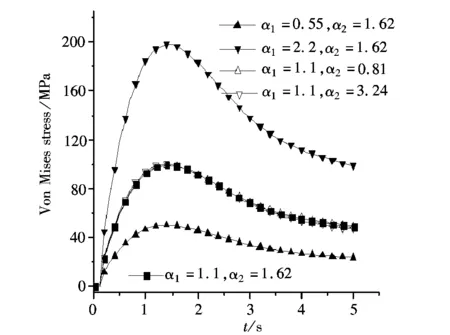
d 13 558图9 不同热膨胀系数时摩擦副的Von Mises应力变化曲线Fig.9 Von Mises stress history plot of friction pairs at different coefficients of thermal expansion
4结论
(1)摩擦副内径和外径分别沿z轴逆向和正向产生了轴向位移,正向最大位移出现在摩擦副外缘,摩擦副产生了碟形翘曲变形;
(2)增大对偶片和摩擦衬片的热传导系数均有助于减小摩擦副的热应力;
(3)减小对偶片的弹性模量能有效减小摩擦副各表面的应力;摩擦衬片材料的弹性模量对摩擦副的应力作用可忽略不计;
(4)减小对偶片的热膨胀系数能有效降低摩擦副各表面的应力,而摩擦衬片的热膨胀系数对摩擦副的应力作用可忽略不计。
参考文献:
[1]魏宸官,赵家象.液体粘性转动技术[M].北京:国防工业出版社,1996:1-3.
[2]林腾蛟,李润方,杨成云,等.湿式摩擦离合器瞬态热传导过程数值仿真[J].机械科学与技术,2003,22(1):34-41.
[3]蔡丹,魏宸官.湿式离合器片翘曲变形研究[J].北京理工大学学报,2000,20(4):449-451.
[4]邓涛,胡丰宾,孙冬野.湿式多片离合器的热弹性失稳分析[J].汽车工程,2012,34(10):918-922.
[5]孙冬野,胡丰宾,邓涛,等.湿式多片离合器翘曲特性模拟与试验[J].重庆大学学报,2010,33(5):1-6.
[6]杨亚联,张喀,秦大同.湿式多片离合器热机耦合温度场及应力场分析[J].中国机械工程,2014,25(20):2 740-
2 744.
[7]张金乐,马彪,张英锋,等.湿式换挡离合器温度场和应力场影响因素分析[J].北京理工大学学报,2010,30(6):660-664.
[8]李维特,黄保海,毕仲波,等.热应力理论分析及应用[M].北京:中国电力出版社,2004.
(责任编辑:张英健)
EffectofPhysicalPropertiesofMaterialonThermal
DeformationofFrictionPairs
CUIJianzhong,WANGCuntang,XIEFangwei
(SchoolofMechanicalEngineering,JiangsuUniversity,ZhenjiangJiangsu212013,China)
Abstract:The thermal-mechanical coupling model of friction pairs in hydro-viscous drive was established in order to deeply research the effect of physical properties of material on thermal deformation of friction pairs. A finite element technology was employed for analysis and calculation about the thermal-mechanical coupling process when it was used in the soft-start. A detail analysis of the effect of thermal conductivity, elasticity modulus and coefficient of thermal expansion on stress distribution was conducted. The results show that the inner side and outer side move in the opposite axial direction respectively and saucer-shaped warping deformation can be seen from the displacement field. Increase of thermal conductivities of separator disk and friction lining can help to decrease the thermal stress of friction pairs. Decrease of elasticity modulus or coefficient of thermal expansion can have a great effect on the decline of the stress of friction pairs.
Keywords:hydro-viscous drive; thermal-mechanical coupling; stress field; thermal deformation
作者简介:崔建中(1985-),男,江苏盐城人,博士生,主要研究方向为流体机械设计、液粘传动技术。
基金项目:江苏省普通高校研究生科研创新计划项目(CXLX13643);国家自然科学基金青年科学 (51205170);江苏省自然科学基金青年 (BK2012292);中国博士后科学基金第6批特别资助(2013T60502)
收稿日期:2015-03-27
中图分类号:TB131
文献标识码:A
文章编号:1671-5322(2015)02-0001-08
doi:10.16018/j.cnki.cn32-1650/n.201502001
