一种新的球形译码检测器性能分析

王艳丽

(渭南师范学院数学与信息科学学院，陕西 渭南 714000)

Performance Analysis of a New Sphere Decoding Detector

WANG Yanli

(College of Mathematics and Information Science， Weinan Normal University， Weinan 714000， China)



一种新的球形译码检测器性能分析

王艳丽

(渭南师范学院数学与信息科学学院，陕西 渭南 714000)

Performance Analysis of a New Sphere Decoding Detector

WANG Yanli

(College of Mathematics and Information Science， Weinan Normal University， Weinan 714000， China)

摘要：在多输入多输出(MIMO)系统中，基于深度优先球形译码检测器可以提供最优的性能，但其计算复杂度变换范围很大，而且仍然是天线数及调制阶数的指数函数。针对深度优先球形译码检测器复杂度较高和部分信号裁剪掉的可能性，设计出一种新的接收检测器，该检测器采用初始半径的选择和检测排序的思想降低复杂度，采用深度裁剪函数避免其部分信号被裁剪掉。

关键词：MIMO；深度优先译码检测器；深度裁剪函数；排序；初始半径

0　引言

多输入多输出(MIMO)技术利用多天线抑制信道衰落，其出发点是将多发送天线与多接收天线相结合，改善每个用户的通信质量或提高通信效率，无线信道容量随着天线数目的增加而线性增大[1]，在4G移动通信系统中作为一项关键技术得到长足发展[2]。但是在多天线系统中，每个接收端天线都能接收来自所有经过不同畸变的信道发送的数据，将这些数据分离是项艰巨而复杂的工作[3]。在众多的检测器中，最大似然检测器( ML)是最优的，但其非常高的计算复杂度限制了其应用。次优检测器如迫零(ZF)和最小均方误差(MMSE) 检测器以及干扰消除检测器拥有较低的复杂度，但检测效果不佳。

参考文献[4]提出了基于MIMO的球形译码检测，通过半径更新减少搜索空间，达到ML检测性能，且复杂度远远低于ML检测器。参考文献[5]基于传统Dijkstra球形译码，引入查表机制和单树更新软值方法，有效降低检测器复杂度。参考文献[6]指出，球形译码方法可以分为深度优先和宽度优先方法，其中，深度优先方法可以提供最优的性能，但其计算复杂度变换范围很大，仍然是天线数及调制阶数的指数函数。为此，在研究深度优先球形译码检测器的基础上对其进行了改进，主要改进思想体现在初始半径的选择、检测排序和深度裁剪函数的选择，通过仿真实验，验证了新的检测器能够避免深度优先检测器裁剪掉部分节点的缺点，并有效降低了复杂度。 dmin为最小欧式距离；p为概率；σ2为噪声方差。根据[9]的分析，为了降低复杂度，应使信噪比在增加的同时令p不断增加。

1　系统模型

在nR×nT的MIMO系统中，发送天线数为nT，接收天线数为nR，系统模型如图1所示。接收信号矢量Y表示为[7]：

(1)

X=[x1，x2，…,xnT]T为发送信号矢量，每个信号分量等概率地选自复星座集合S；Y=[y1，y2，…，ynR]T，各分量列数与每根发送天线传输的符号数有关；H为nR×nT复信道矩阵，用hi，j表示第i根发射天线到第j根接收天线的信道频域响应；V是均值为零，方差为σ2的高斯噪声，V=[v1，v2，…，vnR]。

图1　MIMO系统结构

2　新的深度优先球形译码检测器设计

2.1深度优先球形译码检测器

深度优先球形译码检测器不同于最大似然检测器，最大似然检测器将所有可能的解搜索一遍，这样必然导致该检测器复杂度较高，不适合实际应用。而深度优先球形译码检测器只是搜索部分解，部分解的圈定由预先设置好的半径决定，在欧式距离之外的点不予搜索，从根节点开始，每次只展开一个节点，直到叶子节点截止，然后循环完成所有解的搜索。

深度优先搜索具体思路如下：

a.确定初始半径，根据接收信号及信道矩阵来计算，选取欧式距离为0的根节点作为当前访问节点。

b.计算部分欧式距离，并根据欧式距离和裁剪半径来确定访问的节点。

c.根据欧式距离和裁剪半径循环实现节点的搜索。

2.2改进检测器

在深度优先球形译码检测器实现过程中，存在计算复杂度高、部分节点被剪裁掉的危险。针对其存在的缺点，改进思想体现在以下方面。

a.为了降低复杂度，初始半径c的确定选取传统SD检测器中的经验公式[8]：

(2)

(3)

Γ(·)为Gamma函数；n为接收信号维数；α为控制收缩速度的参数；ξ为搜索不到网格点的概率，取值为0.01。

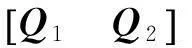
(4)

式(4)中上限用Ui表示，下限用Li表示。依据点到Ui和Li中间位置的距离，对调制星座点中的格点进行升序排序，若第i个坐标的可能值用zij表示，排序依据需要满足下式：

(5)

1≤j≤Ni，Ni表示在S中介于Li和Ui之间的点，Ni=length(Li，Ui，S)。

b.为了避免深度优先SD检测器求解过程中部分节点被剪裁掉的危险，采用基于深度优先的裁剪函数。

(6)

t为满足条件的节点数；k为层数。当k不断减少时，其函数值不断增大，即层数减少对应每层的节点数不断减少。

为了避免后续节点被删除，应用下式得到误帧率上界UB(pf)：

(7)

改进后的检测器系统如图2所示。

图2　改进后的检测器

3　复杂度和性能比较分析

3.1复杂度分析

深度优先球形译码检测器的计算复杂度比最大似然检测器小得多，但是，它的复杂度不确定，变化范围非常大，在极端情况下甚至接近于最大似然检测器，其应用受到了限制。在此，改进检测器采用初始半径的选择和引入排序思想的方法来降低复杂度。若用访问节点数来衡量复杂度，在高信噪比情况下，接近于比较小的数，具体而言，对于4QAM调制方式，在SNR为12时，改进检测器的访问节点数为123，低于原始检测器，如图3所示。

图3　检测器复杂度比较

3.2性能分析

实验采用Matlab进行仿真，构造2×2的MIMO系统，信道为已知的平坦瑞利衰落信道，均值为0且独立同分布的高斯白噪声，调制方式为4QAM。对比改进检测器和深度优先检测器的性能，仿真结果如图4所示。

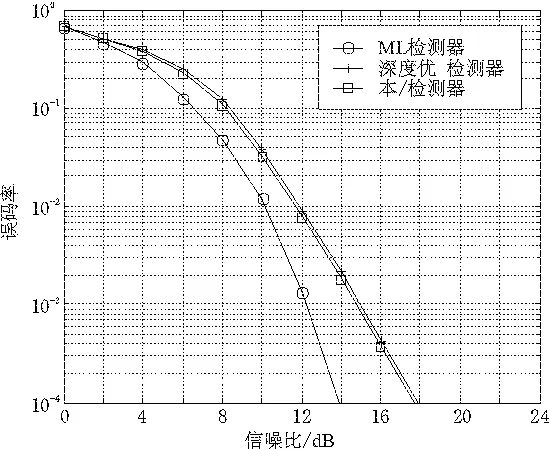
图4　3种检测器的误码率比较

由图4可以看出，ML检测器具有最优的检测性能，但其复杂度较高，不利于实际应用。与ML相比，本文改进检测器和深度优先球形译码检测器性能较差。而改进检测器和深度优先球形译码检测器性能相近，在高信噪比时，改进检测器性能较优，如在BER=10-2时，有0.2 dB的增益。

4　结束语

对深度优先球形译码检测器进行了分析，根据其存在的缺陷提出相应的改进，一方面，设计了一种新的排序方法，依据点到和中间位置的距离，对调制星座点中的格点进行升序排序，初始半径的选择采用原始半径的计算方法，有效降低复杂度；另一方面，为了避免深度优先球形译码检测器裁剪掉部分信号的缺点，采用深度裁剪函数，有效提高检测性能。通过Matlab仿真验证了改进检测器的有效性。

[1]Goldsmith A，Jafar S A，Jindal N， et al.Capacity limits of MIMO channels[J].IEEE Journal on Selected Areas in Communications， 2003，21(5):684-702.

[2]赵新雪，李琼，肖维杰，等.低复杂度最大似然MIMO信号检测算法[J].计算机工程与设计，2014， 35(1): 144-147.

[3]Artes H，Seethaler D，Hlawatsch F. Efficient detection algorithms for MIMO channels: a geometrical approach to approximate ML detection[J]．IEEE Transactions on Signal Processing，2003，51(11):2808-2820．

[4]Damen M，Gamal H，Caire G.On maximum likelihood detection and the search for the closest lattice point[J]. IEEE Transaction on Information Theory，2003，49(10):2389-2402.

[5]卢炳山，刘伟，俞晖，等.一种低复杂度多输入多输出球形译码算法[J].上海交通大学学报，2012，16(11): 1831-1837.

[6]毛新宇，程宇新，项海格.混合的深度优先及宽度优先球形译码算法[J].重庆邮电大学学报:自然科学版，2012，24(5):535-539.

[7]范忠亮，王永生，许家栋，等.一种用于高频谱利用率非确定性MIMO系统的高效球形译码算法[J].电路与系统学报，2012，17(3):48-53.

[8]李世平，王隆.结合最小均方误差的改进球形译码检测算法[J].计算机应用，2012，32(2):385-387.

[9]金鑫，倪芸，姚晓东.基于概率裁剪的球型译码算法[J].华东理工大学学报，2014，40(3):371-375.

Abstract：The best performance can be obtained by using a detector based on a depth-first sphere decoding detector in a MIMO system. However, the complexity changed often, and it is still an exponential function involving the modulation order and the number of antennas. In response to the complexity of depth-first sphere decoding, and the possibility of cutting off a part of the signal, a receiving detector is designed. The concept of choosing a detector using an initial radius and using detection sequencing reduces complexity but could possibly cut some signal; we adopted the depth clipping function to avoid cutting signal.

Key words：MIMO；depth-first sphere decoding detector；depth clipping function；ordering；initial radius

作者简介：王艳丽(1978-)，女，陕西咸阳人，硕士，讲师，研究方向为无线通信信号处理、无线网络技术。

基金项目：陕西省教育厅科研计划项目(2013JK1071)；渭南师范学院大学生创新创业训练计划(2014XK096)；校级特色学科建设资助项目(14TSXK02)；陕西省(数学)扶持学科建设资助项目

收稿日期：2015-03-04

文章编号：1001-2257(2015)06-0014-03

文献标识码：A

中图分类号：TP391.9；TN929.5