多尺度变换和粒子群优化的图像融合方法

那 彦，王赟鹏

(西安电子科技大学电子工程学院，陕西西安 710071)

图像融合技术在机器视觉和图像处理等领域有广泛的应用，它是将两个或多个传感器获取的图像加以综合处理而获得新图像［1］。随着不同变换的提出和发展，更多的变换被用于图像融合领域，例如:Wavelet变换、Contourlet变换、NSCT、Curvelet变换。但是，使用单一变换进行图像融合得到的结果往往不是最优的。为解决这一问题，本文提出了一种基于多尺度变换和粒子群优化的图像融合方法，对基于单一变换得到的融合结果在空域继续进行优化，并讨论了优化算法中初始图像质量对最终融合结果的影响。实验结果表明，文中提出的多尺度变换和粒子群优化的图像融合质量，优于基于四种不同变换的融合结果，且粒子群优化时选取偏差大的初始图像粒子，能够获得更好的融合结果。

1 多尺度变换的基本理论

Fourier分析反映了时间函数和频谱函数之间的关系，但尽管Fourier变换有很好的局部化频域的能力，却不具有局部化时间域的能力，后者对非平稳信号的研究和处理起到很大作用。因此从Fourier分析发展到了小波的理论和分析方法。小波变换是在有限宽度的范围内进行正交或者非正交的变换。小波的基函数是一种在频率和位置上不断变化的有限宽度的波形函数［2］。

Curvelet变换由脊波理论衍生而来，是由一种特殊的滤波过程和多尺度脊波变换组合而成的。Curvelet变换的核心是Curvelet基支撑区间表现为“长条形”其实际是“方向”性的一种体现，因此也称这种基具有“各向异性”，从而用更少的Curvelet变换系数来逼近奇异曲线，或者Curvelet变换能够更稀疏地表示图像的边缘［3－4］。

Contourlet变换是二维图像的一种新的无损表示方法。它是一种非自适应的方向多尺度分析方法［5］。二维可分离的小波基只有有限个方向，所以在细节和轮廓信息的表征上存在缺陷，而Contourlet变换的出现弥补了这一缺陷，它能实现在任意方向上的任意尺度分解。非下采样 Contourlet变换(NSCT)不仅具备Contourlet变换的多尺度特性和灵活的多方向展开特性，而且消除了Contourlet变换时的Gibbs效应，是适用于图像融合的良好多尺度分析工具［6－7］。

2 粒子群优化算法

粒子群优化算法(Particle Swarm Optimization，PSO)是一种基于进化理论的计算技术，该算法起源于对鸟群捕食的行为研究，是一种基于迭代的优化工具［8］。

基本的PSO算法中，首先系统随机初始化一组随机解，然后系统不断经过迭代计算，根据各粒子的适应度函数来优化目标从而求取最优解。适应度函数通过目标函数的设立和计算得到。每次迭代过程中，粒子通过计算适应度值，并跟踪粒子自身目前的最优解和整个种群找到的最优解这两个值来更新自身的速度和位置。假设在第k次迭代时，第i个粒子的速度为位置为，此时该粒子和整个种群找到的最优解分别为和Gbk。粒子速度和位置的更新按照下述公式进行。

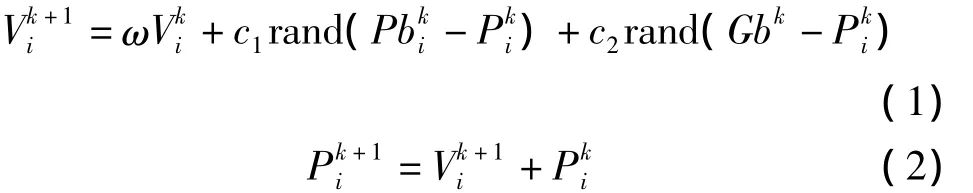
其中，c1、c2为学习因子;rand为(0，1)间的随机数;ω为惯性权重［9］。

本文算法对基本的PSO算法进行了改进。考虑到多聚焦图像的特征，选取信息熵参数和平均梯度参数为优化的两个目标，优化最终得到的是一组非支配解即Pareto最优解，从这组解中选择最终结果［10］。

设需优化的两个目标函数分别为F1和F2，对种群中的粒子根据POS算法分别计算由这两个目标函数得到的适应度值。假设在第k次迭代时，粒子i和整个种群对于这两个目标函数找到的最佳适应度值分别为P)的距离将和Gbk代入基本PSO算法中的粒子速度和位置更新公式，求得粒子新的位置和速度。

3 图像融合算法

基于4种不同的多尺度变换对源图像进行融合处理，分别得到融合图像。实验中，选取初始粒子分粒子之间偏差最小、粒子之间偏差最大、随机选取、取6个质量最差、取6个质量最好共5种情况。粒子间的偏差通过欧式距离计算。每种情况从图像集合M中选取6幅图像，重复5次，记录对应情况得到的结果评价参数的平均值。

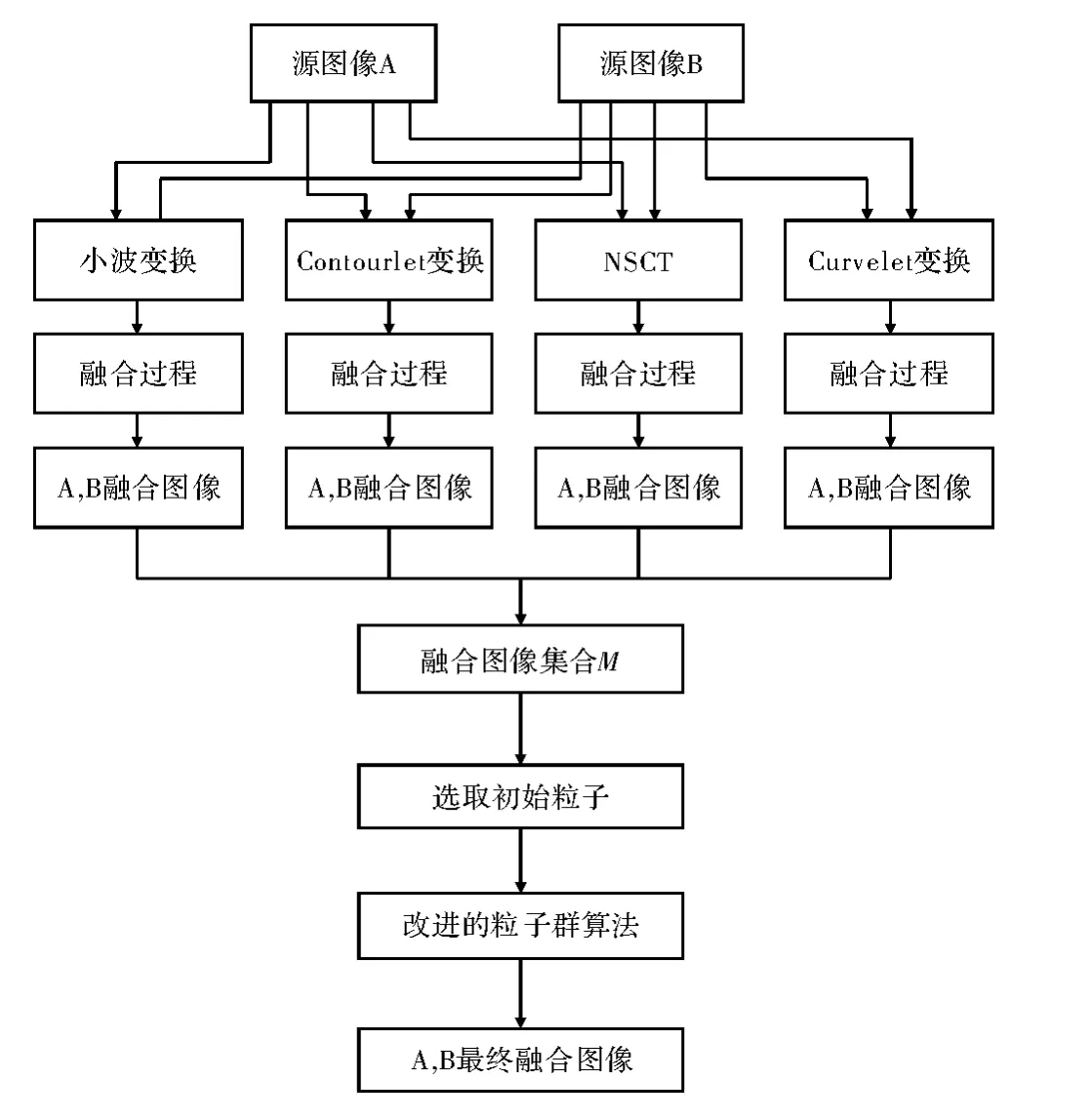
图1 多尺度变换和粒子群优化的图像融合算法流程图

4 仿真实验及结果分析

本算法主要针对多聚焦图像，利用Matlab验证算法的正确性。实验选取多聚焦的图像进行实验，两幅图像在实验前已经经过配准。

图2 多聚焦源图像

图3 基于不同变换的融合图像构成的图像集合M

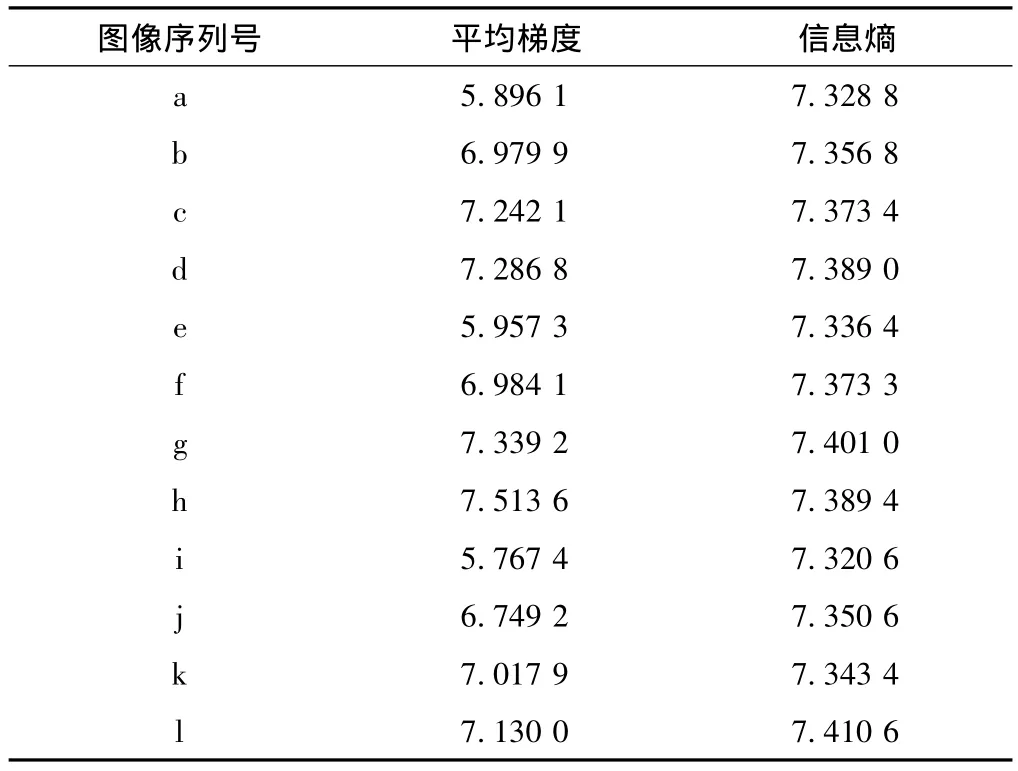
表1 图像集合M中图像评价参数表

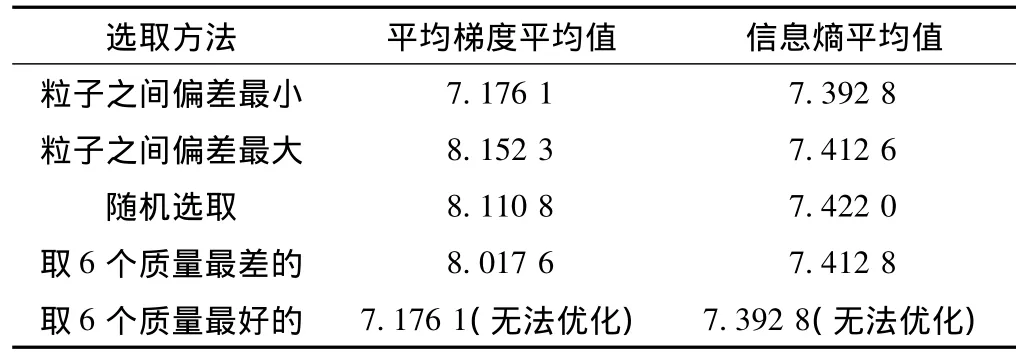
表2 粒子不同偏差情况下的融合结果的评价参数表

初始粒子图像集合M如图3所示，集合M中的图像评价参数如表1所示。实验进行时分粒子之间偏差最小、粒子之间偏差最大、随机选取、取6个质量最差、取6个质量最好这5种情况。每种情况从集合M中选取6个图像粒子，重复5次，记录对应情况得到的结果评价参数的平均值，结果如表2所示。表2中，平均梯度平均值记录5次实验得到的结果平均梯度的平均值，信息熵平均值记录5次实验得到的结果信息熵的平均值。其中，偏差最小、粒子之间偏差最大、随机选取、取6个质量最差这4种情况下均能正常优化;取6个质量最好的这种情况下无法优化，优化结果与初始输入一致，无优化效果。

分析以上结果，文中提出的多尺度变换和粒子群优化的图像融合质量，优于基于4种不同变换的融合结果。单纯取质量最好的粒子并不能一定提高融合结果的质量，而取最差的也未必不能得到好的结果。在粒子间偏差较少时，粒子在整个解空间中分布比较集中，搜索最优解时不容易找到较好的解，即容易陷入局部最优;而粒子间差异变化变大时，粒子在解空间中的分布变得分散，相对容易找到更好的解。因此，在做类似的实验时应尽量选取相互偏差大的图像作为优化的初始粒子。

5 结束语

提出了一种基于多尺度变换和粒子群优化的图像融合方法，并深入讨论了优化算法中初始图像质量对最终融合结果的影响。为证该算法的有效性，对图像融合中最常见的多聚焦图像融合进行了Matlab仿真。实验结果表明，提出的多尺度变换和粒子群优化的图像融合质量优于基于4种不同变换的融合结果，且粒子群优化时选取偏差大的初始图像粒子，能够获得更好的融合结果。因此，在做类似的实验时应尽量选取相互偏差大的图像作为优化的初始粒子。

［1］ 那彦，焦李成．基于多分辨分析理论的图像融合方法［M］．西安:西安电子科技大学出版社，2007．

［2］ 张彬．基于小波变换的图像融合方法研究［D］．青岛:山东科技大学，2012．

［3］ 蒋年德，王耀南，毛建旭．基于Curvelet变换的遥感图像融合研究［J］．仪器仪表学报，2008，29(1):61 －66．

［4］ 吴芳平，狄红卫．一种基于Curvelet变换的图像融合新算法［J］．光电子·激光，2008，19(7):963 －966．

［5］ 焦李成，侯彪，王爽．图像多尺度几何分析理论与应用［M］．西安:西安电子科技大学出版社，2008．

［6］ 童涛，杨桄，谭海峰，等．基于NSCT变换的多传感器图像融合算法［J］．地理与地理信息科学，2013，29(2):22－25．

［7］ 谭江波．基于NCST变换的多远图像融合算法研究［D］．杭州:浙江理工大学，2013．

［8］ 章小龙．基于粒子群优化算法的像素级图像融合［J］．漳州师范学报:自然科学版，2009(2):37－40．

［9］ 刘建华．粒子群算法的基本理论及其改进研究［D］．长沙:中南大学，2009．

［10］王宪，张方生，幕鑫，等．基于多目标粒子群算法的多传感器图像融合［J］．光电工程，2012，39(6):102 －110．