基于跳数修正的DV－Hop改进算法

韩 震，肖铁军

(江苏大学计算机科学与通信工程学院，江苏镇江 212013)

无线传感器网络［1］由大量廉价微型传感器节点组成，通过无线通信方式形成一个多跳的自组织网络系统，用于感知、采集和处理网络中感知对象的信息，现已广泛应用于环境、医疗、军事等领域。

定位技术作为无线传感器网络的核心技术之一，可分为基于测距(Range－Based)和与距离无关(Range－Free)的定位算法［2］。基于测距的定位算法需要获取节点间距离或角度信息，定位精度较高，但对节点硬件要求也较高;与距离无关的定位算法依赖网络连通度来计算未知节点与信标节点间距离实现定位，定位精度不如基于测距的定位算法，但其无需额外硬件，适用于对定位精度要求不高且成本敏感的场合。与距离无关的定位算法应用广泛，DV－Hop(Distance Vector－Hop)算法就是其中的一种典型算法。

针对DV－Hop算法定位精度不高的问题，相关研究已取得了一些成果。文献［3］采用最小二乘法修正信标节点间的平均跳距，算法的计算量较大;文献［4］将平均每跳距离取平均作为未知节点平均每跳距离，但不能解决节点间分布不均带来的估算误差;文献［5～6］使用RSSI(Received Signal Strength Indicator)加权修正跳数，但对于RSSI值依赖较大，产生误差;文献［7］采用跨境返回测距机制，通过判断两节点的位置关系将节点归类以减少定位误差，定位精度提升不明显;文献［8］对跳距细化并使用RSSI比值对跳数加权修正，但使用RSSI测距模型需要较大的计算量;文献［9］引入RSSI比值修正跳数，定位精度需进一步提高;以上算法对定位精度有一定提高，但有的计算量较大，有的未能考虑节点分布的可能情况。本文针对跳数进行水平及垂直修正，使跳数信息尽可能地反应节点真实距离关系，同时分析两节点之间的距离导致下一节点分布的可能性情况，采用修正角度优化节点间跳数，提高定位精度的同时降低计算量，最后仿真验证改进算法性能。

1 DV－Hop算法

DV－Hop算法［10］分为以下3个阶段:

(1)计算信标节点到其他节点的最小跳数:每个信标节点向邻居节点广播自身位置信息的分组。接收节点记录到每个信标节点的最小跳数，忽略来自同一信标节点的较大跳数分组，此时跳数加1，并转发分组信息。通过这个方法，网络中的节点获取到每个信标节点的最小跳数。

(2)计算未知节点到信标节点的实际跳段距离:信标节点根据式(1)计算平均每跳距离

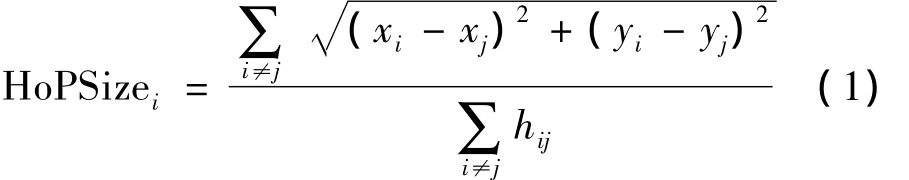
式(1)中，(xi，yi)，(xj，yj)分别是信标节点 i，j的真实坐标;hij是信标节点i，j的最小跳数;HopSizei是信标节点i的平均每跳距离。

未知节点i收到最近的平均每跳距离校正值后，计算到信标节点j的跳段距离dij如下

(3)利用三边测量法或极大似然估计法计算位置:未知节点获取3个跳段距离，使用三边测量法，3个以上跳段距离使用极大似然估计法得出自身位置信息。

2 DV－Hop算法改进

传统DV－Hop算法第一阶段获取节点间的最小跳数，然后依靠最小跳数计算出信标节点平均每条距离，最后未知节点使用最小跳数计算到信标节点的跳段距离。可见，跳数信息在DV－Hop算法中占据重要的位置，跳数信息的准确性直接影响到未知节点定位精度，但传统算法中，节点通信范围内的所有节点间跳数都是1跳，不能较好地反应出相邻节点实际距离关系，由此获取的最小跳数信息对实际平均每跳距离产生误差，最终影响未知节点的定位精度值。如图1所示。

图1 节点分布示意图

图1中，节点1、2、3水平分布，跳数 h12和 h13分别是1跳和2跳，但由于水平分布节点密度不均匀，实际距离d13并不一定是d12的2倍关系;节点3、4、5可以是水平与垂直分布的结果，跳数h35是跳数h34与h45之和，实际距离d35并非d34与d45之和，两者存在一定的误差。

针对图1所示情况，本文引入RSSI量化跳数，进行水平修正，在水平修正的情况下，引入修正角度，进行垂直修正。

2.1 水平修正

2.1.1 RSSI测距模型

无线传感器网络中应用最广泛的信号传播损耗模型是 Shadowing 模型［11］，表达式如下

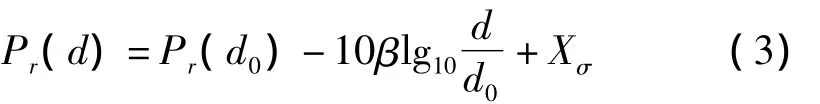
式(3)中，d0为参考距离;d为接收端到发送端的距离;Pr(d)为距离为d时接收端的平均接收功率;β为实际环境路径损耗因子，通常取值范围在2～6之间;Xσ为遮蔽因子，均值为0，均方差为 σ的正态随机变量。

Shadowing模型描述了接收功率和信号传播距离的关系，通常接收端距离发射端越远，接收到的功率越小。一般情况下，接收端可直接读取相应的RSSI值，无需额外的硬件。

2.1.2 跳数水平修正

节点通信半径R范围内的节点跳数都是1跳，该跳数并不能较好地反应出节点间实际距离大小关系，由此产生较大的测距误差。本文根据接收到的邻居节点RSSI值对每一跳进行分段细化，有助于提高节点定位精度。

假设节点通信半径为R，将水平修正跳数h按照相邻节点间实际距离L划分成n段，其中n的取值为2k，i为实际距离L所对应的分段区间数。水平修正方式如下

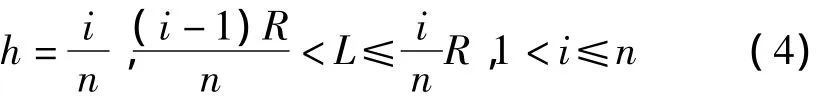
式(4)中相邻节点间实际距离L可以通过RSSI测距模型计算。然而，计算距离L会产生较大的计算量，节点的RSSI值可直接读取，将分段距离转换成相应的RSSI值可大幅降低计算量，可得式(5)和式(6)如下

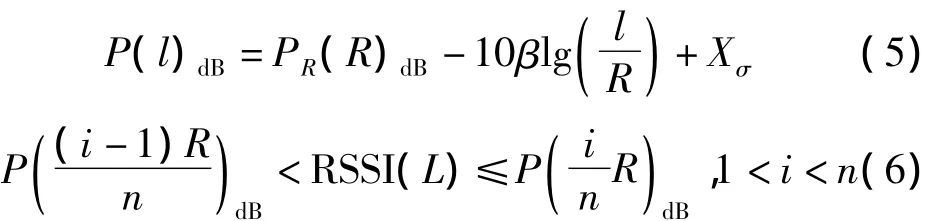
式(5)中，参考距离设置为节点通信半径R，可获取距离发射端L的接收功率P(l)dB;式(6)中，将各个分段距离代入式(5)获取各个分段的接收功率，比较接收节点获取的RSSI(L)值，可获取对应的分段区间数i，代入式(4)便可获取水平修正跳数h。可制成分段区间对照表1，未知节点直接获取RSSI值后，从区间1开始依次查找比对表1中接收功率，获取对应的水平修正跳数，可减少修正过程中的计算量。

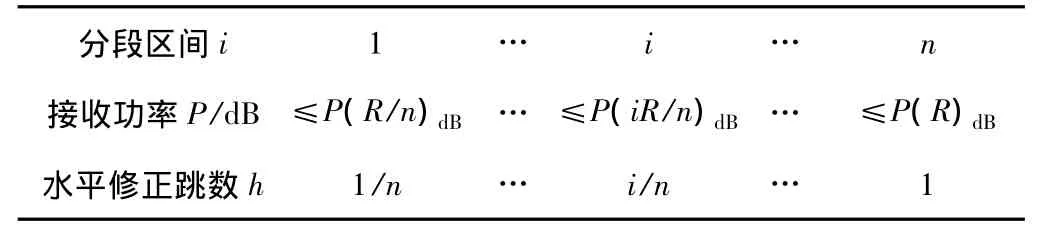
表1 分段区间对照表

水平修正后的跳数信息允许原DV－Hop算法1跳数量变成小数，并不一定是整数，可提高跳数信息的准确性，为垂直修正提供基础。

2.2 垂直修正

水平修正跳数后，只是修正了两节点间跳数，未能考虑到整个网络中节点分布相关联的可能情况，需进一步用来修正非相邻节点之间的跳数信息，如图2所示。

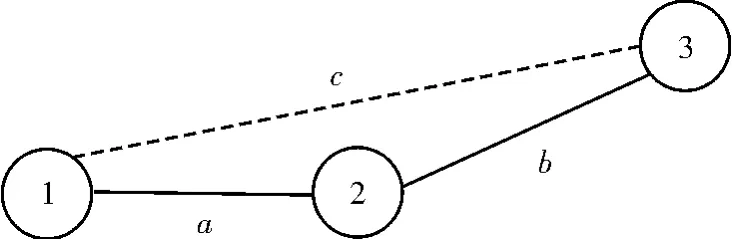
图2 节点垂直修正分布示意图

图2中，节点1和2之间的水平修正跳数为a，节点2和3之间的水平修正跳数为b，节点1和3之间的跳数c与a、b之和存在一定误差，引入a、b之间的修正夹角θ，经过垂直修正后，节点1和3之间的跳数c如下所示

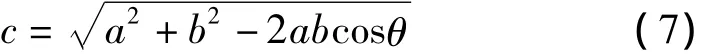
修正夹角θ的取值按照节点分布的概率取值，如图3所示，节点A和B是两圆圆心，两圆相距r，节点通信半径相同，均为R，即两圆半径，假设节点A通过节点B连通的节点为节点C，这节点C必定在图3阴影部分，同时，阴影部分上下两半是对称的，只需考虑上半部分即可。考虑到节点分布是随机的，所以，修正角度θ应该可以平分上半部分阴影区域面积。

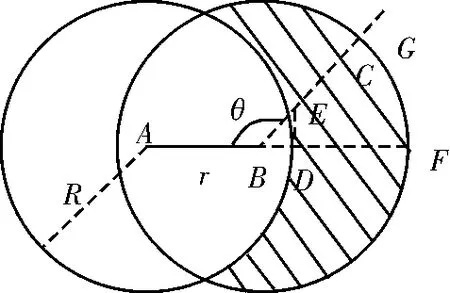
图3 修正夹角示意图

修正角度θ的计算方法如式(8)所示。式(8)中，S1/2为图3中阴影上半部分面积，可通过定积分求取，(π－θ)R2表示圆心角为(π－θ)的扇形BFG面积的2倍，(R－r)2tan(π－θ)为三角形BDE面积的2倍，此处计算取近似值，其中线段BF平分阴影区域面积，点F、G在圆上，线段ED为以A为圆心的圆切线，交BC与点E。

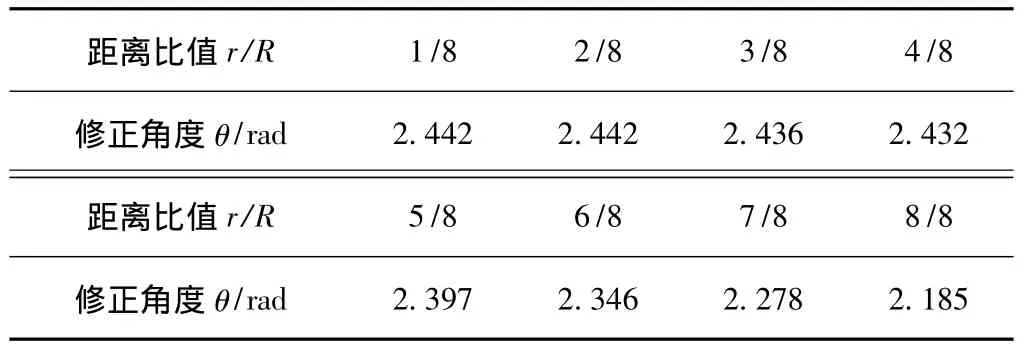
表2 修正角度对照表

r取值为iR/n，其中i为分段区间数，R为节点通信半径，n为分段数量。r/R的比值为i/n，取值对应水平修正跳数的分段区间。表2为r/R取值与修正角度θ的关系，其中分段数量n为8，修正角度单位rad。

接收节点根据发送节点的RSSI值，计算相应分段区间，获取距离比值r/R，通过查找表2，得到对应修正角度。

2.3 改进算法具体步骤

改进算法具体步骤如下:

(1)计算信标节点到其他节点的修正跳数。信标节点向邻居节点广播信息分组，每个节点维护一组信息表{Xi，Yi，Hi，hi}，其中(Xi，Yi)为信标节点 i的位置信息，Hi为原DV－Hop算法中的最小跳数，hi为修正跳数，Hi、hi初始值均为0。接收节点记录到每个信标节点的最小跳数Hi，忽略来自同一信标节点的较大跳数分组，此时跳数Hi加1，并对来自发送端的跳数进行水平及垂直修正，当然，对于Hi=1，即只有1跳的情况，只需进行水平修正，于此同时转发分组信息。通过这种方法，每个节点获得原DV－Hop算法中最小跳数的同时，也获得了最小跳数的修正值。

(2)计算未知节点到信标节点的实际跳段距离。每个信标节点需要获取平均每跳距离，按照式(1)计算即可，其中，hij不再是原算法中信标节点i，j的最小跳数，而是最小跳数的修正值;信标节点j广播平均每跳距离HopSizej，未知节点i收到该信息后，计算到信标节点j的实际跳段距离dij，如式(9)所示

其中，HopSizej是对应信标节点的平均每跳距离，不再是原算法中距离未知节点最近的平均每跳距离，这有助于在跳数修正的基础上提高定位精度;hj为未知节点到信标节点j最小跳数的修正值。

(3)利用三边测量法或极大似然估计法计算自身位置信息。未知节点获取至少3个到各个信标节点的跳段距离后，使用三边测量法或者极大似然估计法计算出自身的位置信息，其中获取3个跳段距离的使用三边测量法，3个以上使用极大似然估计法。

3 仿真实验

为验证基于跳数修正的改进算法的性能，采用Matlab 7.11.0进行仿真实验，对比改进算法与原算法的定位精度，并对仿真结果进行分析。

无线传感器网络的仿真环境如下:节点共100个;所有节点随机分布在100 m×100 m的正方形区域;正方形区域左下角为坐标原点(0，0)，右上角坐标为(100，100);信标节点与未知节点的通信半径相同且可调。为消除定位过程中节点随机分布产生的误差，仿真数据均为相同条件下运行100次的平均值。

无线传感器网络中定位精度是定位算法的一个重要指标，定位误差Error为

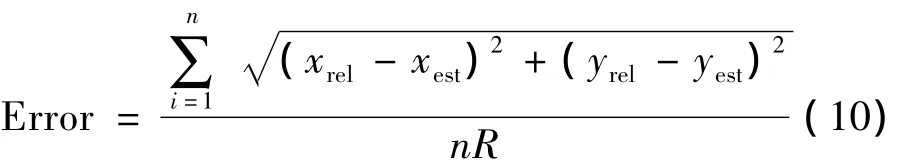
式(10)中，n为未知节点个数;R为节点通信半径;(xrel，yrel)为未知节点实际坐标;(xest，yest)为未知节点估计坐标。

在不改变节点总数的情况下，分3种网络情况进行仿真，与原算法进行比较:(1)信标节点比例不变，调整通信半径。(2)通信半径不变，调整信标节点比例。(3)固定信标节点比例，调整节点总数。

3.1 调整通信半径

在100 m×100 m正方形区域内，随机分布100个节点，信标节点比例为0.3，在其他条件不变的情况下，调整节点通信半径，对应通信半径与定位精度关系图，如图4所示，其中通信半径为R，n表示改进算法中水平修正分段数量。

如图4所示，随着通信半径的增加，DV－Hop算法、改进算法以及文献［9］算法的定位误差都呈下降趋势，改进算法的定位误差比原算法明显降低，尤其是改进算法中分段数量较大的情况下。通信半径为20 m时，通过仿真可发现，节点间最小跳数在3～8跳的比例为在70%左右，其中最小跳数最多的为6跳，由于节点随机分布造成情况复杂，造成改进算法、原算法、文献［9］算法的定位精度都不高;通信半径为25 m时，图4所示算法定位精度明显提高;通信半径达到30 m时，改进算法和原算法定位误差趋于稳定，改进算法(n=8)定位精度比原算法提高了约10%，相比文献［9］算法定位提高3%左右，改进算法(n=4)此时与文献［9］算法的定位误差还没有明显的区别，在随后半径增大的过程中才出现一定的差距。在趋于稳定的情况下，改进算法(n=8)的定位精度比改进算法(n=4)的定位精度高出约2%，表明增大分段数量有助于提高定位精度。可以看出，在其他条件不变的情况下，调整通信半径，改进算法(n=8)与原算法和文献［9］算法有明显的优势。

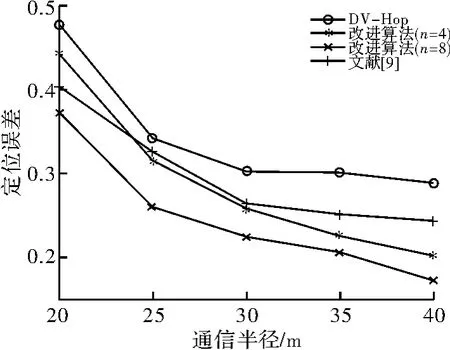
图4 通信半径与定位精度关系图

图5是改进算法(n=8)在调整通信半径过程中，将通信半径设为30 m时的定位误差图，节点位置随机分布，星号表示信标节点，空心圆表示未知节点位置估计值，直线表示未知节点位置估计值与真实位置的误差。如图5所示，未知节点在中心位置的估计误差比边缘位置小。

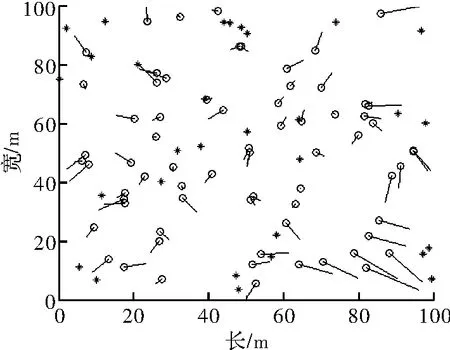
图5 改进算法(n=8，R=30 m)定位误差图

3.2 调整信标节点比例

同样在在100 m×100 m正方形区域内，随机分布100个节点，选取节点通信半径30 m，在其他条件不变的情况下，调整信标节点的比例Ratio，对应信标节点比例与定位精度的关系，如图6所示。

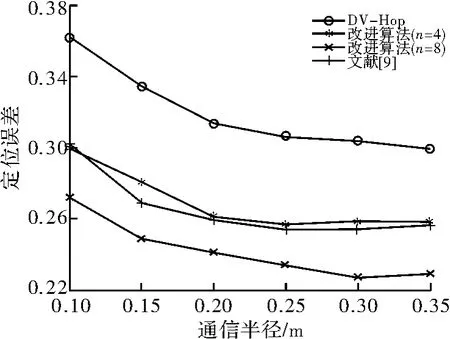
图6 信标节点比例与定位精度关系图

如图6所示，随着信标节点比例的增加，DV－Hop算法和改进算法的定位误差都呈下降的趋势，改进算法的定位误差比原算法明显低。信标节点比例达到0.2之前，改进算法、原算法以及文献［9］算法定位精度都不高，但随着信标节点比例的增加，定位精度明显。信标节点比例达到0.25时，改进算法、原算法以及文献［9］算法的定位误差趋于稳定，此时，改进算法(n=4)的定位精度比原算法提高了约5%，与文献［9］算法定位精度相当，改进算法(n=8)的定位精度比原算法提高约8%。改进算法中分段数量由4增加到8时，定位精度同样提高3%左右，分段数量的增加在此情况下也有助于提高算法的定位精度。所以，在只调整信标节点比例的情况下，改进算法(n=8)与其他算法相比，也有较大的优势。

图7是改进算法(n=8)在调整信标节点比例过程中，将信标节点比例设为0.25时的定位误差图，星号表示信标节点，空心圆表示未知节点位置估计值，直线表示未知节点位置估计值与真实位置的误差。由图7可看出，处于中心位置的未知节点估计误差较小。

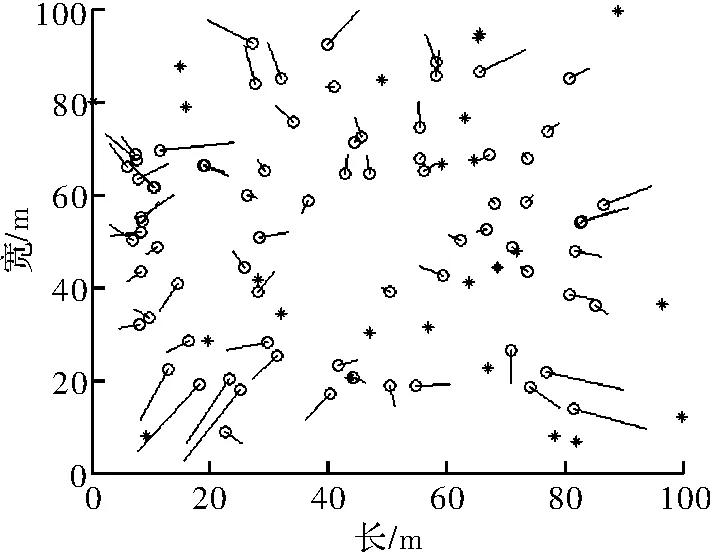
图7 改进算法(n=8，Ratio=0.25)定位误差图

3.3 调整节点总数

同样在100 m×100 m正方形区域内，随机分布N个节点，信标节点比例设为20%，选取节点通信半径30 m，在其他条件不变的情况下，调整节点总数N，对应节点总数与定位精度图，如图8所示。

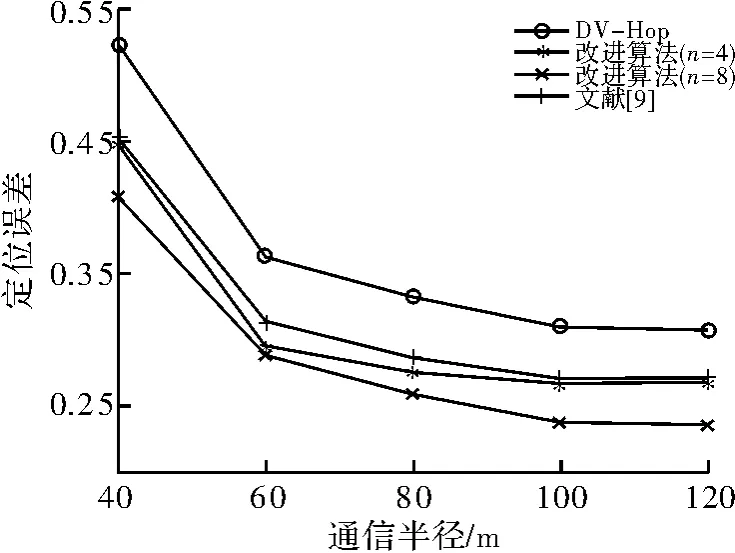
图8 节点总数与定位精度关系图

如图8所示，随着节点总数的增加，DV－Hop算法和改进算法的定位误差都不断减小。节点总数较小时，改进算法、原算法以及文献［9］算法定位精度都不高，但是随着节点总数的增加，定位精度提升明显。节点总数在80个以上时，改进算法、原算法以及文献［9］算法的定位误差趋于稳定，此时，改进算法(n=4)的定位精度比原算法提高了约4%，与文献［9］算法定位精度相当，改进算法(n=8)的定位精度比原算法提高约7%。改进算法对于原算法有明显优势，同时，改进算法(n=8)相比文献［9］算法有较大优势。

图9是改进算法(n=8)在调整节点总数过程中，将节点总数设为80时的定位误差图，星号表示信标节点，空心圆表示未知节点位置估计值，直线表示未知节点位置估计值与真实位置的误差。从图9也可得出图5和图7中的结论，中心处的未知节点估计误差较小。

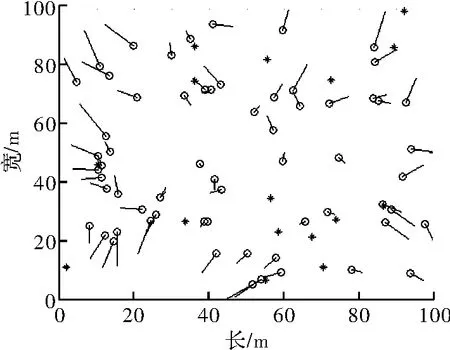
图9 改进算法(n=8，N=80)定位误差图

3.4 改进算法分析

通过上述3种网络情况的分析可看出，改进算法的定位精度与原算法相比有明显提高。改进算法在水平修正过程中的分段数量也影响着定位精度的提高，一般情况下，分段数量越多，跳数信息所反映的节点间距离关系越准确，定位精度越高。

同时，改进算法对跳数进行水平及垂直修正，修正的过程中引入查找表，大幅减少了修正过程中的计算量，与原算法相比，计算量增加不明显。改进算法的通信量与原算法相当，并未给原算法增加额外通信开销。

4 结束语

针对传统DV－Hop算法中跳数信息不能反应节点间实际距离关系而导致较大定位误差的问题，提出一种水平及垂直修正跳数的改进算法。改进算法首先将相邻节点跳数细化，并在分析两节点距离和可能分布情况的基础上，对不相邻节点引入修正角度，两者结合，使修正跳数尽可能反应节点间实际距离关系。改进算法在定位过程中引入查找表，较好地降低了改进算法的计算量，而且改进算法也并未增加通信开销。仿真结果表明，改进算法较好地提高了传统DV－Hop算法的定位精度。下一步需要研究边缘位置的未知节点定位情况，提高边缘位置的定位精度。

［1］Akyildiz I F，Su W，Sankara Subramaniam Y，et al.Wireless sensor networks:a survey［J］.Computer Networks，2002，38(4):393－422.

［2］He T，Huang C，Blum B M，et al.Range － free localization schemes for large scale sensor networks［C］.Proceedings of the 9th Annual International Conference on Mobile Computing and Networking，ACM，2003:81 －95.

［3］林金朝，陈晓冰，刘海波.基于平均跳距修正的无线传感器网络节点迭代定位算法［J］.通信学报，2009(10):107－113.

［4］Wu H，Gao R.An improved method of DV －hop localization algori－ thm［J］.Journal of Computational Information Systems，2011，7(7):2293 －2298.

［5］周小波，乔钢柱，曾建潮.无线传感器网络中基于 RSSI的加权 DV－HOP定位方法［J］.计算机工程与应用，2011，47(14):109－111.

［6］杨祥，潘玮.基于RSSI比值修正的无线传感器网络DVHop定位算法［J］.传感器与微系统，2013，32(7):126－128.

［7］Deng Yin Z，Guo Dong C.A union node localization algorithm based on RSSI and DV － Hop for WSNs［C］.International Conference on Instrumentation，Measurement，Computer，Communication and Control(IMCCC)，IEEE，2012:1094 －1098.

［8］温江涛，范学敏，吴希军.基于 RSSI跳数修正的 DVHop改进算法［J］.传感技术学报，2014(1):113－117.

［9］方海涛，雷菁，胡昆明，等.基于 RSSI修正的改进 DVHop测距算法［J］.通信技术，2012，45(2):16 －18.

［10］Du W，Deng J，Han Y S，et al.A pairwise key predistributionscheme for wireless sensor networks［J］.ACM Transactions on Information and System Security(TISSEC)，2005，8(2):228－258.

［11］He T，Huang C，Blum B M，et al.Range － free localization schemes for large scale sensor networks［C］.Proceedings of the 9th Annual International Conference on Mobile Computing and Networking，ACM，2003:81－95.