北斗接收机空时联合抗干扰算法研究

姚 锐

(西安电子科技大学电子信息攻防对抗与仿真重点实验室，陕西西安 710071)

作为全球导航卫星系统(Global Navigation Satellite System，GNSS)的一部分，射频干扰信号是北斗系统的最大威胁，如何正确评估干扰信号对导航接收机捕获性能的影响成为抗干扰研究的前提［1］。传统盲自适应抗干扰算法，如功率倒置(PI)算法，受到自由度的限制，当干扰数较多时，需要增加天线数，这对北斗接收机是不现实的，另外纯空域滤波无频率分辨率，当有用信号和干扰来自同一方向时，北斗接收机无法做到只抑制干扰而保留有用信号。

本文介绍了空时联合抗干扰(STAP)算法，空时联合算法克服了单纯空域抗干扰技术的不足，它在不增加阵元的前提下，通过时间抽头大大增加了自适应天线阵列的自由度，在增加可处理干扰数目的同时增强了对宽带干扰和窄带干扰的抑制能力。空时联合处理在抑制干扰时有以下特点:(1)如果阵元个数为M，空时处理由于自由度的增加，可以产生大于M个的零陷，抑制＞M个的干扰。它抑制宽带干扰的效果和数量随时域滤波器阶数增加而改善。(2)空时处理可以抑制两种特殊情况下的干扰。1)干扰信号为窄带干扰，入射源与某颗卫星方位相近，甚至可以同方向。由于空时处理已将输入信号划分为窄带信号处理，消除窄带干扰时零陷不会削弱带外的卫星信号。2)干扰信号为宽带信号，入射方向与某颗卫星方位较近(约10°)，但不能同方向。这是由于空时处理形成的方向图是空频域的，不同于空域方向图，阵面波束宽度有限，零陷的过渡角会削弱附近卫星信号。

1 STAP算法原理

空时联合处理的基本思想是在天线阵列后加上若干个延迟单元，延迟单元相当于频域滤波器，可以在频域上对干扰进行抑制［2－4］。

假设一均匀线阵，天线个数为M，延迟单元数为P，时延间隔为T，空时联合抗干扰的基本框图如图1所示。

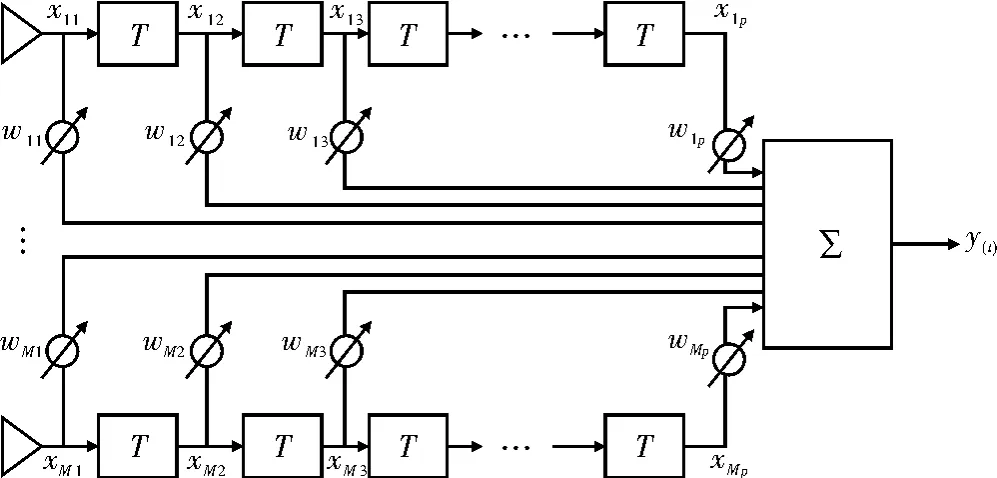
图1 空时联合抗干扰处理的结构图

当接收信号入射到阵列上时，第m个阵元的第p个抽头接收到的信号为

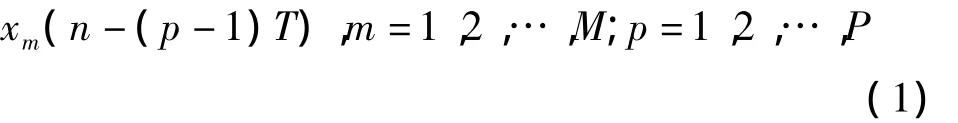
式中，M为阵元数;P为每个天线的延迟单元数;T为每个抽头的时延，要求T＜1/B，B是信号带宽。设第m个阵元的第p个抽头的权值为wmp，则滤波器的输出为

若写成矩阵形式为

式中

由此可以看出，空时联合处理是空域天线阵列在时域上的扩展，相当于在不增加天线数的前提下增加了滤波器的自由度，从而能比单纯的空域滤波滤除更多干扰，这里将W和X表示为

当角频率为ω的信号以方向θ入射时，第m个阵元的第p个抽头接收到的信号可表示为

其中

d为阵元间的间隔，λ为入射信号波长，则相应的空时二维导向矢量为

其中⊗为科洛内克积

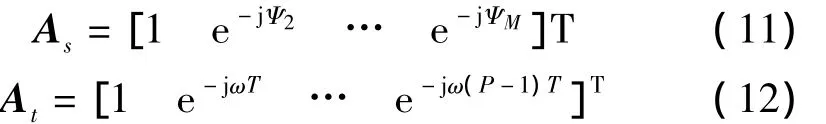
As为空间导向矢量，At为时间导向矢量。由此可见，空时处理的自由度，由空间自由度和时间自由度构成，其数量为M×P。空时处理对处理宽带信号的特点是:时间上延迟P阶，在频域上相当于将整个处理带宽对频率均匀分成P段，如果频率段分得足够细，每一个频率段可以近似于单频信号频率进行处理。所以空时处理就是利用时间延迟增加时间自由度，将宽带信号的处理转变为对多个窄带信号的处理。所以，P的大小影响着空时处理消除宽带干扰的性能。

根据如图1所示的空时联合抗干扰处理的结构，在进行算法仿真时，不能直接使用天线接收到的数据，而是要对输入数据进行分段处理，转换数据的排列格式，假设均匀线阵阵元数为M，每个天线单元接收到的快拍数为L，时域滤波器延迟单元数为P，那么空时二维快拍数则为L－P+1，分段后的接收数据矩阵可表示为［5］

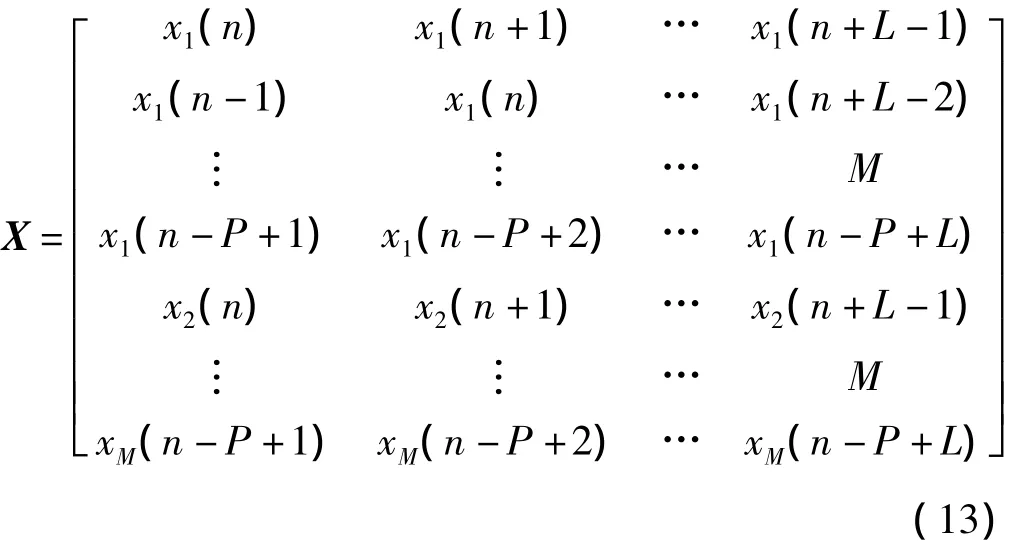
在约束条件下，根据线性约束最小方差(LCMV)准则，关于W的最优化问题可描述为

其中，R=E［XXH］是输入信号的协方差矩阵，为MP×MP 维。S=［1，0，…，0］T为 MP ×1 维，利用拉格朗日乘子法可以推导出最优空时处理的解为

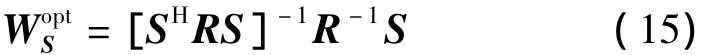
2 空时算法仿真结果

仿真在同一基本条件下进行，在考虑各参数对仿真结果的影响时，只改变相应参数，而基本仿真条件保持不变。假设均匀线阵阵元数为M，每个天线单元接收到的快拍数为L，时域滤波器延迟单元数为P，那么，空时二维快拍数则为L－P+1。

仿真条件:阵元形式为均匀线阵;阵元间距d为中心频率半波长;有用信号参数:信噪比－20 dB，为经PRN码调制后的扩频信号，方向角为0°;3个干扰信号的参数:两个宽带干扰，其中一个频率覆盖整半个个带宽，宽带干扰的干噪比为40 dB，方向角为－20°;另一个为频率覆盖范围为1/10带宽，干扰的干噪比为30 dB，方向角为40°;一个窄带干扰，干噪比为50 dB，方向角为20°;噪声为高斯白噪声;天线接收快拍数N=400。仿真图三维坐标分别为归一化频率、来波方向和归一化增益，其中，归一化频率为信号频率减去中心频率再除以带宽。

固定阵元数M=4，改变延迟单元数P，对于每种情况，都用两个仿真图加以说明，图(a)为三维图;图(b)是以归一化频率和来波方向这两个坐标确定的平面图，颜色条上不同的颜色代表增益的大小。

3 结束语

当P=1时，为纯空域滤波情况，此时由于有充足的空间自由度，不论是宽带干扰还是窄带干扰，只要有干扰的方向均形成较深的零点，如图2所示。此时，系统只能对干扰在空间上加以区分，没有时域滤波作用，若有用信号方向与干扰方向相同，即便频率不同，也会受到抑制，而无法只抑制干扰而保留有用信号。

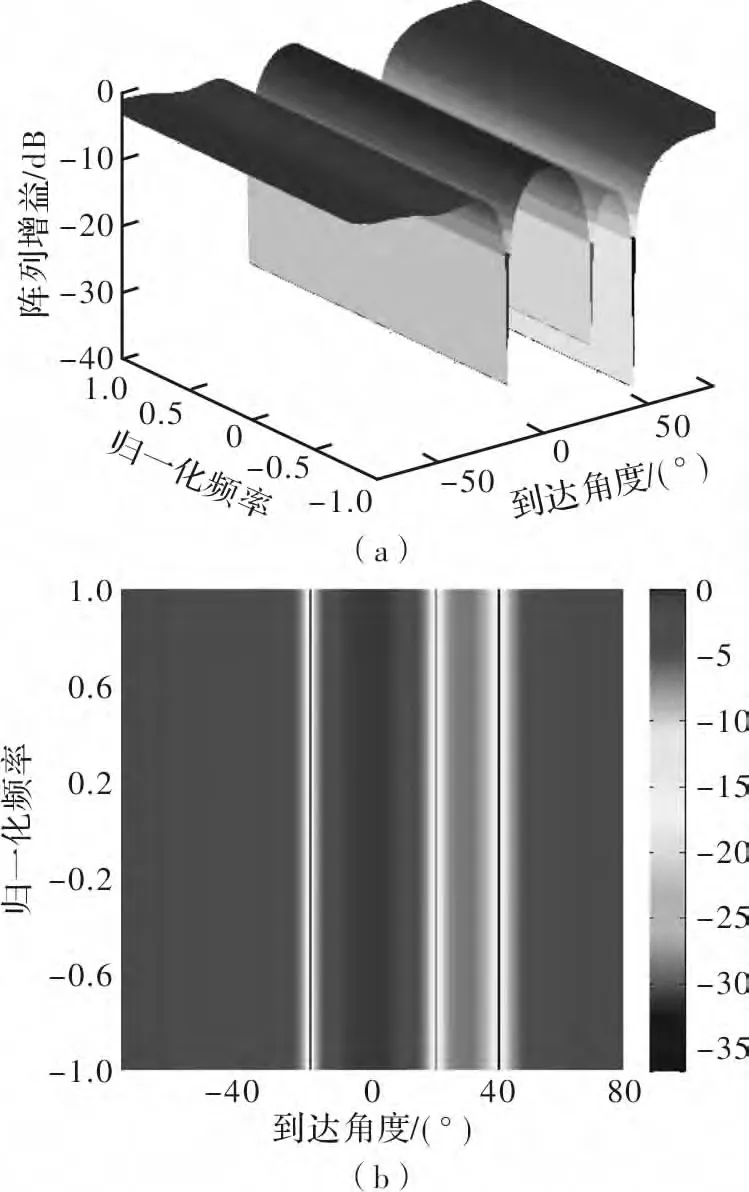
图2 抽头数P=1仿真结果

当P=3时，由于有频率分辨能力，此时对于窄带干扰，可以在空域和时域上同时进行抑制。但如图3所示，由于时域延迟数较小，部分频带干扰所形成的零点仍然占据了整个带宽，对干扰的频域分辨能力率明显不足，此时即便有用信号与单频干扰在同一方向，只要频率不同，也可以只对干扰进行抑制，而正确接收有用信号。

当P=8时，由于延迟数增大，频率分辨率越来越高，窄带干扰形成的零点也逐渐变窄，而部分频带干扰所形成的零点范围也越来越接近其真实频率范围，如图4所示。仿真结果表明，空时联合抗干扰算法能够利用空域和时域的特性，在不增加阵元的情况下有效地抑制宽带和窄带干扰。

图3 抽头数P=3仿真结果

图4 抽头数P=8仿真结果

［1］张宏雷.干扰信号对北斗接收机的性能影响评估［J］.消费电子，2013(6):1－3.

［2］Kohko R.Spatial and temporal communication theory using adaptive antenna array［J］.IEEE/ACM Personal Communications－The Magazine of Nomadic Communications and Computing，1 998(2):28 －35.

［3］Jtm S，Iltis R A.STAPfor GPSreceiver synchronization［J］.IEEE Transaction on Aerospace and Electronic Systems，2004，40(1):251 －256.

［4］Goldstein J S，Guerci J R，Reed I S.Advanced concepts in STAP［C］.IEEE International Radar Conference Alexandria，VA，2000:699 －704.

［5］项建弘.基于空时自适应处理的GPS调零技术应用研究［D］.哈尔滨:哈尔滨工业大学，2008.