基于小波变换的MSK信号码速率盲估计

郜宪锦

(西安电子科技大学电子信息攻防对抗与仿真技术教育部重点实验室，陕西西安 710071)

MSK(最小频移键控)调制是数字通信中一种连续相位的频移键控调制方式［1］，具有传输带宽小、包络稳定、功率谱性能好、频带利用率高等优点，并且具有较高的抗噪声干扰能力，因而被广泛应用于通信中。随着MSK信号的广泛应用，其参数估计越来越受到重视，其中码速率作为调制信号的重要参数，需要进行精确估计。

MSK调制信号不存在相位跳变，因此通过两次小波变换估计FSK信号码速率［2］和通过小波变换直接检测相位跳变来估计MPSK信号码速率［3］的方法不能用于估计MSK信号的码速率。文献［4］对MSK信号延迟乘以自混频信号过低通滤波器，得到的基带信号跳变位置，受延迟时间的影响，导致码速率估计存在误差。针对上述问题，本文利用信号频差与码速率的关系，粗估计MSK信号码速率，以此为参考选取短时傅里叶变换窗函数长度和小波尺度，对通过STFT得到的信号瞬时频率序列［5］进行小波变换，而后对变换后的结果进行频谱分析估计MSK信号码速率。仿真结果表明，这种方法在无先验信息的条件下可以对码速率进行盲估计。

1 MSK码速率估计

MSK信号的解析表达式为

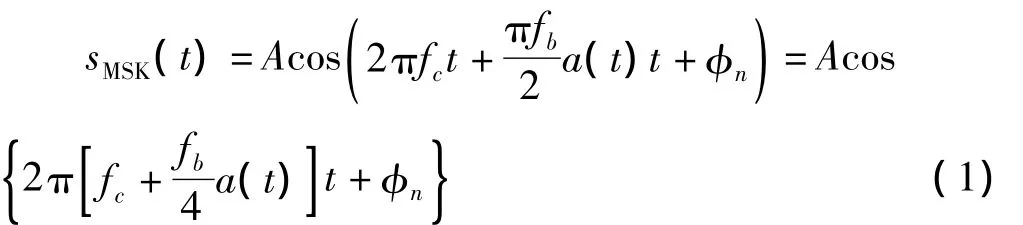
式中，A为信号幅度;a(t)为信息码元序列±1，fc取值为;fb为信号载频;φn是信号的码速率;为各个码元对应的初始相位。MSK信号频谱如图1所示。

将接收信号进行短时傅里叶变换(STFT)，估计出信号的瞬时频率变化。

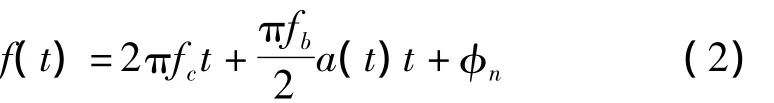
图1 MSK信号频谱

如图2所示，瞬时频率序列在码元相位跳变处有拐点，此时可利用Haar小波的边缘检测特性检测相位跳变点。

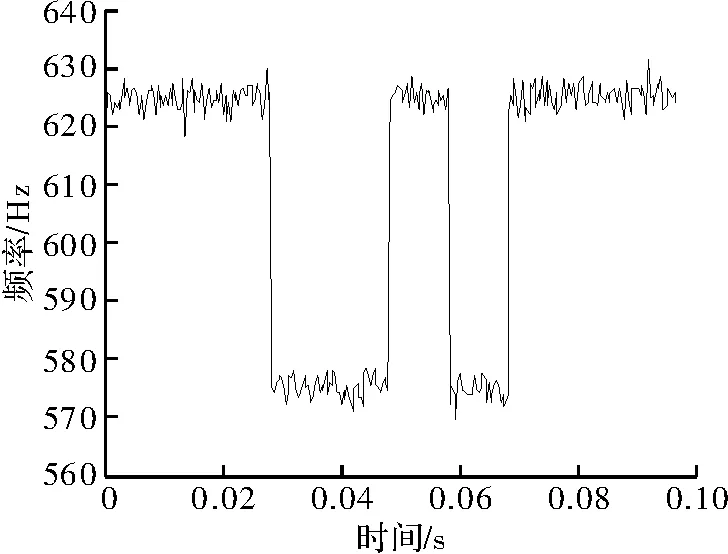
图2 MSK信号瞬时频率变化

z(t)的小波变换为

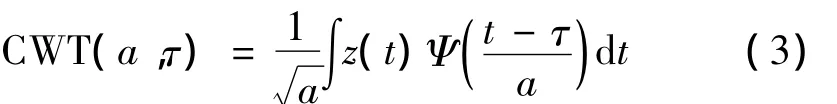
式中，Ψ(t)为母小波函数，a为伸缩尺度，τ为平移因子。

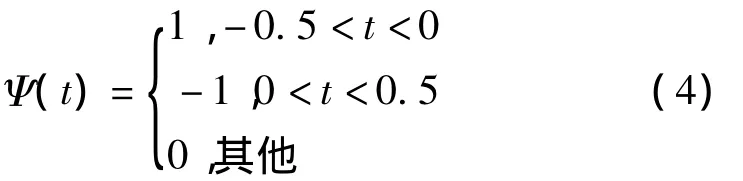
当Haar小波在一个码元周期内，若此时编码a(t)=1则

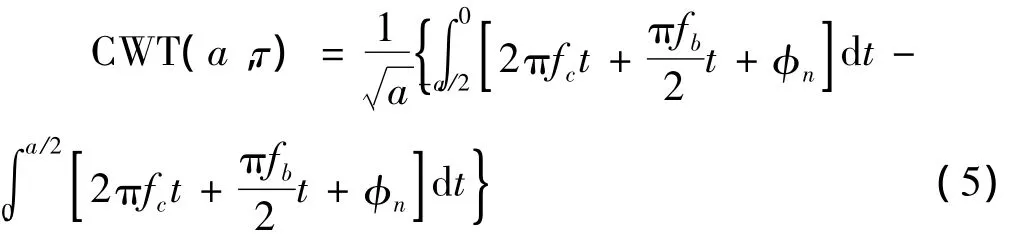
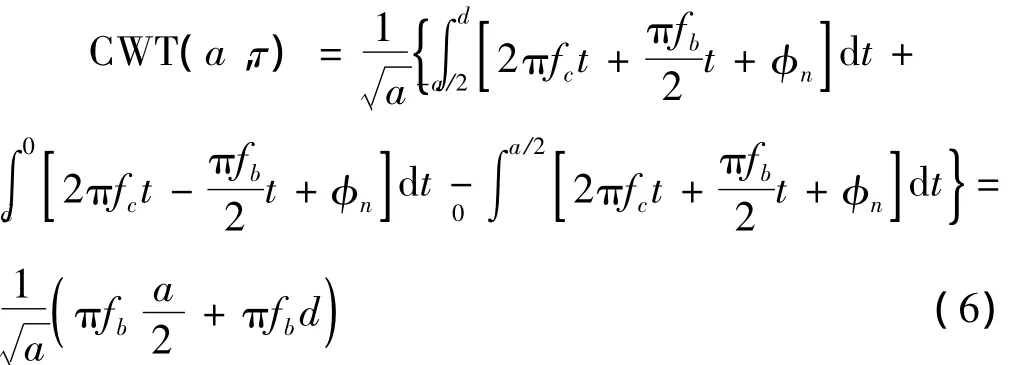
当Haar小波跨越相位跳变处时，则式中，d为Haar小波中心与相位跳变点的距离，由于d＜0，因此当d=0即Haar小波中心处于相位跳变点时最大。文献［3］对相位编码信号码速率盲估计算法中小波系数的选取进行了论述，结合其最佳选取系数a，通过对MSK调制信号的码速率进行粗估计，作为小波尺度的选取参考

式中，Tb为信号的码元宽度。另外，在没有先验知识的条件下，应用多尺度分析可以有效减少噪声对估计的影响，选取0.4/fb，0.6/fb和0.75/fb3个小波尺度，对不同尺度小波变换结果叠加得到的序列进行傅里叶变换，利用其频谱最高谱线估计对应频率，此频率对应f(t)信号最小码元宽度即为MSK信号的码速率，如图3所示。

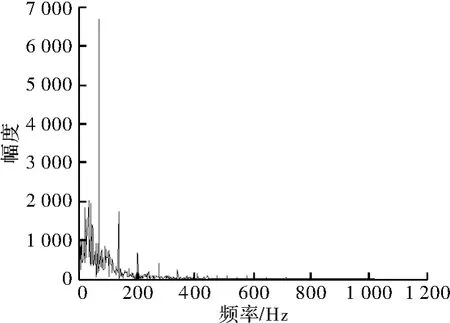
图3 小波变换后序列的频谱

2 短时傅里叶变换窗函数长度的选取

实际的相位编码序列千变万化，要结合公式定量分析短时傅里叶变换窗函数长度同码速率估计的关系存在一定困难。当窗函数包含的频率变化信息过多时，通过短时傅里叶变换得到瞬时频率变换将无法正确反映信号真实的频率变化，引起码速率估计误差，本文结合仿真方法分析并选取较合适的短时傅里叶变换的窗函数长度。

最小频移键控(MSK)调制的频差需要满足两个频率相互正交，结合其表达式可知，频差Δf=fb/2。因此，可通过对信号进行傅里叶变换，得到信号的频谱，如图1所示。通过对信号频谱谱线的检测，得到信号频谱的两个谱峰位置，两谱峰对应频率差值的2倍即为信号的码速率，通过粗估计的码速率来确定短时傅里叶变换窗函数的长度。

如图5所示，对MSK调制信号的码速率粗估计的精度不高，但可以作为短时傅里叶变换窗函数的选取参考。由仿真分析可知，选取短时傅里叶变换窗函数长度 l≈时具有较好的性能。

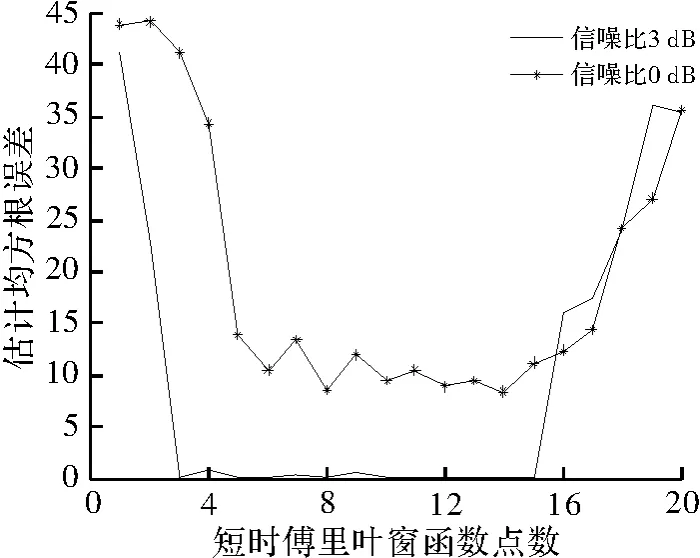
图4 STFT窗函数长度对估计性能的影响

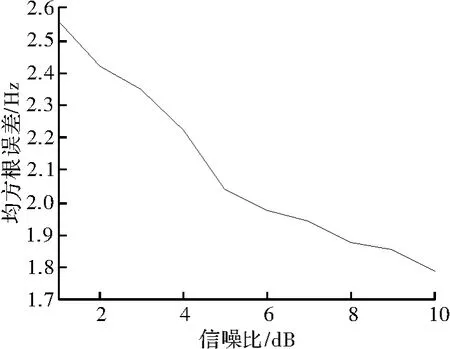
图5 码速率粗估计的误差分析

3 算法实现

对最小频移键控(MSK)调制的码速率估计步骤如下:

步骤1 对接收信号作FFT，分析其频谱谱线，得到两谱峰的频差Δf。

步骤2 由频差粗估计信号的码速率fb=2Δf，并选取短时傅里叶窗函数的长度l=0.5/fb以及3个伸缩因子 a1(a1=0.4/fb)，a2(a2=0.6/fb)，a3(a3=0.75/fb)。

步骤3 对MSK调制信号进行STFT变换得到其瞬时频率序列f(t)。

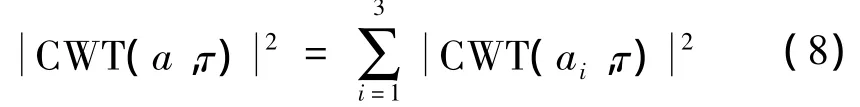
步骤5 对叠加结果作FFT，滤除直流分量后，估计出峰值谱线所对应的频率fmax。

步骤6 得到最小频移键控(MSK)调制的码速率估计fb=fmax。

4 仿真分析

对文中算法进行Matlab仿真，并结合文献［4］所给的方法进行比较。仿真参数为:采样频率为3 kHz，信号载频为600 Hz，码速率为 100 Byte·s－1，随机产生300个码元编码，另外仿真噪声为与信号相互独立的高斯白噪声，以与真实码速率的相对误差＜0.1%作为正确估计［6］。在不同信噪比条件下进行的蒙特卡罗试验次数为100，得到不同信噪比下的码速率估计性能。文献［4］的算法需要对MSK信号延迟相乘得到自混频信号，由于延迟时间将码元跳变点改变为自混频信号的相位渐变，在用小波变换检测边缘特性时，得到的跳变点可能出现偏差，导致码速率估计误差较大。结合与文献［4］的估计性能比较，误差一致的情况下本文算法的抗噪声能力明显较强。

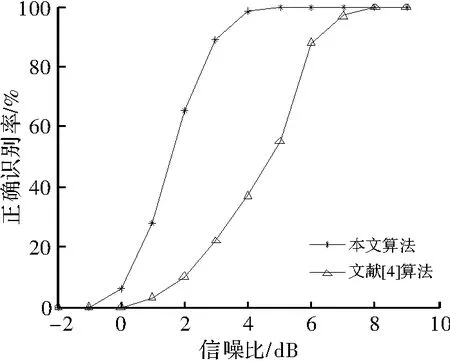
图6 算法仿真结果

5 结束语

结合理论分析与仿真结果可以看出，本文所提方法在较低信噪比下对码速率可以进行有效估计。并且通过对信号频谱分析，得到码速率粗估计值作为算法短时傅里叶变换窗函数长度以及小波尺度的选取参考。通过选取值对信号进行短时傅里叶变换得到信号瞬时频率序列，然后用不同的小波尺度对得到的瞬时频率序列进行相位跳变检测，最后将检测结果进行频谱分析，以频谱最大值对应的频率作为码速率估计。本算法无需获取信号先验信息即可进行码速率估计，在情报获取和无源探测等场合具有应用价值。

［1］David Gidony，Irving Kalet.Adjacent channel interference cancellation for MSK－type signals using antenna diversity in rayleigh fading environment［J］.IEEE Transactions on Communications，2004，52(2):317 －325.

［2］王晓娜.典型通信信号调制识别技术研究［D］.成都:电子科技大学，2011.

［3］邓振淼，刘渝.基于多尺度Haar小波变换的MPSK信号码速率盲估计［J］.系统工程与电子科技，2008，3(1):36 －40.

［4］郑文秀.MSK信号的参数估计［J］.电路与系统学报，2011，16(2):23 －27.

［5］生成春，赵辉.基于瞬时频率谱的码元速率估计方法［J］.电气电子教学学报，2010，31(1):50 －54.

［6］罗明.数字通信信号的自动识别与参数估计研究［D］.西安:西安电子科技大学，2005.