小波滤波在变形分析中的应用

王亚宾

摘要：受仪器精度、测量环境等影响，监测成果经常含有噪声甚至粗差，不利于稳定性判断或变形分析。本文利用小波滤波对变形数据进行滤波处理，并采用能量比（SER）与噪声模（NM）以及光滑性和相似性等准则进行滤波效果评价，得到了较好的效果。

关键词：变形监测；变形分析；小波滤波；滤波效果评价；GPS测量

1.概述

滤波是将信号中特定波段频率滤除去的操作，是抑制和防止干扰的一项重要措施；也是根据观察某一随机过程的结果，对另一与之有关的随机过程进行估计的概率理论与方法。变形分析中的滤波简单之即为剔除或减少观测数据中的噪声（误差），获取较为真实的变形过程。

由于小波具有良好的“时间（空间）-频率”特性，它被广泛地应用于信号处理、图像处理、量子场论、地震勘测、话音识别与合成、音乐、雷达、CT成像、彩色复印、流体湍流、天体识别、机器视觉、机械故障诊断与监控、分形及数字电视等科技领域。在小波分析中，应用最广泛的无疑是信号处理和图像处理，而在这两个领域应用最多的就是信号（图像）滤波后和压缩。由于正交小波中，正交基的选取比传统方法更接近实际信号本身，所以通过小波变换可以更容易地分离出噪声或其他我们不需要的信息，因此在这类应用中小波分析有着传统分析方法无可比拟的优势。

图1显示了小波滤波和粗差探测的效果，a是一个被加性白噪声污染的信号，b为其对应的滤波后的信号；c是在a中的第400个分量模拟了一个粗差，d为其对应的滤波后信号。从该图可以看出，利用小波分析不仅能很好的分离出噪声，而且能够准确地探测出粗差。

对于离散的观测序列值（信号），如各种变形监测点的离散观测序列，由于受观测环境、仪器精度等影响，也可能存在噪声甚至粗差，可利用小波变换对这类信号进行滤波分析，以剔除噪声并探测粗差。

2.小波滤波

2.1小波滤波方法

小波分析以小波变换为基础。与傅里叶变换（基均为正弦函数）不同的是，小波变换的基不是唯一的，所有满足小波条件的函数都可以作为小波函数。常用的小波函数（或变换）有Haar小波、Daubechies小波、SymletsA（symN）小波系等。图2和图3分别表示了信号与噪声的离散小波变换；其中，最上方分别为某信号f和高斯白噪声g，往下依次是在四个尺度上对应的小波变换。比较两图，可以看出：信号的小波系数在每个尺度上都有反映，而噪声的能量却集中在小尺度上，其小波系数的幅值随着尺度的增加而迅速衰减。

小波滤波，就是利用具体问题的先验知识，根据信号和噪声的小波系数在不同尺度上具有不同性质的机理，构造相应规则，在小波域采用一定的数学方法对含噪信号的小波系数进行处理。处理的实质在于减小甚至完全剔除由噪声产生的系数，同时最大限度地保留真实信号的系数，最后由经过处理的小波系数重构原信号，得到真实信号的最优估计。其中，“最优”是依赖于应用的要求。

由于信号和噪声在不同尺度上有不同的特征表现，基于这一原理，发展出了不同的滤波方法，主要有模极大值重构滤波、空域相关滤波和小波阈值滤波等，近年来基于提升小波理论发展而来的提升小波滤波方法也得到了较多的应用。不同的滤波方法具有不同的特点，适应的信号也不尽相同，表1为上述滤波方法的定性比较，实际应用时可根据信号特点进行灵活选择。

2.2小波滤波效果的评价

小波滤波方法很多，如何评价滤波的效果，是滤波分析的一个重要环节。常用的评价方法包括：均方根误差（RMS，即滤波后信号与原信号较差即噪声的均方根，简称均方根误差，反映了滤波后信号与原信号间的相似程度）、信号偏差（BLAS，为滤波后信号与原信号之间的偏差，其实质是噪声的算术平均值）、信噪比（SNR，滤波后信号能量与噪声能量的比值）和信噪比增益（GSNR，滤波后的信噪比与滤波前的原信噪比的比值）。

均方根误差RMS、信号偏差BLAS、信噪比SNR和信噪比增益GSNR都是从噪声的角度来评价滤波的效果，其中均方根误差RMS和信号偏差BLAS是直接考虑噪声本身，而信噪比SNR和信噪比增益GSNR是根据噪声与信号的能量比及其变化。由于噪声的未知性，使用这些方法就难以对滤波效果作出正确的评价。为此，针对变形监测数据特点，笔者提出以下评价指标：

（1）信号能量比（SER）与噪声模（NM）：滤波后信号能量与原信号能量之比，它反映了滤波后信号与原信号间的相似程度；噪声模即噪声的模或能量，它反映了“噪声”的总体水平。

（2）光滑性与相似性：光滑性和相似性是信号滤波后的两条重要准则。其中光滑性是指大部分情况下，滤波后信号应该至少和原信号具有同等的光滑性；相似性是指滤波后信号和原信号较差的方差估计应该在最坏情况下的最小。光滑性一般可通过滤波前后的信号曲线直接判斷；相似性在计算上比较困难，一般也可通过比较滤波前后的曲线进行判断，要求滤波后信号曲线要整体上保持与原信号相同的特点：信号过程、信号强度、信号趋势，以及信号的特征点（如拐点）等。

信号能量比SER可按测量中通用的3σ（或2σ）原则进行评价，即SER>99.7%（或95.0%）时，认为滤去的都是噪声；换言之，从能量的角度，可认为噪声为小概率事件。以此为前提，认为剔除的噪声越多越好，即NM值越大越好。噪声模NM还通过以下方式进行定量检查：

设f=f（i）（i=1，2，…，n）为由n个测量值组成的信号序列，其测量误差为σ0，由误差传播率，该信号序列的误差为σ=mσ0n（m=1，2，3，…），以此为限差，可对噪声模NM进行定量检查。

因此，信号能量比SER和噪声模NM都具有实际意义，并且都能从定量的角度进行检查。信号能量比和噪声模是从定量的角度来评价滤波效果，而相似性和光滑性两条准则是从图形的角度来评价滤波效果，是一种定性的方法，将这两者结合起来，就形成了从定性到定量、从信号到噪声的全面、综合的滤波效果评价方法。

3.应用分析

（1）应用一

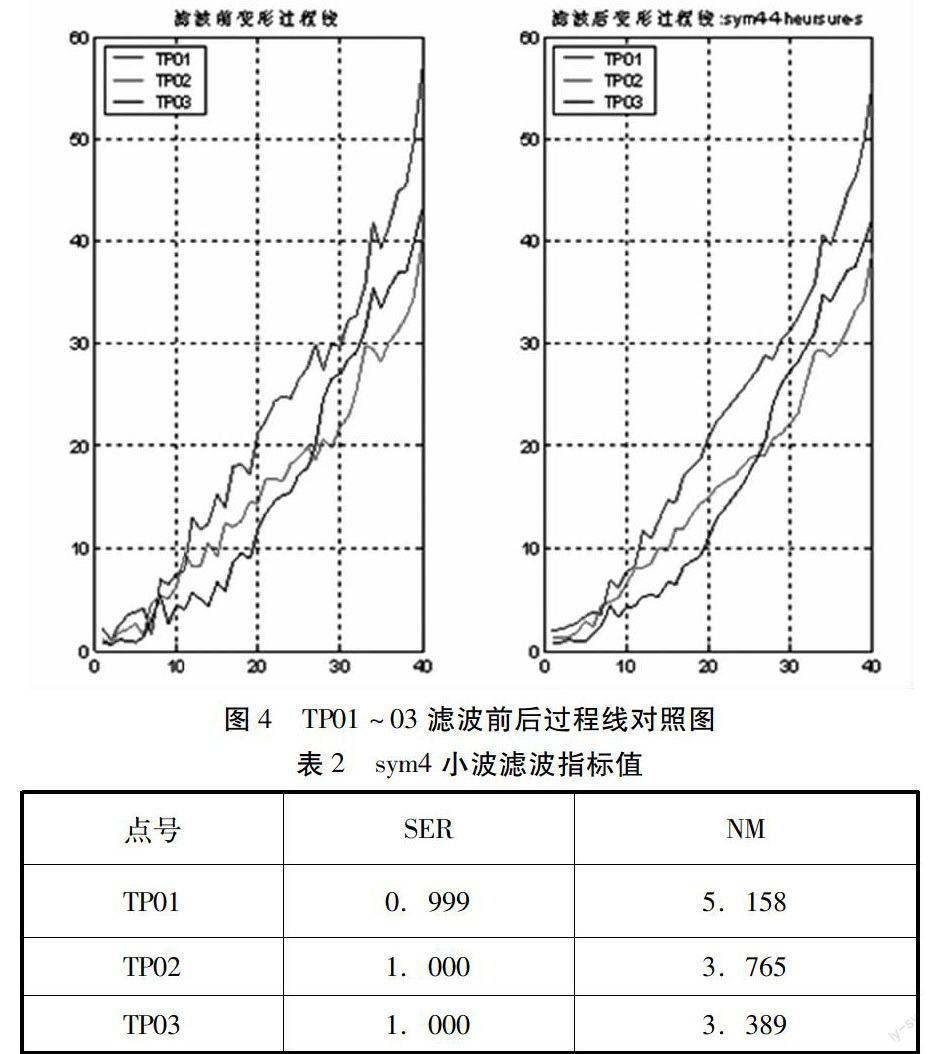
某边坡布设有AL02C、AL03C和TP01～TP11共13个监测点，平面监测精度为9mm。利用sym4小波对其中的3个点TP01～TP03累计40期平面监测数据进行滤波分析，分析結果如图4所示，对应的指标值如表2所示。

从表2可以看出，滤波后的信号能量比（SER）很高，几乎都达100%，而噪声模（NM）都较小。再结合图4，滤波后的曲线不仅很好地满足相似性和光滑性两条准则，而且特征点（拐点）更突出，可以很清晰的看出变形过程和变形趋势。

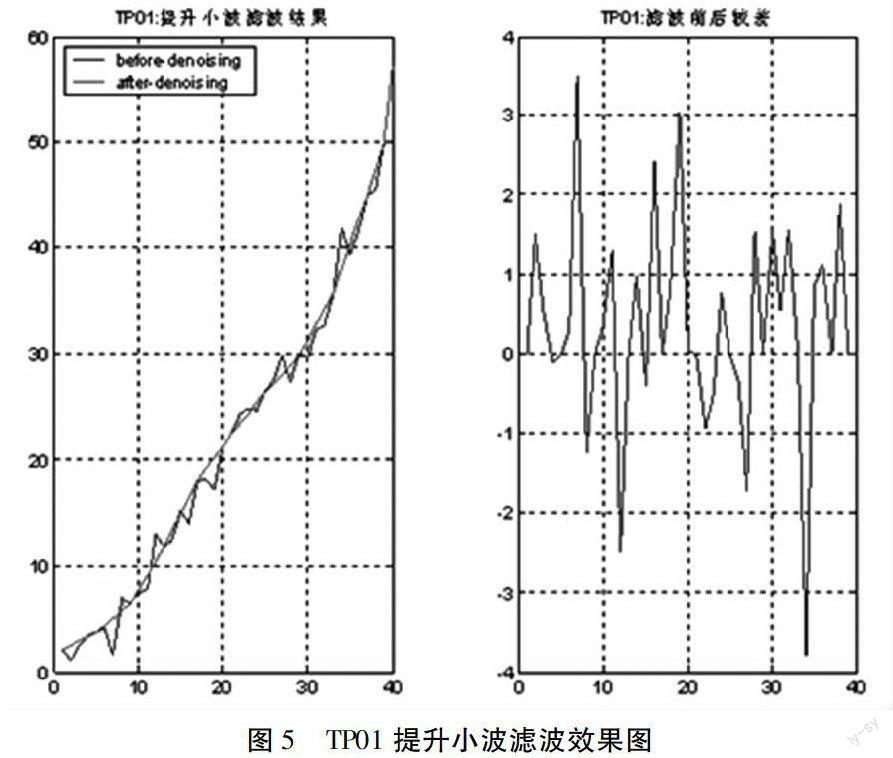
图5为采用提升小波对TP01的滤波结果。比较图4和图5，可以发现，提升小波具有和传统小波相同的滤波功能，且滤去的“噪声”更多，滤波后的曲线更为光滑。以监测精度σ=9mm为限差，即较差小于σ的即认为是“噪声”，由图5，TP01滤去的噪声均在±4mm以内，远小于监测精度，因此，可以认为滤去的都为“噪声”。

（2）应用二

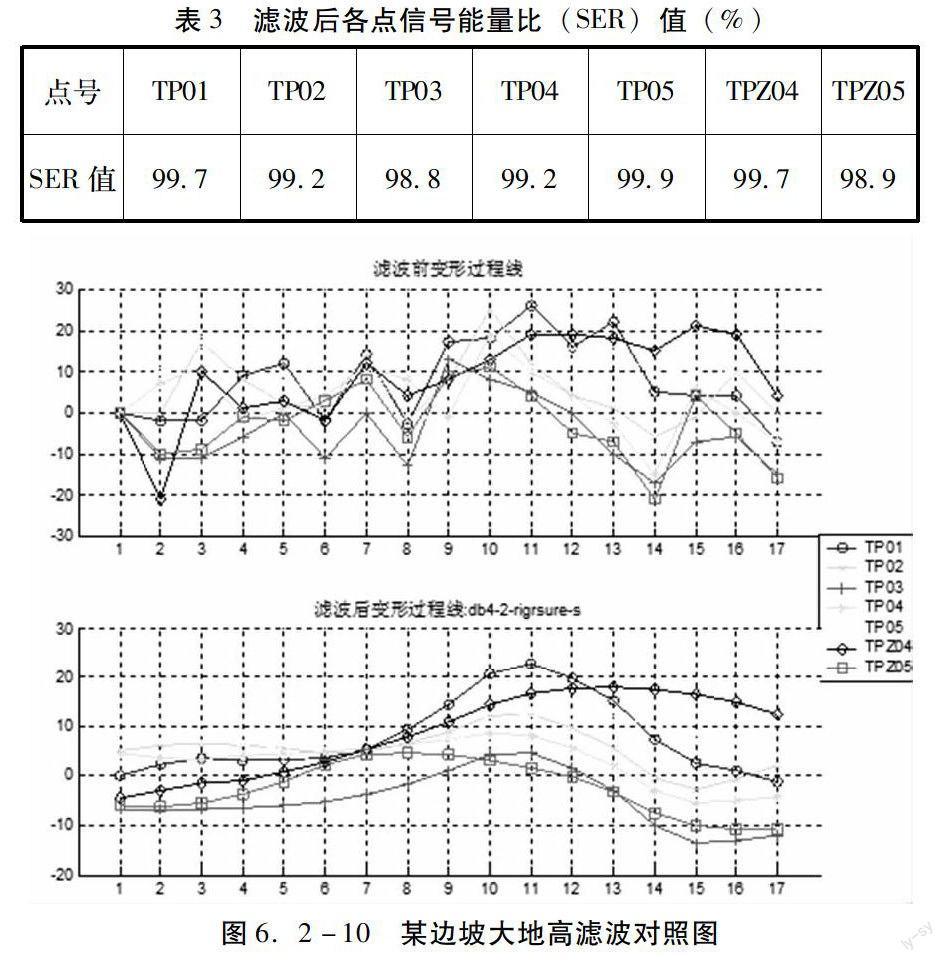
图6是针对某边坡大地高进行滤波生成的变形过程线对照图，表3为其对应的SER值。受测量环境、大地高测量精度等影响，大地高成果反映出的垂直位移过程线波动较大且趋势不明显；但滤波后的过程线不仅与原信号保持了较高的相似性（SER值均>95.0%），且直观地反映出各监测点的变形态势，即：各监测点大地高从首期观测至第7期复测无明显变化（垂直方向基本稳定），且累计变化值在±10mm范围内；第7期至第11次复测期间，各监测点大地高逐步增大（垂直方向缓慢抬升），最大抬升约17mm；第11期至第15期复测期间，各监测点大地高逐步减小（垂直方向逐步下沉）；第15期复测以后，各监测点大地高又基本无变化（垂直方向趋于稳定）。

根据上述分析，采用滤波方法对监测数据进行处理，获取的变形过程线不仅光滑性好，且保持了与原始过程线一致的趋势特征；利用滤波后的过程线，可以更直观、准确地判断监测点的变形态势（变形趋势、量级等信息）。

4.总结

受仪器精度、测量环境等影响，监测成果经常含有噪声甚至粗差，不利于进行变形态势评定或稳定性分析。采用滤波方法对监测数据进行去噪处理，可以获取“干净”的变形信息，以助于直观、准确判断变形态势，且可有助于建立准确的数学模型以进行深入的变形分析，如聚类分析、回归分析、变形预报等。

本文利用小波滤波对变形数据进行滤波处理，并采用能量比与噪声模（NM）以及光滑性与相似性等准则进行滤波效果的综合评价，得到了较好的效果，可为监测数据尤其是测量精度较低、测量环境复杂的监测数据分析提供参考。

参考文献：

[1]邓勇.滑坡变形分析与预报现代方法的研究.武汉大学博士学位论文，2008.6

[2]陈永奇等.变形监测分析与预报.北京：测绘出版社，1997

[3]吴子安.工程建筑物变形观测数据处理.北京：测绘出版社，1989

[4]黄声享，尹晖，蒋征.变形监测数据处理.武汉：武汉大学出版社，2004.7

[5]尹晖.变形分析与预报方法综述.东北测绘，2000.1