基于蚁群算法的智能交通最优路径研究

李松江，张异，龚跃

（长春理工大学计算机科学技术学院，长春 130022）

基于蚁群算法的智能交通最优路径研究

李松江，张异，龚跃

（长春理工大学计算机科学技术学院，长春 130022）

针对车辆智能交通最优路径问题，提出一种实时规划的蚁群算法。在该算法搜索过程中加入针对具体问题的局部搜索寻优算法，在启发函数中引入搜索方向，改进信息素更新策略，限制信息素轨迹量。利用智能交通道路模型对改进算法进行比较分析。实验结果表明，改进后的蚁群算法能够有效地解决车辆实时路径诱导问题，实现车辆实时路径诱导，具有良好的收敛性和寻优性。

蚁群算法；智能交通；最优路径

随着城市化进程的不断加快，道路运输需求的增加显著，城市机动车保有量的快速增长，使交通情况不断恶化，交通事故显著增加，人们在交通上消耗的时间和费用明显加大［1］。交通量的快速增长已导致了许多严重的社会问题和交通问题。为了减缓交通拥堵，提高道路的使用，节省交通消耗，使智能交通系统称为ITS（Intelligent Transport Systems），将网络信息系统、现代通信技术、智能化分析系统、定位系统等综合运用于整个道路管理系统的总称［2］。智能交通最优路径研究能够提供驾驶人员实时最优路径，在起点与终点之间根据实时道路信息，按照蚁群算法决策出最优路径。

1 基本蚁群算法

1.1 蚁群算法原理

意大利研究人员Dorigo M于20世纪90年代提出的蚁群算法（ant colony optimization，ACO），通过模拟蚂蚁的自然觅食行为提出的一种群集智能算法［1］。蚂蚁在经过的路径上会留下信息素，通过这条路线的其他蚂蚁可以感知信息素的多少，并选择信息素的多的路径。更多的蚂蚁选择信息素多的路径，形成一个正反馈机制。基于正反馈机制，蚂蚁可以找到从蚁巢到食物的最短路径。

1.2 蚁群算法基本模型

初始时刻，信息素τij(0)在各条路径上都是相等的。在算法搜索的过程中，蚂蚁决定下一步要选择的城市，根据城市间路径上信息素强度和城市间距离的大小［1］。t时刻时蚂蚁k从城市i到城市j的转换概率［2］：

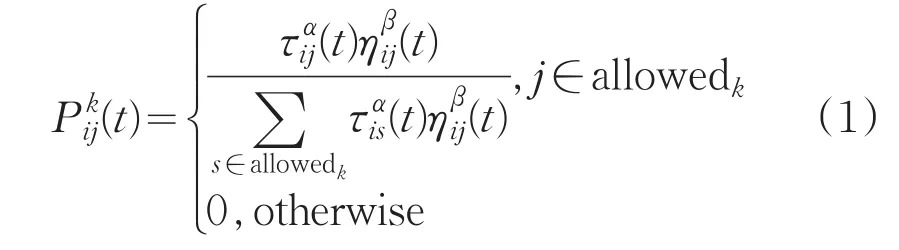
其中，allowedk={0,1，…，n-1}表示蚂蚁k下一步可以选择的城市。与转移概率成正比。α和β表示蚂蚁在搜索过程中启发信息多少和积累的信息素大小。

2 建立智能交通道路模型

单个交叉路口构成城市道路交通网络，用圆圈代表交叉道路路口，用直线代表路径，如图1所示。交通网络可以抽象成为由节点、弧段和路权组合成的有向带权图［3］。

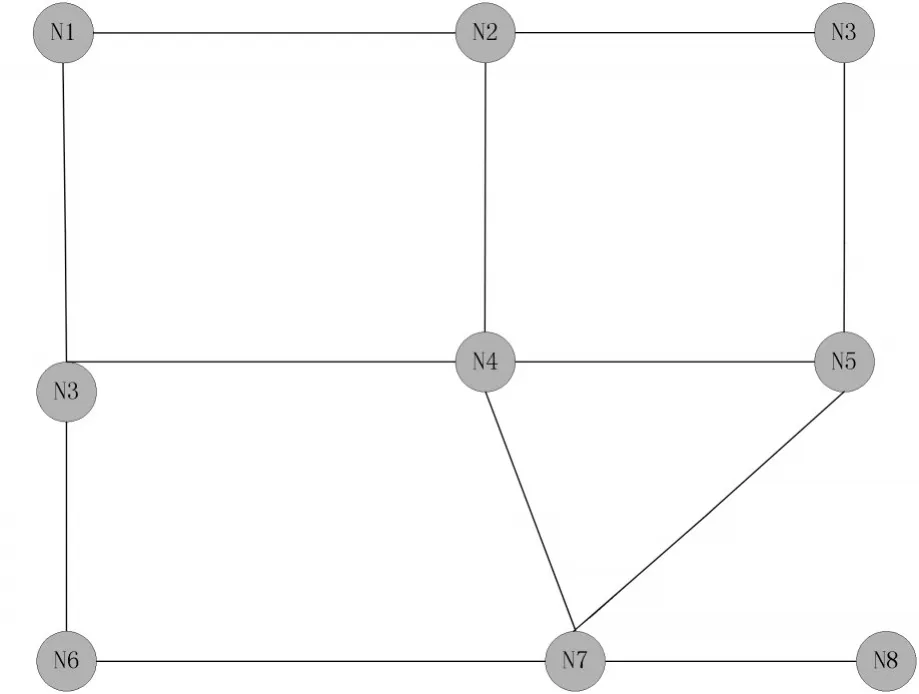
图1 道路网图论模型

G=(N,S,W)表示道路网络的状态图。G为有向图。N={Ni，i=1，2，...，8}表示交叉路口集合，S={Si=i=1，2，...，12}表示相邻交叉路口之间的路段，Wij={i,j|1,2,…,8}表示路段Ni到Nj的权重，是指通过Ni到Nj路段的所需代价值。

路段的权重由多个变量共同决定［3］。考虑该路段车流阻塞密度KS，路段通行能力MS和路段车辆排队长度PS,t这3个优化目标，则：

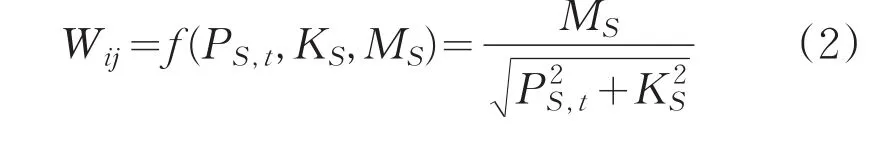
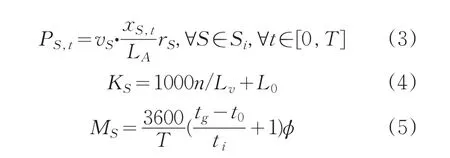
式（2）中：vS为路段S上车辆流密度，xS,t是路段S在t时刻的交通道路负荷，LS是路径S的长度，rS是路段S交叉路口红灯时长，T是红绿灯信号周期；式（3）中：n是路径S的车道数量，Lv为路径S阻塞情况下的平均车距［3］，Lo为路径S上平均车身长度；式（4）中：tg表示该交叉路口红绿灯信号周期，to表示绿灯亮时，通过停车线的车平均时间，ϕ是折扣系数，通常取0.9。

在实际生活中，传统算法决策出的最优路径并不能满足驾驶人员的实际要求［4］。传统最优路径中道路权值只和行车距离有关，是指车辆在起点和终点间选择一条距离最短的路径。最优路径定义为路径长度和时间费用综合最小的路径，并且在算法改进研究中将道路权值由单一距离改为由车流阻塞密度、车辆通行能力和车辆排队长度多个优化变量共同作用［7］。

3 改进的蚁群算法

3.1 期望启发式函数的改进

基本蚁群算法中，起点和终点连线方向的路径是最短的路径［8］。由两点之间直线最短可知。启发式因子t时刻在结点i和节点j之间距离的倒数表示：ηij(t)=1/dij。在导航路径问题中，算法期望蚂蚁选择向着终点方向的路径，所以改进后的期望启发函数：

其中，dqj表示起点到终点的距离。与基本蚁群算法相比，我们改善启发函数的搜索路径和方向的精度，并减少了搜索时间，并在搜索算法最后接近终点的过程中不断接近。

3.2 信息素更新策略的改进

最优-最差蚂蚁系统为了加大信息素在最优路径和最差路径之间的大小差别［9］。对蚂蚁构造出来的最优解进行增强，并且对最差解进行削弱［5］。更新最差路径上的信息素，当蚁群完成每一次循环构造出一条路径［10］。如果边（r，s）不是最优路径的边，是最差路径上的边，则这条边上的信息素更新公式如下：

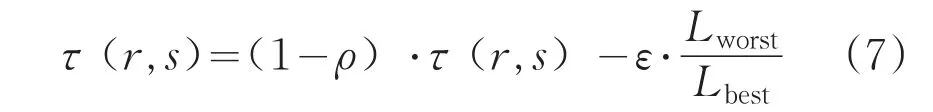
其中，引入参数ε，在［0，1］之间；Lworst是为最差路径长度；Lbest是最优路径长度；τ（r,s）表示城市r和城市s之间的信息素轨迹量大小［5］。

算法搜索集中在最优解附近，用来加快算法的收敛速度，减少时间和费用消耗。且在计算机运行算法的过程中，加减法运算要比除法运算节省很多时间［11］。在实际路径导航应用中，用户对时间的要求比其他因素要严格，为了提高算法计算准确性并加快计算速度，将除法运算改为加减法运算。信息素如下式所示：

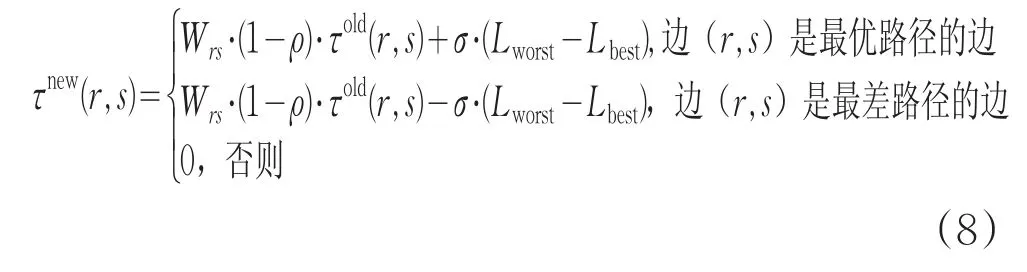
其中，引入参数σ，在［0，1］之间；Lworst是最差路径长度；Lbest是最优路径长度；τ（r,s）表示城市r和城市s之间的信息素轨迹量大小；Wrs表示边（r，s）权重［5］。

局部更新规则如下：

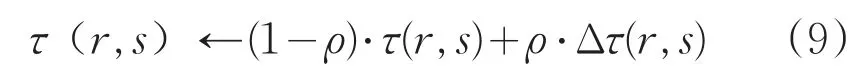
其中，ρ为一个参数，0＜ρ＜1。按以上公式进行一次更新每当蚁群完成一次循环构造出一条路径后。

3.3 信息素轨迹量限制

为了避免最优最差蚂蚁系统使信息素大小差异过大，出现算法停滞的现象。把信息素量范围限制在[τmin,τmax]区间内，以免信息素出现过大过小情况。限制信息素量的大小，可以提高算法性能，节省时间消耗，有效的解决算法停滞的情况。对所有的信息素轨迹τij(t)有：

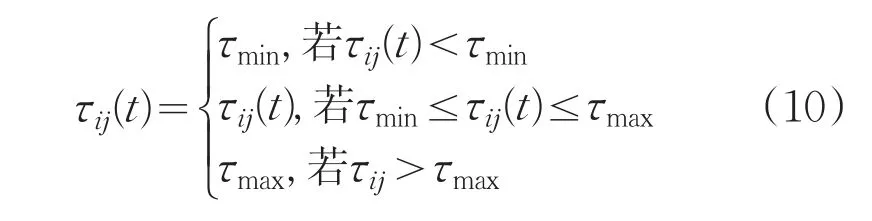
问题的关键是选择信息素轨迹界限。最大-最小蚂蚁系统收敛，表示的是在选择点上，一条路径上的信息素轨迹量是τmax，而其他所有可以选择的路径上的信息素轨迹量是τmin［5］。蚂蚁将一直选择信息素轨迹量最大的路径，直到最大最小蚂蚁系统收敛。

3.4 状态转移规则的改进

蚁群愿意选择路程较短而且存有很多信息素的路径作为下一步前进的路径。为了使状态转移规则有预见性，引入先验知识。先验知识是通过非感知理性获取的知识，它的基础不是感官世界，如：经验、概率知识，而是一种独立于经验的知识，选择路径公式如下：

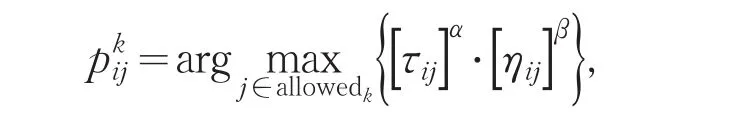
如果q≤q0按先验知识选择路径（11）

其中，0＜q＜1；0＜q0＜1。参数q0用来选择路径，决定是按状态转移规则还是按先验知识选择路径。随机选取参数q，在蚂蚁选择下一步行动路径之前。如果q大于q0根据式（1）状态选择规则选择路径，否则根据式（11）先验知识选择路径。

3.5 算法步骤

第一只蚂蚁依靠期望启发函数创建的第一条路径，而此条路径通常并不能正确的反应最优路径的大致位置。由于改进的蚁群算法是对最差路径上信息素进行削弱，对最优路径上信息素进行增强。所以在开始的几次搜索路径中，搜索到的最优路径中可能包含最差路径的边，而最差路径中包含最优路径的边。所以，如果在算法刚开始迭代时就增强所有最优路径上所有边的信息素，减少最差路径上所有边的信息素，整个蚁群算法将会陷入局部最优情况，影响智能交通最优路径算法的精确性和准确性。改进蚁群算法流程具体步骤：

（1）初始化。将m只蚂蚁放置于起点；所有路径的初始化信息素轨迹量为τij(0)；初始化循环次数Nc=0；初始化最大循环次数Ncmax。

（2）蚂蚁构造路径，每只蚂蚁依据表达式（11）选择下一个结点。

（3）应用局部更新规则。蚂蚁k完成一次循环路径构造，局部更新蚂蚁k构造的路径上一条边的信息素轨迹量。

（4）重复（2），（3）使所有蚂蚁都完成路径构造。

（5）全局更新最优路径上的边和最差路径上的边包含的信息素轨迹量和路径长度。

（6）禁忌表数据清空，把所有蚂蚁放置于起点。

（7）如果迭代次数小于Ncmax的1/4，重复步骤（2），（3），（4），（5），（6）。

（8）若果迭代次数大于或等于Ncmax的1/4，则按照式（8）对全局最差路径和最优路径上的路径信息素轨迹量进行更新。

（9）当循环次数满足Ncmax结束，否则跳转到（2）。

在蚁群算法开始搜索时并不进行路径信息素全局更新，减少时间消耗，运行代价消耗，加大算法的全局搜索范围。在经过若干次迭代后，算法能够确定最优路径的大致位置，再对路径上的信息素轨迹量进行更新，加快蚁群算法的收敛速度。

4 仿真实验

本次仿真实验使用MATLABV7.0，运行在Win7系统上。选择长春市吉林大路中段一段路网，构建路网模型。图2是选择的长春市吉林大路中段某一道路，用节点与节点之间的线段表示各道路，用节点表示交叉路口。将长春市吉林大路中段一段路网抽象如图3所示的网络拓扑图，设车辆在行驶过程中能接收实时路况信息调整规划路径。每条边上的交通属性由一个二元组（w，v）表示，表示边上的权重和平均车速。

车辆行驶起点为N1，终点为N18。设置参数NC=10，M=50，a=1，ρ=2，p=0.3，Q=1，W= 4，q0=0.1，NC=100，M=50；a=1，β=2，p=0.3，Q=1，W=4，q0=0.1；NC=200，M=50，a=1，β= 2，p=0.3，Q=1，W=4，q0=0.1。

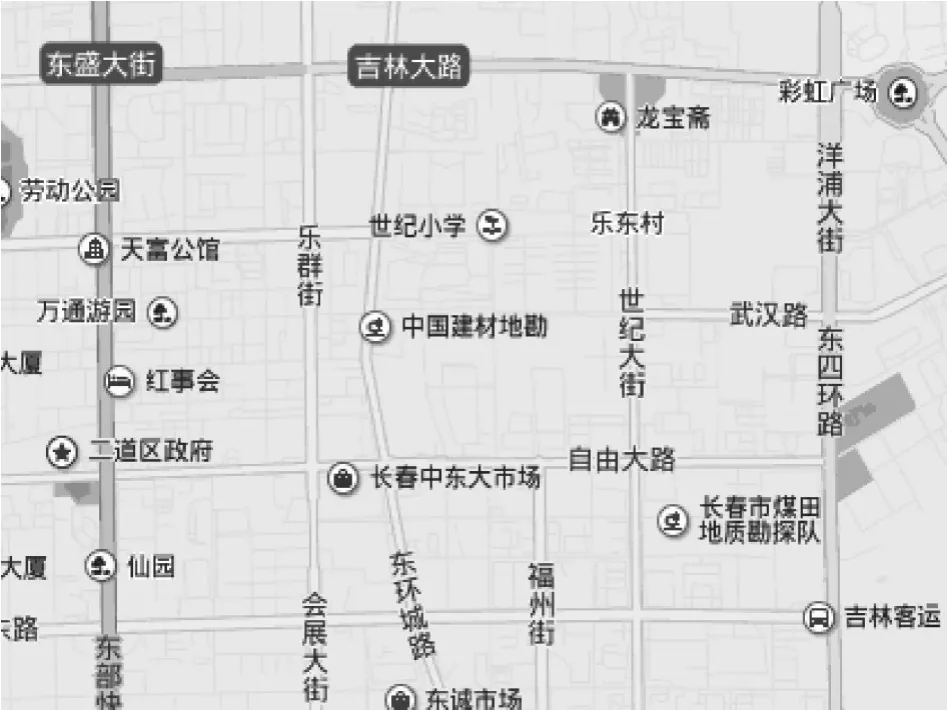
图2 长春市吉林大路中段道路

图3中路段状况实时变化用线段加粗表示，最优路径用加粗线段箭头表示。算法运行一段时间后找出初始当前最优路径，如图4所示。当车辆从N1行驶到交叉路口N5时，初始最优路径上N5到N10的密度及延时明显增大。此时算法进行局部更新。车辆选择N6继续前进。其他路径不变，有效的提高了效率。

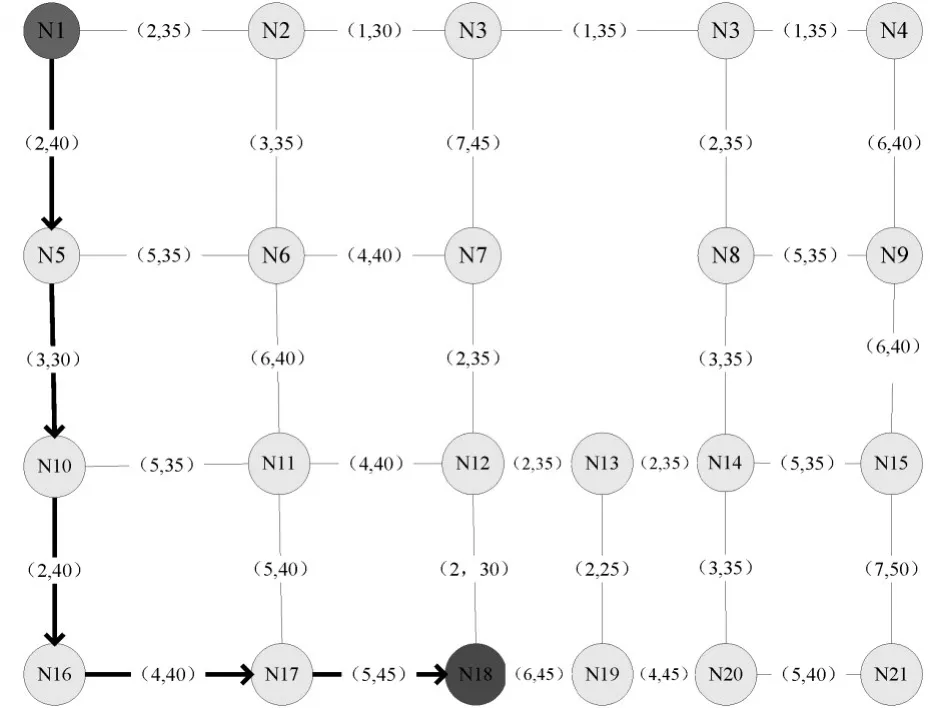
图3 网络格局图

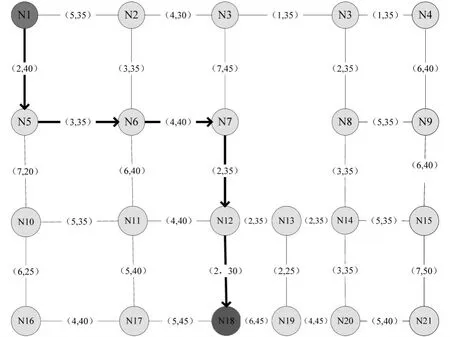
图4 重新规划网格格局图

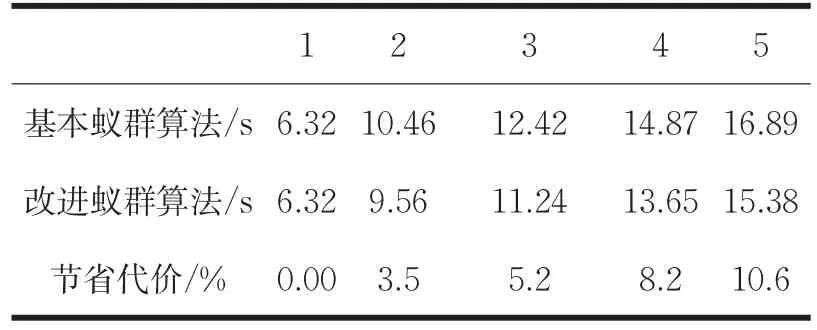
表1 两种算法的性能比较

实验结果表明，车辆最优行驶路径随着路段权重的变化在不断更新。以部分小型的道路路网作为实验场景，实时规划车辆调整行车路线。通过优化算法性能，尽可能减少行车耗时。改进蚁群算法针对收敛速度慢和容易陷入局部最优进行了性能方面的改进。减少算法时间上的浪费和增大运行的效率，能够有效的避免算法过早陷入局部最优情况。实验结果如表1所示：改进后的蚁群算法在实时动态调整最优解方面和在增加收敛速度、减少时间消耗方面，明显优于基本蚁群算法。

5 结论

本文建立了智能交通道路仿真模型，在状态转移规则中引入先验知识提高搜索效率。限制信息素轨迹量范围能够有效的避免算法出现停滞。改进信息素更新策略，加入道路权值因子，实现实时调整最优路径，减少时间和性能的消耗，加快蚁群搜索速度。实现车辆路径动态实时诱导根据实时信息变化，根据改进算法进行路径重规划。最后实验结果表明，该算法能有效地实时解决车辆在行驶过程中动态路径诱导问题。但是针对车辆在行驶中如何获取实时交通讯息及算法中参数如何更合理的搭配，还有待于进一步学习和研究。

［1］Dorigo M，Maniezzo V，Colorni A，Ant system：Optimizationbyacolonyofcooperatingagents［J］. IEEE Trans.on Systems，1996，26（1）：29-41.

［2］宋方，汪镭.改进的蚁群算法在智能交通中的应用［J］.数学的实践与认知，2013，43（3）：67-72.

［3］文孟飞，彭军，刘伟荣，等.一种增量式多目标优化的智能交通路径诱导方法［J］.湖南大学学报：自然科学版，2013，40（5）：56-60.

［4］Reimann M，Stummer M，Doerner K.A savings based ant system for the vehicle routing problem［J］.Proc.of the Genetic and Evolutionary Computation Conference，2012，32（12）：17-26.

［5］李士勇.蚁群算法及其应用［M］.哈尔滨：哈尔滨工业大学出版社，2004：82-89.

［6］吴启迪，汪镭.智能蚁群算法及应用［M］.上海：上海科技教育出版社，2004：56-60.

［7］Paola Pellegrini，Thomas Stutzle，Mauro Birattari.A study on max-min ant system for the TSP［J］.GermanyBerlinHeidelberg：Springer-Verlag，LNCS，2010（6234）：39-50.

［8］孙勇，李妮，龚光红，等.基于知识库的动态蚁群算法［J］.北京工业大学学报：自然科学版，2012，38（3）：74-80.

［9］Ugur A，Aydin D.An interactive simulation and analysis software for solving TSP using ant colony optimizationalgorithms［J］.AdvancedEngineering Software，2012，40（5）：341-349.

［10］赵飞，吴航，龚跃.蚁群算法解决网格环境下任务调度问题的研究［J］.长春理工大学学报：自然科学版，2013，36（2）：98-100.

［11］韩成，赵斌，白宝兴，等.基于集群的蚁群算法在TSP中的应用研究［J］.长春理工大学学报：自然科学版，2008，31（4）：110-112.

The Research on the Optimal Path of Intelligent Transportation Based on Ant Colony Algorithm

LI Songjiang，ZHANG Yi，GONG Yue
（School of Computer Science and Technology，Changchun University of Science and Technology，Changchun 130022）

Aiming at the intelligent traffic optimal path ant colony algorithm convergence speed is slow and easy to fall into local optimum problem proposed an improved ant colony algorithm，in the ant colony algorithm to search in the process of join to solve the concrete problems of local search optimization algorithm.In the heuristic function introduced search party to improved pheromone update strategy，limiting pheromone quantity，the state transfer rules introducing a priori knowledge，make ant colony tendency to have high adaptive value of search space，reduce the ant colony algorithm in blind search path into local optimum and shorten the search time.The experimental results show that the improved ant colony algorithm has good convergence and optimization，and can effectively avoid the stagnation of the algorithm in the local optimal solution，which proved the effectiveness of the improved algorithm.

ant colony algorithm；intelligent transportation；optimal path

TP391

A

1672-9870（2015）04-0122-05

2015-06-30

李松江（1984-），男，博士，讲师，E-mail：lsj84@outlook.com

龚跃（1960-），男，教授，博士生导师，E-mail：gongyue888878@sina.com