关于弧长概念的思考

2015-12-16彭娟范周田黄秋梅

教育教学论坛 2015年48期

彭娟　范周田　黄秋梅

摘要：在高等数学教材中，介绍弧微分定义是在给出曲线弧长定义之前，其中用到了曲线弧上两点非常接近时弧长与弦长之比极限为这一结论，由于学生很难理解，本文提出了两个解决方案。

关键词：弧长；弦长；第一个重要极限

中图分类号：G642.0 文献标志码：A 文章编号：1674-9324（2015）48-0244-02

度量问题是数学中一个非常古老的问题，而长度的度量是最常用的。有关长度的度量都以线段的长度定义为基础，例如计算平面上一段曲线的弧长，最早也是最直接的方法是用一些直线段来作出和曲线相似的形状，以直线段的长度代替曲线的弧长。仅凭直觉，关于曲线的弧长认识往往存在偏差，下面是一个典型的例子。

一、一个有趣的错误

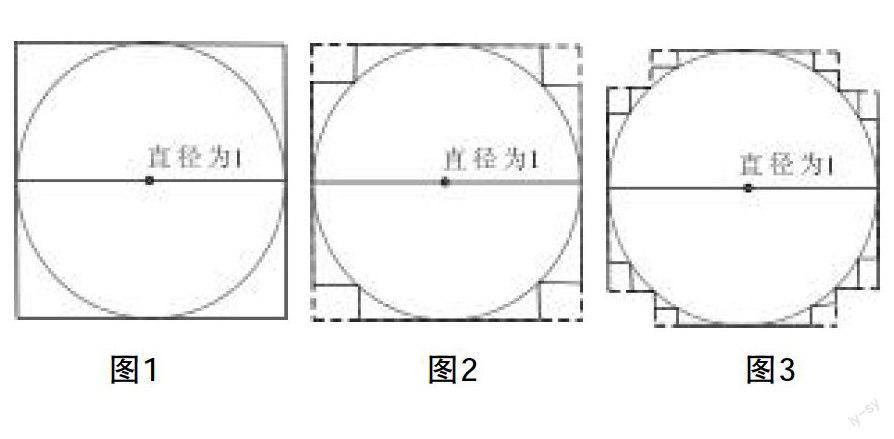
如图1，有一个直径为1的圆C，其长为L，在圆外作一个边长为1的外切正方形C1，其长为4；然后将正方形的四个角向内折，使得直角的顶点接触圆的边（见图2），这时曲线C2的长度仍为4；进一步将曲线C2的8个向外突出的直角内折，使直角的頂点接触圆的边（见图3），形成的曲线C3长度仍不变。同法，每次将曲线Cn-1的向外突出的直角内折，使其直角的顶点接触圆的边，得到曲线Cn，其长度一直不变。随着n的增大，曲线Cn越来越接近曲线C，所以曲线C的长度L=4，由此得到圆周率=圆周长/直径=4。

上面的做法隐含了这样一个假设：如果n趋于无穷时，曲线列Cn趋于曲线C，则曲线列Cn的长趋于曲线C的长。实际上，这个假设不成立。下面看一个反例。

二、有关弧微分和弧长定义的先后顺序问题

在多数《高等数学》教材的内容安排上，都是先讲授一元函数微分学，后讲积分学。为了介绍曲率都先给出弧长的微分的定义。

这里试图给出弧微分公式的推导，但其中用到的弧长与弦长之比趋于1这个暂时无法证明的结论，反而使得学生更难以理解，怎么解决大家的疑惑呢？有两种处理方法。

方法一：给个具体实例。

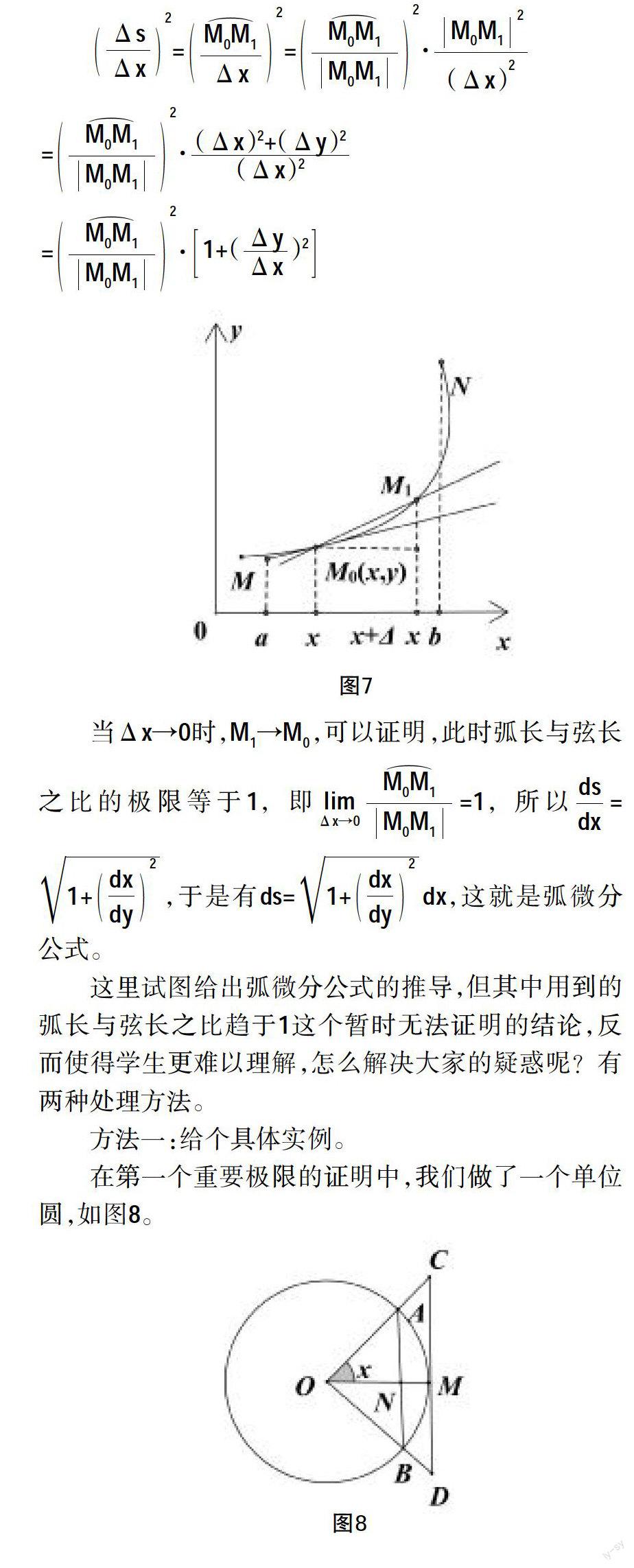
在第一个重要极限的证明中，我们做了一个单位圆，如图8。

由此我们得到了圆周上两点间距离很小时弧长与弦长之比极限等于1的结论，这是一个直观的例子，这有助于学生的理解。

教师在介绍第一个重要极限时，往往只强调这个极限在推导正弦函数导数公式中的作用，从未从几何上去分析它的实际意义，在教学过程中补充几何意义，即说明了圆周上距离很小的两点之间弧长与弦长之比极限等于1，这样会提升学生的学习兴趣。

方法二：先给出弧长的严格定义，再介绍弧微分。

弧长的定义默认了当曲线弧上两点无限接近时，弧长与对应弦长之比极限等于1，有了这个结论再介绍弧微分的定义就不会有什么困难了。

弧长的定义也说明了第一部分中求圆的周长应该利用圆内接正多边形的周长来逼近。

显然，从逻辑上来说方法二是一个最严谨的做法，但是现有的高数教材都是先介绍弧微分，后来在介绍定积分的应用时才引入弧长的定义。这是因为曲率属于导数知识的应用，讨论曲率必须有弧微分的定义；而弧长的计算属于定积分的应用，自然在后来才介绍。