静电场和静磁场的对称性和不变性分析
2015-12-16秦哲胡艳敏
秦哲 胡艳敏

摘要:在电磁学中,求解电荷或电流分布对应的静电场或者静磁场问题时,根据分布的对称性和不变性分析,总结静电场和静磁场的方向以及与空间变量的关系规律,同时将对称性和不变性分析贯穿整个包含有场分布的物理模型中,拓展学生的解题思路,也是对物理教学内容的补充。
关键词:对称性;不变性;静电场;静磁场
中图分类号:G642.0 文献标志码:A 文章编号:1674-9324(2015)48-0137-02
对称性和不变性是物理学的重要领域。物理学家不可能先验地知道我们这个世界涉及到的所有不变性和对称性,或已确定了不变性和对称性又不能完全确定物理量的形式。在电磁学中,对称性和不变性分析用于判断电磁场的方向以及确定电磁场与变量的关系,在分析解决具有一定对称性分布的电荷产生的电场或具有对称性分布的电流产生的磁场等物理问题时,引入物理定律或定理前如果能够初步判断各物理量的方向和空间变量的关系,可使问题的求解大大简化。目前国内大学物理教材,不论是在专业电磁学教材[1]还是普通物理教材[2]中,在利用高斯定理或者安环环路定理求解静电场或静磁场时,对电场或磁场的对称性和不变性分析较少,在得出结果时往往是默认物理量的对称性和不变性。比如在求点电荷的空间电场分布时,一般会利用高斯定理,选取合适的曲面积分,直接得出点电荷在空间电场强度的矢量表达式。对于场强方向的给出有些生硬,场强与空间变量关系的确定也是从结果的表达式来说明的,说服力不够。所以,在教学过程中,如果预先对点电荷分布的对称性和不变性进行分析和讲解,得出场强的方向和场强与空间变量的关系,再应用高斯定理得出场强的表达式,学生接受起来会更顺其自然。
笔者在长期从事中法合作办学机构,中国民航大学中欧航空工程师学院预科物理教学中,寻找中法物理教学的区别,探索符合中欧学院本科生普通物理学教学的方法,对国内物理教学也具有一定的参考价值。对于电磁学中静电场和静磁场的问题,法国物理教学过程注重电荷或电流分布的对称性和不变性分析,找出静电场和静磁场分布的规律。通过平移或旋转不变性研究场强与空间变量的关系;通过分析电荷或者电流分布的对称面和反对称面,找出对称面或反对称面上点的场强的方向,或者面外的一对对称点场强的对称关系。本文通过类比的方法总结了电荷和电流具有不变性和对称性分布情况下的静电场和静磁场。
一、静电场的不变性和对稱性分析
(一)静电场分布的不变性
如果带电体的电荷分布沿着某个方向具有平移不变性,电场强度即与此方向上的变量无关。例如无限大的带电平面周围的场强,沿着平面方向移动具有平移不变性,因此带点平面周围的电场强度就与这个方向的变量无关。如果带电体的电荷分布沿着某一个对称轴旋转具有旋转不变性,电场强度即与此旋转方向变量无关。例如一个无限长带电圆柱体,绕着中心轴旋转具有旋转不变性,因此周围的电场强度与旋转变量无关。另外,电场强度沿着中心轴的方向具有平移不变性,电场强度也与此方向的平移变量无关。如果建立坐标系,根据不变性可以判断电场强度与坐标系中具体某些空间变量的相关性。
(二)静电场分布的对称性
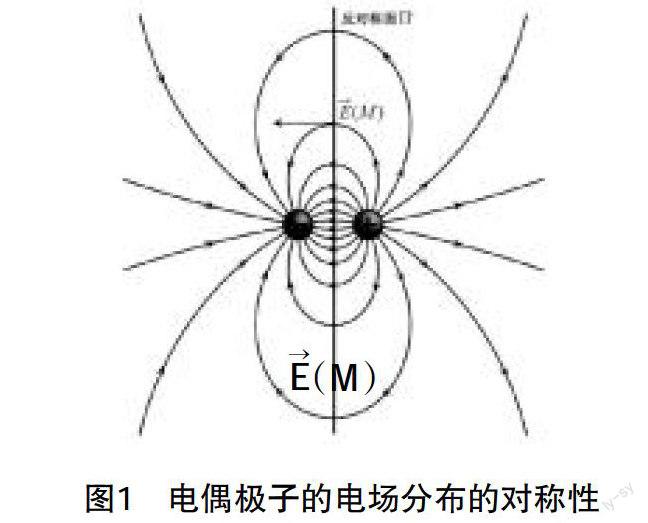
1.研究的点在对称面或者反对称面上。如果能找到电荷分布的对称面,记为Π,即电荷分布关于Π对称,在这个对称面上的点M的电场强度■(M)∈Π;如果能找到电荷分布的反对称面,记为Π′,即电荷分布关于Π′反对称,在这个反对称面上的点M的电场强度■(M)⊥Π′。例如两个距离为2a的一对正点电荷,垂直于两点连线且过连线中点的平面为此电荷分布的对称面,由此规律可以得知,对称面上的任何一点的电场强度的方向都平行于此对称面。如果是距离为2a的一对电荷,如图1所示,电量一正一负,那么垂直于两点连线且过连线中点的平面为此电荷分布的反对称面,反对称面上的任意一点的电场强度的方向都垂直于此对称面。
2.研究的点在对称面或者反对称面外。如果能找到电荷分布的对称面,记为Π,即电荷分布关于Π对称,在这个对称面外且关于对称的两点M和M′的电场强度和大小相等,方向关于Π镜面对称;如果能找电荷分布的反对称面,记为Π′,即电荷分布关于Π′反对称,在这个反对称面外且关于对称的两点M和M′的电场强度和大小相等,方向关于Π′反镜面对称。例如图2所示的电偶极子对应的电场分布,关于对称面对称的两点M和M′的电场强度和大小相等,方向关于镜面对称。
二、静磁场的不变性和对称性分析
对于静磁场的不变性和静电场的结论类似,对称性分析结论和静电场却刚好相反。
(一)静磁场分布的不变性
如果带电体的电流分布沿着某个方向具有平移不变性,磁场强度即与此方向上的变量无关。例如无限长的圆柱体导体模型通以一定电流,电流分布具有沿着圆柱体轴向移动具有平移不变性,因此圆柱体周围的磁场强度就与这个轴向变量无关。如果带电体的电流分布沿着某一个对称轴旋转具有旋转不变性,则磁场强度即与此旋转方向变量无关。同样是无限长的圆柱体导体模型通以一定电流,电流分布具有绕着中心轴旋转具有旋转不变性,因此周围的磁场强度与旋转变量无关。这类模型电流分布比较特殊,所以利用不变性很容易分析出磁场强度与变量之间的关系。如果电流的分布比较复杂的话,此结论不再适用。
(二)静磁场分布的对称性
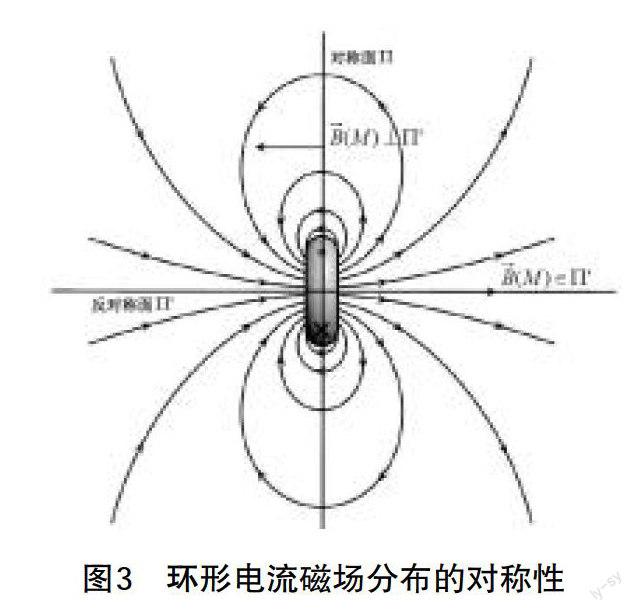
1.研究的点在对称面或者反对称面上。如果能找到电流分布的对称面,记为Π,即电流分布关于Π对称,在这个对称面上的点M的磁场强度■(M)⊥Π;如果能找到电流分布的反对称面,记为Π′,即电流分布关于Π′反对称,在这个反对称面上的点M的磁场强度■(M)∈Π′。如图3所示,一环形圆柱体导体模型通以一定电流,包含有此圆环的平面为此电流分布的对称面。由此规律得知,对称面上所有点的磁场强度的方向都垂直于此对称面。如果一个平面过圆环的中心轴,那么此平面为此电流分布的反对称面,反对称面上所有点的磁场强度的方向都平行于此对称面。
2.研究的点在对称面或者反对称面外。如果能找到电流分布的对称面,记为Π,即电流分布关于Π对称,在这个对称面外且关于对称的两点M和M′的磁场强度和大小相等,方向关于Π反镜面对称;如果能找到电流分布的反对称面,记为Π′,即电流分布关于Π′反对称,在这个反对称面外且关于对称的两点M和M′的磁场强度和大小相等,方向关于Π′镜面对称。
本文针对具有不变性和对称性分布的电荷或电流模型,分析和总结静电磁场的方向与空间变量之间的初步关系。对于分析电势和磁势的对称性、不变性以及静电场和静磁场的结论是相对应的。另外,在对本科生的教学中,不光是电磁场,凡是具有对称性和不变性的分布模型,都可使用对称性和不变性分析判断物理量的方向以及与空间变量的关系。在整个相关物理教学过程中,提高学生的物理素养,拓展学生的发散思维。
参考文献:
[1]赵凯华,陈熙谋.电磁学第三版(上)[M].北京:高等教育出版社,2011.
[2]程守洙,江之永.普通物理学第五版(2)[M].北京:高等教育出版社,1961.
