计及光照波动性及元件故障的光伏出力概率模型

龚娇龙 ,余志强

（1.国网宜春供电公司，江西 宜春 336000；2.南昌大学，江西 南昌 330031）

0 引言

随着化石能源的日益枯竭、环境问题的持续恶化，作为可再生能源之一的光伏发电因太阳能资源储备巨大及光电转换过程中的低污染甚至无污染的特点而备受社会关注。此外，光伏发电设备制造工艺的不断革新以及光伏并网技术的日臻完善，光伏发电正向规模化、集成化方向发展。光伏发电因受自然天气、地理位置因素影响导致其出力具有时序性和强随机性，大规模接入电网将给电网安全、稳定、可靠的运行带来极大的挑战。作为光伏发电基础的光伏出力建模就显得尤为重要。

文献[1]以光伏电池为基本单元进行了建模，其充分考虑了光照强度、光伏电池表面温度及光伏阵列遮挡情况对光伏电池出力的影响，但忽略了光伏电池出力的差异性和不同步性。文献[2]仅考虑了光照强度对光伏出力的影响，简单直接，但所建光伏出力模型精度上有所欠缺。文献[3]构建了光照强度遵循Beta分布的光伏发电随机出力模型，体现了光伏出力的随机性，但未考虑光伏面板表面温度对光伏出力的影响。文献[4-5]给出了采用最大功率点跟踪策略构建的光伏出力模型，并在此基础上，从不同角度研究了天气不确定性对光伏出力的影响，体现了光伏出力间歇性的特点。文献[6-7]分析了光照强度、光伏面板表面温度及光电转换效率对光伏出力的影响，并给出了光伏面板光电转换效率与光照强度的分段函数关系，整体提升了光伏出力建模的准确度。

上述文献从不同角度给出了光伏出力建模的方法，值得参考，但均未考虑元件故障对光伏出力的影响。鉴于此，本文提出了考虑光照波动性及元件故障的光伏出力概率模型，并将所建模型运用于算例分析，分析结果证实了所提出的光伏出力概率模型的准确性。

1 考虑光照波动性的光伏出力概率模型

就单座光伏电站而言，光伏阵列一般由同一型号的光伏面板组装而成，其输出功率与光照强度、光伏面板表面温度、光伏面板面积及光电转换效率有关，而光伏面板表面温度在短时间尺度上波动较小，其对光伏阵列输出功率的影响可忽略[3，6-8]。那么，由M块光伏面板组装而成的光伏阵列的输出功率为

式中：r为光照强度；Am、ηm分别为光伏面板面积和光电转换效率；M为光伏面板总数。

光照强度与电网负荷之间存在较强的相关性，为了削弱或消除这种相关性，通常将研究周期（如一周或一年）划分为多个时间间隔进行研究，时间间隔的长短由光照强度和电网负荷历史数据相关性统计分析决定。

在一定研究时间间隔内，光照强度近似呈Beta分布[8]，这是一种在区间[0，1]上的连续分布，其概率密度函数为：

式中：r、rmax分别为给定研究时间间隔内的实际光照强度和光照强度最大值，单位为W/m2；α、β为Beta分布的形状参数；Γ为Gamma函数。

Beta分布的形状参数α、β可通过给定研究时间间隔内r/rmax的期望值μ和方差δ计算得到[9]。

将式（1）代入式（2），可得光伏阵列输出功率的概率密度函数为

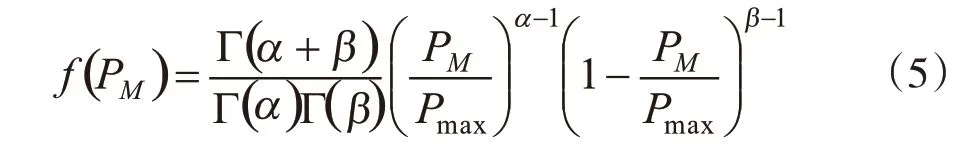
式中：Pmax、PM分别为光照强度为rmax和r时光伏阵列输出功率。令Pm为PM的离散形式，对应于区间[0，Pmax]均匀IM等分后的离散功率值，离散步长为δM=Pmax/IM，那么pm值的大小及其出现概率fm可用序对DM表示。

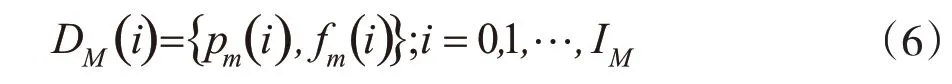
式中：pm（i）=iδM；pm（i）的出现概率fm（i）可通过式（5）在相应取值区间积分求得，公式为：

由式（7）可知，在给定功率离散状态数IM前提下，当光伏电站扩建时，只需对扩建后的离散功率水平pm（i）进行调整，而对应概率fm（i）保持不变。

2 光伏元件故障功率水平

热斑效应[10-11]是引起光伏元件故障停运的重要因素，其故障功率水平及对应概率序对DO可通过卷积定理[12]求解得到，则有：

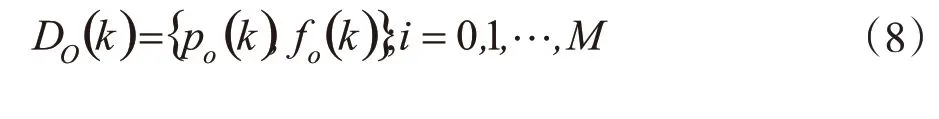
式中：po（k）=kPmax/M表示M块光伏元件中有k块光伏元件运行时的功率水平。

因光伏元件运行是彼此独立的，所以可通过二项分布或伯努力分布求出k块光伏元件正常运行时的概率，公式为

式中：qm为光伏面板不可用率。

对于由不同型号光伏元件组装而成的光伏阵列，其故障功率水平及对应概率值可通过递归算法[12]加以求解。

3 光伏出力概率模型

光伏出力概率模型的建立关键在于构建离散功率水平和对应概的序对DM与光伏元件故障功率水平和对应概率序对DO的联合概率分布。DM与DO包含的事件是彼此独立的，若离散功率水平i发生，则可利用式（7）计算出离散功率水平pm（i），若元件故障功率水平k同时也发生，那么光伏阵列的输出功率只有pm（i）的一部分，比例系数为po（k）/po（M）。当事件i-k发生时，光伏阵列的输出功率及对应概率可用如下公式表述。

事件i-k与事件k-i是两个互斥事件，但却有相等的功率值，即ps（i，k）=ps（k，i）=ikρs，因而其发生的概率可进行累加，令j=ik表示其联合状态。例如，事件j=8的概率等于事件（1，8）、（8，1）、（2，4）、（4，2）的概率之和。光伏出力概率模型的功率水平及对应概率可用公式表述如下。

式中：j=ik；i=0，1…，IM；k=0，1…，M。

4 算例分析

某2 MW 太阳能光电建筑应用示范工程由额定功率为200 W、面积为1.302 m2、光电转换效率为0.1537、不可用率为0.05的LDK 200 W 48-cell单晶硅光伏组件构成。为简化分析，将光伏组件分成40组，每组250块，其光电转换效率及不可用率仍为0.1537和0.05，PM的离散数IM的取值为4。图1给出了某光电示范站夏季典型日光照强度时序图，由图可知：夏季光照时间在上午6：00至下午19：00，各时段光照强度波动较大，光照强度最大值出现在中午13：00。

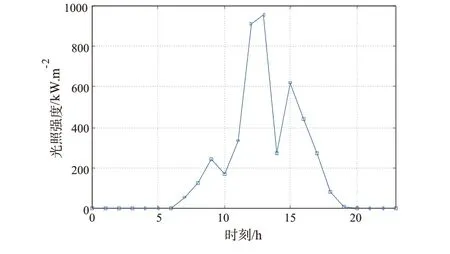
图1 某光电示范站夏季典型日光照强度时序图

图2给出了夏季典型日上午11：00时α=1.0166，β=0.5875的光伏出力概率密度分布和累积概率分布曲线，该图呈现出两端变化剧烈中间稳定特征。

图2 光伏出力的概率密度和累积概率分布

图3给出了该示范站夏季典型日光伏模拟出力与实测出力比较，由图3可知，光伏日出力曲线呈抛物线状，其出力时段基本在白天6：00-19：00，最大出力出现在12：00-14：00时段，幅值达装机容量90%左右，其他时段出力为0。仅考虑光照波动时，光伏出力与实测出力基本吻合，但在光照强度波动较大的中午时段，两者存在较大的误差，而考虑光照波动和元件故障的模拟出力降低了光照波动较大带来的误差，光伏电站模拟出力与实测出力曲线偏差程度为2.2%，说明所建光伏电站出力概率模型的可行性和准确性。

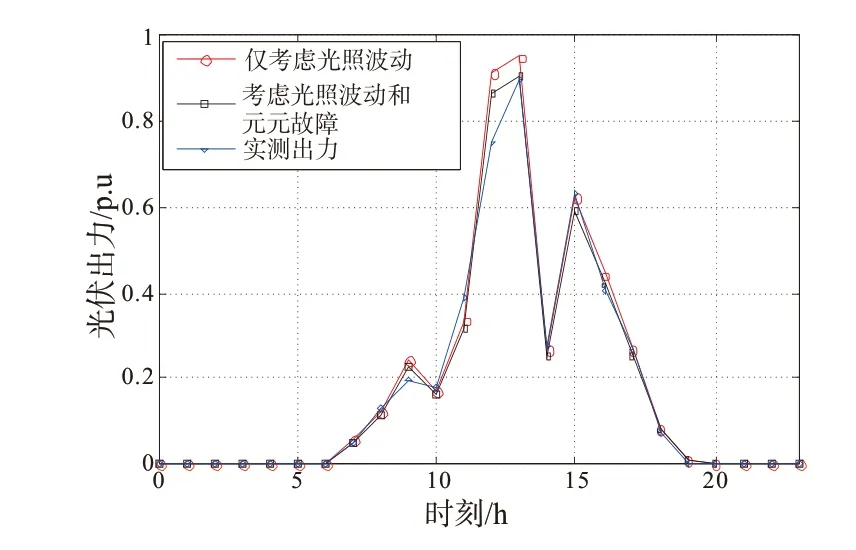
图3 夏季典型日光伏模拟出力与实测出力比较

5 结论

1）规模化、集成化是光伏发电的发展趋势，建立准确、可信的光伏出力模型不仅为电网的安全、可靠运行提供能量、容量价值，而且为光伏发电的置信容量评估的准确性提供了最基本的理论依据。本文提出的考虑光照波动性及元件故障的光伏出力概率模型，使得光伏出力得以细化，输出的功率值更接近光伏出力的实际值。

2）对于不同型号光伏面板构成的光伏阵列，同样可采用光伏出力概率模型以及运用递归算法进行光伏出力计算，说明了所建模型的适用性。

3）光伏并网主要考虑光照强度对光伏出力的影响，而忽略环境温度对光伏出力的影响。相比仅考虑光照波动性的光伏出力模型而言，本文构建的考虑光照波动性及元件故障的光伏出力概率模型更为准确，值得参考。

[1]柴亚盼，金新民，童亦斌.局部遮挡下光伏阵列的建模与仿真研究[J].电测与仪表，2013，50（12）：17-21.

[2]茆美琴，金鹏，张榴成，等.工业用光伏微网运行策略优化与经济性分析[J].电工技术学报，2014，29（2）：35-45.

[3]梁双，胡学浩，张东霞，等.基于随机模型的光伏发电置信容量评估方法[J].电力系统自动化，2012，36（13）：32-37.

[4]王秀丽，武泽辰，曲翀.光伏发电系统可靠性分析及其置信容量计算[J].中国电机工程学报，2014，34（1）：15-23.

[5]方鑫，郭强，张东霞，等.考虑天气不确定性的光伏电站置信容量评估[J].电力系统自动化，2012，36（10）：27-32.

[6]Cha S T，Jeon D H，Bae I S，et al.Reliability evaluation of distribution system connected Photovoltaic generation consid ering weather effects[C]//8th International Conference on Prob abilisticMethodsApplied to Power Systems.Iowa，US：Iowa State University，2004：451-456.

[7]王海瑛，白晓民，马纲.并网光伏电站的发电可靠性评估[J].电网技术，2012，36（10）：1-5.

[8]S.H.Karali，R.B.Chedid，R.Ramadan.Probabilistic Performance Assessment of Autonomous Solar-Wind Energy Conversion Systems[J].IEEE Trans on Energy Conversion，1999，14（3）：766-772.

[9]Abouzahr.I，Ramakumar.R.Loss of power supply probability of stand-alone photovoltaic systems:a closed form solution ap proach[J].IEEE Trans on Energy Conversion，1991，6（1）：1-11.

[10]Alonso M C，Ruiz J M，Chenlo F.Experimental study of mis match and shading effects in the I-V characteristic of a photo voltaic module[J].Solar Energy Materials&Solar Cells，2006，90（3）：329-340.

[11]邓夷.适用于复杂电路的IGBT 模型及大面积光伏阵列建模研究[D].北京：清华大学，2010.

[12]R.Billinton，R，Allan.Reliability Evaluation of Power Systems[M].PlenumNew，York，1984.