类土质滑坡稳定性影响因素及其相互作用规律研究

2015-12-16左昌群丁少林

水土保持研究 2015年3期

左昌群，徐颖，丁少林，唐霞

（1.中国地质大学工程学院，武汉430074；2.天津大学建工学院，天津300072）

目前，类土质边坡仍是一个较新的概念，国外尚无此概念，在国内也只有少部分学者进行了初步的研究，杨明［1］首次从研究花岗岩残积土边坡中提出类土质的概念，其特性主要表现其边坡的构成介质是经原岩风化后留在原地形成的残积物；赵晓彦［2］认为类土质边坡是由岩体风化而成，且具有原岩的结构面等特征，同时未经二次堆积，且稳定特性明显区别于均质土边坡及岩质边坡的一类边坡；唐亮［3］对类土质边坡的概念进行了进一步的完善，提出了类土质边坡也存在于沉积岩类风化层组成的边坡中。同时，也有许多学者对类土质边坡的性质进行研究，如张显坤［4］基于工程实例说明了传递系数法对类土质边坡的稳定性分析不适用；杨海平［5］采用改进的传递系数法对滑坡稳定性进行了分析；王浩［6］对类土质路堑高边坡的典型失稳机制进行数值模拟研究，系统归纳总结其变形失稳机制；陶宏亮［7］、万全［8］、陈天健［9］等分别探讨了库水位变化及降雨对边坡稳定性的影响；尤琳［10］、李明辉［11］等对复活型滑坡滑动机制进行了分析评价。但上述研究均未涉及类土质边坡的稳定性影响因素的敏感性分析，在此方面仍需进一步研究。

另外，许多学者对滑坡的敏感性分析也做了较多研究，如陈高峰等［12］基于均匀设计试验，研究了边坡稳定性的敏感因素；田东方等［13］采用正交试验法，对滑坡稳定性的影响因素进行了显著性检验；沈梦芬等［14］对膨胀土的水力学参数进行了边坡稳定性的敏感性分析，得出长时间的弱降雨对膨胀土边坡的稳定性有较大影响；张万涛［15］、葛华［16］等也对滑坡稳定性的影响因素进行敏感性分析，再次验证了正交试验在滑坡稳定性的敏感性分析中的有效性；在上述分析中，均未涉及对类土质滑坡的研究，且并未对主要敏感性因素之间相互影响机理进行进一步的深入研究。因此，本文对类土质滑坡稳定性影响因素的敏感性及其相互作用机理进行综合分析，以期掌握类土质滑坡稳定性影响因素的特点。

1 工程概况

永泰旗山滑坡丘顶平台标高227.0m，坡脚阶状住宅小区标高81.5～92.5m，相对高差145.5m，原始山体呈凸形，总体呈上缓下陡状，坡度20°～35°。滑坡处岩土体主要为素填土、残坡积黏性土、全风化凝灰岩、散体状强风化凝灰岩、碎裂状强风化片岩及中风化凝灰岩。另外，根据勘察资料可知，滑体及其周边出露的地层主要有侏罗系南园组及第四系更新统；同时，滑坡区范围内未发现大断裂构造通过，但滑坡区附近分布有局部区域构造。

2 滑坡稳定性因素的敏感性分析

2.1 评价指标及水平的选取

滑坡是地质体在复杂地质环境下的滑移变形破坏，其评价指标为其稳定性系数Fs。同时，根据滑坡稳定性的影响因素确定降雨强度、滑带土的抗剪指标、滑带土的重度和地表土的重度为影响因素的计算指标。

根据相关资料，滑带土内粘聚力的范围为20～26.1kPa，内摩擦角的范围为23.5°～26.6°，滑带土重度取值范围为16.5～25kN／m3，地表土的重度范围为18.2～25.7kN／m3。对于降雨强度的水平划分则采用控制总降雨量的方法进行确定。根据相关资料将总降雨量定为200mm，并依据降雨强度确定相应的降雨时间。根据上述各因素的取值范围，将各因素的水平定为5级水平，各因素水平划分见表1。

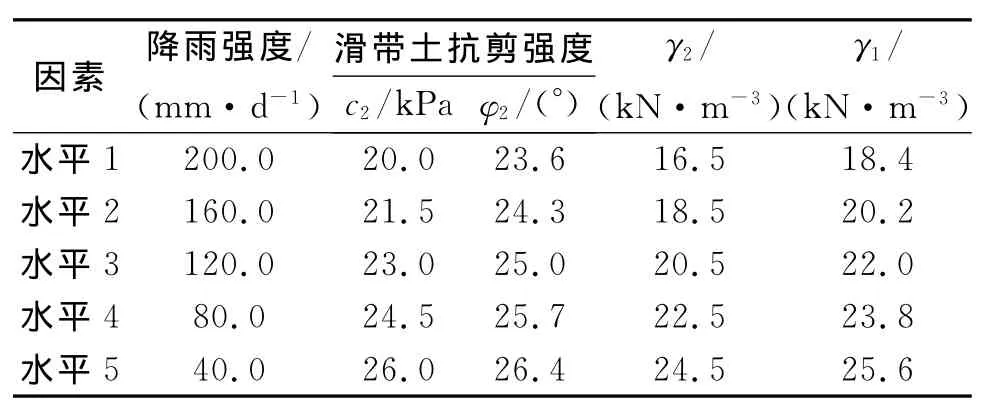
表1 各因素水平划分

首先采用seep／w模块模拟不同降雨水平对滑坡渗流影响，求得各降雨强度对应不同时步的孔隙水压力，再采用slope／w模块及Mogenstern－Price法对滑坡的稳定性进行模拟，得出各试验工况条件下的评价指标，即滑坡稳定性系数。

在模型的建立过程中，根据前期勘察资料，选取滑坡主剖面，建立永泰滑坡的力学模型，其下边界为竖向约束边界，左右边界为水平约束边界，地表部分为降雨边界。

2.2 正交试验方案设计与结果分析

（1）正交试验方案与计算结果。选取L25（56）正交表安排上述各因素正交的试验方案，并利用Geo－Studio软件对试验方案进行模拟，其计算结果详见表2。

（2）极差分析。根据上述试验结果，首先采用极差分析法对结果进行分析，极差分析结果见表3。滑带土内摩擦角对滑坡稳定性的极差值最大，且明显大于其他影响因子；其次，降雨强度、滑带土的粘聚力和地表土的重度，三者对滑坡稳定性的极差值相当，影响效果接近；最后，是滑带土重度的极差值最小。同时，根据计算得出最不利水平组合，求解出滑坡在最不利组合下，稳定性系数为0.901。

（3）方差分析。依据方差分析的原理，对试验结果进行方差分析，其F检验临界值见表4。根据前述方差分析方法，得出构造统计量，并将其与F检验临界值进行对比，得出各影响因素对滑坡稳定性的显著性程度并对其分级，方差分析结果详见表5。

降雨强度、滑带土抗剪强度指标和地表土土体容重的F值均大于显著性水平为0.01的临界值，所以上述4个影响因素对滑坡稳定性是高度显著性影响；滑带土容重的偏差平方和小于随机误差的偏差平方和，所以将滑带土的偏差平方和并入随机误差，不需要再对滑带土容重进行检验，滑带土容重对滑坡的稳定性无显著性影响。

同时，根据方差分析表对F值进行大小排序，同样得出滑带土内摩擦角的F值最大，且明显大于其他因素，其余排序也与采用极差方法对各因素的敏感性排序一致。因此说明极差分析与方差分析的结果具有一致性，可信度高。

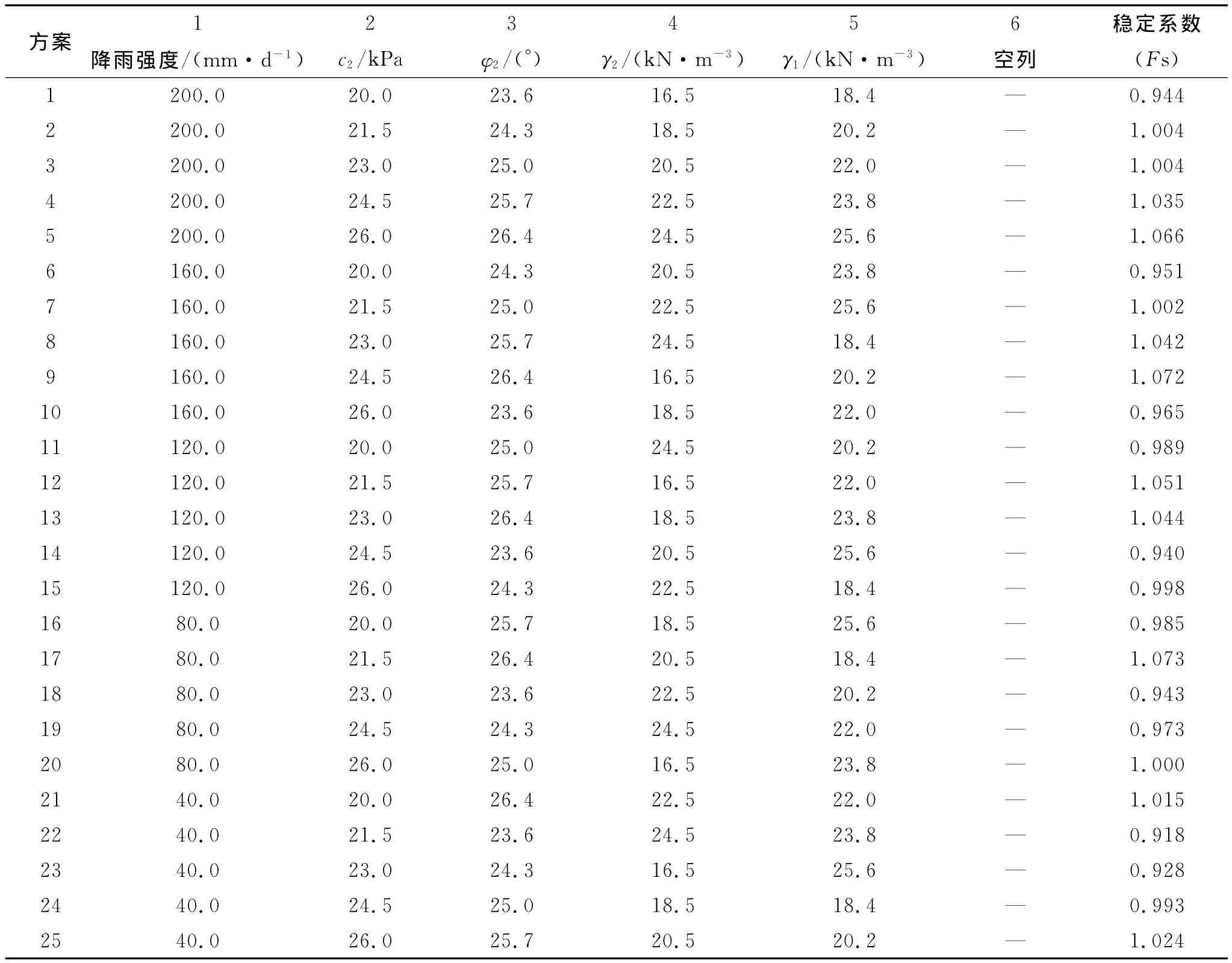
表2 正交试验计算结果

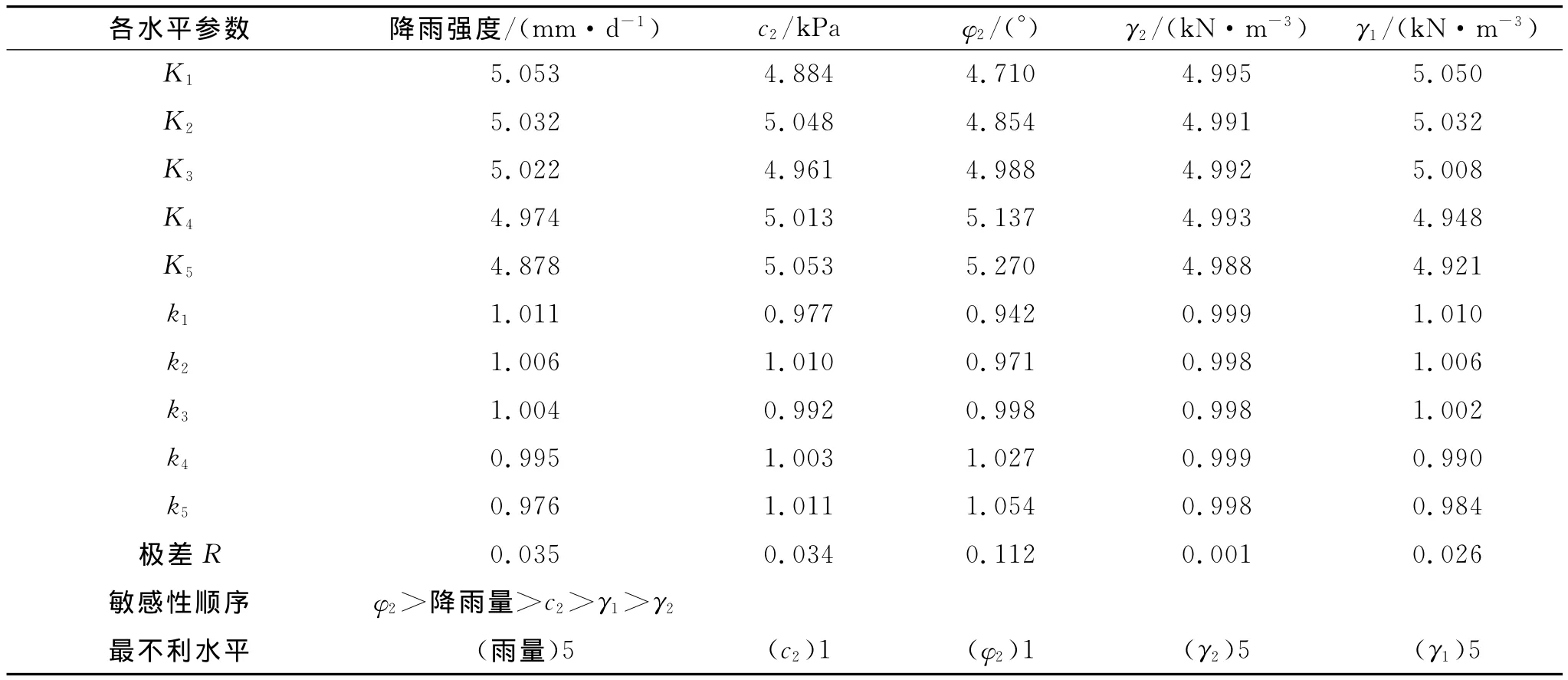
表3 评价指标极差分析

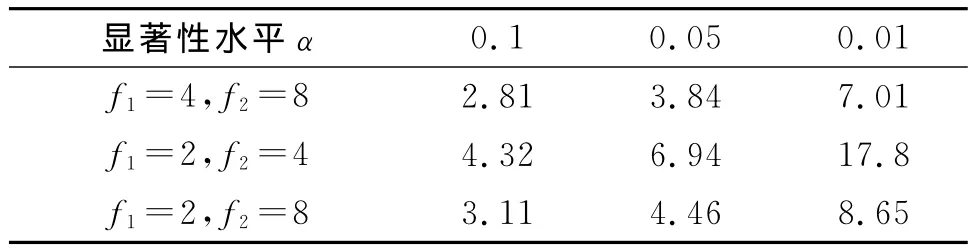
表4 F检验的临界值Fα（f1，f2）

2.3 考虑交互作用的显著性分析

另外，为了进一步了解各影响因素的综合作用对类土质滑坡稳定性的影响，再选取降雨强度、降雨历时和滑带土内摩擦角做交互作用分析。

根据交互作用试验的基本思想，采用L8（27）安排各试验，表头设计详见表6。滑带土内摩擦角的水平为24.5°，25.2°，降雨强度的水平为80，40mm／d，降雨历时的水平为3，5d。

对表6中的交互作用结果进行方差分析（表7），对滑坡稳定性影响最大的是滑带土的内摩擦角，其次是降雨历时、内摩擦角和降雨历时的交互作用、降雨强度、降雨强度和降雨历时的交互作用，最后是内摩擦角和降雨强度的交互作用。

表5 方差分析

表6 交互作用计算结果

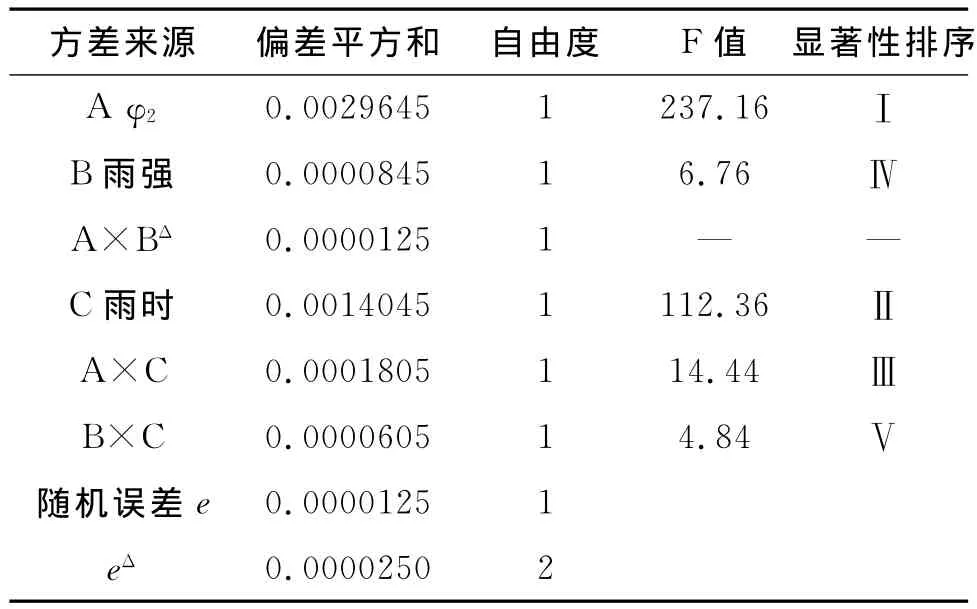
表7 交互作用方差分析

综上所述，滑坡不仅受若干单一因素的作用，还受它们之间交互作用的影响。在实际的工程防治中，要综合考虑各因素及其交互作用，提高滑坡防治的治理效果。

3 影响因素的作用规律研究

通过上述对滑坡稳定性影响因素的敏感性检验可知，降雨及滑坡土体的抗剪强度对滑坡的稳定性影响较大，但其相互作用规律仍需进一步研究，因此希望通过试验来进一步研究降雨与类土质滑坡土体抗剪强度之间的交互作用规律。根据勘察资料可知，滑坡所处地区主要以凝灰岩残积土、钾长花岗岩残积土和花岗闪长岩残积土为主。因此，本文试验选取上述3种土体为试验对象，并采用FDJ－20型四联式非饱和土直剪仪对3种类土质土样进行直剪试验；并且考虑到降雨对滑坡土体抗剪强度的影响主要表现为降雨改变滑坡土体的含水量，所以本试验主要研究含水量对不同类土质土体抗剪强度的影响。

3.1 试验说明

本次试验每组试样分别设计50，100，150，200 kPa四种不同的基质吸力状态，每种基质吸力状态下的剪切试验分别取100，200，300kPa三种不同的垂直压力状态进行。同时，本次试验固结稳定指标为每小时垂直位移变化量不超过0.005mm，固结过程可通过数据采集系统采集；另外，剪切阶段，在保持垂直压力和基质吸力不变的状态下，将水平剪切速率控制在0.148 0mm／min，开启剪切位移采集程序，本次剪切试验终止指标为两个条件：（1）若剪切位移在8mm范围内出现峰值，则峰值后2mm内可停止试验；（2）若8mm内未出现峰值，则剪切位移8mm处即停止试验，最大剪切力对应8mm处剪切力，试验后对土样进行开样记录。

3.2 试验结果分析

通过试验，得到相关结果，并根据经典莫尔－库伦强度准则拟合得出每种类土质试样含水量与抗剪强度的关系曲线，见图1，2。

（1）含水量对土体粘聚力的影响。含水量和粘聚力之间的回归方程如下：

凝灰岩残积土粘聚力随土样含水量变化分析的回归方程（拟合度0.94）：

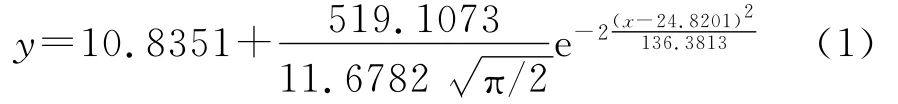
钾长花岗斑岩残积土粘聚力随土样含水量变化分析的回归方程（拟合度0.99）：

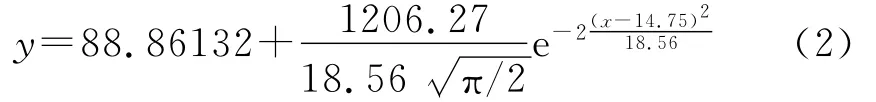
花岗闪长岩残积土粘聚力随土样含水量变化分析的回归方程（拟合度0.9）：

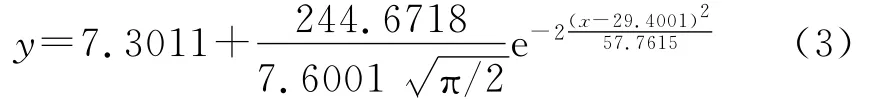
图1 各类类土质土样粘聚力随质量含水量变化曲线

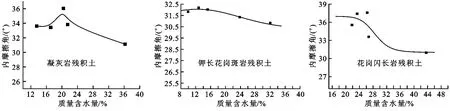
图2 各类类土质土样内摩擦角随质量含水量变化曲线

由图1可知，3种残积土粘聚力随含水量的变化趋势具有相似性，呈抛物线型，大致可分为两个阶段：① 土体的粘聚力随含水量的增加而增加；② 当含水量增加到某一程度时，土体的粘聚力随含水量的增加而减小。分析其主要原因是：从土体的微观角度分析可知，上述类土质土体含有黏土矿物，且黏土矿物主要为片状构造，其比表面积较大，具有很强的结合水吸附能力。当土体含水量较少时，土颗粒之间主要是以胶结作用连接，结合水作用较小。随着含水量的增加，使得土颗粒之间的胶结作用减小，而结合水不断增加，促使颗粒之间的相互作用力由胶结作用变为结合水作用，且结合水增加的作用力大于胶结作用减小的作用力，进而使得粘聚力增加。但随着含水量的进一步增加，使得土体结合水膜进一步增厚，反而降低了结合水的连接能力，土颗粒之间趋于游离状态，降低了土颗粒之间的相互作用，进而使得粘聚力出现下降。

但3种类土质的最优含水量不一致，凝灰岩残积土的最优含水量为24.82%，钾长花岗斑岩残积土的最优含水量为14.75%，花岗闪长岩残积土的最优含水量是29.4%，其原因主要是：3类残积土的矿物成分及微结构不一致。通过对3种土样的矿物成分分析可知，3种类土质黏土矿物总含量相近，但成分不同，花岗闪长岩残积土的黏土矿物成分主要为高岭石；凝灰岩残积土的黏土矿物主要为伊利石；钾长花岗斑岩残积土的黏土矿物成分主要为蒙脱石。蒙脱石的晶体是由很多相互平行的晶层构成，相邻两晶层间以负电荷的氧原子层相对，同性相斥，连结力极弱，有较强的活动性，进而晶层间可吸收不定量的水分子，而高岭石晶层间不对称相接，水分子不易进入晶层，伊利石则处于蒙脱石与高岭石之间，进而3类黏土矿物的亲水性排列顺序为：高岭石＜伊利石＜蒙脱石。从该角度上可看出含蒙脱石较多的土体，吸水能力更强，水分子易进入晶层浸润固体颗粒，进而使得颗粒之间的吸力增加（粘聚力），因此亲水性越强使得固体颗粒与水分子之间达到平衡所需要的水分子质量越小，即在较小的含水量的情况下，易达到自身粘聚力的最优含水量，该结论与试验结果有很好的一致性。因此3种类土质峰值粘聚力所对应含水量的不同是由自身黏土矿物成分及含量控制的。

（2）含水量对土体摩擦角的影响。对含水量和摩擦角的拟合回归方程如下：

凝灰岩残积土摩擦角随土样含水量变化分析的回归方程为：

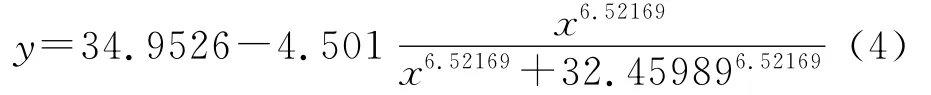
钾长花岗斑岩残积土摩擦角随土样含水量变化分析的回归方程为：

花岗闪长岩残积土摩擦角随土样含水量变化分析的回归方程为：

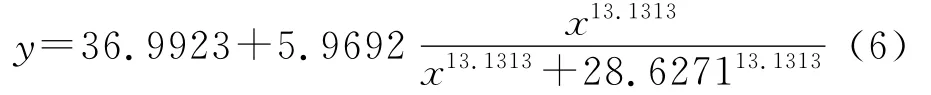
由图2可知，含水量对3种类土质试样摩擦角的影响具有很好的一致性，表现为随含水量的增加摩擦角不断减小，其主要原因仍可从微观角度进行分析：类土质土体在随含水量不断增加的过程中，结合水不断增加，使得土颗粒之间的孔隙不断增大，进而增加了孔隙内的游离水分子，该水分子对土颗粒之间的相对摩擦具有润滑作用，进而降低了土颗粒之间的摩擦角；另外，土颗粒外部包裹的结合水膜对土颗粒的运动也有润滑作用，是摩擦角减小的一个重要因素。

但含水量对3种土样摩擦角的影响程度不一样，表现为：含水量对花岗闪长岩残积土的影响程度最大，其次是凝灰岩残积土，最后是钾长花岗斑岩残积土。究其成因主要是3种类土质含有不同的矿物，进而使得其结构有所差异，对水的吸收能力也不一样，所以导致含水量对3种类土质摩擦角的影响程度不一样。

4 结论

（1）不考虑交互作用的正交分析结果表明：各影响因素对滑坡稳定性的影响不尽相同，其敏感性排序为滑带土内摩擦角、降雨强度、滑带土粘聚力、地表土的重度、滑带土重度。

（2）考虑交互作用的正交分析结果可知：对滑坡稳定性影响最大的是滑带土的内摩擦角，其次是降雨历时、内摩擦角和降雨历时的交互作用、降雨强度、降雨强度和降雨历时的交互作用，最后是内摩擦角和降雨强度的交互作用，说明各影响因素对滑坡稳定性的影响不是单独作用的，他们之间存在相互作用效应。

（3）含水量对类土质的抗剪性质具有显著的影响，其中粘聚力首先随含水量的增加而增加，当含水量增加到某一程度时，土体的粘聚力随含水量的增加而减小；同时，含水量对不同类土质内摩擦角的削弱程度不一样，其中对花岗闪长岩残积土的影响程度最大，其次是凝灰岩残积土，最后是钾长花岗岩残积土。造成上述现象的主要原因是不同土体微观结构和矿物成分组成之间的差异。

［1］杨明，王波，胡厚田.类土质边坡特征的初步探讨［J］.水土保持学报，2002，16（6）：110－112.

［2］赵晓彦.类土质边坡特性及其锚固设计理论研究［D］.成都：西南交通大学，2005.

［3］唐亮.类土质边坡稳定性分析与工程应用［D］.广州：华南理工大学，2010.

［4］张显坤.类土质边坡破坏的链式机理及对策跟踪［D］.重庆：重庆交通大学，2008.

［5］杨海平.基于改进的传递系数法滑坡稳定性分析［J］.水电能源科学，2013，31（5）：138－139，112.

［6］王浩.类土质路堑高边坡典型失稳机制与加固工程对策的数值模拟研究［D］.北京：铁道部科学研究院，2004.

［7］陶宏亮，范士凯，徐光黎，等.库水位变化条件下堆积体滑坡变形特征及稳定性分析［J］.水电能源科学，2014（5）：96－100.

［8］万全，范书龙，林炎.滑坡的多模型综合预测预报研究［J］.水土保持研究，2005，12（5）：185－189.

［9］陈天健，蔡和伦，黄彦荣，等.人工降雨模型试验研究降雨入渗对滑坡类型之影响［J］.水土保持研究，2012，19（1）：254－257.

［10］尤琳，沈军辉，彭昌翠，等.四川省青川县银溪窝滑坡复活机制研究及稳定性评价［J］.水土保持研究，2011，18（2）：44－47，52.

［11］李明辉，李浩然，王东辉.大渡河上游亚喀则滑坡复活变形机理及发展趋势分析［J］.水土保持研究，2014，21（1）：305－309

［12］陈高峰，程圣国，陈灯红，等.基于均匀设计的滑坡稳定性影响因素敏感性分析［J］.灾害与防治工程，2006，61（2）：38－42.