一个数学建模教学案例的分析讨论

□吴庆军，何家莉

（玉林师范学院 数学与信息科学学院，广西 玉林 537000）

一个数学建模教学案例的分析讨论

□吴庆军，何家莉

（玉林师范学院 数学与信息科学学院，广西 玉林 537000）

对一个数学建模教学案例分析讨论，从最简单的非线性规划开始，逐渐扩充约束条件，不断增加变量和约束条件，模型变成整数规划和0-1规划。达到了由一个案例展开得到建立各种数学规划模型的教学要求，对提高学生的综合素质能力有一定的指导意义.

数学建模；教学案例；创新精神

1 引言

数学建模教学过程中，要涉及到许多数学知识.文献[1-3]介绍了数学建模的优点，强调要分析建模的数学思维过程, 通过建模发生、发展、应用过程的揭示, 挖掘有价值的思维训练因素.文献[4]强调高校开展数学建模教学的意义与作用，介绍了数学建模教学与创新精神的培养以及数学建模教育改革的趋势.文献[5]叙述了以数学建模活动为载体开展数学建模教学的途径.在教学过程中需要精心设计教学案例，开展案例教学法，把好课后建模实践训练关,巩固和深化课堂教学，不断提高数学教师自身的水平来促进数学建模教学.

数学建模是应用数学知识解决实际问题的一门课程，需要应用多方面的知识.一个建模问题往往涵盖了数学不同学科的知识，这样学生学习这门课程有一定的难度，导致拿到一个实际问题往往无从下手.如果在教学过程中选择一个合适的案例把某一类数学知识集中系统的体现，让学生系统的学习某一类模型，是一个值得探讨的问题.本文结合多年建模教学经验，从许多经典的教学案例中抽出一个来做系统的分析讨论.

2 案例展开

货物供应中心的选址问题[6]

例1：某商业公司现有5家销售专卖网店，相应的分布位置坐标和每天的货物销售量如表2-1所示，该公司决定根据这5家专卖店的分布位置和销售量，选择一个合适的位置建造一个货物供应中心，负责向这5家销售专卖店运送货物.根据城市规划要求，货物供应中心只能建在以下四个顶点坐标分别为（8,10), (12,6),(18,6),(18,10)的四边形范围内，问题是在单位运费一定（不妨设为1元/km）的情况下，货物供应中心应建在何处才能使得每天的总运费最少？

表2 -1 销售专卖店的数据

我们开始提出这个实验案例时，先让学生思考，先提出经验方法，即指凭借个人或集体的经验做出决策.给学生介绍它的执行步骤一般为：(l)根据经验确定评价指标；(2)对各待选地点，利用评价指标进行优劣性检验；(3)根据检验结果进行决策.这种方法的优点是：注重历史经验，简单易行.其缺点是：容易犯经验主义和主观主义的错误,并且当可选地点较多时,不易做出理想的决策，导致决策的可靠性不高.

下面我们再提出如何采用定量分析方法.在建立一个选址模型之前,需要清楚以下几个问题：

（1）选址的对象是什么?

（2）选址的目标区域是怎样的?

（3）选址目标和成本函数是什么?

（4）有什么样的约束?

优化模型分为有约束和无约束模型.如果新建设施的地点没有限制,那么选址问题是无约束的选址问题.反之就是有约束优化问题.本题供货点被约束在一个四边形范围内，因此是有约束的选址问题.而根据实际情况的变化，可能会有多样的约束条件组成不同的模型.

针对本题，我们可将选址问题分为下面几类:

（1）非线性规划

我们建立一个供货站，坐标点设为(x,y)，假设供应给每个销售专卖店的运货量为ej.此题要实现的是总运费最少，那么目标函数f为运费.运费=运货量*距离*单位运费.单位运费是1，我们可以省略.对此先建立非线性规划模型，

根据题目要求，(xj,yj)要在已知的四边形D范围内.设计模型为

约束条件为：(x,y)∈D

x,y∈R

在用数学软件解决之前，先要把约束(x,y)∈D 变为实际的函数形式.

本模型用lingo9.0编程求解的结果为：x=8.4342，y=10，f=401.0859.

（2）整数规划

因为实际问题中，根据路况或者规划需求，当要求选址点必须是在整数位置时，此模型可以变成整数规划.

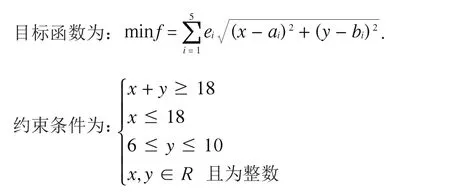
本模型用lingo9.0求解的结果为：x=8，y=10，f=401.4378.

这样此案例就可以拓展为整数规划模型.当然，我们也可以同时提出，如果只能在部分整数点上呢，这模型又该如何建立？

（3）0-1 规划

当供货中心可以任意选址时，我们建立起了非线性规划模型.但是，实际问题中不能任意选址的.有的只是数个可供选择的位置.那么如何在这有限的位置判断哪个位置的运费最省呢？突然发现原来的数学模型不适用了，需要在这基础上再做一个调整.这时候就可引入0-1规划.增加只能取0或者1的变量Yj，表示所在可供选择的位置上选取这个点为1，不选取这个点为0.(xj,yj)被约束在可供选择的D位置上.而模型其它的变量、函数、约束条件基本不变.假设有m个位置可选，这时候的模型就变成了0-1规划.

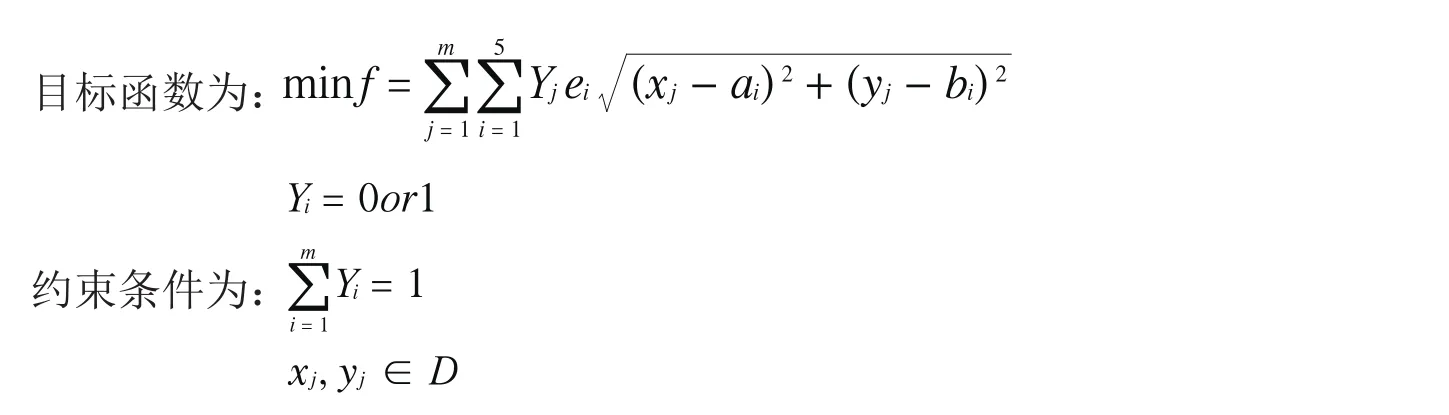
带入模型计算得出：Y1=1，Y2=0，Y3=0，f =434.3885，表明取(x1,y1)=(11,8)这个点作为供应点最优.

这三个数学模型分别从不同的约束条件解决实际问题.非线性规划模型约束最少，因此得到的结果最好 f =401.0859，其次是整数规划模型 f =401.4378，0-1规划可供选择的点最少，约束条件最多，因此费用最高 f =434.3885.

这样，通过一点一点深入探讨，能够把非线性规划，整数规划，0-1规划一系列数学规划模型都应用到此题中.让学生通过这个例题的学习，能够加深对数学规划模型的理解.当遇到其它类似的或者更为复杂的模型时，可以自主由浅入深地建立相应的规划模型，从而提高面对实际问题如何建立数学规划模型的能力.

3 效果分析

3.1 培养利用数学知识进行分析、推理、计算的能力

数学建模的每一个阶段都不能离开数学的分析、推理、计算.此案例正是给出实际问题，用数学建模的方式解答.在解答过程中每一个阶段都是由上一个阶段的推理、建模、计算得到.学生通过此案例的学习，能够分析问题，由简单的规划模型推演到复杂的更符合实际生活的模型.这就是一个通过自己分析，用数学推理抽象，描述实际问题的过程.最后通过不断的增加约束条件，建立相应的数学规划模型.

3.2 培养应用计算机、数学软件的能力.

随着计算机技术的迅猛发展，研究数学模型的手段也得到了飞速发展.要计算求解此题，必然要会熟练应用matlab或者lingo.而此题衍生出三个模型，让学生独立求解能起到很好的锻炼效果.通过自己编程，能迅速发现自己在软件方面的不足.通过计算出的结果，能反映出模型建立的准确程度，为模型的改进奠定了基础.

数学建模不仅需要学生具有对实际间题的洞察力、理解力、抽象能力以及运用数学语言建立数学模型的能力，而且还需要能够对所建立的数学模型进行算法设计、程序编制、上机计算及对计算结果进行科学分析的能力才能有效地解决实际间题.因此，在数学教学中大力加强数学建模教学，不仅可以极大地提高学生使用计算机的技能，而且可以进一步培养学生运用数学与计算机解决实际间题的能力.

3.3 培养和发展了学生的想象力、联想力、动手能力和创新能力

通过对此案例的教学研究，可以给学生提出几个问题探讨.

（1）如果没有直线道路，而只有几条既定弯曲的道路，该如何建模？

（2）目标函数仅仅是成本最省，如果增加一个时间最省的目标函数呢？因为每条道路的通行情况不同，节省费用但不一定节省时间.

（3）如果每天商店的需求量都在发生变化，则供货量该如何调整.

这能让学生充分发挥想象力、联想力和洞察力.不断提出新的问题，让学生自行想象，调查实际问题并解决问题，对学生的动手能力有极大的帮助.由此，需要学生对新产生的问题提出新的方法，新的模型求解.这样提高了学生的创新能力.

通过教学活动来培养学生的创新能力是眼下教育改革的重要主题.数学建模有助于学生更好地认识创新活动的过程.数学建模中经历“问题提出、问题分析、模型建立、模型求解、检验拓展”等创新思维的过程，可以使学生获得数学建模体验.

4 小结

本文选择了一个教学案例，并对其进行分析、讨论和拓展.根据题目先建立非线性规划模型，逐渐增加约束条件，模型逐步变成整数规划和0-1规划模型，然后用数学软件求解.

这教学过程培养了学生利用数学知识分析、推理、计算的能力，用计算机求解数学模型的能力，培养了学生的想象力、联想力、动手能力和创新能力.

本教学案例的展开分析充分发挥了学生的思考和想象空间，积极调动学生的学习兴趣.采用“启发式”和“实践式”教学，并在教学活动中恰当使用现代教育技术，理论与实践相结合，注重培养学生的创新能力，达到以点带面的教学效果. ■

[1]陈 莉，钟志华.数学模型方法的教育意义[J].牡丹江大学学报，2011，20(11)：132-144.

[2]徐龙封.在教学中培养学生数学建模思想[J].安徽工业大学学报：社会科学版, 2004，(3)：114-115.

[3]赫孝良，戴永红，周义仓.数学建模实验的探索[J].数学的实践与认识，2001, 31(5)：625-626.

[4]齐小刚，刘三阳.数学建模教育与创新精神培养的研究探索[J].实验技术与管理，2009，26(5)：27-29.

[5]王怀领.浅议高等数学建模教学策略[J].中国成人教育，2008(3)：154-155.

[6]韩中庚.实用运筹学[M].清华大学出版社，2007.

【责任编辑 谢文海】

Analysis and Study on an Mathematical Modeling teaching Case

WU Qing-jun HE Jia-li
(School of Mathematics and Information Science, Yulin Normal University, Yulin, Guangxi 537000)

A mathematical modeling teaching cases is analyzed and studied. The nonlinear programming is built first. With the gradual increase of variables and constraints, the model becomes the integer programming and 0-1 programming. The teaching requirement is met to establish various mathematical programming modeling through a case, and it has certain instructive meaning for the improvement of students’ overall quality.

mathematical modeling; teaching cases; innovative spirit

O29

A

1004-4671（2015）02-0016-04

2015-03-01

广西教育厅科学基金项目：201204LX335;2014区教育教学改革工程项目：2014JGA207。

吴庆军，男，广西玉林人，玉林师范学院数学与信息科学学院副教授，研究方向：最优化算法。