基于模糊理论的人体运动能耗监测

胡久龙瞿潮庆/.上海大学；.上海市计量测试技术研究院

基于模糊理论的人体运动能耗监测

胡久龙1瞿潮庆2/1.上海大学；2.上海市计量测试技术研究院

介绍了一种用于人体运动能耗监测的算法。这种算法是基于加速度频域分析和模糊理论的新算法，它使监测人体运动所需要的传感器数量更少且能稳定、可靠、准确地测量出人体运动的能量消耗。由于模糊理论的特性，这套算法更适应人体在自由运动状态下的各种运动形式，并具有很强的鲁棒性，因此可以更好地提供人体运动量监测信息以辅助解决由日常运动不足造成的肥胖问题。

嵌入式；三轴加速度计；模糊理论；运动量监测

0 引言

目前，身体肥胖问题令人担忧，肥胖带来的影响是多方面的，而首当其冲的是健康隐患。同时研究也证实，缺乏体力活动是导致慢性病发生的重要危险因素。而缺乏体力活动的一个重要评价指标是能量消耗的多少。有大量证据表明，经常参加体育运动对保持健康和预防慢性病有重要作用。因此，体力活动、能量消耗与人类健康之间存在着密不可分的联系。人体运动能耗的检测在很多领域都有重要的意义。在临床医学中，对有些疾病的治疗如甲亢就需要辅以科学的运动，这就需要一个针对性的运动方式和强度的指导方案，监测病人的运动能耗也变得必不可少。而在体育训练中，运动员也需要知道适合自己的最佳锻炼强度和锻炼时间，这样才能达到更好的训练效果。所以说，无论是健康饮食还是科学运动，都需要以能量消耗的监测为基础，没有这个基础，一切都无从谈起。因此，需要一个方便、可靠、易于实现的监测人体运动量的方法。

1 目标

人体的运动具有复杂的形态，且个体之间有较大的差异性，这就难以建立与之相对应的精确数学模型，也就难以实现对人体运动量的测量。目前常用的测量人体运动量的方法是以计步为基础，通过步频来计算人体运动量或者再辅助定位信息确定人体运动速度。这些方法的适用性非常有限，虽然能测量出较为平常的人体运动，例如跑步、骑行等，却难以有效应用于人体的其他运动形式。或者采用心率测量与加速度数据一起来测算人体的运动量[1]，通过将心率转换成新陈代谢速率辅助计算运动量的算法实现。这种方法的缺点有两个：一是心率的测量需要一个专门的传感器，一般有特殊的佩带要求，如戴在手腕等部位，不够简单易行；二是不同人群的新陈代谢速率与心率的关系有较大差别，例如运动员的心率比一般人要慢很多，这就会造成对不同人群的测量结果有较大差别。

本课题的研究目标是，实现一种仅对人体加速度进行监测就能有效反映出人体运动量的算法，而且这种算法要具有较强的鲁棒性。

2 算法设计原理

人体是一个复杂的运动系统，很难用传统的方法建立有效的模型与之对应。模糊理论在控制领域得到广泛应用并取得显著成效，适用于控制不易获得精确数学模型和数学模型不确定或多变的对象。很多问题无法用清晰的方法描述和解决，只能用模糊性方法处理。由于模糊逻辑本身提供了由专家构造语言信息、并将其转化为控制策略的一种体系理论方法，因而能够解决许多复杂、而无法建立精确数学模型系统的控制问题，所以它是处理推理系统和控制系统中不精确和不确定性的一种有效方法。

人在进行感觉、认知、推理和决策的过程中，往往都在运用和处理模糊概念。人脑有存储、处理模糊信息、模糊知识和进行模糊推理的能力，这正是人脑所具有的无与伦比的优越性。人能通过观察其他人的运动情况而得出相应的运动类型、运动强度等，这就是因为人具有运用模糊概念的能力[2]。同理可以把模糊理论运用到对人体的运动监测中：利用传感器记录人体的运动数据，将传感器数据与人体运动形态的对应关系按照模糊集的概念进行分类，并建立相应的模糊逻辑规则，然后通过大量的实验确定参数以及隶属度函数，最终确定相应的模糊系统。由此，模糊系统就可以较为准确地从传感器采集的数据得出人体的运动形态、运动强度等，进而计算出人体运动相应的能量消耗。

由于MEMS技术的进步和发展，微型三轴加速度传感器的准确度和稳定性已经达到相当水平，而且近年来用于检测人体运动能耗的许多研究中都采用三轴加速度传感器[3]，并能有效反映出人体的运动信息，所以本设计中也采用三轴加速度计作为测量人体运动的传感器，用搭载三轴加速度传感器微型嵌入式控制系统采集人体运动信息。此嵌入式控制系统可方便佩带在腰间，并配有数据存储模块，能连续不断地采集并记录人体加速度信息。

3 算法实现

此算法是以加速度信息为特征的、基于模糊理论的运动识别与能耗计算算法，算法中建立T-S型的模糊推理系统。首先对加速度信号进行频谱分析，得出有关人体运动的有效信息，然后根据这些信息确定模糊推理系统的参数，构建出具体的模糊系统，最后实验验证模糊系统的准确性。

3.1 加速度信号频域分析与处理

加速度传感器采集到的加速度信息中，包含了人体运动状态及运动强度等信息，也包含了其他噪声和干扰分量。通过对人体运动过程的分析得知：人在运动过程中的驱动力来自于身体各部分肌肉作用于各个关节的合力，而各个关节的运动状态是往复式的，所以人体运动的加速度在一定时间内是周期变化的信号[4]。因此，加速度信号中的有效部分应是周期变化的信号，傅立叶原理[5]表明：任何连续测量的时序或信号，都可以表示为不同频率的正弦波信号的无限叠加。为了滤除加速度传感器采集信息中与人体运动无关的信息，可以用频域分析的方法处理加速度数据，提取出最能反映人体运动特征的有效加速度信息。

对人体的运动分析可知，人体运动中最能指示人体运动信息的基础动作对人体最终的加速度贡献最大，即加速度信号频谱中幅值最大的频率分量即为表征人体运动的有效加速度信息。因此，对加速度传感器中采集的数据进行傅立叶变换，提取其中幅值最大的频率分量。频域处理后的加速度信息即可用来建立用于人体运动类型识别、人体运动能耗计算的模糊推理系统模型。

对加速度信号频域分析处理后得到的有效加速度信息为，人体运动加速度信号的有效频率分量的频率f及相应幅值a，它们既可以统计分析后得到与之对应的模糊子集（F集合），用于拟合模糊控制系统的隶属函数，构建模糊推理系统，又可作为模糊推理系统的输入量，以进行运动类型识别和运动能耗计算。

3.2 运动识别与能耗计算

T-S型模糊推理模型是由日本学者高木（Takagi）和杉野（Sugeno）提出的[1]，其目的是解决模糊控制理论中将模糊集合清晰化的过程过于烦琐、且结果具有很大随意性等问题，其输出是清晰值，或者输入量的函数，不需要经过清晰化过程就可以直接输出结果，更方便于数学分析。这个模糊推理模型不仅可以用于模糊控制器，还可以逼近任意非线性系统，适用于一般的模糊系统。加速度传感器所采集到的加速度信息和人体运动量之间的关系也是一个十分复杂的非线性关系，这里采用模糊推理模型对人体运动进行识别，然后针对不同的运动类型及强度级别来计算运动量。该模型不但解决了传感器信息到人体运动量之间的关系是非线性且过于复杂的问题，还解决了运动类型划分过细时不同运动间界限模糊的问题。

在本设计的模糊推理系统中拟建立7条模糊推理规则，以对应7种不同的人体运动状态类型。R1：静态（包括躺、坐、站立等状态），此状态下人体的能量消耗为基本的新陈代谢消耗；R2：慢走（如散步）；R3：走（较正常的步行状态）；R4：快走（较为匆忙的快步前行）；R5：慢跑（较悠闲的跑步状态）；R6：跑（步频、步幅适中）；R7：快跑（接近极限速度的跑步形态）。

同时，T-S型模糊推理系统的两个输入变量：频率f和幅值a也与所属的模糊子集合与模糊规则对应。将对应7种运动状态的F子集合定义为F1和A1、F2和A2、F3和A3、F4和A4、F5和A5、F6和A6、F7和A7。那么此系统中的7条规则为

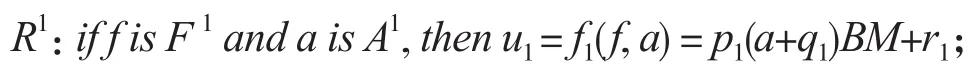
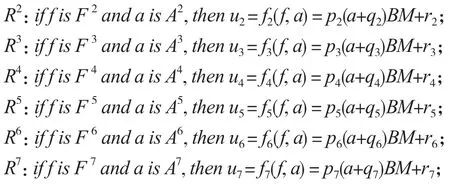
用Fi(f)和Ai(a)分别表示在第i条规则中，输入变量频率f和幅值a属于F集合Fi和Ai的隶属度。在人体的正常运动中，运动状态类型不变时，其加速度信号的有效特征信息也是不变的，可以认为它们满足均值为μ，方差为σ的正态分布N（μ, σ2）。因此，拟采用正态分布函数作为F集合Fi和Ai的隶属函数，即有：

通过实验，采集对应的满足各个规则时的加速度信号，并提取有效特征信息数据，然后可以确定用以拟合隶属函数的正态分布函数的参数μfi、σfi、μai、σai。至此，模糊推理系统已经建立，可以根据加速度信息进行人体运动状态识别。当T-S模糊推理系统的输入变量频率f和幅值a的值激活某一条模糊规则时，最终输出U的运动能耗的功率（kcals/min）将由这条规则的输出ui= fi（f, a）（即相应规则中的输出函数）决定。每一条规则所属的子集会与其他的规则所属子集有重叠的部分，但T-S模糊推理系统中可采用加权平均的方法解决这个问题。

本实验中选用乘积法计算权重：

最后，加权平均法计算总输出为

4 实验验证模糊推理系统的识别度

首先根据采样定理：为了不失真地恢复模拟信号，采样频率应该不小于模拟信号频谱中最高频率的2倍[6]，人体正常运动的周期高于0.1 s[7]，确定检测人体运动加速度传感器的采样频率为25 Hz。

4.1 建立人体运动状态的模糊推理系统

利用微型嵌入式数据采集平台，根据对人体运动识别和能耗推算的模糊系统模型的要求，对人体的7种运动状态采集加速度数据。然后，将这些采集到的数据上传到PC端进行频域分析，得出其中的有效频率和幅值。实验中，对加速度进行频谱分析时，除了发现频谱密度集中在有效频率附近外，还发现直流分量也有较高的幅值。分析得出，由于重力加速度和运动时空气阻力的存在，频谱中有较大的直流分量，因此将直流分量也作为表征人体运动状态的有效信息。模糊推理模型中的幅值信息输入有两项：直流分量和有效幅值。最终，建立模糊推理模型隶属函数的有效信息，即可表征人体运动状态的信息有三项：有效频率（除直流分量外幅值最大的频率）、有效幅值（与有效频率对应的幅值）和直流分量幅值。

根据前文假设的7条规则，实验采集加速度数据，频谱分析提取有效信息，构建模糊子集，最终建立模糊推理系统。按照算法的设计对每个子集进行正态分布拟合，各个子集中有效信息所属的正态分布的均值和方差如表1所示。

由表1中正态分布的参数可知，各个运动状态和相应的模糊子集有一定的对应关系。如果通过隶属度函数可以准确识别出所监测到的运动状态，则说明该模糊推理系统的准确性和强健性，说明该算法计算的人体运动能耗是可靠的。因此，实验验证隶属度函数的识别度，采集包含7种运动状态的人体运动加速度数据，代入识别度函数验证结果。

4.2 验证模糊推理系统的效果

为了验证模糊推理系统识别人体运动状态的情况，即模糊推理算法的效果，将实验采集的包含有各种运动状态的人体加速度数据，再进行频谱分析提取有效信息，进行状态识别。

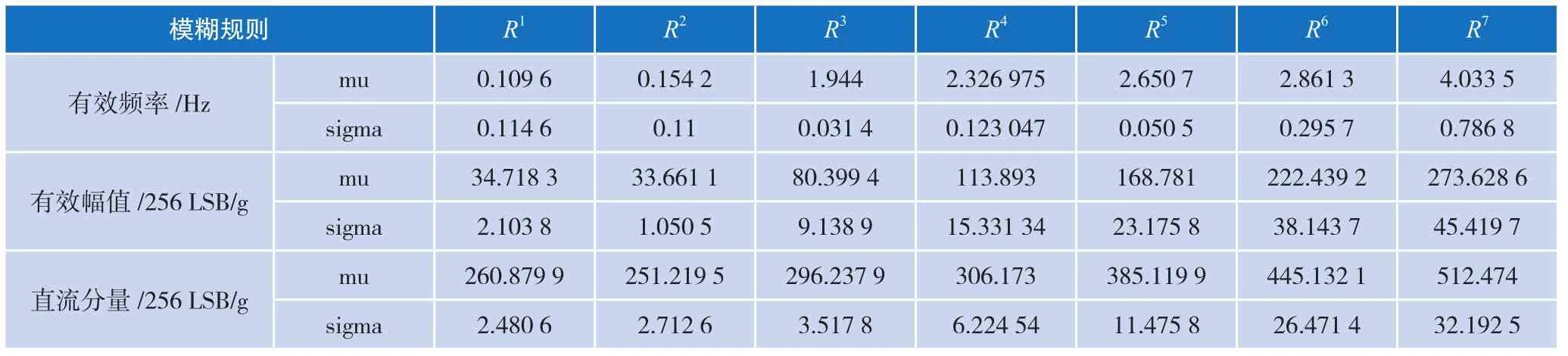
表1 运动状态正态分布表

首先，进行各个规则所对应的单个模糊子集的相应运动状态识别，如图1运动状态识别图中（a）（b）（c）所示。其中O形线表示相应的横轴所标示的模糊规则（R1、R2、…）所对应的正态分布隶属函数的均值，其他不同线宽的实线为实验所得的有效信息。

分别对比图1（a）（b）（c）中隶属函数的均值与实际实验所得的有效信息。图1（a）有效幅值验证识别图，对比有效幅值隶属函数的均值与实验所得实际运动的有效幅值信息，发现在规则R1、R2、R3实验条件下，实际情况与模糊推理系统有较高的一致性，且在规则R4、R5、R6、R7实验条件下相对于模糊推理系统隶属函数均值对称分布。图1（b）有效频率验证识别图，通过对比模糊推理系统的隶属函数均值和实验所得实际运动的有效频率信息，可知实验值与理想值有高度的一致性。图1（c）直流分量验证识别图，对比模糊推理系统的隶属函数均值和实验所得实际运动的直流分量信息，可知在规则R1、R2、R3、R4实验条件下，实际运动所得直流分量信息与模糊推理系统的隶属函数均值具有高度的一致性；在规则R5、R6实验条件下，实际运动所得直流分量信息虽然与模糊推理系统的隶属函数均值在对称性上略有偏差，却在集中性上有较好的效果；在规则R7实验条件下，实际运动所得直流分量信息相对于模糊推理系统的隶属函数均值对称分布。

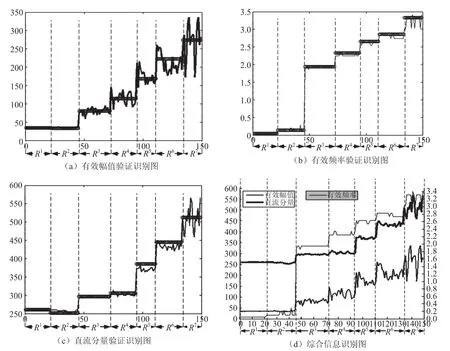
图1 运动状态识别图

然后，对各个规则上的对应三项有效信息的三个模糊子集综合起来的模糊推理系统进行运动状态识别。综合信息识别图如图1（d）所示，其中细、粗、中粗曲线分别为实验条件下对实际人体运动的加速度信息进行分析提出的有效频率信息、直流分量信息、有效幅值信息；横轴所标示的是与运动状态相对应的模糊规则。对比不同模糊规则对应运动状态下的三项有效信息，可知实际运动状态与模糊规则的对应有较高的唯一性。

通过单个模糊子集的识别效果验证结果得出，该模糊推理系统有较高的稳定性和一致性；通过综合三个模糊子集对每个模糊规则的识别情况的比较得出，该模糊推理系统对人体运动状态的识别有较高的唯一性。最终，可以确定该模糊推理系统可以准确识别出前文所划分的7种人体运动状态。由该模糊推理系统隶属函数对每一种运动状态的识别情况可知，基于T-S模型的模糊推理系统可以准确有效识别人体的运动状态，并具有稳定、可靠的特性；另外，由于模糊推理系统本身所固有的特点，该系统可以进一步细化运动状态的分类，可以更精细地识别到人体的运动状态。

5 结语

人体运动和人体加速度的关系复杂而多变，本文提出了基于人体加速度为输入、人体能耗大小为输出的T-S型模糊推理算法，将模糊理论用于人体运动能耗监测。目前多数对人体能耗的检测都是基于对人体运动步数及步速的算法计算的，这些方法在检测人体较为正常的运动情况时大部分时候是有效的，却因个体差异及人体的复杂性而会有较大误差。本文提出了先识别运动状态再进行能耗计算的方法。由于模糊理论的特点，基于模糊理论的人体能耗监测方法将是一种更有效、稳定、准确反映人体运动能耗与加速度关系的方法。实验也证实了这种方法的有效性和运动状态识别的准确性。由于实验条件及资金的欠缺，本设计并没有进行运动识别后能耗计算的实验。另外，基于模糊推理系统的特点，增加运动的分类即增加相应的模糊规则可提高模糊推理系统的准确度，得到更精确的运动状态分类与识别和进行能耗最终计算的准确性。由于构建模糊规则需要大量的实验数据分析，本文中未进行足够详细的运动状态分类划分及相关模糊规则的设计。今后可将模糊规则进行拓展细化，并对每条模糊规则的输出函数进行拟合与实验验证，使运动状态识别结果更准确可靠，使模糊推理人体运动能耗监测系统的适用性更强。

[1]Crouter S E.Accuracy of the Actiheart for the assessment of energy expenditure in adults[J].Eur J Clin Nutr,2008 (6)∶704-711.

[2]黄军辉,傅沈文.模糊控制理论的发展及应用[J].中国科技信息，2006（12）：303-304.

[3]朱国忠，韦彩虹，潘敏.基于三维加速度传感器的人体运动能耗检测算法的研究[J].传感器技术学报，2011（08）：1217-1222.

[4]王险峰，洪炳镕，朴松昊，等.一种仿人机器人跑步状态分析模型[J].计算机研究与发展，2011，48(9)：1740-1747.

[5]Steven W，Smith.The Scientist and Engineer's Guide to Digital Signal Processing[M]．California ： California Technical Publishing，1997.

[6]石辛民，郝整清.模糊控制及其MATLAB仿真[M].北京：清华大学出版社，2008.

[7]张卫强, 陶然. 分数阶傅里叶变换域上带通信号的采样定理[J].电子学报，2005(07)∶45-48.

[8]Antonsson E K, Mann R W.Mann R W. The frequency content of gait[J]. J. Biomech. ,1985（18）：39-47.

Monitoring of human movement energy consumption based on fuzzy theory

Hu Jiulong1Qu Chaoqing2
（1. Shanghai University, 2. Shanghai Insititute of Measurement and Testing Technology）

This paper describes an algorithm for monitoring of human movement energy consumption. This algorithm is based on the acceleration frequency domain analysis and fuzzy theory. It needs less sensors to monitor human movement and the measurement of energy consumption is stable, reliable, and accurate. Because of the characteristics of fuzzy theory, this algorithm can adapt to various forms of human exercise in the free state of motion, and has strong robustness. It can provide more monitoring information to solve the obesity problem as an auxiliary solution caused by insufficient exercise routine.

embedded; triaxial accelerometer; fuzzy theory; exercise monitoring