城市公交网络拓扑特性与鲁棒性实证研究

张琳，傅白白，殷增超

（1.山东建筑大学 交通工程学院，山东 济南 250101；2.山东建筑大学 建筑城规学院，山东 济南 250101）

城市公交网络拓扑特性与鲁棒性实证研究

张琳1，傅白白2*，殷增超2

（1.山东建筑大学 交通工程学院，山东 济南 250101；2.山东建筑大学 建筑城规学院，山东 济南 250101）

公交网络拓扑特性与鲁棒性是评价城市公交网络可靠性的两个重要方面。文章选取截止到2014年5月的济南市195条公交线路和1433个站点为样本数据，采用 space L方法构建济南市公交地理空间网络模型，分析公交网络站点度及度分布、平均最短距离、平均聚类系数、介数、网络有效性、网络最大连通率等拓扑性质；对济南市公交网络鲁棒性进行实证分析，并给出优化对策。结果表明：济南市公交网络具有较小的平均最短距离和较大的聚类系数，度分布为指数 λ=2.112的幂律分布，是具有小世界特征的无标度网络；该网络对随机攻击具有鲁棒性，对蓄意攻击具有脆弱性，基于度数的蓄意攻击对公交网络鲁棒性影响最大。

复杂公交网络；space L方法；拓扑性质；鲁棒性；优化对策

0 引言

城市交通系统是一个复杂巨系统，具有时空复杂性。随着复杂网络小世界效应和无标度特性的提出，为广大交通领域学者提供了一种全新的研究视角［1-2］。相关文献表明，铁路、高速公路、航空、公交等交通网络都具有无标度或小世界特性［3-6］。近年来，公交网络拓扑特性分析与鲁棒性优化对策已经成为复杂交通网络研究的热点。Wu等以网络局部有效性为度量，分析北京市公交网络在随机攻击和蓄意攻击下的鲁棒性［7］。Ferber和Berche等从世界范围内选取14个城市的公交网络，以网络连通性和平均最短路径长度为度量，研究网络应对随机攻击和蓄意攻击后的恢复能力，得到不同城市的公交网络面对攻击时具有多样化的行为特征［8，9］。汪涛等选取国内四个城市公共交通系统为研究对象，以网络最大连通子图相对大小和效率为度量研究公交网络的抗毁性［10］。王波等基于三种方法对杭州市公交网络建模，分析公交网络拓扑特性，得到杭州市公交网络是具有指数型度分布、明显社团结构和较强传播能力的小世界网络［11］。郑啸等通过构建基于邻接站点的有向加权复杂网络模型分析北京市公交网络的拓扑性质，并给出基于承载压力分析和“掠夺”的两种区域中心节点提取方法［12］。

公交网络在城市综合交通运输系统中发挥着重要的作用，研究公交网络对城市综合交通运输系统具有重要的现实意义。公交网络作为济南市公共交通的主要构成方式，其站点数量、线路设置、日均流量等均具有典型代表性。文章以济南公交网络为例，采用space L方法构建济南市公交地理空间网络模型，分析站点的拓扑参数；基于公交网络鲁棒性仿真实验，对济南市公交网络鲁棒性进行实证分析，并给出公交网络鲁棒性的优化对策。

1 复杂网络典型拓扑结构

具有自组织、自相似、吸引子、小世界、无标度中部分或全部性质的网络称为复杂网络［13］。网络一般存在四种形态，即规则网络、随机网络、小世界网络和无标度网络。典型的规则网络是指网络中每一个节点只和它周围的邻居节点相连，其具有聚类特性，但不具有较小的平均最短距离；随机网络的度分布可以用Poisson分布表示，即网络不是规则的而是具有某种随机性，最具代表性的为 ER随机网络模型［14］，其具有较小的平均最短距离但无聚类性；小世界网络作为规则网络向随机网络发展的过渡网络，同时具有较小的平均最短距离和聚类性，最具代表性的为 WS小世界网络模型［1］；无标度网络是指网络的度分布符合幂律分布，由于其缺少一个描述问题的特征尺度而被称为无标度网络，具有增长性和偏好依附性，最具代表性的为BA无标度网络模型［2］。四种网络的拓扑示意图如图1所示。

图1 四种网络图拓扑示意图

2 公交网络拓扑特性

Space L方法是公交网络建模最常用的方法［15］，将公交站点视为节点，若两个站点被一条或多条线路顺序通过，且前后相邻，则这两个站点之间存在连边，构建的网络被称为地理空间网络模型。文章选取截止到 2014年 5月的济南市 195条公交线路和1433个站点为样本数据，采用 space L方法对济南市公交网络建模，建模时将上、下行线路站点抽象成无向无权网络，借助 Netdraw软件可视化公交地理空间网络模型，构建的济南市公交网络模型含有1433个站点，1986条连边，其中点越大代表与该站点相连的连边数量越多，如图2所示。同时基于 Matlab软件编写公交网络拓扑参数计算程序，分析济南市公交网络拓扑性质。

图2 济南市公交网络拓扑图

2.1 度及度分布

度表示与站点直接相连的公交站点数。累积度分布表示在网络中任意选出一个站点其度值大于的概率。济南市公交网络站点度值排序统计如表1所示，度值为2的站点所占比例最大，为57.15%，度值大于7的站点不足1%，说明济南市公交站点之间的连接比较稀疏，承担公交网络主要流通、分流的站点为网络中极少部分站点，通常为公交网络的集散站点或枢纽站点。通过计算，得到网络的平均度为2.77，表明每个站点平均有 2～3条公交线路经过，累积度分布符合的幂律分布，故度分布指数。如图3所示，为济南市公交网络累积度分布及其双对数坐标图，使用 Matlab软件对累积度分布的双对数坐标进行拟合，得到其满足线性回归方程 y=-2.802x+1.52，相关性系数 R2=0.8735，进一步说明济南市公交网络累积度分布符合幂率分布，具有无标度网络的特征。表2给出济南市公交网络度值较大的前18个站点，其中省体育中心站具有最大的度值，表明该站点具有最好的路网通达性，为公交网络的一类关键站点。

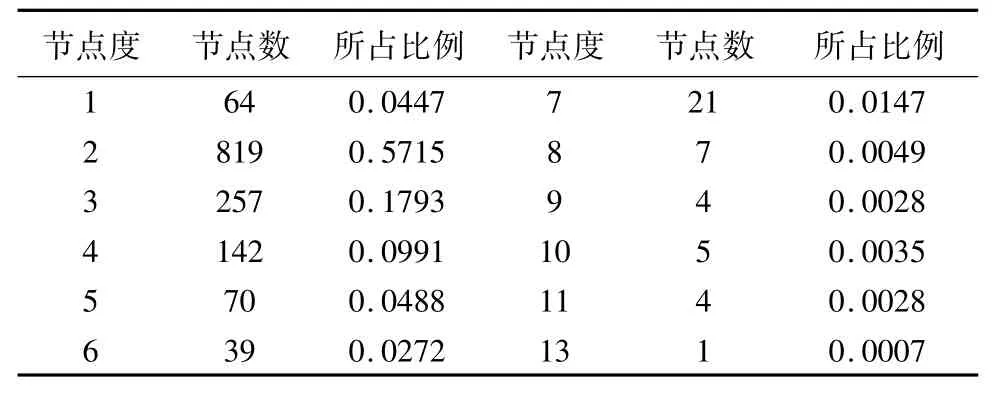
表1 济南市公交网络站点度值排序统计

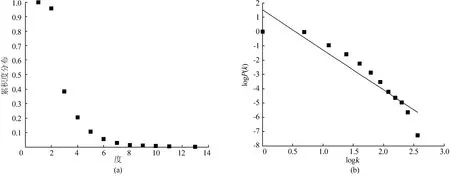
图3 济南市公交网络累积度分布及其双对数坐标图

2.2 平均最短距离

表2 济南市公交网络中高度值站点及其度值

2.3 平均聚类系数

聚类系数反映了公交网络站点的聚集程度，计算方法为：假设站点 i通过 ki条边与 ki个站点相连，那么这 ki个站点都互相连接时最多有ki（ki-1）／2条边，而这 ki个站点之间实际存在的边有Ei条，则站点i的聚类系数 Ci由式（2）确定为

整个网络的聚类系数C定义为所有站点 i聚类系数的平均值，由式（3）表示为

通过计算，得到济南市公交网络的平均聚类系数为0.10，表明济南市公交网络的平均聚类系数较大。较大的聚类系数可以使公交网络在某个站点瘫痪时，对原有直达站点之间的连接不会构成太大的影响，具有较高的容错性。

2.4 介数

站点介数为网络中所有最短路径经过该站点的数量比例，反映了站点在整个网络中的重要程度。站点介数 Bi由式（4）表示为

式中：njk为连接站点 j与站点 k的最短路径的数量，njk（i）为连接站点j与站点k且经过站点的最短路径数量。在进行公交网络规划时，提高介数较大站点的客运量和车辆吞吐性能能够显著提高公交网络的运营效率。表3给出济南市公交网络介数较大的前18个站点，其中省体育中心站具有最大的介数，表明经过该站点的最短路径数量最多，为公交网络的另一类关键站点。

本世纪初当以西北和海上为主体的产区战略接替已打开局面、东部老区已开始显示出壮年阶段后期的许多特征时，一批长期从事勘探的老专家便以多种形式（包括集体向最高领导层上书）提出开展新一轮战略性开拓的问题。鉴于中国石油工业的主体已组成上市公司，建议这项工作宜由国家主持（包括出资）动员全国产学研力量进行。中央适时地决定，由当时的国土资源部新组油气资源发展战略研究中心（后来由自然资源部地质调查局接手）来承担此项工作并取得初步进展。

表3 济南市公交网络中高介数站点及其介数值

2.5 网络有效性

网络有效性与网络通行能力密切相关，是评价网络抗毁性优劣的重要指标。网络有效性E由公式（5）确定为式中：N为公交网络中站点的数量，个；dij为从站点 i到站点 j的最短距离。通过计算，济南市公交网络的有效性为0.075，公交网络中某些站点瘫痪会导致网络有效性的降低。

2.6 网络最大连通率

网络最大连通率是评价网络功能状态和抗毁性的重要指标。网络最大连通子图是指将网络中所有节点用最少边连接起来构成的最大子图，其连通率称为网络最大连通率。在城市公交网络中，当公交网络处于正常状态时，所有站点都互相连通，其最大连通子图的站点数等于整个公交网络的站点数，此时公交网络最大连通率S=1；当公交网络遭受攻击而使部分站点瘫痪时，公交网络被分成若干个互相不连通的子连通图，其中最大连通子图的连通率称为公交网络最大连通率，此时公交网络最大连通率S∈（0，1）。网络最大连通率 S由式（6）确定为式中：N为公交网络中站点的数量，个；N′公交网络最大连通子图的站点数，个。

3 实证分析

3.1 公交网络鲁棒性仿真

公交站点拥堵后，会导致公交网络可靠性降低。在统计分析中，主要表现为网络有效性、平均聚类系数和最大连通率的变化，因此可将公交网络有效性E、平均聚类系数C和最大连通率S作为度量公交网络鲁棒性的指标。根据公交站点失效是否具有选择性，可将攻击方式分为随机攻击（如突发性交通事故引起的交通拥堵）和蓄意攻击（如恐怖袭击）两种，其中蓄意攻击又可分为基于度数的蓄意攻击和基于介数的蓄意攻击。在公交网络鲁棒性仿真中，当站点遭受某种攻击并且失效时，通过删除与该站点相连的所有连边来表示该站点已完全瘫痪。文章基于 Matlab软件编写仿真程序，分析济南市公交网络遭受随机攻击和蓄意攻击时网络有效性E、平均聚类系数 C和最大连通率S的动态演化过程。

如图4所示，在随机攻击下公交网络的有效性下降趋势比较缓慢，具有较强的鲁棒性；在蓄意攻击下网络有效性急剧下降，尤其是按度数的攻击方式对网络有效性的影响最大，即三种攻击方式对网络鲁棒性的影响程度遵循随机攻击＜按介数攻击＜按度数攻击，当按度数去除的站点达到230个时，公交网络已经基本瘫痪。此外，网络平均聚类系数在三种攻击方式下呈现出与网络有效性相似的失效演化趋势，基于度数的蓄意攻击导致公交网络聚类性急剧破坏，恶化了公交网络的小世界特性，如图5所示。

公交网络随着部分站点瘫痪会被分割成若干个子集团，各子集团相互独立，攻击演化进程中计算的网络有效性和平均聚类系数实际是各子集团计算值之和，但各子集团相互独立对公交网络整体通行能力的影响是巨大的，仅以网络有效性和平均聚类系数评价网络鲁棒性优劣是不全面的。如图6所示，基于度数的蓄意攻击导致公交网络最大连通率急剧下降，网络整体性严重破坏，对网络鲁棒性的影响最大；随机攻击与基于介数的蓄意攻击相比，当被攻击站点数在0～250个之间时，随机攻击下网络最大连通率下降较慢，当被攻击站点数达到250个以上时，两种攻击方式对网络最大连通率的影响差别不大。

综上所述，三种攻击方式对公交网络鲁棒性的影响程度遵循随机攻击 ＜按介数攻击＜按度数攻击；公交网络对随机攻击具有鲁棒性，对蓄意攻击具有脆弱性，且基于度数的蓄意攻击对公交网络鲁棒性的影响最大，能够使公交网络急剧失效。究其原因，济南市公交网络作为典型无标度网络，其站点是异质的，基于度数的蓄意攻击对公交网络异质性的影响最大，会造成公交网络连通性的巨大破坏。因此，济南市公交网络具有“既鲁棒又脆弱”的特性，在实际的公交管理运营中要重点控制好度数和介数较大的两类关键站点（见表2、3），即 “hub站点”。

3.2 公交网络鲁棒性优化对策

城市公交系统的健康发展能够有效的吸引客流，降低其他机动车对城市道路交通产生的压力，满足城市化进程中日益增长的交通需求。研究表明，交通网络拓扑结构对交通拥堵及其传播具有重要影响。因此，通过对公交网络拓扑结构进行优化，提高公交网络的鲁棒性。

（1）公交网络中度数较大的站点（见表2，省体育中心站、辛西路北口站、天桥南站等）是关键站点，控制关键站点可以提高整个公交网络的运输能力。在公交网络规划时，新设线路应避开度数较大的站点；在公交网络改造时，增设区域枢纽站点，降低此类关键站点的承载压力，提高公交网络的同步能力和鲁棒性。

（2）介数较大的站点（见表 3，省体育中心站、千佛山站、省立医院东院站等）是公交网络的另一类关键站点，站点介数越大说明经过该站点的最短路径条数越多。因此，在公交网络改造时，应选取连接介数较大的站点设置快速公交新干线，作为区域公交系统的中枢线路，利用少数几条快速公交线路替换多条重复的公交线路，使公交网络达到快速、高效、容易疏导的优良状态。

（3）“定制公交”是公交网络优化的有效方法，其客流主要由较大的居民小区、职工宿舍区的早、晚通勤出行引发。为消化这部分客流对常规公交网络的影响，可以设置早、晚特定时段的公交专用线满足这部分出行需求，即设置定制公交。其运行线路可以是主干路、次干路甚至是支路，这种临时直达线路降低了局部网络的平均最短距离，优化了公交网络的小世界特性。

图4 三种攻击方式下的公交网络有效性图

图5 三种攻击方式下的公交网络平均聚类系数图

图6 三种攻击方式下的公交网络最大连通率图

4 结论

通过研究可知：

（1）分析space L方法构建的济南市公交地理空间网络模型的拓扑性质，得到济南市公交网络具有较小的平均最短距离和较大的聚类系数，累积度分布符合幂律分布特征，是具有小世界特征的无标度网络。

（2）济南市公交网络在站点出现随机故障时具有较好的鲁棒性，当站点遭受到蓄意攻击时的鲁棒性较差，其中按度数去除的蓄意攻击对网络鲁棒性的影响最大，当按度数去除的站点达到230个时，公交网络已经基本瘫痪，即具有“既鲁棒又脆弱”的特性；以复杂网络理论为基础，给出复杂公交网络鲁棒性的优化对策，为城市公交网络的规划、改造提供理论依据。

［1］ Watts D.J.，Strogatz S.H..Collective dynamics of small-world networks［J］.Nature，1998，393：440-442.

［2］ Barabasi A.L.，Albert R..Emergence of scaling in random network［J］.Science，1999，286：509-512.

［3］ 张晋，梁青槐，贺晓彤.北京市地铁网络拓扑结构复杂性研究［J］.北京交通大学学报，2013，37（6）：78-84.

［4］ Fu B.B.，Gao Z.Y.，Liu F.S.，et al.Express passenger transport system as a scale-free network［J］.Modern Physics Letters B，2006，20（27）：1755-1761.

［5］ 曾小舟，唐笑笑，江可申.基于复杂网络理论的中国航空网络结构实证研究［J］.交通运输系统工程与信息，2011，11 （6）：175-181.

［6］ 许晴，祖正虎，徐致靖，等.330个中国城市P空间下公交复杂网络实证研究［J］.交通运输系统工程与信息，2013，13 （1）：193-198.

［7］ Wu J.J.，Gao Z.Y.，Sun H.J..Urban transit system as a scale-free network［J］.Modern Physics Letters B，2004，18 （19）：1-7.

［8］ Von Ferber C.，Holovatch T.，Holovatch Y..Attack vulnerability of public transport networks［J］.Traffic and Granular Flow，2007，20：721-731.

［9］ Berche B.，Von Ferber C.，Holovatch T.，et al.Resilience of public transport networks against attacks［J］.The European Physical Journal B，2009，71（1）：125-137.

［10］汪涛，吴琳丽.基于复杂网络的城市公交网络抗毁性分析［J］.计算机应用研究，2010，27（11）：4084-4086.

［11］王波，柯红红，蒋天发.基于复杂网络理论的杭州公交网络建模与特性分析［J］.武汉大学学报（工学版），2011，44（3）：404-408.

［12］郑啸，陈建平，邵佳丽，等.基于复杂网络理论的北京公交网络拓扑性质分析［J］.物理学报，2012，61（19）：5101-51010.

［13］吴建军，高自友，孙会君，等.城市交通系统复杂性—复杂网络方法及其应用［M］.北京：科学出版社，2010.

［14］Erdos P.，Renyi A..On the evolution of random graph［J］.Publications of the Mathematical Institute of the Hungarian Academy of Science，1960，5：17-60.

［15］Sienkiewicz J.，Holyst J.A..Statistical analysis of 22 public transport networks in Poland［J］.Physical Review E，2005，72 （4）：127.

（学科责编：李雪蕾）

Emprical research on topological properties and robustness of urban public transit network

Zhang Lin1，Fu Baibai2*，Yin Zengchao2
（1.School of Transportation Engineering，Shandong Jianzhu University，Jinan 250101，China；2.School of Architecture and Urban Planning，Shandong Jianzhu University，Jinan 250101，China）

The topological properties and robustness are two important aspects to evaluate the reliability of urban public transit network.In this paper，195 bus routes and 1433 bus stations of Jinan city until May 2014 have been collected as sample date to build up Jinan city's public transit geospatial network model by applying space L method.Then，topological properties，which include degree，average shortest distance，average clustering coefficient，betweenness，network efficiency and network largest connectivity ratio are analyzed.Furthermore，empirical analysis of robustness of public transit network is carried out.Finally，robustness optimization strategies according to Jinan city's public transit network are proposed.The results show Jinan city's public transit network has smaller average shortest distance and larger clustering coefficient，and its degree distribution follows power-law distribution with index λ=2.112，i.e.，it is a scale-free network with small-world characteristics.The public transit network shows good robustness under random attacks，but robustness is comparatively poor under deliberate attacks，and the deliberate degree attacks have the largest impact on robustness of public transit network.

complex public transit network；space L method；topological properties；robustness；optimization strategies

N94；U121

A

1673-7644（2015）03-0243-06

2015-01-11

国家自然科学基金项目（71171124）；国家自然科学基金项目（71371026）；国家自然科学基金项目（71471104）；山东省高校科技计划项目（J14LI02）；山东省高等学校教学改革项目（2012295）

张琳（1990-），男，在读硕士，主要从事交通运输系统建模与仿真等方面的研究.E-mail：zhang_lins＠hotmail.com

*：傅白白（1961-），女，教授，博士，主要从事城市交通规划理论与方法等方面的研究.E-mail：fubaibai＠163.com