基于小波变换的光纤陀螺降噪预处理技术

刘玉霞，李拉成，张 鹏

（陕西宝成航空仪表有限责任公司 陕西 宝鸡 721006）

基于小波变换的光纤陀螺降噪预处理技术

刘玉霞，李拉成，张 鹏

（陕西宝成航空仪表有限责任公司 陕西 宝鸡 721006）

为了实现对光纤陀螺输出数据进行降噪，使输出数据能真实反映陀螺数据的目的，提出了一种基于小波变换的光纤陀螺降噪预处理技术。文中研究了小波变换及Birge-Massart算法，设计了基于小波变换的光纤陀螺的降噪预处理方法，利用该方法，对实测的光纤陀螺数据进行仿真试验。试验结果表明：用小波变换进行降噪处理具有良好的效果。

光纤陀螺；小波变换；Birge-Massart；阈值

光纤陀螺在小型、低功耗、长寿命、高可靠性、快速启动、批量化生产等方面更有优势，所以受到了世界各国的重视且发展迅速，正逐步取代传统经典力学陀螺而成为惯性导航系统的关键元件[1-2]。在光纤陀螺信号输出过程中，通常有高斯型的光源相对强度噪声、光电探测器引入的具有泊松分布的散粒噪声、探测器跨阻抗放大器反馈电阻的热噪声、放大器输入电流与输入电压引入的噪声等，这些噪声将影响光纤陀螺捷联惯导系统的导航精度。因此，研究光纤陀螺数据降噪预处理是非常必要的[3-4]。

光纤陀螺信号往往是由多种频率分量组成。当信号变化剧烈时，为了得到更多的频率信息，需要一个较短的时间窗描述其局部行为；当信号变化平缓时，需要一个长的时间窗描述其整体行为，即希望有一个灵活可变的时间窗。小波变换由于具有良好的时频局部化能力和多分辨率分析特性[5]，一方面能将信号在多个尺度上进行小波分解，而各尺度上分解得到的小波变换系数代表原信号在不同分辨率上的信息，由于信号和随机噪声在不同的尺度上进行小波分解时，存在着不同的传递特性；另一方面，能同时在时频域中对信号进行分析，故它能有效地区分光纤陀螺信号中的突变部分与噪声，从而实现信号的降噪。因此，本文研究了小波变换及Birge-Massart算法，设计了基于小波变换的光纤陀螺降噪预处理方法，利用该方法，对实测的光纤陀螺数据进行仿真试验。试验结果表明：将小波变换用于光纤陀螺测量值预处理过程中，既有效地降低了光纤陀螺输出噪声，同时也提高了信噪比，用小波变换进行降噪处理具有良好的效果。

1 小波变换及降噪

1.1 小波变换

设Ψ(t)∈L2(R)（L2(R)属于平方可积的实数空间），其傅里叶变换为Ψ(ω)，当Ψ(ω)满足以下允许条件：

时，称Ψ(t)为一个基本小波或小波母函数。将母函数Ψ(t)通过伸缩和平移后，产生一个函数族Ψa，b(t)：

其中，a，b分别为伸缩因子和平移因子。

对于任意的函数f(t)=L2(R)的连续小波变换为

其逆变换为：

在实际应用中一般对变换进行二进制离散，即取a=2j，k=b/a则Ψa，b(t)表示为Ψj，k(t)=2-j/2Ψ(2-jt-k)，相应的离散小波变换公式为：

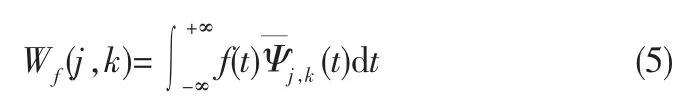
称Ψj，k为二进小波，j为二进小波的尺度。

1.2 小波降噪

一个含噪的一维信号模型可以表示为：

其中s(t)为含噪声信号，f(t)为有用信号，σ为噪声强度,一般假设σ=1,e(t)为噪声信号。小波变换的目的是要抑制e(t),以恢复f(t)。

在这个噪声模型下，用小波分析对信号降噪的过程如图1所示。

图1 小波降噪过程模型Fig.1 Wavelet denoising process model

图1中各项的具体形式为：

1)原始信号f；

2)噪声信号w；

以上两项相当于式(6)中的信号和噪声项。

3)信号在小波域的表示LΨ，即原信号（含噪声）在小波变换下的分解系数；

4)阈值算子Fδ：阈值算子作用以后，模值小的系数被置为零，只保留模值大的系数项；

5)掩码算子M：掩码算子作用的结果是保留特定的系数并把其他的系数置为零。

信号降噪的过程如下：

1)对信号进行小波分解，一般情况下，有用信号f(t)表现为一些相对比较平稳的信号或者是低频信号，而噪声信号e(t)通常情况下表现为高频信号，故可利用门限阀值等形式对所分解的小波系数进行处理；

2)对信号进行小波重构即可达到对信号降噪的目的。

2 小波变换用于光纤陀螺信号降噪过程

2.1 小波系数分解过程

根据多尺度分析方法，用小波变换对初始信号S分解处理。将S分解为两个部分，即cA1和cD1，cA1保留原信号的低频信息或近似信息，而cD1保留信号高频信息或细节信息。从噪声过滤看，cA1信号有效成分多，cD1属噪声信息。对cA1信号小波分解，得cA2、cD2。对cA2再分解得cA3和cD3，可多次分解，如图2所示。

其信号的多尺度数学分解过程如下：

1)尺度函数φ(t)、Ψ(t)经过平移伸缩后有

图2 小波分解树结构图Fig.2 Wavelet structure diagram

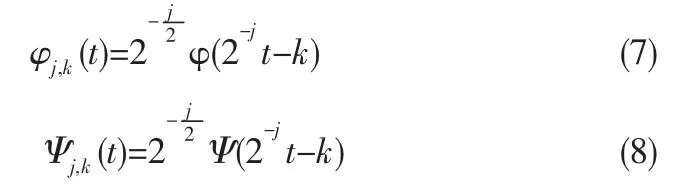
上式分别表示在不同尺度j下，随着k的位移，张成不同的尺度空间和小波空间。

2)信号s(t)可分解为

式中cj,k和dj,k分别为j尺度空间的尺度系数和小波系数。

2.2 阈值处理过程

小波变换降噪过程中核心的步骤就是对信号经过小波分解后的系数确定阈值。阈值的选取直接影响降噪的质量，因此，确定各层阈值成为降噪过程中最重要的任务。

从原始信号确定各层阈值有几种方法，文中选择Birge-Massart策略确定阈值方法。Birge-Massart算法是由j，M和α3个参数定义的，具体步骤如下：

第一步：给定一个指定的分解层数j，对j+1以及更高层，所有系数保留；

第二步：对第i层(1≤i≤j)保留绝对值最大ni的个系数,ni由下式确定：ni=M(j+2-i)α，其中M和α是经验系数，缺省情况下取M=L(1)，也就是第一层分解后系数的长度，一般情况下L (1)≤M≤2L(1)，α的取值在去噪情况下一般取1.5～3。文中取α=1.5，M=1.3L(1)来求得各层阈值。

2.3 光纤陀螺信号重构过程

光纤陀螺信号重构过程与信号分解过程相似，只是方向相反，在对小波分解系数进行阈值处理后，再根据（9）式恢复降噪后的信号。

3 光纤陀螺数据小波降噪仿真实验及分析

试验数据为项目组采集的光纤陀螺输出数据，数据包括每个采样时刻东向、北向、天向的陀螺原始输出数据。采样频率为100 ms，采样时间6 min，共采集了3 600个值。试验数据有很多份，任取一次光纤陀螺输出数据作为实测数据，然后用小波分解对实测光纤陀螺输出进行二维分解、重构并实现小波降噪，试验结果如图3、图4和图5所示。在图3、图4和图5中上图分别为光纤陀螺天向、东向和北向原始测量值，下图为经过小波预处理后光纤陀螺陀螺天向、东向和北向测量值。

从图3、图4和图5可以看到，不论是天向、东向还是北向，利用小波降噪后光纤陀螺的测量值的形状与原始数据非常相似，而且明显看到降噪后的数据更加平滑和收敛。

为了分析降噪后光纤陀螺的测量值与原始测量值的偏差程度，以原始陀螺输出值作参考标准，引入误差方差作为性能指标，其定义如下：

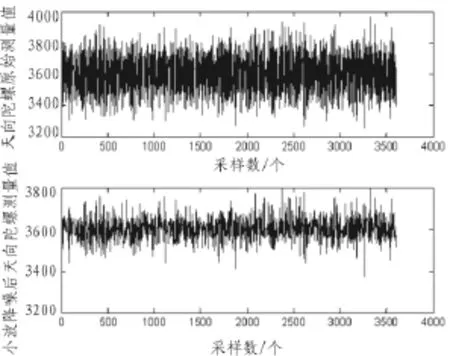
图3 天向陀螺测量值和小波降噪后测量值对比图Fig.3 Up-axis gyro measurements and wavelet denoised comparison

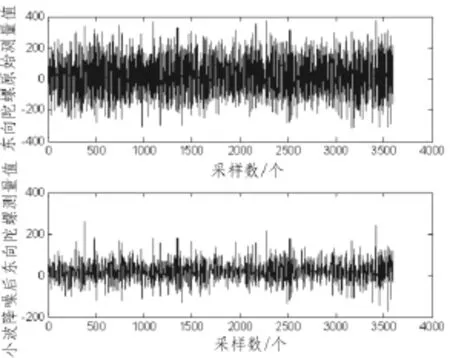
图4 东向陀螺测量值和小波降噪后测量值对比图Fig.4 East-axis gyro measurements and wavelet denoised comparison

图5 北向陀螺测量值和小波降噪后测量值对比图Fig.5 North-axis gyro measurements and wavelet denoised comparison

其中，δi为每个采样点的某个方向的光纤陀螺的测量值，σi为相应采样点降噪后点的光纤陀螺的测量值，n为总试验测点数目。经计算，基于小波变换降噪后天向、东向和北向标准差分别为1.454 1、1.527 6和2.069 5。可见，光纤陀螺天向、东向和北向偏差不大，没有使原测量数据失真，而且小波分析法在降噪的同时，很好地保持了原始测量数据的特性，说明对于光纤陀螺的测量值，用小波变换进行降噪处理是可行的。

为了衡量小波变换用于光纤陀螺测量值预处理的效果，引入标准差作为性能指标，因为样本的标准差反映了一个样本集合总体上偏离其平均水平的程度，所以光纤陀螺测量值标准差描叙了围绕聚集中心的偏差，对描述小波变换用于光纤陀螺测量值预处理效果是有效的。标准差的计算公式如下：

4 结论

文中利用小波分析对光纤陀螺测量数据进行降噪处理，对实测的光纤陀螺数据进行仿真试验。实验结果表明：将小波变换用于光纤陀螺测量值预处理过程中，既有效地降低了光纤陀螺输出噪声，同时也提高了信噪比，用小波变换进行降噪处理具有良好的效果，适于在初始对准前对光纤陀螺输出数据的预处理。

[1]王巍.光纤陀螺惯性系统 [M].北京：中国宇航出版社，2012.

[2]Dandridge A.Fiber-optic sensors make waves in acoustics, control,and navigation [J].Circuits and Devices Magazine, IEEE,1990,6(6):12-19.

[3]Pandit S M,Zhang W.Modeling random gyro drift rate by data dependent systems[J].IEEE Transactions on Aerospace and Electronic Systems,1986,22(4):455-460.

[4]James Good Win.Progress of fiber optic gyroscope development for space application[C].AAS00-043,23rd annual AAS guidance and control conference,2000,425.

[5]董长虹，高志，余啸海.小波分析工具箱原理与应用[M].北京：国防工业出版社，2004.

[6]谢仕民，王子静，钟钧宇，等.小波降噪技术在地磁数据库与处理中的应用研究[J].战术导弹控制技术，2008(2):15-18. XIE Shi-min,WANG Zi-jing,ZHONG Jun-yu,et al.A research on the application of wavelet de-noising technique [J].Control Technology of Tactical Missile,2008(2):15-18.

A technique of FOG de-noising pretreatment based on wavelet transform

LIU Yu-xia,LI La-cheng,ZHANG Peng
（AVIC Shannxi Baocheng Aviation Instrument CO.,LTD,Baoji 721006，China）

In order to realize the de-noising of fiber optic gyro output value,so that the measured value can reflect the true purpose,A technique of FOG de-noising pretreatment based on wavelet transformation is presented.The paper studies the wavelet transform and Birge-Massart algorithm,design the method of fiber optic gyroscope de-noising pretreatment based on wavelet transform.The actual measurement data was simulated by the proposed method.The experiment shows that the technique has good performance,and achieves the de-noising purpose.

fiber optic gyro;wavelet transform；birge-Massart；threshold value

TN274

A

1674-6236（2015）07-0093-03

2014-08-03 稿件编号：201408008

刘玉霞(1981—)，女，山西朔州人，博士，工程师。研究方向：导航、制导与控制。