基于单相R744喷射器系统的引射比计算模型及其实验验证

熊杰，王如竹*，EIKEVIK Trygve Magne

（1-上海交通大学制冷与低温工程研究所，上海 200240；2-挪威科技大学，特隆赫姆 7491）

基于单相R744喷射器系统的引射比计算模型及其实验验证

熊杰1，王如竹*1，EIKEVIK Trygve Magne2

（1-上海交通大学制冷与低温工程研究所，上海 200240；2-挪威科技大学，特隆赫姆 7491）

本文在现有引射比计算模型的基础上，建立了一个针对单相R744喷射器系统的混合模型。首先通过流体力学和传热学基本原理得到引射比的理论方程，然后在充分考虑喷射器入口和出口流体状态的基础上，对该方程进行简化后得到一个新的计算模型。该模型具备五个待定参数，文中也给出了待定参数的拟合方法。计算结果与实验结果的对比表明该新模型具有较高的精度。

喷射器；引射比；计算模型；R744

0 引言

制冷系统的优化与改进一直是近年来制冷领域研究的热点，研究人员采用多种多样的方式来提高制冷系统的效率，达到节能、环保等目的[1]。在很多工业过程中，燃烧过程释放出的相当一部分热量最后是通过废热的形式排放到环境中去，产生了大量的浪费。因此，对废热进行回收利用，减少对化石燃料的消耗，不仅能够产生经济效益，还可以降低对环境的负面作用[2-3]。使用喷射器进行膨胀功回收便是一种很有前途的改善制冷系统的方式，喷射器是一个静态组件，没有任何移动部分，不需要特别的润滑措施，这样的系统稳定、安全、可靠[4-5]。

近年来，国内外针对喷射器进行了多方面的研究，主要的研究方式为实验探究和数值分析以及二者的结合。葛研军等[6]基于热力学原理，分析了喷射器内部工作流体和引射流体相互作用过程中能量变化的情况，建立了制冷系统三大部件——喷射器、蒸发器和冷凝器的热力学模型，并通过Matlab软件的仿真计算，探究了工作流体压力、冷凝温度和蒸发温度对引射比的影响，并给出了使得系统具有良好经济性的工作参数。祝银海等[7]建立了一个可用于喷射器实时控制及优化的简单且有效的混合模型（基于热力学、流体力学相关理论建立引射比基本方程，并采用二位函数近似引射流的速度分布，经过简化、数值分析获得此模型），并且采用R141b制冷系统进行了实验验证，结果表明该模型能够在一定范围内精确预测喷射器引射比。

二氧化碳R744的特殊性质及环境价值使其具备很好的应用潜力，采用R744作为制冷工质也渐渐成为研究的热点。针对R744系统的研究主要集中于跨临界系统，亚临界循环相对较少[8-10]。BANASIAK K和HAFNER A[10]提出了一个针对二相R744喷射器系统的一维仿真模型：模型建立了质量、动量和能量守恒的控制方程，并被证实适用于较大范围的工作条件。CHRISTIAN L等[11]通过实验比较了二相R744喷射器系统与标准的传统R744膨胀阀系统的效率：通过对一系列不同的蒸发压力和空气冷却器出口温度进行控制测试，并对喷射器的效率、引射比和压力恢复情况进行记录，结果表明喷射器效率及系统COP比传统系统分别提高了22%和17%。

然而，至今针对单相R744喷射系统的研究还相当单一，主要是通过数值分析方法建立一定的仿真模型。尽管单相喷射器和二相喷射器在结构和尺寸上没有本质区别，但是国内外几乎没有单相喷射器系统实验分析的报道。本文便是通过对现有的引射比计算模型进行优化，并通过实验测试数据的对比，获得了较高精度的基于单相R744喷射器系统的引射比计算模型。

1 单相R744喷射器及喷射器系统介绍

1.1 喷射器概述

喷射器作为喷射制冷系统的核心部件，是工作流体和引射流体相互作用的场所，在其内部经历了复杂的混合、压力恢复过程。图1给出了一个典型喷射器的各部分结构分布图[11-14]。

如图1所示，一个典型的喷射器可以包含四部分：喷嘴部分、引射部分、混合扩压部分和出口部分。首先，高压的工作流体（驱动流体）在管嘴进口膨胀并在出口成为超音速流体，超音速流体的流动在引射区域和混合区的进口部分产生了一个局部低压区，因低压区与引射流体的压强差而产生的驱动力牵引来自蒸发器的引射流体（被动流体）进入引射区。然后，工作流体和引射流体在混合区进行混合，经历一个压强恢复的过程，这是由于工作流体膨胀所导致的“汇聚”效果；有时甚至在混合区的某些管道截面部分引射流体达到声速并产生阻塞现象，这个理论假设的截面被称作“有效截面”，并且位置不是固定的，随工作条件和参数的改变发生移动。

图1 喷射器各部分结构分布图

SUN D W等[3]研究发现，真正意义上的混合开始于引射流体阻塞之后，混合过程会导致引射流体的加速和工作流体的减速；在混合区的末端，工作流体和引射流体已经充分混合，静压强往往被假定为恒定，直至进入混合区的喉部后产生激波现象，然后进一步在扩压区中产生对流体的“压缩”效果，同时伴随着流体速度的骤降（超音速到亚音速）。

图2给出了系统所用喷射器的结构及参数配置，后文的模型便是建立在此图的基础上；表1也给出了具体的尺寸参数值。

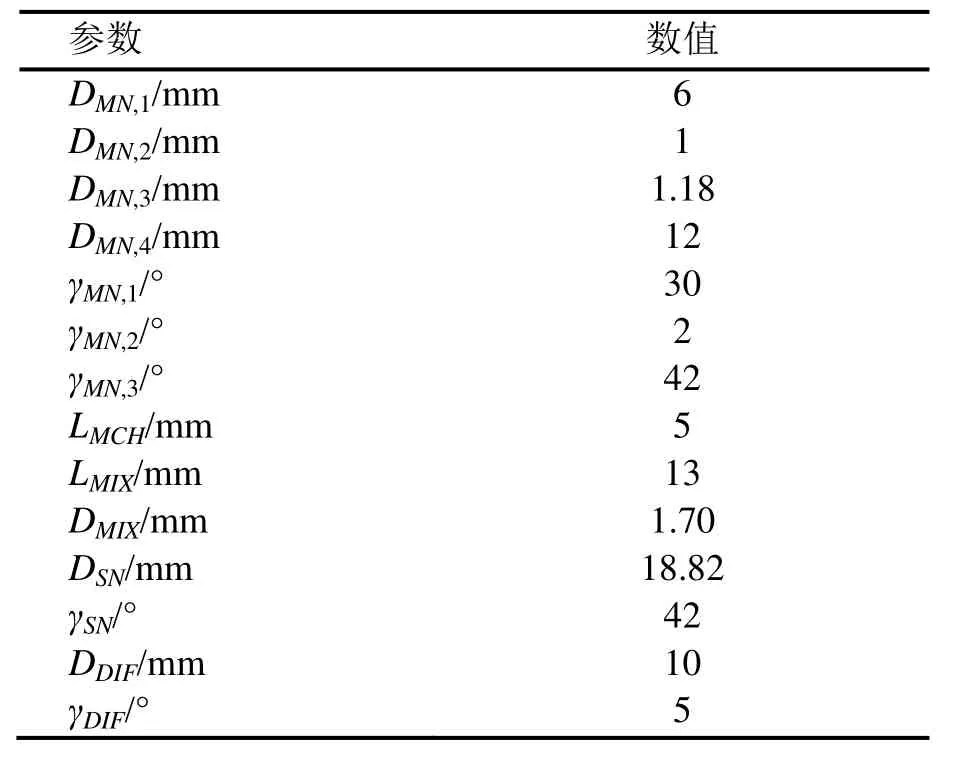
表1 喷射器具体尺寸配置

图2 喷射器尺寸配置图

1.2 喷射器系统介绍

图3为一个小容量的R744单相喷射器系统，该系统的主要部件包括喷射器、冷凝器、循环泵、发生器、膨胀阀和蒸发器。R744工作流体在蒸发器中吸热气化后，进入喷射器与引射流体相互作用后经过冷凝器液化，一部分通过膨胀阀进入蒸发器产生制冷效果，另一部分经过循环泵后进入蒸发器。

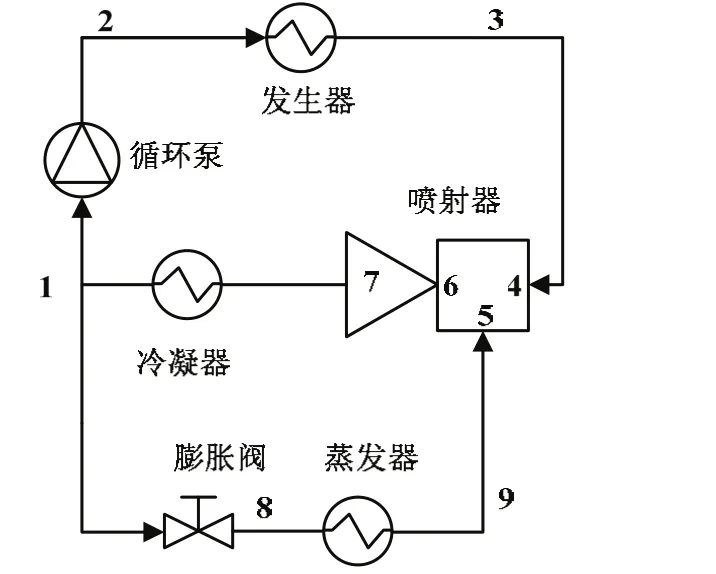
图3 R744单相喷射器系统

2 喷射器仿真计算模型建立

依据流体力学与传热学相关理论，通过建立质量守恒、动量守恒和能量守恒的基本控制方程构建的计算模型相当复杂，在实践中不易操作。ZHU Y H等[15]依据上述理论，建立了一个简化的二维计算模型，不失一般性地作了以下假设：

1) 工作流体为理想气体，具有稳态性质，管道内壁绝热；

2) 工作流体在喷射器内部径向均匀分布；

3) 引射流体的压强和温度在径向均匀分布；

4) 图2中LMCH/DMIX超过1.5，使得工作流体充分膨胀且引射流体充分加速，保证引射流体在混合区发生阻塞现象；

5) 引射流体在引射区域的压强均匀分布且等于其进口压强；

6) 用等熵关系来计算摩擦损失。

2.1 工作流体和引射流体计算

工作流体的流量计算已经提出了很多模型，HUANG B J等[16]提出了一个比较精确而且适合本系统的一维模型，其控制方程如下：

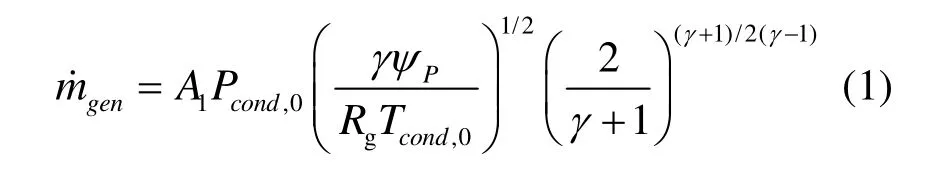
式中：

A1——直径为DMN,1处的截面积；

Pcond,0——发生器内流体静压强（即喷射器入口处压强）；

Tcond,0——发生器内流体温度（即喷射器入口处温度）；

γ——热容比；

ΨP——等熵系数；

Rg——气体常数。

利用能量守恒方程及等熵流动原理，得到工作流体从喷嘴入口到混合区入口的关系表达式：

式中：

M1——喷嘴出口的马赫数；

T1——喷嘴出口的温度；

V1——喷嘴出口的速度；

ζ——混合系数。

M1的计算式为：

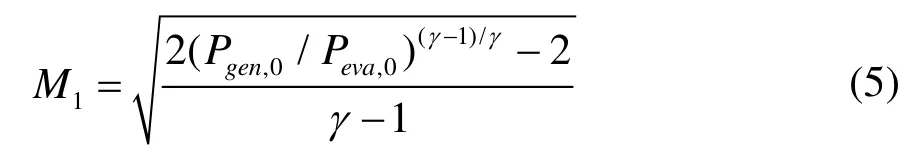
其中Peva,0为蒸发器中引射流体压强。

引射流体在喷射器内流动，由于流体黏性会沿着壁面形成一个速度边界层。根据前述假设，定义引射流体在混合区入口处的速度分布为[13]：

其中n为引射流体速度分布函数指数，其计算公式为：

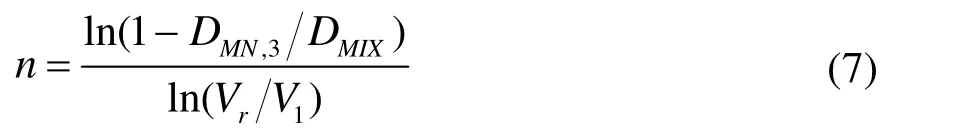
为了计算n的确切值，要用到该模型的一个重要假设：阻塞临界圆[15]。临界圆半径为R0=DMN,3/2，“阻塞临界圆”的速度恰好为临界速度，根据式(4)，可知马赫数正好为1。因此可以将算式(7)简化为：

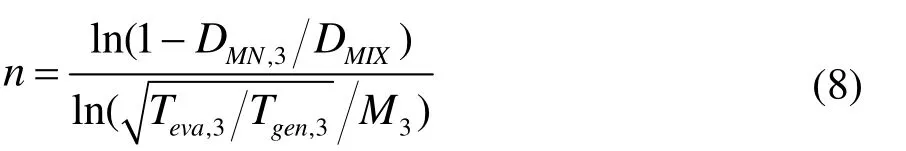
其中Teva,3、Tgen,3与M3分别为工作流体在混合区入口的温度，引射流体在混合器入口的温度和马赫数。进一步考虑到临界圆存在于工作流体与引射流体混合区之间的一个薄层，而且两股流体接触充分，可进一步假设混合处温度相同，n的计算式可进一步简化为：

于是引射流体的流量计算为：

最终引射流量计算式为

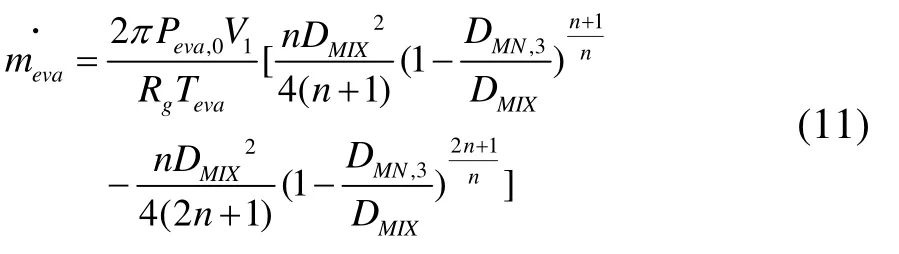
结合式(1)和式(11)，可得引射比计算公式为：

式(12)给出了引射比Φm与喷射器尺寸、工作条件和工质之间的一个关系式，此式可以作为喷射器仿真和性能评估的一个参考，但是也存在以下问题：有的参量如V1和n不能直接测得，需要通过求解状态方程得到；另外涉及参数较多，计算不方便，不利于实际计算与判断。为此，本文考虑到实验中只能测得一些宏观的温度、压强及尺寸等直接条件，结合ZHU Y H等[15]提出的改进办法，在此基础上进一步简化以上模型。

2.2 喷射器计算模型简化

针对上述的计算模型，进一步简化的方向为消除式(12)不可测的参数，这样可行的原因是：流体的物性和状态量在喷射器内部的变化过程并不是很剧烈，通过大量可靠的实验数据的代入优化，完全可以降低流体自身性质的变化对模型的影响。

将式(2)、式(5)和式(9)三式代入式(12)可得到引射比Φm的总计算式：

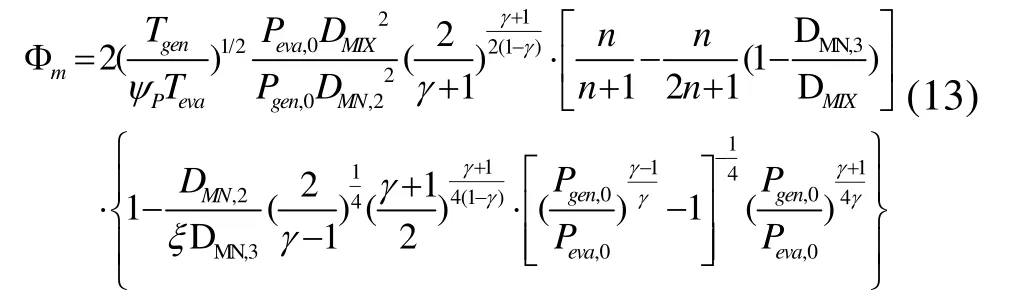
对于一个确定的喷射器，系数ζ和ΨP变动不大，可以简化为常数处理，因此可令：

此式便是本文导出的一个Φm初步计算模型。考虑到上式中存在Teva，蒸发器内部流体往往处于饱和态，温度基本不变，如果用喷射器出口温度Tcond来代替更具现实意义，喷射器出口温度即为冷凝器入口温度。本实验台中冷凝器也工作在饱和态，冷凝器内部流体的温度与冷凝器压强紧密联系，直接用可以控制冷凝器的压强Pcond直接来代替。至于Teva与Pcond两个量之间复杂的转换关系完全可以通过系数μ1和μ5的作用消除，作这样的替换和简化不仅更符合实际情况，而且大大方便计算。

这样，引射比Φm的计算就转化为计算拟合出以上五个参数值：μ1、μ2、μ3、μ4、μ5，然后代入对应的工况条件即可方便的计算引射比。文献[7]中是单独计算μ4并忽略了μ5，本文将这些因素都考虑进来。这样做避免了过多考虑工作流体和引射流体的混合系数以及工况的影响，因为混合系数往往不易确定而且工况也会在系统运行的过程中产生波动。

2.3 参数的拟合

对式(18)两边取对数可得：

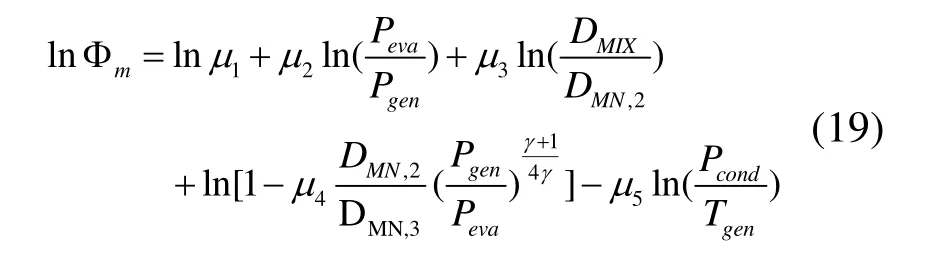
需要说明的是，式(18)和式(19)可用于所有符合要求的喷射器，只需要代入喷射器相关参数以及工况即可。分析上式，可以发现不仅涉及到了喷射器的自身尺寸，还考虑到了工况如蒸发器控制压强、发生器温度、压强及冷凝器控制压强，蕴含了喷射器尺寸、进口和出口的所有状态，符合实际情况，而且五个待定系数的存在也分配了各个因素的权重，从理论上而言有很好的适应性，后文将对该仿真模型的精度进行验证。在本实验中，代入喷射器尺寸参数和R744的γ，化简上式得到：

随机选取一部分Φm实验数据点（反复实验测试得到），利用Matlab拟合这些数据点，并进行反复修正，得出以上五个待定参数值。五个参数μ1、μ2、μ3、μ4和μ5的值分别为：0.8754813、-0.2290646、1.2524347、0.9329751和0.0184036。表2中也给出了拟合后Φm的比较值及误差情况：数据的拟合误差最大不超过6.6%。

表2 参数拟合所用数据表

3 仿真计算结果与实验测量值的对比

前文已经拟合得到了五个待定系数的数值，代入四个状态参数值：发生器出口压强、温度数值和蒸发器、冷凝器的控制压强，得到Φm的模型计算拟合。表3给出了Φm实验测量值与拟合值的比较结果以及相应的状态参量。

表3 Φm模型计算结果与实验数据的比较

模型与四个状态参数有关，在表3中有选择性地选取了12个数据：保持三个状态量不变，第四个状态量选取三个数据点，因此一共12个比较点。Φm实验值、拟合值和相对误差如表3所示，图4和5给出了Φm实验测量值和拟合值的对比以及相对误差情况。观察表3、图4和图5，发现模型拟合的最大相对误差不超过8%，从而充分证明了该计算模型具有较高的准确度。

图4 实验测量值与模型拟合值的对比

图5 模型拟合值对实验测量值的相对误差

由于引射比Φm是计算喷射器效率和系统COP的基础，因此针对Φm的仿真模拟是有意义的，对于设计系统很有参考价值。当具备了比较精确的引射比Φm仿真计算模型，便可以依据确定工况条件，参考压焓图计算喷射器效率和系统COP的数值，从而对整个系统进行详细的设计。

4 结论

本文通过对文献提出的模型进行优化和改进，建立了一个针对R744制冷剂的引射比Φm的计算模型。通过实验所测得的数据对该模型进行拟合，得出适合本喷射器的五个待定系数值μ1、μ2、μ3、μ4、μ5，然后进行Φm预测计算并与实验结果对比，发现此模型最大误差不超过8%，从而证明该模型具有较高的精度。

另外，该模型具备五个变化的待定系数μ1、μ2、μ3、μ4、μ5，在制冷剂、喷射器尺寸和工况条件发生变化时，只需要采用Φm的实验数据对模型进行拟合计算，得出待定系数值后便可以使用该模型进行未实验工况的分析计算和系统设计，因此该Φm计算模型也具备广泛的适应性。

参考文献：

[1] SUMERU K, NASUTION H, ANI F N. A review on twophase ejector as an expansion device in vapor compression refrigeration cycle [J]. Renewable and Sustainable Energy Reviews, 2012, 16(7): 4927-4937.

[2] 马国强, 陶乐仁. 太阳能喷射式制冷系统的实验研究[J].制冷技术, 2014, 34(5): 1-4.

[3] SUN D W, EAMES W. Recent developments in the design theories and applications of ejectors: a review [J]. Journal of the Institute of Energy, 1995, 68(475): 65-79.

[4] 吴迎文, 梁祥飞, 郑波, 等. 单相喷射器内二维流场数值模拟与结构设计[J]. 制冷技术, 2013, 33(3): 52-55.

[5] ELBEL S. Historical and present developments of ejector refrigeration systems with emphasis on trans-critical carbon dioxide air-conditioning applications [J]. International Journal of Refrigeration, 2011, 34(7): 1545-1561.

[6] 葛研军, 阳俊, 葛强. 蒸汽喷射式制冷系统模型建立与仿真[J]. 低温与超导, 2011, 39(11): 48-52.

[7] 祝银海, 厉彦忠, 鱼剑琳. 基于制冷剂R141B的喷射器混合模型及其实验验证[J]. 化工学报, 2008, 59(9): 2188-2193.

[8] PETRENKO V O, HUANG B J, IERIN V O. Designtheoretical study of cascade CO2sub-critical mechanical compression/butane ejector cooling cycle [J]. International Journal of Refrigeration, 2011, 34(7): 1649-1656.

[9] 郭兴龙, 宋新南, 胡自成. 膨胀机与喷射器跨临界二氧化碳循环比较研究[J]. 制冷技术, 2012, 32(2): 53-56.

[10] BANASIAK K, HAFNER A. 1D computational model of a two-phase R744 ejector for expansion work recovery [J]. International Journal of Thermal Sciences, 2011, 50(11): 2235-2247.

[11] CHRISTIAN L, JUERGEN K. Experimental investigation of the COP improvement of a refrigeration cycle by use of an ejector[J]. International Journal of Refrigeration, 2012, 35(6): 1595-1603.

[12] BERGANDER M J. Refrigeration cycle with two-phase condensing ejector[C]// International Refrigeration and Air Conditioning Conference, Purdue: Purdue University, 2006: 1-8.

[13] 索科洛夫, 津格尔. 喷射器[M]. 黄秋云, 译. 北京: 科学出版社, 1977.

[14] BANASIAK K, HAFNER A. Experimental and numerical investigation of the influence of the two-phase ejector geometry on the performance of the R744 heat pump[J]. International Journal of Refrigeration, 2012, 35(6): 1617-1625.

[15] ZHU Y H, CAI W J, WAN C Y, et al. Shock circle model for ejector performance evaluation[J]. Energy Conversion and Management, 2007, 48(9): 2533-2541.

[16] HUANG B J, CHANG J M, Wang C P, et al. A 1D analysis of ejector performance [J]. International Journal of Refrigeration, 1999, 22(5): 354-364.

Mathematical Model and Experimental Validation for Mass Entrainment Ratio of Ejector System with Single Phase R744

XIONG Jie1, WANG Ru-zhu*1, EIKEVIK Trygve Magne2
(1-Institute of Refrigeration and Cryogenics, Shanghai Jiao Tong University (SJTU), Shanghai 200240, China; 2-Norwegian University of Science and Technology (NTNU), KolbjornHejesvei 1B, Trondheim, NO-7491, Norway)

Based on the existing mathematical model of mass entrainment ratio, a hybrid model for single phase R744 ejector system was developed. Firstly, based on the fluid dynamics and heat transfer theory, a theoretical model of mass entrainment ratio was established, and then it was simplified by considering the fluid status at the ejector inlet and outlet. The obtained new mathematical model contains five unknown parameters, and the fitting method for the parameters is also given. The comparisons of the calculation and experimental results indicate that the new model has a higher accuracy.

Ejector; Mass entrainment ratio; Mathematical model; R744

10.3969/j.issn.2095-4468.2015.02.101

*王如竹（1964-），男，教授。研究方向：制冷与低温技术。联系地址：上海市闵行区东川路800号，邮编：200240。联系电话：15800967634。E-mail：rzwang@sjtu.edu.cn。