增强型轨道列表星历及其在北斗混合星座中的应用
2015-12-15张中凯周佩元
路 余,杜 兰,张中凯,周佩元
(信息工程大学导航与空天目标工程学院,郑州450001)
0 引言
我国自主发展的北斗卫星导航系统已于2012年底实现了亚太地区的区域导航定位服务[1]。导航星座由中高度圆轨道(MEO)、倾斜地球同步轨道(IGSO)和地球静止轨道(GEO)三类卫星组成。卫星的广播星历提供了导航服务的空间基准,因此是影响卫星导航定位精度和可靠性的重要因素。目前广播星历参数有两大类,一是基于轨道根数的GPS型广播星历[2],另一类是基于卫星状态向量的GLONASS型广播星历[3]。后者由于模型参数少,参数的有效期较短,因而更新更加频繁。
北斗混合星座的广播星历采用类似于GPS的标准广播星历格式,其中GEO卫星采用了5度倾角旋转法以避免轨道根数的奇点问题[4]。但是,用户计算GEO卫星位置还需要反向旋转以恢复正确的轨道定向[5]。如此以来,破坏了用户使用北斗混合星座广播星历的算法一致性。
本文提出了一种增强型轨道列表星历参数模型。首先,仍采用基于卫星状态向量的参数表示法,保留了GLONASS型广播星历的无奇点特性;其次,改进了卫星的摄动力模型,星历有效期从原来的30分钟扩展到数小时,同时星历参数也从原来的9个增加为15个。与目前采用的GPS型广播星历相比,新模型的参数个数、参数有效期和更新频率均保持一致,且能够同时适用于MEO、IGSO、GEO三类卫星轨道的短期运动特性描述,无需对GEO卫星进行人为旋转。对北斗混合星座的星历参数拟合实验表明,三类卫星的2小时拟合精度在非地影期均优于1 cm。
1 GLONASS标准广播星历模型
GLONASS型广播星历是通过对地心地固坐标系(ECEF)下的力模型进行数值积分来计算卫星位置的[6]。由于星历更新较快,所需的轨道外推时间短,摄动力仅考虑了对轨道影响较大的摄动主项。
令卫星的状态向量为ECEF下的位置和速度向量,即XT=[RT˙RT],则状态微分方程为

式中:牛顿加速度主项a0、aJ2和a3b分别为ECEF下的地球中心引力加速度、地球扁率摄动加速度和日月引力摄动加速度向量;随后的两项是由于在非惯性系下描述二阶时间导数而引进的牵连加速度主项,分别为离心加速度和科里奥利加速度向量,其中示平均地球自转角速度。
1. 1 9参数星历模型
在GLONASS标准广播星历模型中,由于广播星历作用时间短(每30分钟更新),日月引力摄动加速度a3b不再用其具体力模型计算,而是简单地令其在有效期内保持为待求解的常向量。此时,扩展的9参数状态向量为XT=[RT˙RTaT3b],且带有初值条件的扩展状态微分方程为

若已知历元t0时的星历参数X0,利用积分器进行数值积分,即可得到有效期内任意时刻的ECEF下的卫星位置和速度向量。为了和GLONASS星历拟合方法一致,文中同样采用的是Runge-Kutta四阶积分器,文献[7]分析了积分器误差对GLONASS广播星历拟合的影响,可以通过缩短积分步长提高拟合精度。
1. 2 星历拟合误差
由拟合时段内精密外推轨道的位置向量序列[Ri](i=1,2,…n),通过最小二乘平差方法可以拟合出式(2)中的星历参数X0的最佳估值。具体解算流程与轨道确定相同,参见文献[8]。
采用GLONASS标准9参数星历模型,对北斗混合星座的三类卫星进行了星历拟合仿真实验。拟合数据[Ri]由复杂力模型和 Runge-Kutta7(8)阶积分器计算得到,并作为轨道位置真值。拟合时段分别为30分钟和1小时,数据间隔均取300秒。拟合参数的初值设定中,位置速度向量取为历元时刻t0外推值,日月引力摄动加速度a3b取为零向量。
对北斗星座的14颗卫星进行了大量拟合实验,图1给出了三类卫星的一组典型的拟合误差分布图。可以看出:
(1)标准30分钟拟合条件下,三类轨道都能达到2 cm的拟合精度,说明GLONASS的9参数模型可以直接用于北斗星座中高轨卫星的30分钟超短期星历。
(2)当扩展到1小时时段的星历拟合时,位置三分量的拟合误差迅速增大了一个数量级(达到0.2 m),远远超出拟合精度要求。
显然,对于数小时拟合时段,由于考虑的力模型过于简单,拟合误差还将进一步增加。此时,改进力模型将是有效方法。

图1 M2/G4/I2卫星30 min和1 h的拟合误差Fig.1 Fitting errors of M2/G4/I2 satellites for 30 min and 1 h
2 增强型轨道列表星历模型
目前北斗卫星广播星历的有效期为2小时,为此首先分析了日月引力摄动和太阳光压摄动在数小时内的变化特性,并据此建立了针对日月引力摄动的二次多项式逼近模型,从而提出了适用期更长的15参数星历模型。
2. 1 日月引力摄动及太阳光压摄动
日月引力摄动和光压是中高轨卫星的两个主要摄动力。通常力模型是在地心惯性系(ECI)中建立,因此考察两者在地心地固坐标系下的短期波动特性,还需要逐点进行地球自转变换。
在地心惯性系下,日月引力摄动加速度为[9]:

式中:G为引力常数,Mi为摄动天体的质量,ri为摄动天体相对于地心的位置矢量,ri为摄动天体到地心的距离,Δi为卫星相对于摄动天体的位置矢量,Δi卫星到摄动天体的距离。
采用柱形地影模型的太阳光压标准模型为[10]:

式中:ν=0时卫星在地影期,ν=1时卫星在非地影期。P⊙为卫星所在区域的太阳辐射流量,CR为光压系数,A为卫星有效截面积,m为卫星质量,r⊙为太阳相对于地心位置,AU为一个天文单位,其值约为1.496×108km。
需要注意的是,卫星进出地影使得力模型出现阶跃。地影是指太阳位于地球卫星轨道面附近且日、地、卫星近似在一条直线上时,受地球遮挡,卫星不能受到太阳光线照射并感知太阳位置的现象[11]。地影会造成太阳光压的间断,而GEO、IGSO与MEO卫星在入地影频度、持续时间、最长日期变化等方面均有所不同,在地影期间卫星受到的影响程度也不同。其中,GEO轨道的地影每年出现两次,分别在春分日和秋分日附近,每次持续46天;在地影季期间,每天卫星进入地影的时段不同,春/秋分日最长,约为72分钟。
2. 2 实验分析
考察中高轨卫星的两摄动力的量级及其在ECEF坐标系中数小时内的变化特性。仿真时间选在春分日(3月21日),此时太阳位于赤道面,光压对GEO的摄动影响最大。令MEO和IGSO卫星轨道的赤道交点经度与GEO卫星定点经度相同,光压系数为 1.0,卫星的有效面质比为0.0003 m2/kg。
图2给出了非地影期的4 h内某MEO卫星的日月引力摄动、太阳光压摄动的加速度分量。首先,两种摄动力在30 min内变化较小,可以近似用平均值表示,但随着时间增加到2~4 h,用常值进行逼近的误差过大。其次,光压摄动的大小与星体参数即有效面质比成正比,且比日月引力摄动小2个数量级,可以忽略或由其它拟合参数吸收其影响,但是其造成的力模型间断在短时段内可能影响参数拟合精度。
对GEO和IGSO卫星的仿真有类似结论。因此,随着拟合时间的增加,太阳光压和日月摄动加速度可以采用多项式和(或)三角函数等进行数学逼近表示。
2. 3 15参数星历模型
为了控制星历参数的个数,在数小时的拟合时段内,选择采用二次多项式表示日月引力摄动加速度,即
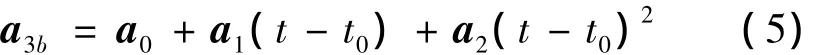
则有扩展的15参数状态向量为

且带有初值条件的扩展状态微分方程为

图2 MEO卫星的太阳光压(a)和日月摄动的短期波动变化(b)Fig.2 Acceleration change of the solar radiation pressure(a)and lunisolar gravitational perturbation for MEO satellite(b)
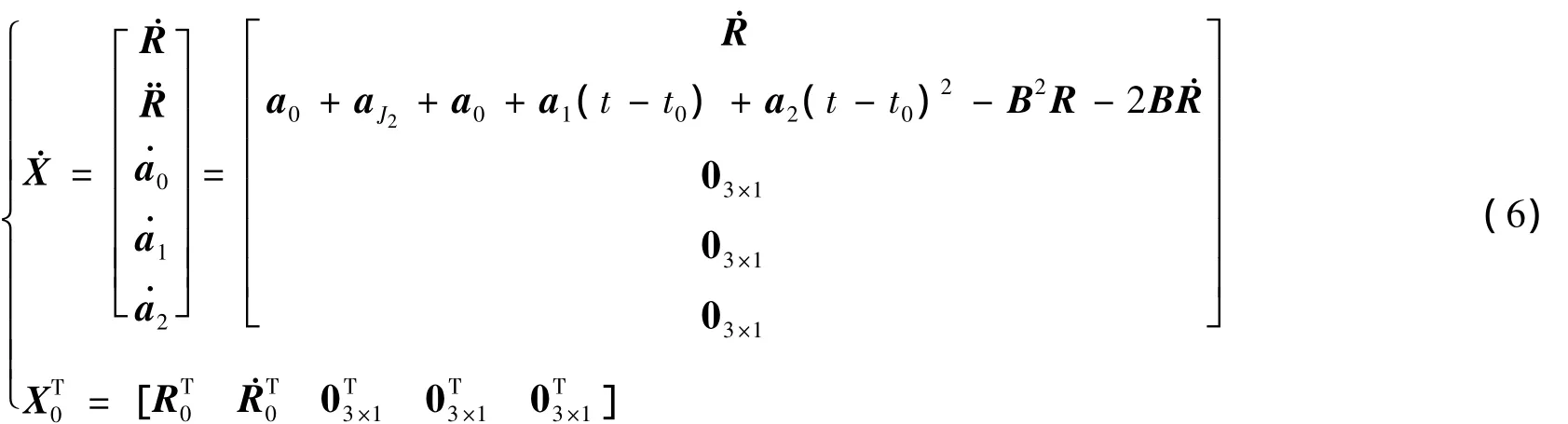
式中:参数初值X0的设定为[R0˙R0]取拟合时段中间点的位置和速度,力模型参数[a0a1a2]的初值全部取为零向量。
同理,若由拟合时段内精密外推轨道的位置向量序列[Ri],拟合出星历参数X0的最佳估值,则可用Runge-Kutta四阶积分器对式(6)积分得到有效期内任意时刻ECEF下的卫星位置和速度向量。
3 拟合实验和分析
将15参数的增强型轨道列表星历模型用于目前北斗混合星座中14颗卫星的星历拟合(5个GEO卫星G1~G5、5个IGSO卫星I1~I5和4个MEO卫星M1~M4)。首先分别对GEO/IGSO/MEO三类卫星在地心惯性系(ECI)下进行轨道外推,采用力模型包括15×15阶的地球引力场、日月引力摄动、太阳光压、海洋潮汐及地球固体潮汐等,并采用IERS发布的地球定向参数将外推轨道转换到ECEF坐标系下。仿真数据从2013年3月23日开始共计11天,数据点间隔为300 s;按照拟合时段和每小时更新频率进行分组,每颗卫星均包括264组星历拟合数据,历元时刻取为每组的中间时刻。需要指出的是,该实验时段内,5个GEO卫星均处于地影季,每天在地影内的时段在55~70分钟之间变动(见图3)。

图3 GEO的地影季和试验数据段的地影持续时间Fig.3 Daily variations of eclipse duration in the GEO satellite eclipse season centered around vernal equinox day
为考察15参数增强型轨道列表星历模型的适用性,拟合时段分别选取1/2/3/4 h进行实验。参数解算采用最小二乘平差,迭代终止条件为迭代前后两次单位权方差的相对变化小于0.001。参数初值中,位置和速度向量取拟合时段中间时刻的卫星位置和速度,其它参数均设为0;采用Runge-Kutta四阶积分器,分别向前和向后数值积分。
星历拟合的拟合精度采用用户距离误差(URE)的统计值进行评判[12]。MEO卫星的 URE计算公式:

式中:ΔR、ΔT和ΔN分别为卫星径向、沿迹和外法向位置分量的拟合误差。需要注意的是,这里仅分析星历参数的数学拟合精度,不包含轨道的外推误差。
图4为14颗卫星1/2/3/4 h的拟合URE的RMS最大值,初步表明增强型轨道列表星历模型设计能够满足1~3 h内北斗混合星座的广播星历参数拟合。
(1)在非地影期(左图),三类卫星的星历拟合误差随拟合时段的增加逐渐增大。拟合URE的RMS,在1~2 h拟合时段内优于1 cm,3 h拟合时段优于5 cm,但是4 h拟合的最大RMS已接近0.2 m。
(2)对比三类卫星可以看出,IGSO卫星的拟合误差最小,GEO卫星的拟合误差次之,MEO卫星的拟合误差最大。可能由于在地固系下,MEO卫星的轨道较低,其速度变化较快,拟合精度较差。
(3)在地影期(右图),5个GEO卫星广播星历的在2 h拟合时段内的 URE的 RMS最大值为1 cm,3 h拟合时段达到8 cm,4 h拟合时段的不能满足拟合要求。

图4 14个卫星拟合URE的RMS的最大值Fig.4 Max RMSvalue of 14 satellites fitting URE
图5 是G4卫星分别采用1/2/3/4小时的拟合URE的RMS分布图。每当卫星进出地影时,太阳光压导致卫星受力模型出现跳变,影响到外推轨道的局部平滑性[13],进而导致星历拟合的较大误差。由于每天的地影期持续1小时左右,因此仅能影响其附近的几组数据,导致拟合误差分群,跳变间隔约为1天,图中共有5组跳变现象(注意到,图5中左上1 h拟合时,若地影数据本身恰好组成一组,则不影响拟合精度,因此图中的跳变并非1天)。此外,随着拟合时段的增加,受地影数据影响的比例逐渐减小,拟合精度趋于平稳,但是拟合精度自身随时段延长衰减更快。因此,控制地影对星历拟合的影响,应在地影期间适当缩短拟合时段。
图6给出了G4星分别利用1/2/3/4 h拟合的星历参数积分计算的ECEF速度精度。随着拟合时长的增加,R和T方向的速度误差快速增大,且幅度较为一致,N方向速度误差最小,且对拟合时长不敏感。其中,2 h拟合结果计算的卫星速度在R、T、N方向的误差均优于0.005 mm/s,即使在地影期也能控制在 0.05 mm/s。
4 结束语
本文分析了北斗混合星座的中高轨卫星在数小时内的摄动运动变化特性,提出了基于扩展状态向量的15参数增强型轨道列表星历模型。通过对GEO、IGSO、MEO三类卫星的星历拟合实验表明,增强型广播星历能够满足1~3 h拟合时段的拟合URE精度要求。与现有的基于轨道根数的GPS型星历模型相比,避免了奇点问题,数值积分可方便地同时得到卫星位置和速度信息,因此可考虑在广播星历或者星基增强系统中采用和备份发播。
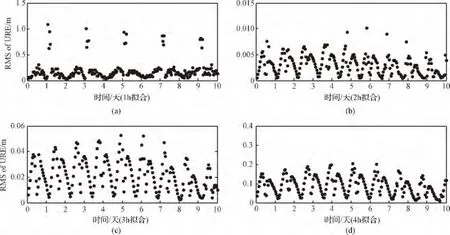
图5 G4卫星拟合URE的RMS分布Fig.5 RMSdistribution of the G4 satellite fitting URE
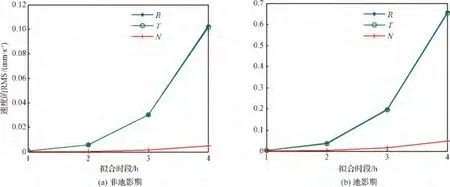
图6 G4卫星速度拟合误差RMSFig.6 RMSerrors of the G4 satellite fitting velocity
[1] Shi C,Zhao Q L,Li M,et al.Precise orbit determination of Beidou satellites with precise positioning[J].Sci China Earth Sci,2012,55(7):1079 -1086.
[2] 崔先强,焦文海,贾小林,等.GPS广播星历参数拟合算法[J].测绘学院学报,2004,21(4):244-246.[Cui Xianqiang,Jiao Wen-hai,Jia Xiao-lin,et al.The fitting algorithm of GPSbroadcast ephemeris parameters[J].Journal of Institute of Surveying and Mapping,2004,21(4):244 -246.]
[3] 郭际明,孟祥广,李宗华,等.GLONASS卫星广播星历精度分析[J].大地测量与地球动力学,2011,31(1):68-71.[Guo Ji-ming,Meng Xiang-guang,Li Zong-hua,et al.Accuracy analysis of GLONASSsatellites broadcast ephemeris[J].Journal of Geodesy and Geodynamics,2011,31(1):68 -71.]
[4] 何峰,王刚,刘利,等.地球静止轨道卫星广播星历参数拟合与试验分析[J].测绘学报,2011,40(增刊):52-58.[He Feng,Wang Gang,Liu Li,et al.The ephemeris fitting and experiments analysis of GEO satellite[J].Acta Geodaetica et Cartographica Sinica,2011,40(Supplement):52 -58.]
[5] 崔先强,杨元喜,吴显兵.轨道面旋转角对GEO卫星广播星历参数拟合的影响[J].宇航学报,2012,33(5):590-596.[Cui Xian-qiang,Yang Yuan-xi,Wu Xian-bing.Influence of the orbital plane rotation angle on GEO satellite broadcast ephemeris parameter fitting[J].Journal of Astronautics,2012,33(5):590 -596.]
[6] 葛奎,王解先.GLONASS卫星位置计算与程序实现[J].测绘与空间地理信息,2009,32(2):19-22.[Ge Kui,Wang Jie-xian.Calculation of GLONASS satellite station and the realization of program[J].Geomatics& Spatial Information Technology,2009,32(2):19 -22.]
[7] 贾小林,焦文海,吴显兵.GLONASS广播星历用户算法精度分析[J].测绘学院学报,2005,22(3):160-162.[Jia Xiaolin,Jiao Wen-hai,Wu Xian-bing.The accuracy analysis of the user arithmetic GLONASS broadcast ephemeris[J].Journal of Institute of Surveying and Mapping,2005,22(3):160 -162.]
[8] 杜兰.GEO卫星精密定轨技术研究[D].郑州:信息工程大学,2006.[Du Lan.Research on GEO satellite precision orbit determination[D]. Zhengzhou:Information Engineering University,2006.]
[9] 李济生.人造卫星精密轨道确定[M].北京:解放军出版社,1995.
[10] Montenbruck O,Gill E.Satellite orbits:models,methods and applications[M].Berlin:Springer,2000.
[11] 张中凯,杜兰,王若璞,等.混合星座卫星轨道阴影期分析[C].第四届中国卫星导航学术年会,武汉,2013年5月15- 17 日.[Zhang Zhong-kai,Du Lan,Wang Ruo-pu,et al.Analysis on eclipses of satellite orbits in mixed constellation[C].China Satellite Navigation Conference,Wuhan,May 15 - 17,2013.]
[12] Zhou S S, Cao Y L,Zhou J H,et al.Positioning accuracy assessment for the4GEO/5IGSO/2MEOconstellation of Compass[J].Science China Physics,Mechanics and Astronomy,2012,55(12):2290-2299.
[13] 杜兰,张中凯,刘利,等.GEO卫星广播星历的拟合参数设计[J].中国空间科学技术,2013,33(3):46-51.[Du Lan,Zhang Zhong-kai,Liu Li,et al.Fitting parameters design for GEO broadcast ephemeris[J].Chinese Space Science and Technology,2013,33(3):46 -51.]
[14] 谭述森.北斗卫星导航系统的发展与思考[J].宇航学报,2008,29(2):391 -396.[Tan Shu-sen.Development and thought of Compass navigation satellite system [J].Journal of Astronautics,2008,29(2):391 -396.]
[15] Mullins L D.Calculating satellite umbra/penumbra entry and exit positions and times[J].Journal of the Astronautical Sciences,1991,39(4):411-422.
[16] Zhou SS,Hu X G,Wu B,et al.Orbit determination and time synchronization for a GEO/IGSO satellite navigation constellation with regional tracking network [J].Science China Physics,Mechanics and Astronomy,2011,54(6):1089-1097.
