小波极大值方法及其在电磁异常信号提取中的应用

韩 冰 汤 吉* 赵国泽 毕亚新 王立凤 程远志

1)中国地震局地质研究所，地震动力学国家重点实验室，北京 100029

2)阿尔斯特大学，计算机与数学系，贝尔法斯特，BT370QB

0 引言

大量的观测事实说明，在地震之前会发生电磁场异常现象，如果能够说明这些异常现象与地壳内部的关系，就能够对地震作出预报。但是，关于电磁异常现象的有效提取和捕捉仍然是一个未解决的问题。这方面许多学者已经展开多方面的努力和研究，例如关于利用卫星技术观测空间电磁场的异常变化(卓贤军等，2005;汤吉等，2007;赵国泽等，2007;张蓓等，2010;刘君等，2011;张建国等，2013)，在地面利用自然电位(李树华等，2004)、地电阻率(徐光晶等，2009;高曙德等，2010，孙维怀等，2012)、地磁场、大地地电场(范莹莹等，2010)以及应用最新的人工源极低频技术(CSELF)等方法(赵国泽等，2003，2010;ZHAO et al.，2009;卓贤军等，2011)观测电磁异常现象。汶川MS8.0特大地震发生后，人们也对很多已观测到的电磁信号做了大量研究，汤吉等(2010)研究了强余震前武都台附近电、磁场同震变化现象;杜学彬等(2010)研究了主震前中期阶段的地电阻率变化;张蓓等(2010)观察到了DEMETER卫星记录到的电磁异常现象等。此外，赵国泽等(2009)基于该区深部电性结构研究了主震的孕震环境。这些观测与研究都说明，地震孕育和发生过程中，可能伴随着电磁场的扰动现象。

但是相对于丰富的观测数据，对电磁信号的处理方法仍显得相对简单和落后，台站观测和数据分析预报人员目前一般都是直接观察时间序列信号的变化来判定是否存在异常，或者经过简单的时频变换来观察一定时间段叠加的频谱来鉴别异常。在一定程度上，这种方法或许是直观、有效的，但是没能挖掘和利用数据中包含的大量信息，需要发展新的技术。如何识别异常，以及如何评价异常与地震等事件的关系，是长期困扰着我们，也是人们一直关注的研究课题。本文将应用小波极大值方法对这个问题进行探讨研究。

小波分析方法与应用数学、计算机科学、信号与信息处理、图像处理、地震勘探等多个学科有关。它具有在时间域、频率域等突出分析信号局部特征的能力(Mallat et al.，1992;程俊等，1995;熊攀，2009)。在对信号进行表示和描述中，可有效揭示信号的一些奇异点，如过零点、极值等，能刻画信号的细节和辨识不同类型的信号(Cervone et al.，2004，2005;陈顺云等，2006;Pan et al.，2009;熊攀等，2009;Bi et al.，2009)。

2013年4月20日8时2分，在四川雅安发生MS7.0地震，震中位于芦山县太平镇和双石镇之间，微观震中为30.28°N，102.99°E，震源深度16.33km，震中最大烈度达Ⅸ度。芦山地震是一次典型的主-余震型地震，至少发生了7次5～5.9级余震，30次4～4.9级余震;＜4级余震超过万次。余震沿发震断裂(双石-大川断裂)向主震两侧延伸，主要分布在长约32km、宽15～20km、深度为5～24km的范围内。地震破裂带向SW方向扩展范围较大，NE方向略小。为了观测研究震后电磁场变化与余震之间可能的关系，中国地震局地质研究所电磁组于5月2日赶往芦山县进行电磁观测，围绕主震震中区设置宝胜乡、芦山县双石镇、雅安市中里乡3个固定观测点进行连续观测。其中，宝胜测点位于主震震中的NE方向(N47°E)约9km处，经纬度为103°02'42.53″E，30°19'33.31″N(图1)。绝大部分余震沿着双石-大川断裂展布，宝胜观测点在余震区域的边缘处，它的位置既可以有效地监测到电磁信号可能的变化，又不会受到余震本身最直接的影响，对于观测是有利的。本文利用小波极大值方法，分析芦山地震震后宝胜观测点的电磁数据;利用连续小波变换方法，提取观测数据中不同频率电磁场的小波极大值，从极大值表现出的集中分布来识别可能与余震相关的电磁异常。

1 数据观测、处理及筛选

本次观测使用德国Metronix公司的ADU07大地电磁仪器，采用正SN-EW向的大地电磁测深布极方式进行观测，磁传感器为MFS-06e，电传感器为Pb-PbCl2不极化电极。测量的物理量为:磁场SN分量(Hx)、EW分量(Hy)和垂直地面分量(Hz);电场SN分量(Ex)，EW分量(Ey)。观测电场的SN和EW向电极距都为50m;后移动SN向电极的位置，电极距不变，而EW向电极距变为43m。本次监测记录时间为2013年5月4日0点至2013年6月11日12时整，记录方式为每4h为一个循环，每4h中XX:00:00—XX:10:00以4 096Hz采样率采集数据，XX:12:00-XX+3:58:00以128Hz的采样率采集数据，其中XX表示1d中循环观测的起始时间(00，04，08，12，16，20时)。采集得到的数据使用Metronix公司提供的Mapros软件进行处理，得出大地电磁测深响应的EDI文件，这样，每4h可得到1组视电阻率、阻抗相位和电磁场各分量功率谱的数据，然后观察不同频率的视电阻率，电磁场随着时间的变化规律。

由于电磁信号本身比较微弱，且特别容易受到外界的干扰，为了得到可信的观测数据，在数据处理过程中对数据进行了严格的筛选。

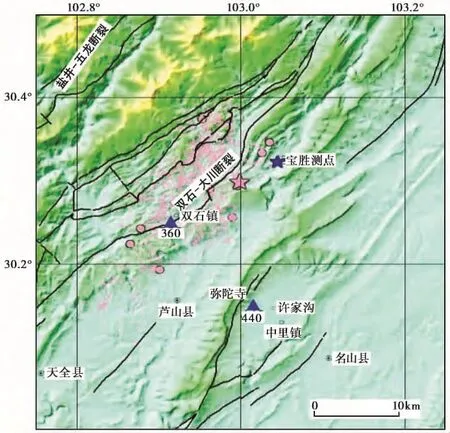
图1 芦山地震震区图Fig.1 The geologic-topographic map of the Lushan earthquake area.

(1)在mapros软件中，对原始时间序列中存在的脉冲，方波等干扰进行剔除。

(2)处理得到的视电阻率曲线尽量保持圆滑连续，由于每个循环的时间只有4h，对于低频来讲观测时间短，所以对得到的低频视电阻率不平滑连续的予以剔除。

(3)在得到各个时间段的视电阻率曲线以后，把得到的所有视电阻率曲线叠加在一起，观察视电阻率曲线的数据变化趋势，对于偏离整体趋势较大的曲线进一步处理观察，确认其是由干扰引起的变动还是由电磁场的本身变化引起。

图2为最终得到的137条视电阻率叠加图。由图2可以看出，视电阻率曲线整体上比较平滑，形态合理。但＜0.1Hz频率的数据由于记录时间短波动较大，所以把关注点放在0.1～1Hz范围内。

2 小波极大值基本原理

2.1 小波变换

对信号进行分析，最常用的方法就是傅里叶变换，它能揭示信号在频率域的特点，但其本身仍然存在缺陷，即不能提供信号在时域上的特征。如图3所示，由3个持续时间相同、频率和出现的次序不同的正弦波所组成的2组信号，当对这2组信号进行傅里叶变换后，发现它们频谱的分布和幅度是完全一致的，虽然可以分辨出信号中的3个基本频率，但是从傅里叶变换的频谱中却无法分辨这3个正弦波所发生的先后次序。为了能够同时表示函数在时间域和频率域的特征，在傅里叶变换基础上提出了短时傅里叶变换，即给信号加上1个窗口然后再进行傅里叶变换，但是因为有限的窗口长度使其频率分辨率和时间分辨率都受到限制，只是一种折衷的解决办法。小波变换的思想就是建立在可自动调节长度的视窗函数之上，它精确地揭示了信号在时间和频率方面的分布特点，可以同时分析信号在时域和频域中的特征，并可用多种分辨率来分析信号(Ingrid，1992)。

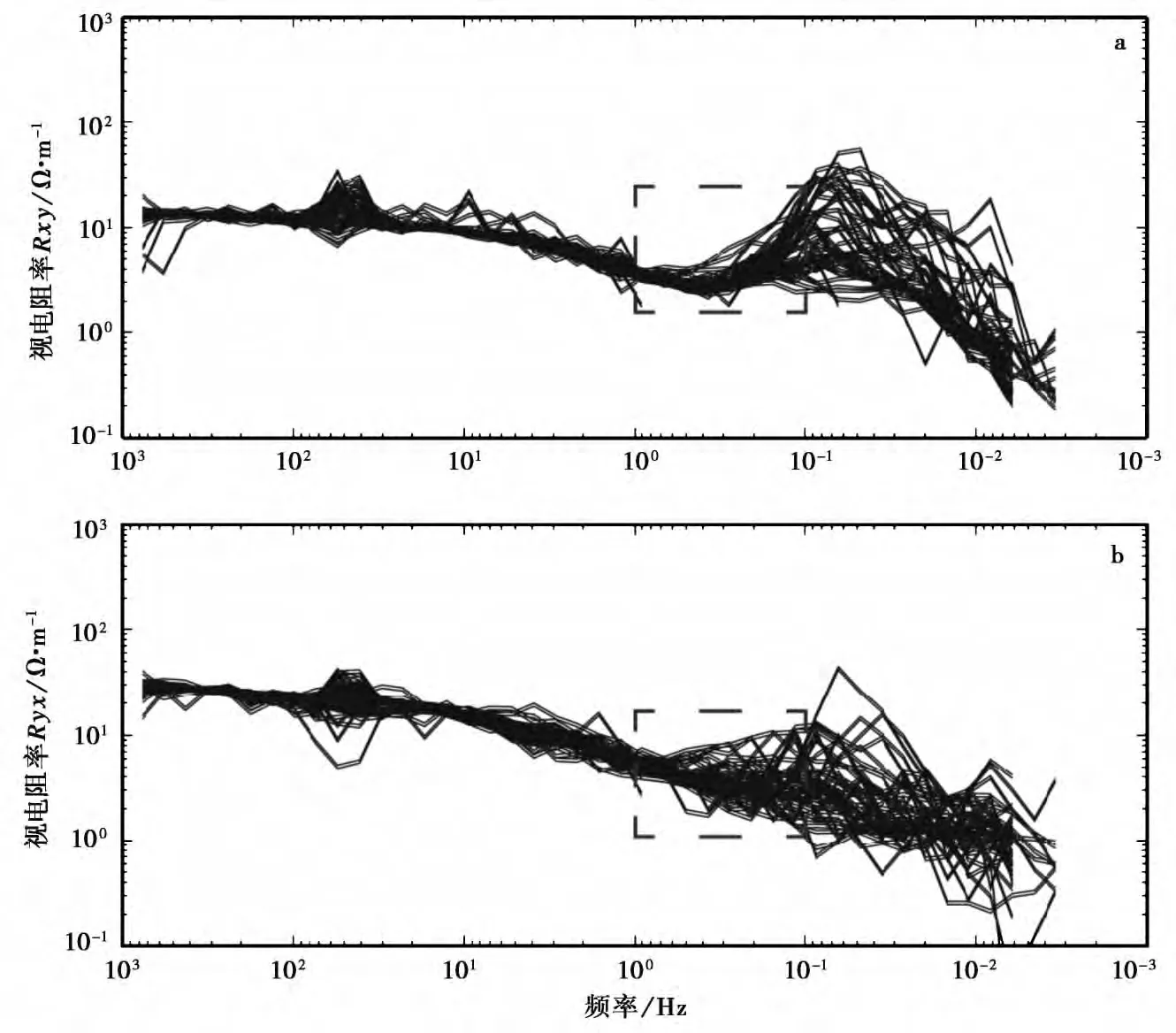
图2 宝胜乡5月4日至6月11日视电阻率曲线图Fig.2 Superposition of apparent resistivity curves of Baosheng station from May 4 to June 11.a Rxy;b Ryx

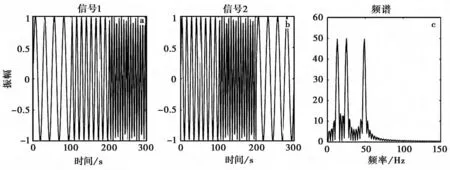
图3 2组具有不同时序的不稳定信号(a和b)和它们所对应的相同的频率谱(c)Fig.3 Two different unstable signals(a and b)and their frequency spectrum(c).

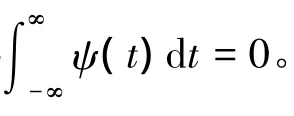
对比图3中的信号傅里叶分析结果，图4给出了相同信号小波变换的结果——小波系数图。小波系数图在时-频域对信号进行表达，其中横轴为时间，纵轴为尺度(与频率相关)，由图4可以看出:1)信号频率与尺度的对应关系，低频对应大尺度，高频对应小尺度;2)小波变换系数给出了信号的时间细节信息。即在什么时刻小波信号主要处于什么频段小波系数都可以给出;3)小波极大值对应正弦波信号的拐点，即图中小波系数最亮的中间位置，对应的都是信号的拐点;4)小波系数在信号发生变化的时间点处，小波系数在细尺度上收敛于这个奇异点，即在点(100，200)处小波系数在细尺度上取得极大值。

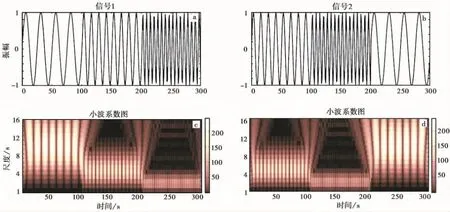
图4 原始信号及其小波系数图Fig.4 The signals and their wavelet coefficient.

2.2 小波极大值——确定异常发生的位置

对信号进行小波变换后得到时间-尺度的小波系数，对于任一尺度s0，小波系数模|Ws0f(t)|即为一条随着时间t变化的曲线，小波极大值|Ws0f(t0)|就是该曲线的极大值，定义如下:

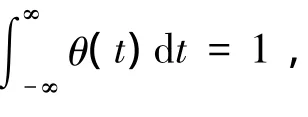
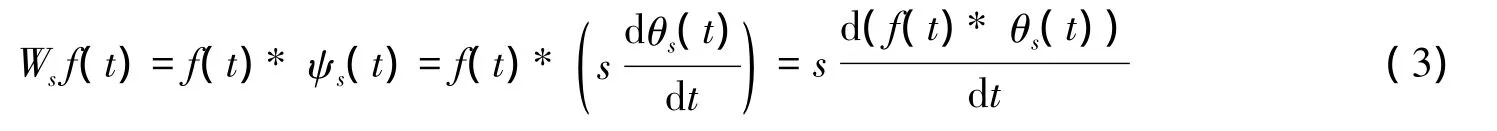
即小波变换Wsf(t)可表示成信号f(t)在尺度s被θs(t)平滑后的一阶导数。小波变换Wsf(t)幅值极大点对应着f(t)的突变点，这就是小波变换用于信号异常提取的基本原理。

小波极大值给出异常出现位置的信息，而且可以证明极大值曲线在小尺度上收敛于异常发生的位置(Mallat et al.，1992)。但极大值曲线有时在无法延伸到最小阶数之前便会中断，这是利用极大值曲线检测信号异常存在的一个问题，但如果选取小波函数为高斯函数的导数，那么所有的极大值曲线都可以延伸到最小的阶数(Yuille et al.，1986)。因此，本文进行小波变换选取的小波函数为guas3小波，另外尝试使用各种小波阶数进行实验，发现选择小波阶数为16时适用于本文所研究的信号。

如图5a所示，在光滑正弦信号f(t)=sin(0.1t+1)，t∈［1，300］中设置3个尖峰异常。使用小波极大值方法对模拟信号进行处理。首先对该信号进行小波变换得到小波系数谱图如图5b。其中横轴表示时间，纵轴表示尺度，颜色表示小波系数绝对值的大小。从图5可以看出，因为原信号频率较低，小波值在大尺度(表示低频)取值更大，而且在没有尖峰干扰的部分小波系数分布规律，这与信号本身的性质有关。在t=126，194，248点附近，小波系数的规律性变换被打乱，而且可以观察到在t=126，194，248的小尺度上，即s趋向于1时，小波变换系数出现了亮点，即此时的小波极大值系数很大。说明在小尺度下，小波系数在异常点处，会是该尺度下的极大值。

按照上述方法求取f(t)的小波系数极大值曲线(图5c)，把得到的连续小波极大值曲线显示于时间-尺度图中，发现极大值的分布存在8条极大值曲线(从左到右编号分别为1—8)，其中第1条是受小波变换的边界效应影响，暂不予以考虑。另外7条在小尺度分别汇聚于t=53，85，126，194，248，273等6个点处。

先讨论t=126，194，248处的4条极大值曲线(线4，5，6，7)。在t=194处出现了2条极大值曲线，但是在细尺度下这些模拟极大值曲线收敛点的坐标就是奇异发生的时刻。且在小波系数谱中可以看出，添加奇异点的3个位置在小波系数最小尺度处都出现了明显的极大值(如图5b)

此外，如图5c中t=53，85，273处(第2，3，8极大值曲线)处原始时间序列光滑没有奇异点。而且3条极大值曲线直观上看为直线，而且对应的为正弦曲线拐点出现的位置，这是因为正弦曲线拐点是信号变化最大的位置，此处出现极大值曲线在理论上是合理的，但是此处并没有放置异常点，小波系数值(图5b)在细尺度下也没有出现极大值。在下一步Lipschitz的计算中继续讨论这3条极大值曲线，观察信号这3个点存在奇异性。

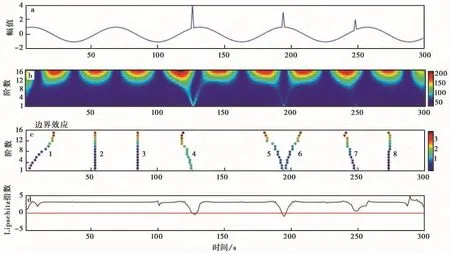
图5 模拟信号及其小波变换，小波极大值及Lipschitz指数α图Fig.5 Simulated signal and its wavelet transformation coefficients，wavelet maxima and Lipschitz exponentα.

2.3 Lipschitz指数——度量信号奇异性

通常情况下，信号奇异性分2种情况:一种是信号在某一时刻，其幅值发生突变，引起信号的非连续，幅值突变处称为第1类间断点;另一种是信号外观上很光滑，幅值没有突变，但是信号的一阶导数有突变发生，一阶导数不连续，称为第2种类型的间断点。在数学上，局部异常经常用Lipschitz指数α来衡量。如1个函数f在t0点不可微，则说它在t0点是奇异的。利用小波变换可以进一步求取信号的Lipschitz指数α。

Lipschitz指数α定义如下:对函数f(t)，如果存在1个常数C，以及m=⎿α」阶多项式P(t)使得

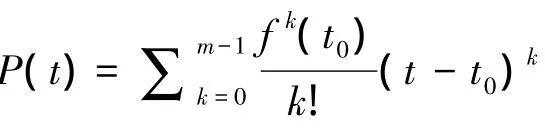
为了使用小波方法求得Lipschitz指数，在进行小波变换时使用消失距为m的小波对公式(4)两边做小波变换，就可以消除这一项。得到

对式(5)两边求log，省略常数log(C)，可以得到

按照以上方法求取模拟信号的Lipschitz指数α，其结果如图5d所示，在出现小波极大值的t=148，242，274处Lipschitz指数α＞1，且没有出现极小值等情况，说明这3个点处信号是光滑连续的，这3点并不能当做是奇异点。而在t=126，194，248附近可以观察到Lipschitz指数α＜1，且已经接近于0;说明该时间信号奇异性很强，由奇异值的大小也可以进一步判定出t=126，149，248处的异常强度依次减弱。

3 小波极大值方法在电磁信号异常提取中的应用

3.1 分析思路

把小波极大值方法应用于芦山地震后观测的电磁场数据中，以观测到的视电阻率曲线和阻抗相位曲线的光滑度作为评价数据质量的依据，选择其中数据质量较好的频段作为本文分析的重点，所分析的频段范围为 0.1～1Hz，对其中 0.207Hz，0.278Hz，0.373Hz，0.5Hz，0.671Hz，0.9Hz 6个频点的数据进行分析，研究电磁场的变化。由于观测过程中电极位置发生了变化，因此本文只分析磁场Hx(SN向)、Hy(EW向)和Hz(垂直)的观测数据。经过前期处理，得到了3个磁场分量在6个频点的自功率谱随着时间变化的曲线，对每条曲线求取小波极大值和Lipschitz指数α，并把同一磁场分量的6个不同频点的小波极大值结果进行比较，观察其随时间的变化规律，并结合Lipschitz指数α值的大小来判断出现的极大值是否为异常点。

根据芦山地震余震目录，将地震区内在电磁场观测数据的每4h内发生的所有余震换算为本区的地震能量，其能量换算按照式(7)。

式(7)中:Mi表示4h内发生的第i个地震，n表示4h内发生的地震总数。计算得到震级M对应的地震能量，按照电磁场记录方式以4h为1个时段，计算每个时段的地震总能量，最后得到1条随着时间变化的地震能量曲线图，同样用小波极大值方法分析这些曲线(图6—8)，把得到的结果与磁场变化的小波极大值进行对比分析(图6—8)。其中图6—8分别为3个磁场分量小波极大值分布图，颜色由蓝色到红色表示小波极大值由小到大，使用guas3小波，求取16阶小波系数。图9为3个磁场分量Lipschitz指数α图，其中红色横线处Lipschitz指数α为零。

3.2 结果与讨论

本文结合6个频率3个磁场自功率谱随时间变化的小波极大值的分布规律以及它们的Lipschitz指数α的大小，对比相应的地震释放能量的变化，可以发现地震能量变化和磁场突变存在时间上的对应性，这些磁场的异常(突变)可能与地震相关(图5—8)。根据小波极大值和Lipschitz指数α的特点，给出异常判定标准如下:

(1)以Lipschitz指数α≤0，且是局部极小值或出现急剧减小变化为标准，来判定小波极大值曲线是否为信号异常点;

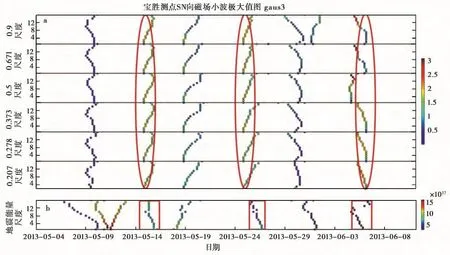
图6 SN向磁场及地震能量小波极大值分布图Fig.6 Wavelet maxima of the N-S magnetic field data(Hx)in Baosheng Station.

图7 EW向磁场及地震能量小波极大值分布图Fig.7 Wavelet maxima of the E-W magnetic field data(Hy)in Baosheng Station.

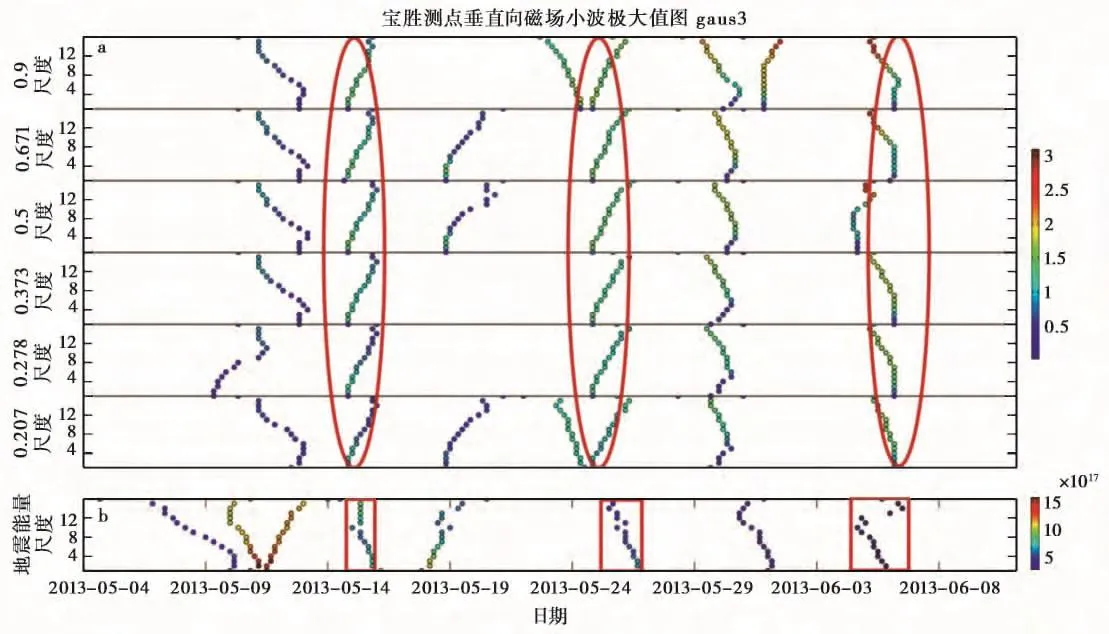
图8 垂直向磁场及地震能量小波极大值分布图Fig.8 Wavelet maxima of the vertical magnetic field data(Hz)in Baosheng station.

(2)单一分量中小波极大值线在3个及3个以上频率上都出现;

(3)异常在3个磁场分量上都出现。

综合以上标准得到3个可能与地震相关的磁场异常，如图5—7所示由椭圆圈出。其中第1个和第2个异常后约12h有对应的地震能量发生相应的变化，如图中矩形所标出的部分。第3个异常前约4h地震能量有1个较小的异常变化，也如图中矩形所标出。看其他极大值的分布，尤其是Hx(图6a)中还有另外2条连续性非常好的极大值曲线，它们对应的Lipschitz指数α在相应的时间上也表现出代表奇异性强的小值，但是这种异常信息只在单个分量上有所体现，不把这些极大值线当成可能与地震相关的电磁异常发生的位置。其他极大值曲线并没有在不同的频率上表现出很好的连续性，这表明可能是某个频率在这个时间出现了一些干扰扰动造成的，这种扰动并不能在造成电磁场在各个分量和整个频段上的同时变化。另外，在5月30日左右在3个分量上都出现小波极大值，且在磁场异常后有地震能量的一个相应的变化，Lipschitz指数α也在一些频率上＜0，但是Lipschitz指数α表示的信号的奇异性不强，所以此处暂不定义为可能与地震相关的磁场异常。

对比分析3组异常，第1组异常(5月15日出现的磁异常)和第2组异常(5月25日出现的磁异常)磁场3个分量在不同频率上的小波极大值都表现出非常好的连续性，对应的Lipschitz指数α表现出1个负尖峰极小值，这说明在此刻电磁场出现了强的异常变化，这个变化影响了磁场3个分量的很宽的频段。另外细看单个磁场分量的极大值曲线，随着小波尺度变化，极大值大小也发生变化，整体上随着尺度的增大，小波极大值点值在变小，这也就说明了异常值在低阶小波(即高频)表现明显，即前2个异常表现出来的是一个高频的类似于尖峰的异常变化。第3组异常(6月6日出现的磁异常)在不同频率上小波极大值曲线表现出的连续性不如前2个异常，它们在某些频点处没有出现小波极大值曲线，而且Lipschitz指数α值接近于0，且随着尺度的变大，小波极大值点的值是逐渐变大的，这是一个相对低频异常的表现，说明此处电磁场的变化不是急剧，而是相对缓和但是幅值很大的变化。

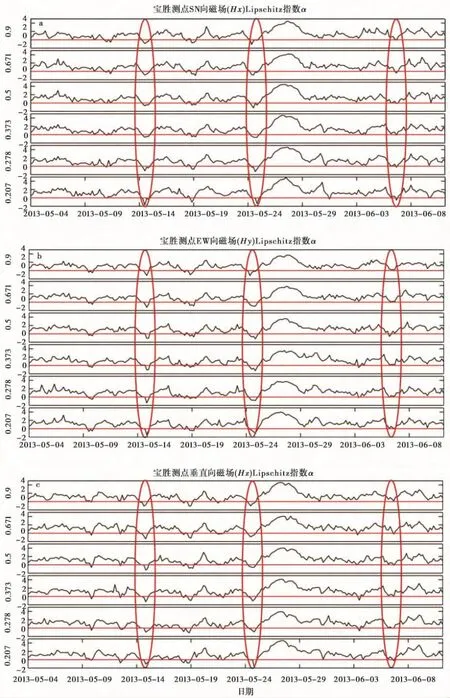
图9 SN向(a)、EW向(b)及垂向(c)磁场Lipschitz指数αFig.9 The Lipschitz exponentα of the SN magnetic field(a)，EW magnetic field(b)and the vertical magnetic field(c).

进一步对比1个分量上不同频率处异常大小的变化，可以发现在3组异常都表现出随着频率的升高极大值的大小有微弱的增加，即高频处极大值曲线的颜色相较于低频更暖。此现象在前2组异常表现不明显，但是在第3组异常处表现比较明显。这给出了异常变化与频率的1个关系，即高频电磁场的变化相对低频稍强。但是，这种变化规律在其他观测资料中是否存在并不能确定。

由小波极大值图可以找到电磁场异常出现的位置、大小等信息，但是与地震能量异常变化是否真的有对应关系，或者是怎么样的一种对应关系尚不能确定，即图中椭圆框出的异常与矩形异常是否有关系还需要进一步验证，但是小波极大值方法首先给我们一个找到信号异常的手段，也给我们一个全新的视角观察电磁信号的异常变化与地震能量信号异常变化的相互关系。

4 结论

本文把小波极大值法作为一种数据挖掘方法应用在电磁信号处理中，观测研究芦山地震震后电磁监测数据中可能与地震相关的电磁信号异常。首先利用小波极大值的分布确定异常发生的时间点;然后利用Lipschitz指数α来进一步判定异常的性质，给出电磁场异常变化的一些细节信息。最后结合地震能量异常分布来分析二者可能的相互关系。可以看出在地震能量变化之前或者之后1d内电磁场也会有异常现象出现。但是，在一些地震能量异常极大值出现周围并没有出现电磁场异常变化，而且震后余震发生密集，单个地震对电磁场的影响是不能完全区分开来的，因此电磁场异常变化与地震能量变化之间可能的相互关系还需要更长的电磁场记录与更多的震例来探索研究。